Дискретная математика для 1 курса. Тема Множества
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
ТЕМА 1. МНОЖЕСТВА1.1.Основные понятия Определение 1.1. Множеством называется совокупность каких-либо объектов, обладающим общим для всех характеристическим свойством. Это определение нельзя считать строгим, так как понятие множества является исходным понятием математики и не может быть определено через другие математические объекты. Один из основателей теории множеств Г. Кантор определял множество так: "Множество есть многое, мыслимое как целое". Пример 1.1. Следующие совокупности объектов являются множествами: множество деревьев в лесу, множество целых чисел, множество корней уравнения exsinx = 0.5. Всякое множество состоит из элементов. Множества обозначают большими буквами, например А. В, С, а элементы – маленькими буквами, например, а, b, c. Множество и его элементы обозначаются следующим образом: А = {a1, a2, a3} – множество, состоящее из трех элементов; А = {a1, a2, …} – множество, состоящее из бесконечного числа элементов. Множество может состоять из элементов, которые сами являются множествами. Нужно различать элемент a и множество, состоящее из единственного элемента a. Пример 1.2. Множество А = {1, 2} состоит из двух элементов 1, 2; но множество {А} состоит из одного элемента А. Если элемент a принадлежит множеству А, это записывается следующим образом: a А. Если элемент a непринадлежит множеству А, то записывают так: a А. Пример 1.3. Пусть А1 – множество простых чисел, А2 – множество целых чисел, a = 4. Тогда a А2, a А1. Если все элементы множества А являются элементами множества В и наоборот, т. е. множества А и В совпадают, то говорят, что А = В. Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В,и записывают А В или В А. Отметим, что по определению само множество А является своим подмножеством, т.е. А А. Если А В и В А, то по ранее введенному определению А = В. Если А В и А В, то А есть собственное подмножество В, А В. Если А не является собственным подмножеством В, то записывают А В. Пример 1.4. Пусть А – множество четных чисел, В – множество целых чисел, С –множество нечетных чисел. Тогда А В, С В, А С, В А. Не надо смешивать отношение принадлежности () и отношение включения (). Пример 1.5. Пусть А = {2} – множество, состоящее из одного элемента, В = {{2}, {4}} – множество, состоящее из двух элементов, каждое из которых является одноэлементным множеством. Тогда имеют место следующие соотношения: 2 {2}; {2} {{2}, {4}}; 2 {{2}, {4}}. Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается .  Принято считать, что пустое множество является подмножеством любого множества, А, где А – любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя. Принято считать, что пустое множество является подмножеством любого множества, А, где А – любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя.Пример 1.6. Множество корней уравнения sinx = 2 является пустым. Множество всех подмножеств данного множества А называется множеством-степенью и обозначается P(A). Множество P(A) состоит из 2n элементов (доказать самостоятельно). Пример 1.7. Пусть множество А = {1, 2} состоит из двух элементов 1, 2. Тогда множество P(A) включает в себя пустое множество , два одноэлементных множества {1} и {2} и само множество А = {1, 2}, т. е. P(A) = {, {1}, {2}, {1, 2}}. Мы видим, что множество P(A) состоит из четырех элементов (4 = 22). Существуют следующие способы задания множеств. 1. Перечислением элементов множества. Например: A = {1, 3, 5, 7, 9} – конечное множество; B = {1, 2, …, n, …} – бесконечное множество. 2. Указанием свойств элементов множества. Для этого способа пользуются следующим форматом записи: A = {aуказание свойства элементов}. Здесь a является элементом множества A, a А.Например: A = {a a – простое число} – множество простых чисел; B = {b b2 – 1 = 0, b – действительное число} – множество, состоящее из двух элементов, B = {– 1, 1}; Z = {x 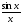 = 1}– множество, состоящее из одного числа, x = 0. = 1}– множество, состоящее из одного числа, x = 0.1.2. Операции над множествами Рассмотрим основные операции над множествами. Объединением множеств А и В называется множество АВ, все элементы которого являются элементами хотя бы одного из множеств А или В: АВ = {x x А или xВ}. Из определения следует, что А АВ и В АВ. Аналогично определяется объединение нескольких множеств Пример 1.8. а) Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда АВ = {2, 4, 5, 6}. б) Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда АВ множество чисел, которые делятся на 2 или на 3: АВ = {2, 3, 4, 6, 8, 9, 10, …}. Пересечением множеств А и В называется множество АВ, все элементы которого являются элементами обоих множеств А и В: АВ = {x x А и xВ}. Из определения следует, что АВ А, АВ В и АВ АВ. Аналогично определяется пересечение нескольких множеств. Пример 1.9. Рассмотрим данные из примера 1.8. а) Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда АВ = {4, 6}. б) Пусть А – множество чисел, которые делятся на 2, а В – множество чисел, которые делятся на 3: А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда АВ множество чисел, которые делятся и на 2 и на 3: АВ = {6, 12, 18, …}. Может оказаться, что множества не имеют ни одного общего элемента. Тогда говорят, что множества не пересекаются или что их пересечение – пустое множество. Пример 1.10. Пусть А = {1, 2}, В = {2, 3}, C = {3, 4}. Тогда АВC =. Относительным дополнением множества В до множества А называется множество А \ В, все элементы которого являются элементами множества А, но не являются элементами множества В: А \ В = {x x А и xВ}. Пример 1.11. Рассмотрим данные из примера 1.8. а) А = {4, 5, 6}, В = {2, 4, 6}. А \ В = {4, 5}, В \ А= {2}. б) А = {2, 4, 6, …}, В = {3, 6, 9, …}. Тогда А \ В – множество чисел, которые делятся на 2, но не делятся на 3, а В \ А – множество чисел, которые делятся на 3, но не делятся на 2: А \ В = {2, 4, 8, 10, 14, …}. В \ А= {3, 9, 15, 21, 27, …}. Симметрической разностью множеств А и В называется множество А + В: А + В = (А \ В) (В \ А). Пример 1.12. Рассмотрим данные из примера 1.11. а) А = {4, 5, 6}, В = {2, 4, 6}. А \ В = {4, 5}, В \ А= {2}, А + В = {2, 4, 5}. б) А = {2, 4, 6, …}, В = {3, 6, 9, …}, А \ В = {2, 4, 8, 10, 14, …}. В \ А= {3, 9, 15, 21, 27, …}, А + В = {2, 3, 4, 8, 9, …}. Универсальным множеством называется такое множество U, что все рассматриваемые в данной задаче множества являются его подмножествами. Абсолютным дополнением множества А называется множество 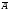 всех таких элементов x U, которые не принадлежат множеству А: всех таких элементов x U, которые не принадлежат множеству А: 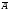 = U \ A. = U \ A.Пример 1.13. Пусть А – множество положительных четных чисел. Тогда U – множество всех натуральных чисел и 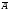 - множество положительных нечетных чисел. - множество положительных нечетных чисел.1.3. Геометрическое моделирование множеств. Диаграммы Венна Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна). Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга (рис 1.1а)). С помощью диаграмм Венна удобно иллюстрировать операции над множествами. 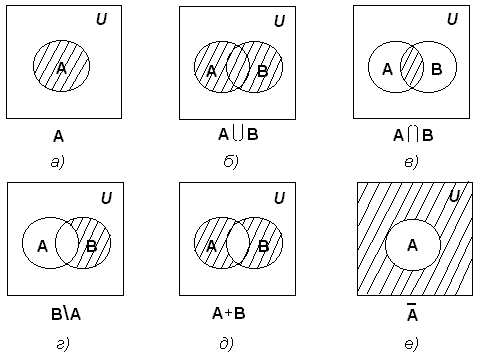 Рис.1.1 1.4. Алгебра множеств. Основные тождества алгебры множеств Множества вместе с определенными на них операциями образуют алгебру множеств. Последовательность выполнения операций задается с помощью формулы алгебры множеств. Например, 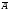 (ВC), (А \ В) + C – формулы алгебры множеств. (ВC), (А \ В) + C – формулы алгебры множеств.Основные тождества алгебры множеств Для любых множеств A, B, C справедливы следующие тождества: 1. Коммутативность. а) A B = B A (для объединения); б) A B = B A (для пересечения). 2. Ассоциативность. а) A (B C) = (A C) C (для объединения); б) A (B C) = (A B) C (для пересечения). 3. Дистрибутивность. а) A (BC) = (AB) (AC) (для объединения относительно пересечения); б) A(BC) = (AB)(AC) (для пересечения относительно объединения). 4. Закон де Моргана. а) 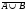 = = 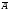  (дополнение к объединению есть пересечение дополнений); (дополнение к объединению есть пересечение дополнений);б) 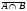 = = 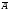  (дополнение к пересечению есть объединение дополнений). (дополнение к пересечению есть объединение дополнений).5. Идемпотентность. а) A A = A (для объединения); б) A A = A (для пересечения). 6. Поглощение. а) A (A B) = A; б) A (A B) = A. 7. Расщепление (склеивание). а) (A B) (A  ) = A; ) = A; б) (A B) (A  ) = A. ) = A.8. Двойное дополнение. 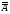 = A. = A.9. Закон исключенного третьего.  A 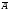 = U. = U. 10. Операции с пустым и универсальным множествами. а) A U = U; б) A = A; в) A U = A;  г) A = ; д) 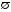 = U; = U;е) 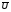 = . = .11. А \ В = A  . .Чтобы доказать некоторое тождество A = B, нужно доказать, что, во-первых, если x А, то xВ и, во-вторых, если xВ, то x А. Докажем таким образом, например, свойство дистрибутивности для объединения (тождество 3а)): A (BC) = (AB) (AC). 1. Сначала предположим, что некоторый элемент x принадлежит левой части тождества, т.е. x A (BC), и докажем, что x принадлежит правой части, т.е. x(AB) (AC). Действительно, пусть x A (BC). Тогда либо x A, либо x BC. Рассмотрим каждую из этих возможностей. Пусть x A. Тогда x A B и x A C (это верно для любых множеств B и C). Следовательно, x(AB) (AC). 2. Предположим, что некоторый элемент x принадлежит правой части тождества, т.е. x (AB) (AC), и докажем, что x принадлежит левой части, т.е. x A (BC) . Действительно, пусть x (AB) (AC). Тогда xAB, и одновременно x AC. Если x AB, то либо x A, либо x B, если .x AC, то либо x A, либо x C. Пусть x A, Тогда x A (BC) и утверждение доказано. Если x A, то одновременно должны выполняться условия x B и x C, т.е. x BC. Но тогда x BC и x A (BC), что также доказывает наше утверждение. Доказательство тождеств можно проиллюстрировать с помощью диаграмм Венна. Основные тождества алгебры множеств можно использовать для доказательства других тождеств. Пример 1.14. Доказать тождество (AB) \ В = A  . .Преобразуем левую часть тождества, используя тождество 11: (AB) \ В = (AB)  . .Затем используем закон дистрибутивности (тождество 3б): (AB)  = A = A  B B  . .Используем закон исключенного третьего (тождество 9): B  = . = .Получим A  B B  = A = A  . .Используем свойство пустого множества (тождество 10б): A  = A = A  . .Тождество доказано. Пример 1.15. Доказать тождество: A \ (В \C) = (A \ В) (AC). Множества, стоящие в левой и правой частях тождества, изобразим с помощью диаграмм Эйлера – Венна (рис. 1.2). 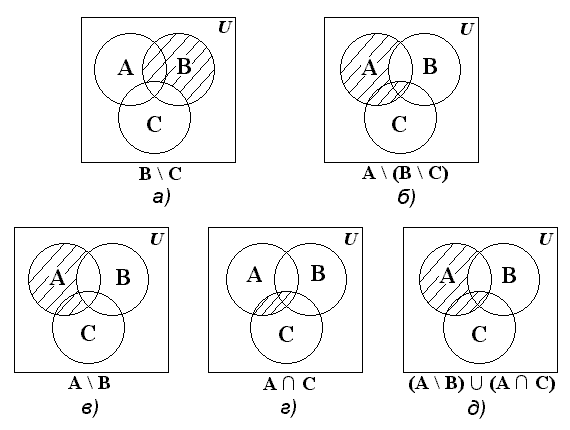 Рис. 1.2 Рис. 1.2б) и рис. 1.2д) иллюстрируют равенство множеств A \ (В \C) и (A \ В) (AC). Докажем тождество из нашего примера, воспользовавшись тождествами: А \ В = A  , , 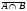 = = 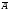  , , 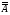 = A, A(BC) = (AB)(AC). = A, A(BC) = (AB)(AC).Получим: A \ (В\ C) = A 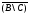 = A = A 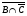 = A ( = A (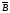 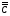 ) = A ( ) = A (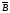 C) = (A C) = (A 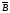 ) (A C) = (A \ В) (A C). ) (A C) = (A \ В) (A C).Основные тождества алгебры множеств можно также использовать для упрощения формул алгебры логики. Пример 1.16. Упростить выражение: (AB) ( 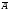 B) (A B) (A ). ).Используя закон коммутативности (тождество 1б), поменяем местами вторую и третью скобки: (AB) ( 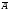 B) (A B) (A ) = (AB) (A ) = (AB) (A ) ( ) (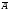 B). B).Применим закон расщепления (тождество 7а) для первой и второй скобок: (AB) (A  ) ( ) (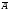 B) = A ( B) = A (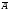 B). B).Воспользуемся законом дистрибутивности (тождество 3б): A ( 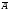 B) = A B) = A 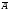 A B. A B.Используем закон исключенного третьего (тождество 9): A 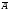 = . = .Получим A 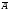 A B = A B. A B = A B.Используем свойство пустого множества (тождество 10б): A B = A B. Итак, (AB) (  B) (A B) (A ) = A B. ) = A B.1.5. Эквивалентность множеств Определение 1.2. Если каждому элементу множества A сопоставлен единственный элемент множества B и при этом всякий элемент множества B оказывается сопоставленным одному и только одному элементу множества A, то говорят, что между множествами A и B существует взаимно однозначное соответствие. Множества A и B в этом случае называют эквивалентными или равномощными. Эквивалентность множеств обозначается следующим образом: A B. Эквивалентность множеств обладает следующим свойством транзитивности. Если A B и B C, то A C. Докажем это свойство. Так как A B, то для всякого элемента a А существует единственный элемент b B. Но так как B C, то для всякого элемента b B существует единственный элемент c C. Сопоставим этот элемент элементу a А. Значит, для всякого элемента a А существует единственный элемент c C и для всякого элемента c C существует единственный элемент a А. Следовательно, A C. Очевидно, что два конечных множества эквивалентны тогда и только тогда, когда количество элементов в них одинаково. Например, множества А = {4, 5, 6} и В = {x, y, z} эквивалентны, A B. Взаимно однозначное соответствие может быть установлено между элементами 4 и x, 5 и y, 6 и z. Мощностью конечного множества А (обозначается А) называется число элементов этого множества. Например, мощность множества А = {1, 2} равна А= 2. Пример 1.17. Ранее (разд. 1.1) мы рассматривали множество всех подмножеств данного множества А, которое называется множеством-степенью и обозначается P(A). Множество P(A) состоит из 2n элементов. Таким образом, P(A) = 2n. Рассмотрим задачу определения мощности объединения n конечных множеств. Пусть n = 2 и A и B – два пересекающихся множества. Докажем с помощью диаграммы Эйлера – Венна следующее соотношение: АB = А + B – АB . (1.1) Из рис. 1.3 видим, что АB = n1+n2+n3; А = n1+n2; B = n2+n3; АB = n2. 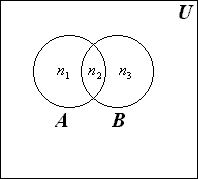 Рис. 1.3 Очевидно, что n1+n2+n3 = (n1+n2) +(n2+n3) – n2, что и доказывает формулу (). Формула (1.1) справедлива и для случая, если множества A и B не пересекаются. В этом случае АB = А + B . Пусть n = 3 и A, B и С – три пересекающихся множества. В этом случае справедливо следующее соотношение: АB С= А + B + C – АB – АC – BC + АB C . (1.2) Из рис. 1.4 видим, что АB С= n1+n2+n3+n4+n5+n6+n7; А = n1+n2+n4+n5; B = n2+n3+n5+n6; С=n4+n5+n6+n7; АB = n2+n5; АC = n4+n5; BC = n5+n6; АB C = n5. 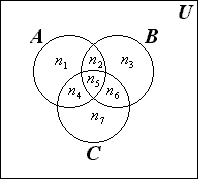 Рис. 1.4 Очевидно, что n1+n2+n3+n4+n5+n6+n7 =(n1+n2+n4+n5) + (n2+n3+n5+n6) +(n4+n5+n6+n7) – (n2+n5) – (n4+n5) – (n5+n6) + n5, что и доказывает формулу (1.2). Формула (1.2) справедлива и для случая, если множества A, B и С попарно не пересекаются. В этом случае АB С= А + B + C . В общем случае мощность объединения n множеств определяется по формуле: А1 А2 …Аn= А1+А2+…+ Аn– (А1 А2+ А1 А3+ … +Аn–1Аn)+ АB C + (А1 А2 А3 + … +Аn–2Аn–1Аn) – … + (–1)n – 1 А1А2 …Аn. (1.3) Эта формула выводится индукцией по n, [3]. Если множества Аi попарно не пересекаются, т.е. АiАj = , i j,то получим частный случай формулы (1.3): А1 А2 …Аn= А1+А2+…+ Аn. В общем случае справедливо неравенство А1 А2 …Аn А1+А2+…+ Аn. Понятие эквивалентности годится и для бесконечных множеств. Пусть, например, A = {1, 2, 3, …, n,…}, B = {– 1, –2, …, –n, …}. Тогда A B. Взаимно однозначное соответствие устанавливается по правилу: элементу n A соответствует элемент – n B, т.е. n – n. Пример 1.18. A = {1, 2, 3, …, n,…}, B = {2, 4 …, 2n, …}. Тогда A B. Взаимно однозначное соответствие устанавливается по правилу: n 2 n. Пример 1.19. A = {1, 2, 3, …, n,…} – множество натуральных чисел, B = {…, –n, …– 2, –1, 0, 1, 2, …, n, …} – множество всех целых чисел. Перепишем множество B следующим образом: B = {0, –1, 1, – 2, 2, …, –n, n, …}, так, что 0 будет на первом месте, –1 на втором, 1 на третьем, –2 на четвертом и т.д. Нетрудно заметить, что отрицательные числа будут стоять на местах с четными номерами, а 0 и положительные числа – на местах с нечетными номерами. Поэтому взаимно однозначное соответствие между множествами A и B устанавливается по правилу: для всякого n 0 элементу a = 2n +1 из множества A (т.е. нечетному элементу) соответствует элемент b = n из множества B; элементу a = 2n из множества A (т.е. четному элементу) соответствует элемент b = –n из множества B. Таким образом, реализуется взаимно однозначное соответствие между множествами A и B: 1 0, 2 –1, 3 1, 4 –2 и т.д. Примеры 1.18 и 1.19 показывают, что множество может быть эквивалентно своему подмножеству. Так, в примере 1.18 B A, а в примере 1.19 A B. И в том, и в другом случае A B. Установить эквивалентность множеств, т.е. установить взаимно однозначное соответствие между их элементами можно различными путями. На рис. 1.5 показано, что множества точек двух отрезков [a, b] и [c, d] эквивалентны. 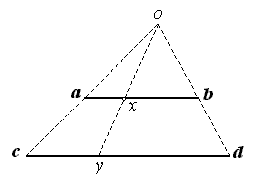 Рис.1.5 Таким же образом можно установить эквивалентность множеств точек двух интервалов. На рис.1.6 показано, что множества точек любого интервала (a, b) эквивалентно множеству точек всей прямой. 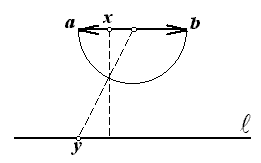 Рис. 1.6 Для установления эквивалентности двух множеств можно применять следующую теорему. Теорема Бернштейна. Если множество A эквивалентно части множества B, а множество B эквивалентно части множества A, то множества A и B эквивалентны. Применим теорему Бернштейна для доказательства того, что множество точек любого отрезка эквивалентно множеству точек любого интервала. Пусть A = [a, b] – произвольный отрезок, а B = (c, d) – произвольный интервал. Пусть A1 = [a1, b1] – любой внутренний интервал отрезка [a, b], A1 A. Тогда A1 B. Пусть B1 = (c1, d1) – любой внутренний отрезок интервала (c, d), B1 B. Тогда B1 A. Таким образом, выполняются условия теоремы Бернштейна. Поэтому A B. Итак, все интервалы, отрезки и вся прямая эквивалентны между собой. 1.6. Счетные множества Определение 1.3. Множество, эквивалентное множеству натуральных чисел N = {1, 2, 3, …, n,…}, называется счетным. Можно сказать также, что множество счетно, если его элементы можно перенумеровать. Пример 1.20. Следующие множества являются счетными.: 1. A1 = {–1, –2, …, – n, …}; 2. A2 = {2, 22, …, 2n,…}; 3. A3 = {2, 4, …, 2n,…}; 4. A4 = {…, – n, …, – 1, 0, 1, …, n,…}; Чтобы установить счетность некоторого множества, достаточно указать взаимно однозначное соответствие между элементами данного множества и множества натуральных чисел. Для примера 1.19 взаимно однозначное соответствие устанавливается по следующим правилам: для множества A1: –n n; для множества A2: 2n n; для множества A3: 2n n; счетность множества A4 установлена в примере 1.19; Установить счетность множеств можно также, используя следующие теоремы о счетных множествах (приводятся без доказательств). Теорема 1. Всякое бесконечное подмножество счетного множества счетно. Пример 1.21. Множество A = {3, 6, …, 3n,…} счетно, т.к. A – бесконечное подмножество множества натуральных чисел, A N. Теорема 2. Объединение конечной или счетной совокупности счетных множеств счетно. Пример 1.22. Множество A = {0, 1, …, n,…} неотрицательных целых чисел счетно, множество B = {0, –1, …, –n,…} неположительных целых чисел тоже счетно, поэтому множество всех целых чисел С = АB = {…, –n, …– 2, –1, 0, 1, 2, …, n, …} тоже счетно. Теорема 3. Множество всех рациональных чисел, т.е. чисел вида 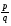 , где p и qцелые числа, счетно. , где p и qцелые числа, счетно.Теорема 4. Если А = {a1, a2, …} и B = {b1, b2, …} – счетные множества, то множество всех пар С = {(ak, bn), k = 1, 2,…; n = 1, 2, …} счетно. Пример 1.23. Геометрический смысл пары (ak, bn) – точка на плоскости с рациональными координатами (ak, bn). Поэтому можно утверждать, что множество всех точек плоскости с рациональными координатами счетно. Теорема 5. Множество всех многочленов P(x) = a0 +a1x + a2x2 + … + anxn любых степеней с рациональными коэффициентами a0,a1, a2, … anсчетно. Теорема 6. Множество всех корней многочленов любых степеней с рациональными коэффициентами счетно. 1.7. Множества мощности континуума Существуют бесконечные множества, элементы которых нельзя перенумеровать. Такие множества называются несчетными. Теорема Кантора. Множество всех точек отрезка [0, 1] несчетно. Доказательство. Пусть множество точек отрезка [0, 1] счетно. Значит, эти точки можно перенумеровать, т. е. расположить в виде последовательности x1, x2 … xn, … . 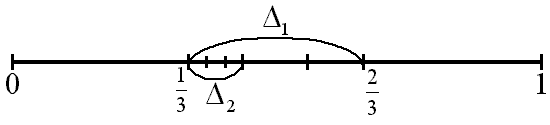 Рис. 1.7 Разобьем отрезок [0, 1] на три равные части. Где бы ни находилась точка x1, она не может принадлежать всем отрезкам 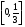 , , 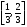 , , 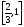 . Поэтому среди них есть отрезок 1, не содержащий точку x1 (рис. 1.7). Возьмем этот отрезок 1 и разделим его на три равные части. Среди них всегда есть отрезок 2, не содержащий точку x2. Разделим этот отрезок на три равные части и т. д. Получим последовательность отрезков 1 2 3 …n … . В силу аксиомы Кантора сходится к некоторой точке x при n . По построению эта точка x принадлежит каждому отрезку 1, 2, 3,…, n, …, т. е. она не может совпадать ни с одной из точек x1, x2, … xn, …, т. е. последовательность x1, x2 … xn, …не исчерпывает всех точек отрезка [0, 1], что противоречит первоначальному предположению. Теорема доказана. . Поэтому среди них есть отрезок 1, не содержащий точку x1 (рис. 1.7). Возьмем этот отрезок 1 и разделим его на три равные части. Среди них всегда есть отрезок 2, не содержащий точку x2. Разделим этот отрезок на три равные части и т. д. Получим последовательность отрезков 1 2 3 …n … . В силу аксиомы Кантора сходится к некоторой точке x при n . По построению эта точка x принадлежит каждому отрезку 1, 2, 3,…, n, …, т. е. она не может совпадать ни с одной из точек x1, x2, … xn, …, т. е. последовательность x1, x2 … xn, …не исчерпывает всех точек отрезка [0, 1], что противоречит первоначальному предположению. Теорема доказана.Множество, эквивалентное множеству всех точек отрезка [0, 1] называется множеством мощности континуума. Так как множества точек интервалов, отрезков и всей прямой эквивалентны между собой, то все они имеют мощность континуума. Чтобы доказать, что данное множество имеет мощность континуума, достаточно указать взаимно однозначное соответствие между данным множеством и множеством точек отрезка, интервала или всей прямой. Пример 1.24. Из рис. 1.8 следует, что множество точек параболы y= x2 эквивалентно множеству точек прямой – < x < и, следовательно, имеет мощность континуума. 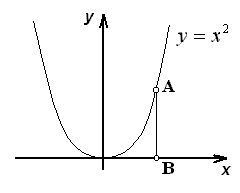 Рис.1.8 Установить мощность континуума можно также, используя следующие теоремы о множествах мощности континуума (приводятся без доказательств). Теорема 1. Множество всех подмножеств счетного множества счетно. Теорема 2. Множество иррациональных чисел имеет мощность континуума. Теорема 3. Множество всех точек n-мерного пространства при любом n имеет мощность континуума. Теорема 4. Множество всех комплексных чисел имеет мощность континуума. Теорема 5. Множество всех непрерывных функций, определенных на отрезке [a, b] имеет мощность континуума. Итак, мощности бесконечных множеств могут различаться. Мощность континуума больше, чем мощность счетного множества. Ответ на вопрос, существуют ли множества более высокой мощности, чем мощность континуума, дает следующая теорема (приводится без доказательства). Теорема о множествах высшей мощности. Множество всех подмножеств данного множества имеет более высокую мощность, чем данное множество. Из этой теоремы следует, что множеств с максимально большой мощностью не существует. Контрольные вопросы к теме 1 1. Пусть a А. Следует ли отсюда, что {a} 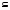 А? А?2. В каком случае А 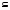 АВ? АВ?3. Назовите множество, которое является подмножеством любого множества. 4. Может ли быть множество эквивалентно своему подмножеству? 5. Мощность какого множества больше: множества натуральных чисел или множества точек отрезка [0, 1]? |
