Вариант № 15
1. В день авиации на аэродроме всех желающих катали на самолете, планере, дельтаплане. На самолете прокатились 30 человек, на планере – 20, на дельтаплане – 15. И на самолете, и на планере каталось 10 человек, на самолете и дельтаплане – 12, На планере и дельтаплане – 5. Два человека прокатились и на самолете, и на планере, и на дельтаплане. Сколько было желающих прокатиться?
2. Верно или неверно равенство: (A È B) \ A = B \ A ?
3. Привести пример двух множеств А и В, таких, что мощность множества А больше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества 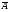 С È С È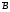 С. С.
5. Доказать, что множества A = {y: y = lnx, 0 < x < ¥} и B = {y: y = sinx, –¥ <x < ¥} эквивалентны.
Вариант № 16
1. Все грибники вернулись домой с полными корзинами. У десятерых из них в корзинах были белые грибы, у восемнадцати – подберезовики, у двенадцати – лисички. Белые и подберезовики были в шести корзинах, белые и лисички – в четырех, Подберезовики и лисички – в пяти. Все три вида грибов были у двух грибников. Сколько было грибников?
2. Верно или неверно равенство: (A È B) \ (AB) = A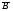 È È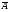 B? B?
3. Доказать, что множество точек A= {(x, y): y = ½x½, -, – 1 £ x£ 1} несчетно.
4. Нарисовать диаграмму Эйлера-Венна для множества 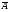 (B È C ) . (B È C ) .
5. Пусть A– множество точек отрезка [0, 1], а B – множество всех точек числовой оси. Какие из следующих отношений справедливы: а) A=B; б) A
B; в) AÉB; г) AÊB; д) AËB; е) AÎB.
Вариант № 17
1. Все туристы взяли в поход консервы. Шесть человек взяли тушенку, пять – сгущенку, восемь – кашу (с мясом). У троих в рюкзаках была тушенка и сгущенка, у двоих – тушенка и каша, у троих – сгущенка и каша, и только в одном рюкзаке лежали все три вида консервов. Сколько было туристов?
2. Верно или неверно равенство: 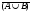 С С \ (С (AÈB))? С С \ (С (AÈB))?
3. Пусть A – множество решений уравнения x2 – 3x + 2 = 0. Записать это множество двумя различными способами.
4. Нарисовать диаграмму Эйлера-Венна для множества (BC) \ A .
5. Эквивалентны ли множества A = {x: x2 –3x + 2 = 0} и B = {2, 3}?
Вариант № 18
1. Было опрошено 70 человек. В результате опроса выяснили, что 45 человек знают английский язык, 29 – немецкий и 9 – оба языка. Сколько человек из опрошенных не знает ни английского, ни немецкого языков?
2. Верно или неверно равенство: (A È B) \ (AB) = A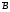 È È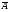 B? B?
3. Найти все подмножества множества A= {x, y, z}.
4. Нарисовать диаграмму Эйлера-Венна для множества 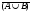 С. С.
5. Счетно ли множество {(x, y): y = 3x, 0<x< ¥}?
Вариант № 19
1. В туристической группе 10 человек знают английский язык, 10 – итальянский, 6 – испанский. По два языка знают: 6 человек – английский и итальянский, 4 – английский и испанский, 3 – итальянский и испанский. Один человек знает все три языка. Сколько туристов в группе?
2. Упростить 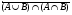 . .
3. Привести пример двух множеств А и В, таких, что мощность множества А больше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества С \ (С (AÈB)).
5. Эквивалентны ли множества A = { 2n, n = 1, 2, …} и B = {n2, n = 1, 2, …}?
Вариант № 20
1. Предприятие объявило набор рабочих на должности токаря, слесаря и сварщика. В отдел кадров обратились 25 человек. Из них 10 человек владели профессией токаря, 15 – слесаря, 12 – сварщика. Профессией и токаря и слесаря владели 6 человек, и токаря, и сварщика – 5 человек, и слесаря и сварщика – 3 человека. Сколько человек владеют всеми тремя профессиями?
2. Верно или неверно равенство: 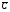 \ \ 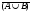 = = 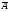 \ \ 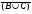 ? ?
3. Привести примеры множеств А, В и С , для которых одновременно выполняются равенства А È В È С = А и А В С = С.
4. Нарисовать диаграмму Эйлера-Венна для множества 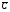 \ \ 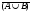 . .
5. Можно ли построить взаимно-однозначное соответствие между множеством рациональных чисел отрезка [0, 1] и множеством рациональных чисел из этого интервала? Ответ обосновать.
Вариант № 21
1. Оказалось, что в группе туристов 15 человек были раньше во Франции, 19 – в Италии, 8 – в Германии. 9 туристов были во Франции и в Италии, 7 – во Франции и в Германии, 6 – и в Италии, и в Германии. 4 туриста были во всех трех странах. Сколько туристов были хотя бы в одной из трех стран?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В С) = (А \ В) 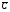 ? ?
3. Привести примеры множеств А и В, для которых равенство 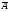 È В = È В = 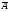
а) выполняется; б) не выполняется.
4. Нарисовать диаграмму Эйлера-Венна для множества А (В È 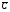 ). ).
5. Найти мощность множества точек окружности с центром в точке (0, 0) и радиусом 1.
Вариант № 22
1. Группе студентов из 30 человек была предложена контрольная работа из трех задач. Первую задачу решили 15 студентов, вторую – 13, третью – 12. Первую и вторую задачи решили 7 человек, первую и третью – 6, вторую и третью – 5 человек. Все три задачи решили 2 студента. Сколько студентов из группы не решили ни одной задачи?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В È С) = (А \ В) 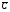 ? ?
3. Привести пример двух бесконечных множеств А и В, таких, что мощность множества А больше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества А В 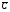 . .
5. Найти мощность множества точек гиперболы y = 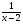 при x Î ( 3, ¥). при x Î ( 3, ¥).
Вариант № 23
1. Анализ историй болезней группы из 20 детей показало, что 10 детей болели ветрянкой, 6 – корью, 5 – свинкой. Ветрянкой и корью болели 3 ребенка, ветрянкой и свинкой – 3, корью и свинкой – 2. Всеми тремя болезнями болел один ребенок. Сколько детей не болели ни одной из перечисленных болезней?
2. Верно или неверно равенство: 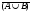 С) С) 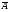 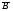 С? С?
3. Доказать, что множество точек A= {(x, y): y = ½x+1½, – 1 £ x£ 1} несчетно.
4. Нарисовать диаграмму Эйлера-Венна для множества (BC) \ A .
5. Пусть A– множество точек отрезка [1, 2], а B – множество точек интервала (0, 3). Какие из следующих отношений справедливы: а) A=B; б) A
B; в) AÌB; г) AÊB; д) AËB; е) AÎB.
Вариант № 24
1. В книжный киоск привезли для продажи 100 книг Пушкина, Лермонтова и Тургенева. Книги Пушкина купили 60 человек, книги Лермонтова – 50, книги Тургенева – 30 человек. Книги Пушкина и Лермонтова купили 40 человек, книги Пушкина и Тургенева – 20, книги Лермонтова и Тургенева – 10 человек. Пять человек купили книги всех трех писателей. Сколько человек не купили ни одной из перечисленных книг?
2. Верно или неверно равенство: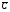 \ \ 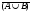 = = 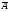 \ \ 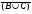 ? ?
3. Привести примеры множеств А, В и С таких, что равенство А È В È С = С
а) справедливо; б) несправедливо.
4. Нарисовать диаграмму Эйлера-Венна для множества 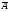 \ \ 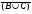 . .
5. Можно ли построить взаимно-однозначное соответствие между множеством натуральных чисел N и множеством действительных чисел отрезка [0, 1]? Ответ обосновать.
Вариант № 25
1. Группа научных работников состоит из 100 человек. Из них 70 человек владеют английским языком, 50 – немецким, 40 – французским, 30 – английским и немецким, 25 – английским и французским, 15 – французским и немецким. Хотя бы один язык знает каждый научный работник. Сколько человек владеют всеми тремя языками?
2. Упростить: (A\ (AB)) È В.
3. Привести примеры множеств А, В и С так, чтобы AÎB, В Ì С.
4. Нарисовать диаграмму Эйлера-Венна для множества 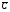 \ \ 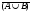 . .
5. Можно ли утверждать, что множество всех положительных пятизначных чисел счетно? Ответ обосновать.
Вариант № 26
1. На курсы иностранных языков записалось 100 человек. Оказалось, что 70 человек будут изучать английский язык, 60 человек – французский и 30 человек - немецкий. Английский и французский собираются изучать 40 человек, английский и немецкий – 20, французский и немецкий – 10. Сколько студентов будут изучать все три языка?
2. Упростить равенство: (A С )\ (С (AÈB)).
3. Привести пример двух различных бесконечных множеств А и В, таких, что мощность множества А равна мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества 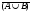 С). С).
5. Эквивалентны ли множества A = {x: x3 – 1 = 0} и B = {x: x2 – 3x + 2 = 0}?
Вариант № 27
В команде бегунов десять спортсменов бегают на длинные дистанции, восемнадцать – на средние, двенадцать – на короткие. На длинные и средние дистанции бегают пять спортсменов, на средние и короткие – шесть. На длинные и короткие дистанции не бегает никто. Сколько бегунов в команде?
2. Верно или неверно равенство: 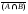 ÈС) ÈС) 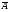 È È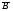 È С? È С?
3. В каком случае AÈB= А В?
4. Нарисовать диаграмму Эйлера-Венна для множества 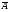 È(BC ) . È(BC ) .
5. Можно ли утверждать, что множество всех положительных чисел имеет меньшую мощность, чем множество всех действительных чисел? Ответ обосновать.
Вариант № 28
1. В студенческой группе 25 человек. Чтобы получить допуск на экзамен по данному курсу необходимо защитить курсовую работу, выполнить лабораторную работу и сдать зачет. 15 студентов защитили курсовую работу, 20 выполнили лабораторную работу, 17 сдали зачет. Защитили курсовую работу и выполнили лабораторную работу 12 человек. Защитили курсовую работу и сдали зачет 13 человек. Выполнили лабораторную работу и сдали зачет 16 человек. Сколько студентов допущено к экзамену?
2. Упростить: 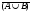 ( (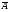 È È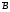 ). ).
3. Привести пример двух бесконечных множеств А и В, таких, что мощность множества А меньше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества 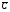 \ \ 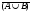 . .
5. Эквивалентны ли множество рациональных чисел отрезка [0, 1] и множество рациональных чисел из этого интервала? Ответ обосновать.
Вариант № 29
1. В классе 20 детей. Из них 10 дополнительно занимаются в музыкальной школе, 6 – теннисом, 5 – китайским языком. Музыкальную школу и занятия по теннису посещают три ребенка, музыкой и китайским языком занимаются трое, теннисом и китайским языком двое. Всеми тремя видами дополнительных занятий занимается один ребенок. Сколько детей не занимается ни одним из перечисленных занятий?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В ÈС) = (А \В) 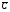 ? ?
3. Доказать, что множество точек A = {y: y = 2n, n = 1, 2, …} счетно.
4. Нарисовать диаграмму Эйлера-Венна для множества A 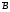 È È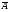 B . B .
5. Эквивалентны ли множества A = {(x, y): y = x2, 1< x <2} и B = {(x, y): y = 2x, 3< x < ¥}?
Вариант № 30
1. В цеху имеется 25 станков, которые могут выполнять три вида операций: А, В и С. Из них 10 станков выполняют операцию А, 15 – В, 12 – С. Операции А и В могут быть выполнены на 6 станках, А и С – на 5, В и С – на 3 станках. Сколько станков могут выполнять все три операции?
2. Верно или неверно равенство: 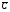 \ \ 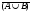 = = 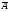 \ \ 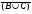 ? ?
3. Привести примеры множеств А, В и С , для которых одновременно выполняются равенства А È В È С = А и А В С = С.
4. Нарисовать диаграмму Эйлера-Венна для множества 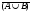 С. С.
5. Можно ли построить взаимно-однозначное соответствие между множеством действительных чисел отрезка [0, 1] и множеством действительных чисел интервала (0, 1)? Ответ обосновать.
2. Раздел «Отношения. Функции»
Вариант № 1
1. Задано бинарное отношение = {<1, 1>, <1, 3>, <3, 1>, <3, 4>, <4, 3>}.
Найти D(), R(), Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не рефлексивного, не симметричного и транзитивного.
3. Дана функция f(x) = x2 + ex, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 2
1. Задано бинарное отношение = {<1, 3>, <3, 1>, <3, 4>, <4, 3>, <4, 4>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не симметричного, но рефлексивного и транзитивного.
3. Дана функция f(x) = x2 + e-x, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 3
1. Задано бинарное отношение = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 1>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, но рефлексивного и симметричного.
3. Дана функция f(x) = x + ex, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 4
1. Задано бинарное отношение = {<1, 1>, <1, 2>, <2, 1>, <3, 3>, <4, 4>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xy, задаваемое равенством x2 + y2 = 25?
3. Дана функция f(x) = x3 + ex, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 5
1. Задано бинарное отношение = {<1, 2>, <2, 1>, <3, 4>, <4, 3>, <4, 4>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не симметричного, не рефлексивного и транзитивного.
3. Дана функция f(x) = x + e--x, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 6
1. Задано бинарное отношение = {<2, 2>, <2, 3>, <3, 2>, <3, 1>, <4, 1>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.
3. Дана функция f(x) = x + ex, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 7
1. Задано бинарное отношение = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного, симметричного и транзитивного.
3. Дана функция f(x) = x 2 +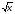 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 8
1. Задано бинарное отношение = {<2, 2>, <2, 3>, <3, 2>, <3, 4>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и антисимметричного.
3. Дана функция f(x) = x +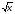 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 9
1. Задано бинарное отношение = {<1, 2>, <2, 3>, <1, 3>, <1, 1>, <2, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного, рефлексивного и симметричного.
3. Дана функция f(x) = sinx +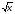 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 10
1. Задано бинарное отношение = {<1, 1>, <2, 3>, <1, 3>, <3, 1>, <3, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xy, задаваемое равенством x = 2y?
3. Дана функция f(x) = lnx +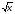 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 11
1. Задано бинарное отношение = {<1, 1>, <2, 4>, <1, 4>, <4, 1>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и не симметричного.
3. Привести пример функции f(x), отображающей множество действительных чисел R во множество действительных чисел, R® R и являющейся сюръективной, инъективной, биективной.
Вариант № 12
1. Задано бинарное отношение = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xy, задаваемое равенством x + y = 100?
3. Привести пример функции f(x), отображающей множество действительных чисел R во множество действительных чисел, R® R и не являющейся сюръективной, инъективной, биективной.
Вариант № 13
1. Задано бинарное отношение = {<1, 1>, <1, 2>, <2, 1>, <3, 1>, <1, 3>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.
3. Привести пример функции f(x), отображающей множество действительных чисел R во множество действительных чисел, R® R и являющейся сюръективной, но не инъективной.
Вариант № 14
1. Задано бинарное отношение = {<1, 1>, <2, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного, симметричного и транзитивного.
3. Дана функция f(x) = x 2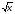 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 15
1. Задано бинарное отношение = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения эквивалентности.
3. Дана функция f(x) = x 2 +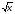 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 16
1. Задано бинарное отношение = {<b, b>, <b, c>, <c, b>, <c, a>, <d, a>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения частичного порядка на множестве целых чисел..
3. Дана функция f(x) = x 2 +lnx, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 17
1. Задано бинарное отношение = {<x, x>, <y, z>, <x, z>, <z, x>, <z, y>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения транзитивного и симметричного.
3. Дана функция f(x) = x +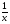 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 18.
1. Задано бинарное отношение = {<1, 1>, <1, a>, <a, 1>, <a, 4>, <4, a>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения рефлексивного и транзитивного.
3. Дана функция f(x) = x 2 + 2x, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 19
1. Задано бинарное отношение = {<1, 1>, <2, 2>, <2, 3>, <3, 2>, <3, 3>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xy, задаваемое равенством x 2 – y2 = 0?
3. Дана функция f(x) = 2x +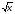 , отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 20
1. Задано бинарное отношение = {<1, 1>, <1, 2>, <2, 1>, <3, 3>, <4, 4>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не рефлексивного, не симметричного и не транзитивного.
3. Дана функция f(x) = x3ex, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 21
1. Задано бинарное отношение = {<1, 3>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения частичного порядка на множестве треугольников на плоскости.
3. Привести пример функции f(x), отображающей множество действительных чисел R во множество действительных чисел, R® R и не являющейся сюръективной, инъективной, биективной.
Вариант № 22
1. Задано бинарное отношение = {<1, 2>, <2, 2>, <2, 1>, <2, 3>, <3, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xy, задаваемое равенством x = – y?
3. Дана функция f(x) = lnx +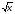 , отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество положительных действительных чисел во множество всех действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 23
1. Задано бинарное отношение = {<1, 1>, <2, 2>, <2, 1>, <2, 3>, <3, 2>, <3, 3>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением частичного полрядка на множестве действительных чисел отношение xy, задаваемое неравенством x 2 – y2 0?
3. Дана функция f(x) = ex +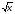 , отображающая множество положительных действительных чисел на множество положительных действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество положительных действительных чисел на множество положительных действительных чисел. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 24
1. Задано бинарное отношение = {<1, 1>, <1, 2>, <2, 1>, <3, 1>, <3, 2> <1, 3>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.
3. Привести пример функции f(x), отображающей множество действительных чисел R во множество неотрицательных действительных чисел, R® [0, ) и являющейся сюръективной, но не инъективной.
Вариант № 25
1. Задано бинарное отношение = {<1, 2>, <2, 1>, <2, 3>, <1, 3>, <3, 1>, <3, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xy, задаваемое неравенством x y?
3. Дана функция f(x) = lnx + 2x, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 26
1. Задано бинарное отношение = {<2, 2>, <2, 4>, <1, 4>, <4, 1>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и не симметричного.
3. Привести пример функции f(x), отображающей множество действительных чисел R во множество действительных чисел, R® R и являющейся сюръективной и неинъективной.
Вариант № 27
1. Задано бинарное отношение = {<1, 1>, <3, 4>, <1, 4>, <4, 1>, <4, 3>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Будет ли отношением эквивалентности на множестве действительных чисел отношение xy, задаваемое равенством xy = 100?
3. Привести пример функции f(x), отображающей множество действительных чисел R во множество действительных чисел, R® R и не являющейся сюръективной, инъективной, биективной.
Вариант № 28
1. Задано бинарное отношение = {<1, 1>, <2, 2>, <3, 3>, <3, 1>, <1, 3>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения не транзитивного, не рефлексивного и симметричного.
3. Привести пример функции f(x), отображающей множество действительных чисел R во множество действительных чисел, R® R и являющейся сюръективной, но не инъективной.
Вариант № 29
1. Задано бинарное отношение = {<1, 1>, <2, 2>, <4, 4>, <2, 1>, <2, 4>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения частичного порядка.
3. Дана функция f(x) = x 2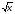 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
Вариант № 30
1. Задано бинарное отношение = {<1, 1>, <1, 2>, <2, 1>, <2, 4>, <4, 2>}.
Найти D(), R(),  , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным? , -1. Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
2. Привести пример отношения эквивалентности.
3. Дана функция f(x) = x 2 +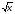 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему? , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
3. Раздел «Графы»
1. Описать граф, заданный матрицей смежности, используя как можно больше характеристик. Составить матрицу инцидентности и связности (сильной связности).
2. Пользуясь алгоритмом Форда-Беллмана, найти минимальный путь из x1 вx7 в ориентированном графе, заданном матрицей весов.
3. Пользуясь алгоритмом Краскала, найти минимальное остовное дерево для графа, заданного матрицей длин ребер.
Варианты заданий
1 .1. 0 1 1 0 1 1 2. ¥ 4 6 12 ¥ ¥ ¥ 3. ¥ 12 6 20 14
1 0 0 1 0 0 ¥ ¥ ¥ 13 7 ¥ ¥ 12 ¥ 2 4 6
1 0 0 0 1 0 ¥ ¥ ¥ 5 ¥ 3 ¥ 6 2 ¥ 10 12
0 1 0 0 1 0 ¥ ¥ ¥ ¥ 10 9 ¥ 20 4 10 ¥ 6
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 8 14 6 12 6 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
2 .1. 0 0 0 0 0 1 2. ¥ 1 3 9 ¥ ¥ ¥ 3. ¥ 1 ¥ 4 5
0 0 1 1 1 0 ¥ ¥ ¥ 10 4 ¥ ¥ 1 ¥ 2 ¥ 1
0 0 0 0 0 0 ¥ ¥ ¥ 2 ¥ 1 ¥ ¥ 2 ¥ 1 1
1 0 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 ¥ 1 ¥ 3
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8
¥ ¥ ¥ ¥ ¥ ¥ ¥
3 .1. 0 1 0 1 0 0 2. ¥ 3 5 11 ¥ ¥ ¥ 3. ¥ 6 3 10 7
1 0 0 1 0 0 ¥ ¥ ¥ 12 6 ¥ ¥ 6 ¥ 1 2 3
0 0 0 0 1 1 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 0 0 1 1 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 5 ¥ 3
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 3 6 3 ¥
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
4.1. 0 0 0 0 0 1 2. ¥ ¥ 5 4 2 2 9 3. ¥ 7 2 11 7
1 0 1 0 1 1 ¥ ¥ 1 1 ¥ 1 1 7 ¥ 3 ¥ 4
1 0 0 0 0 0 2 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 0 1 0 0 1 ¥ 2 1 ¥ 1 ¥ ¥ 11 ¥ 1 ¥ 3
0 1 1 1 0 0 ¥ ¥ 2 2 ¥ 1 6 7 4 5 3 ¥
0 0 1 0 0 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
5 .1. 0 0 0 1 1 0 2. ¥ 4 ¥ ¥ 3 1 ¥ 3. ¥ 2 ¥ 5 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 2 ¥ 8 ¥ 7
1 0 0 0 0 0 1 1 ¥ ¥ ¥ ¥ 1 ¥ 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 5 ¥ 10 ¥ 13
1 0 0 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 13 ¥
0 1 0 1 0 0 ¥ 3 ¥ 2 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
6.1. 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ ¥ 2 12 3. ¥ 1 5 4 5
0 0 1 1 1 1 1 ¥ ¥ ¥ 1 2 4 1 ¥ 2 6 1
1 1 0 0 1 0 2 1 ¥ ¥ 1 ¥ 2 5 2 ¥ 1 7
0 1 0 0 0 1 ¥ 1 1 ¥ ¥ 1 ¥ 4 6 1 ¥ 4
1 1 1 0 0 0 1 2 ¥ 2 ¥ ¥ ¥ 5 1 7 4 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
7.1. 0 0 1 1 0 0 2. ¥ 3 4 9 ¥ ¥ ¥ 3. ¥ 4 3 5 6
1 0 0 0 0 1 12 ¥ ¥ 10 4 ¥ ¥ 4 ¥ 2 ¥ 1
1 0 0 0 1 0 ¥ ¥ ¥ 2 ¥ 1 ¥ 3 2 ¥ 1 1
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 5 ¥ 1 ¥ 3
0 0 1 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 6 1 1 3 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8
¥ ¥ ¥ ¥ ¥ ¥ ¥
8 .1. 0 1 1 0 1 1 2. ¥ 2 5 8 9 ¥ ¥ 3. ¥ 1 3 4 5
1 0 1 1 0 1 ¥ ¥ ¥ 10 4 ¥ ¥ 1 ¥ 2 9 1
1 1 0 0 1 1 5 3 ¥ 2 1 ¥ ¥ 3 2 ¥ 1 1
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 9 1 ¥ 3
1 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥
1 1 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 9
¥ ¥ ¥ ¥ ¥ ¥ ¥
9 .1. 0 1 0 1 1 1 2. ¥ 2 5 14 ¥ ¥ ¥ 3. ¥ 5 3 10 7
1 0 0 1 0 0 11 ¥ ¥ 12 6 ¥ ¥ 5 ¥ 1 2 4
0 0 0 1 1 0 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 1 0 1 0 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 5 ¥ 3
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 4 6 3 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
10.1 0 1 1 0 1 1 2. ¥ ¥ 5 4 2 3 9 3. ¥ 7 2 11 7
1 0 0 1 1 1 ¥ ¥ 1 1 ¥ 1 6 7 ¥ 3 ¥ 4
1 0 0 0 1 0 4 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 1 0 0 0 1 ¥ 2 1 ¥ 1 ¥ ¥ 11 ¥ 1 ¥ 3
1 1 1 0 0 1 ¥ ¥ 2 2 ¥ 1 6 7 4 5 3 ¥
1 1 0 1 1 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
11.1. 0 0 1 0 1 0 2. ¥ 4 9 ¥ 3 1 ¥ 3. ¥ 1 ¥ 4 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 1 ¥ 8 ¥ 7
1 0 0 0 1 0 1 1 ¥ ¥ 10 ¥ 1 ¥ 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 4 ¥ 10 ¥ 13
1 0 1 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 13 ¥
0 1 0 1 0 0 ¥ 3 ¥ 1 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
12.1 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ 10 2 12 3. ¥ 1 5 4 6
0 0 0 1 0 1 1 ¥ ¥ ¥ 1 2 4 1 ¥ 2 6 3
1 1 0 0 1 1 2 1 ¥ ¥ 1 ¥ 2 5 2 ¥ 1 7
0 0 0 0 0 0 ¥ 1 1 ¥ ¥ 1 15 4 6 1 ¥ 4
1 1 1 0 0 0 1 2 ¥ 2 ¥ ¥ ¥ 6 3 7 4 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
13.1. 0 0 0 0 0 0 2. ¥ 5 6 15 ¥ ¥ ¥ 3. ¥ 12 6 10 4
1 0 0 1 0 1 ¥ ¥ ¥ 13 7 ¥ ¥ 12 ¥ 2 5 6
1 0 0 0 1 0 ¥ ¥ ¥ 4 ¥ 3 ¥ 6 2 ¥ 10 12
1 1 1 0 0 0 ¥ ¥ ¥ ¥ 10 9 ¥ 10 5 10 ¥ 6
1 1 0 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8 4 6 12 6 ¥
0 1 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
14.1. 0 0 1 1 0 0 2. ¥ 2 3 9 ¥ ¥ ¥ 3. ¥ 3 2 4 5
1 0 0 0 0 1 12 ¥ ¥ 10 4 ¥ ¥ 3 ¥ 2 ¥ 1
1 0 0 0 1 0 ¥ ¥ ¥ 2 ¥ 1 ¥ 2 2 ¥ 1 1
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 ¥ 1 ¥ 3
0 0 1 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 5 5 1 1 3 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 8
¥ ¥ ¥ ¥ ¥ ¥ ¥
15.1. 0 1 0 1 0 0 2. ¥ 2 5 10 ¥ ¥ ¥ 3. ¥ 6 3 10 4
1 0 0 1 0 0 ¥ ¥ ¥ 12 6 ¥ ¥ 6 ¥ 1 2 3
0 0 0 0 1 1 ¥ ¥ ¥ 3 ¥ 1 ¥ 3 1 ¥ 8 6
1 1 0 0 1 1 ¥ ¥ ¥ ¥ 9 8 ¥ 10 2 8 ¥ 3
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 7 4 3 6 3 ¥
0 0 1 1 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
16.1. 0 0 0 0 1 1 2. ¥ ¥ 5 4 2 2 10 3. ¥ 4 2 10 6
0 0 1 1 0 0 ¥ ¥ 2 1 ¥ 2 1 4 ¥ 3 ¥ 4
0 1 0 0 1 0 2 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 1 0 0 0 1 ¥ 2 1 ¥ 1 ¥ ¥ 10 ¥ 1 ¥ 3
1 0 1 0 0 0 ¥ ¥ 2 2 ¥ 1 6 6 4 5 3 ¥
1 0 0 1 0 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
17.1 0 0 1 0 1 0 2. ¥ 4 9 8 3 1 ¥ 3. ¥ 2 ¥ 3 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 2 ¥ 8 ¥ 7
1 0 0 0 1 0 1 1 ¥ ¥ ¥ ¥ 1 ¥ 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 3 ¥ 10 ¥ 12
1 0 1 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 12 ¥
0 1 0 1 0 0 ¥ 3 ¥ 2 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
18.1. 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ 10 2 12 3. ¥ 1 3 4 5
0 0 0 0 0 0 1 ¥ ¥ ¥ 1 2 4 1 ¥ 2 6 8
1 0 0 0 1 0 2 1 ¥ ¥ 1 ¥ 2 3 2 ¥ 1 7
0 1 0 0 0 1 ¥ 1 1 ¥ ¥ 1 ¥ 4 6 1 ¥ 4
1 0 1 0 0 0 1 2 9 2 ¥ ¥ ¥ 5 8 7 4 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
19.1. 0 1 1 0 1 1 2. ¥ 3 5 12 20 ¥ ¥ 3. ¥ 1 6 5 14
1 0 0 1 0 0 ¥ ¥ ¥ 13 8 ¥ ¥ 1 ¥ 3 4 6
1 0 0 1 1 1 ¥ ¥ ¥ 5 ¥ 3 ¥ 6 3 ¥ 10 12
0 1 1 0 1 1 ¥ ¥ ¥ ¥ 10 9 ¥ 5 4 10 ¥ 6
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 8 14 6 12 6 ¥
1 0 1 1 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
20.1. 0 1 0 0 1 0 2. ¥ 1 5 7 9 ¥ ¥ 3. ¥ 6 3 4 5
1 0 0 1 0 0 ¥ ¥ ¥ 10 4 ¥ ¥ 6 ¥ 2 9 1
1 0 0 0 1 1 5 3 ¥ ¥ 1 ¥ ¥ 3 2 ¥ 1 4
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 9 1 ¥ 3
0 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 4 5 1 4 3 ¥
0 1 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 9
¥ ¥ ¥ ¥ ¥ ¥ ¥
21.1. 0 1 0 1 1 1 2. ¥ 1 5 15 ¥ ¥ ¥ 3. ¥ 5 3 6 7
1 0 0 1 0 0 ¥ ¥ 11 12 6 ¥ ¥ 5 ¥ 1 2 4
0 0 0 1 1 0 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 1 0 1 0 ¥ ¥ ¥ ¥ 9 8 ¥ 6 2 5 ¥ 3
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 7 7 4 6 3 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
22.1 0 0 1 0 1 0 2. ¥ ¥ 3 4 1 5 9 3. ¥ 7 2 11 3
0 0 0 0 0 0 ¥ ¥ 1 2 ¥ 1 6 7 ¥ 3 ¥ 4
0 1 0 0 1 1 4 ¥ ¥ 2 1 ¥ 3 2 3 ¥ 1 5
0 1 0 0 0 1 ¥ 2 3 ¥ 1 ¥ ¥ 11 ¥ 1 ¥ 3
1 1 1 0 0 0 ¥ ¥ 2 2 ¥ 1 6 3 4 5 3 ¥
0 0 0 1 1 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
23.1. 0 0 1 0 1 0 2. ¥ 4 9 ¥ 3 1 ¥ 3. ¥ 1 9 4 5
0 0 0 1 0 1 3 ¥ 2 1 ¥ ¥ 4 1 ¥ 8 ¥ 7
1 0 0 0 1 0 1 1 ¥ ¥ 10 14 1 9 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 4 ¥ 10 ¥ 13
1 0 1 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 13 ¥
0 1 0 1 0 0 ¥ 3 ¥ 1 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
24.1 0 0 1 0 1 0 2. ¥ ¥ 8 ¥ 10 3 12 3. ¥ 3 2 4 6
0 0 0 1 0 0 1 ¥ ¥ ¥ 1 2 3 3 ¥ 5 6 3
0 1 0 0 1 0 2 1 ¥ ¥ 1 ¥ 2 2 5 ¥ 1 7
0 0 0 0 0 1 ¥ 1 1 ¥ ¥ 1 15 4 6 1 ¥ 4
0 1 1 0 0 0 1 2 ¥ 2 ¥ ¥ ¥ 6 3 7 4 ¥
0 1 0 0 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
25.1. 0 0 1 0 0 1 2. ¥ ¥ 5 4 2 2 10 3. ¥ 1 2 8 5
0 0 1 1 1 1 ¥ ¥ 2 1 ¥ 2 1 1 ¥ 3 ¥ 4
1 1 0 0 0 0 2 ¥ ¥ 1 1 ¥ 3 2 3 ¥ 1 5
0 1 0 0 0 1 12 2 1 ¥ 1 ¥ ¥ 8 ¥ 1 ¥ 3
0 1 0 0 0 1 ¥ ¥ 2 2 ¥ 1 6 5 4 5 3 ¥
1 1 0 1 1 0 1 5 ¥ 1 1 ¥ ¥
2 ¥ 1 ¥ 1 2 ¥
26.1. 0 0 0 0 1 0 2. ¥ 4 9 8 3 2 ¥ 3. ¥ 2 9 3 5
0 0 0 1 0 0 3 ¥ 2 1 ¥ ¥ 5 2 ¥ 8 ¥ 7
1 0 0 0 1 0 2 1 ¥ ¥ ¥ ¥ 1 9 8 ¥ 10 1
0 1 0 0 0 1 ¥ 3 1 ¥ 1 ¥ ¥ 3 ¥ 10 ¥ 12
0 0 0 0 0 0 ¥ ¥ 2 ¥ ¥ 1 5 5 7 1 12 ¥
0 1 0 0 0 0 ¥ 3 ¥ 2 2 ¥ ¥
¥ ¥ 2 ¥ ¥ 2 ¥
27.1. 0 0 1 0 1 0 2. ¥ ¥ 9 ¥ 8 1 12 3. ¥ 1 3 7 2
0 0 1 1 1 1 1 ¥ ¥ ¥ 2 2 4 1 ¥ 5 6 8
1 1 0 0 1 0 2 1 ¥ ¥ 1 ¥ 2 3 5 ¥ 1 7
0 1 0 0 0 1 ¥ 1 1 ¥ ¥ 1 ¥ 7 6 1 ¥ 4
1 1 1 0 0 0 1 2 9 2 ¥ ¥ ¥ 2 8 7 4 ¥
0 1 0 1 0 0 ¥ ¥ ¥ ¥ 1 ¥ 8
¥ 2 1 ¥ 1 2 ¥
28.1. 0 1 1 0 1 1 2. ¥ 3 5 12 20 ¥ ¥ 3. ¥ 1 6 5 14
1 0 0 1 0 0 ¥ ¥ ¥ 13 8 ¥ ¥ 1 ¥ 3 4 6
1 0 0 1 1 1 ¥ ¥ ¥ 5 ¥ 3 ¥ 6 3 ¥ 10 12
0 1 1 0 1 1 ¥ ¥ ¥ ¥ 10 9 ¥ 5 4 10 ¥ 6
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 8 14 6 12 6 ¥
1 0 1 1 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 11
¥ ¥ ¥ ¥ ¥ ¥ ¥
29.1. 0 1 0 0 1 0 2. ¥ 1 8 6 7 ¥ ¥ 3. ¥ 2 3 4 5
1 0 0 1 0 0 ¥ ¥ ¥ 10 4 ¥ ¥ 2 ¥ 6 9 1
1 0 0 0 1 1 5 3 ¥ ¥ 1 ¥ ¥ 3 6 ¥ 1 4
0 1 0 0 0 1 ¥ ¥ ¥ ¥ 7 6 ¥ 4 9 1 ¥ 3
0 0 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 4 5 1 4 3 ¥
0 1 1 0 0 0 ¥ ¥ ¥ ¥ ¥ ¥ 9
¥ ¥ ¥ ¥ ¥ ¥ ¥
30.1. 0 1 0 1 1 1 2. ¥ 2 4 13 ¥ ¥ ¥ 3. ¥ 5 3 6 4
1 0 0 1 0 0 ¥ ¥ 11 12 6 ¥ ¥ 5 ¥ 1 2 7
0 0 0 1 1 0 ¥ ¥ ¥ 3 ¥ 2 ¥ 3 1 ¥ 5 6
1 1 1 0 1 0 ¥ ¥ ¥ ¥ 9 8 ¥ 6 2 5 ¥ 3
1 0 1 1 0 1 ¥ ¥ ¥ ¥ ¥ ¥ 7 4 7 6 3 ¥
1 0 0 0 1 0 ¥ ¥ ¥ ¥ ¥ ¥ 10
¥ ¥ ¥ ¥ ¥ ¥ ¥
4. Раздел «Булевы функции»
Для данной формулы булевой функции
а) найти ДНФ, КНФ, СДНФ, СКНФ методом равносильных преобразований;
б) найти СДНФ, СКНФ табличным способом (сравнить с СДНФ, СКНФ, полученными в пункте “а”);
в) указать минимальную ДНФ и соответствующую ей переключательную схему.
Варианты заданий
Функция
|
Функция
|
1. ((x V y) z) V x&y&z
2.(x&(y (xVz)))
3. (x (z&(y x)))
4.(xy) (xVz)
5.(x y) V (y z)
6. (x&y) ((x&z) x)
7. (y x) (x z)
8. (x&y) ((xVz) & y)
9. (xy) (xVz)
10. (x& y) ((xVz) y)
11.x (y (z y&z))
12. ((y& z) (xVz)) y
13. (x&(y (x z)))
14. (x (x&(yV(x y)Vx)))
15. (x z) V (y z)
|
16. (xy) (xVz)
17. x&y (x&z (xVy))
18. (y x) (x z)
19. (x&y z) (x z)
20. (x&y z) (x y)
21. x (y (z x))
22. y&z (xVz&y)
23. (x&(y (z y)))
24. x (x&(yV(x z)))
25. (x y)V (y&(xz))
26. (x y) (x z)
27. (x y) (x&z)
28. x (z (x Vy&z))
29. x&(y (z y))
30. (x z) V (y z)
|
Вопросы к экзамену по дисциплине «Дискретная математика»
1. Основные понятия теории множеств: множества, подмножества, пустое множество, универсальное множество, множество-степень.
2. Способы задания множеств.
3. Операции над множествами.
4. Геометрическое моделирование множеств. Диаграммы Эйлера - Венна.
5. Алгебра множеств. Основные тождества алгебры множеств.
6. Эквивалентность множеств. Свойство транзитивности. Мощность множества.
7. Мощность объединения конечных множеств.
8. Эквивалентность множества точек отрезков и интервалов. Теорема Бернштейна.
9. Счетные множества. Теоремы о счетных множествах.
10. Мощность множества точек отрезка [0, 1]. Теорема Кантора.
11. Множества мощности континуума. Теоремы о множествах мощности континуума.
12. Отношения. Основные понятия и определения. Бинарные отношения. Область определения, область значений и область задания бинарного отношения.
13. Операции над отношениями. Обратное отношение, Композиция отношений.
14. Свойства отношений. Рефлексивность, симметричность, транзитивность, эквивалентность.
15. Классы эквивалентности. Разбиение множеств.
16. Отношение частичного порядка.
17. Функция как бинарное отношение. Область определения и область значений функции. Равенство функций.
18. Сюръективные, инъективные, биективные функции.
19. Обратная функция. Композиция функций.
20. Способы задания функций.
21. Определение графа. Различные типы графов.
22. Матричные способы задания графов.
23. Изоморфизм графов.
24. Маршруты, циклы в неориентированном графе.
25. Пути, контуры в ориентированном графе.
26. Связность неориентированного графа. Матрица связности.
27. Связность ориентированного графа. Матрицы односторонней и сильной связности..
28. Экстремальные пути в нагруженных ориентированных графах.
29. Алгоритм Форда – Беллмана нахождения минимального пути.
30. Деревья. Остовные деревья.
31. Минимальное остовное дерево. Алгоритм Краскала.
32. Определение булевой функции. Операции над булевыми функциями.
33. Формулы логики булевых функций.
34. Равносильные преобразования формул булевых функций.
35. Двойственность. Принцип двойственности.
36. Булева алгебра (алгебра логики). Полные системы булевых функций.
37. Нормальные формы формул булевых функций.
38. Разложение булевой функции по переменным.
39. Алгоритм Квайна построения сокращенной ДНФ.
40. Алгоритм Квайна – Мак-Класки построения сокращенной ДНФ.
41. Алгоритм построения минимальной ДНФ с помощью таблицы покрытий.
42. Применение алгебры булевых функций к релейно-контактным схемам.
Список рекомендованной литературы
1. Акимов О. Е. Дискретная математика: логика, группы, графы. – М.: Лаборатория Базовых Знаний, 2001.
2. Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная математика для инженера. – М.: Энергоиздат, 1988.
3. Липский В. Комбинаторика для программистов. – М.: Мир, 1988.
4. Нефедов В. Н., Осипова В. А. Курс дискретной математики. – М.: Издательство МАИ, 1992.
5. Новиков Ф. А. Дискретная математика для программистов. – СПб.: Питер, 2002.
6. Судоплатов С. В., Овчинникова В. В. Элементы дискретной математики. – М.: ИНФРА – М, Новосибирск: Изд-во НГТУ, 2002.
Краткие сведения о математиках
Арнольд Владимир Игоревич – математик, академик Российской Академии наук.
Беллман Ричард – американский математик.
Буль Джордж (1815 – 1864) – английский математик. Основатель математической логики.
Гильберт Давид (1862 – 1943) – немецкий математик. Его исследования оказали большое влияние на развитие многих разделов математики, особенно на развитие логических основ математики.
Дейкстра Эдсгер (1930 – 2002) – голландский ученый, виднейший специалист в области программирования, лауреат премии Тьюринга.
Декарт Рене (1596 – 1650) – французский математик и философ. Впервые ввел понятия переменной, функции, системы координат на плоскости.
Кантор Георг (1845 – 1918) – немецкий математик. Разработал теорию бесконечных множеств. Идеи Кантора оказали большое влияние на развитие математики.
Колмогоров Андрей Николаевич (1903 – 19 ) – советский математик, академике АН СССР. Основополагающее значение имеют работы в области теории вероятностей. Является автором фундаментальных работ по теории множеств, теории меры, конструктивной логике, топологии, механике, теории дифференциальных уравнений, функциональному анализу.
Фибоначчи (Леонардо Пизанский) (1180 – 1240) – итальянский математик. Основные работы – трактаты об арифметике, алгебре и геометрии, которые являются первыми произведениями, содержащими задачи на приложения алгебры и геометрии.
Эйлер Леонард (1707 – 1783) – математик, физик, механик, астроном. Родился в Швейцарии, с 1726 по 1741 г. и с 1776 по 1783 г. работал в России.
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.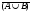 С С \ (С (AÈB))?
С С \ (С (AÈB))?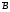 È
È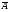 B?
B?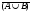 С.
С. 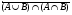 .
.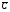 \
\ 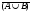 =
= 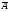 \
\ 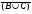 ?
?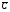 \
\ 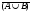 .
. 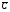 ?
?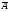 È В =
È В = 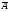
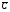 ).
).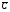 ?
?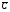 .
.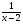 при x Î ( 3, ¥).
при x Î ( 3, ¥).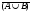 С)
С) 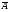
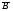 С?
С?
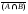 ÈС)
ÈС)  Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?
Проверить, будет ли отношение рефлексивным, симметричным, антисимметричным, транзитивным?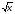 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?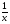 , отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?
, отображающая множество действительных чисел R во множество действительных чисел, R® R. Является ли эта функция сюръективной, инъективной, биективной? Почему?