Контрольные вопросы к теме 4
1. Выберите правильный вариант ответа 1 – 4 для следующих вопросов:
а) Сколько существует различных булевых функций n переменных? б) Сколько существует различных наборов переменных для булевой функции n переменных?
Варианты ответа: 1) 2n; 2) 22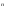 ; 3) n2; 4) n!. ; 3) n2; 4) n!.
2. Какое из следующих утверждений верно:
а) Переменные булевой функции и сама булева функция принимают значения 0 или 1;
б) Переменные булевой функции принимают значения 0 или 1, а значения самой булевой функции совпадают с множеством действительных чисел;
в) Значения переменных булевой функции совпадают с множеством действительных чисел, а сама булева функция принимает значения 0 или 1;
г) Значения переменных булевой функции и значения самой функции совпадают с множеством действительных чисел;
3. Выберите правильный вариант ответа 1 – 4 для следующих вопросов:
а) Сколько может быть различных ДНФ у булевой функции?
б) Сколько может быть различных СДНФ у булевой функции?
в) Сколько может быть различных КНФ у булевой функции?
г) Сколько может быть различных СКНФ у булевой функции?
Варианты ответа:
1 – ноль или одна; 2 – ноль или бесконечно много; 3 – ноль или одна; 4 – одна; 5 – одна или бесконечно много.
4. В какой из нормальных форм (ДНФ, СДНФ, КНФ, СКНФ) находится данная формула булевой функции трех переменных f(x, y, z):
а) xVy&z; б) x&y&z; в) (xVy)&(xVz); г) xVyVz; д) x&y&z V y&z; е) xVy; ж) x&z.
5. Какая релейно-контактная схема соответствует функции проводимости f(x) = (xVy)&(xVz)?
Ответы на контрольные вопросы
Тема 1
1. Да.
2. Если А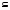 В. В.
3. Пустое множество.
4. Да. Например, множество целых чисел эквивалентно множеству четных чисел.
5. Мощность множества точек отрезка [0, 1] больше. Это множество имеет мощность континнуума, а множество натуральных чисел является счетным множеством.
Тема 2.
1. Перечислением упорядоченных пар, указанием общего свойства упорядоченных пар, матрицей бинарного отношения.
2. Рефлексивного.
3. Для симметричного.
4. Для транзитивного.
5. Например, отношение параллельности прямых есть отношение эквивалентности. Пусть x и y – углы наклона прямых x и y с осью абсцисс. Тогда отношение = {x, y x y} есть отношение частичного порядка.
6. Функция может быть задана таблицей, формулой, рекурсивной процедурой, с помощью описания.
7. б).
Тема 3.
1. б).
7. Нет. Только для неориентированного графа.
8. Нужно сложить все элементы матрицы и полученную сумму разделить на 2.
10. Нет.
11. а) и б).
12. Нет.
15. Да .
16. а), д)
17. г).
18. Нет.
19. Нет.
21. г).
22. n – 1.
23. Наименьшее – n – 1 (дерево), наибольшее – n( n – 1) 2 (полный граф).
24. Наименьшее – 0 (несвязный граф), наибольшее – n( n – 1) 2 (полный граф).
25. Нет.
27. Одну.
28. Нет.
29. Нахождение минимального пути.
30. Нахождение минимального пути.
31. Нахождение минимального остовного дерева.
32. Нахождение минимального остовного дерева.
33. Нахождение минимального остовного дерева.
34. Нахождение минимального остовного дерева.
Тема 4.
1. а)22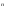 ; б) 2n. ; б) 2n.
2. а).
3. а) бесконечно много; б) ноль или одна; в) бесконечно много; г) ноль или одна.
4. а)ДНФ; б)ДНФ, СДНФ, КНФ; в)КНФ; г)ДНФ, КНФ, СКНФ; д)ДНФ; е)ДНФ, КНФ; ж)ДНФ, КНФ.
11. а) и б).
Указания к выполнению лабораторных работ
Лабораторные работы проводятся с помощью обучающей компьютерной системы "Теория графов". В лабораторных работах используются следующие разделы этой системы: "Основные понятия теории графов", "Экстремальные пути в графах".
Чтобы приступить к выполнению лабораторной работы необходимо запустить систему с помощью файла run.bat; выбрать в главном меню пункт "Обучающие программы"; указать раздел; выбрать пункт "Упражнения".
В процессе работы возможно обращение к теоретическому материалу, используя соответствующие пункты меню, а также алфавитный указатель.
Лабораторная работа №1. Основные понятия. Ориентированные графы
Для выполнения этой работы требуется изучить следующие понятия для ориентированного графа: определения дуги, пути, контура, односторонней и сильной связности, компоненты сильной связности, матриц смежности, инцидентности, сильной связности.
Лабораторная работа №2. Основные понятия. Неориентированные графы
Для выполнения этой работы требуется изучить следующие понятия для неориентированного графа: определения ребра, маршрута, цикла, связности, компоненты связности, матриц смежности, инцидентности, связности.
Лабораторная работа №3. Экстремальные пути в графах
Для выполнения этой работы требуется изучить определения нагруженного графа, минимального пути, максимального пути, кратчайшего пути, а также алгоритм Форда – Беллмана.
Контрольные задания по курсу "Дискретная математика".
1. Раздел «Множества»
Вариант № 1
1. Фирма имеет 100 предприятий, причем каждое предприятие выпускает хотя бы одну продукцию вида А, В, С. Продукцию всех трех видов выпускают 10 предприятий, продукцию А и В – 18 предприятий, продукцию А и С – 15 предприятий, продукцию В и С – 21 предприятие. Число предприятий, выпускающих продукцию А равно числу предприятий, выпускающих продукцию В и равно числу предприятий, выпускающих продукцию С. Найти число всех предприятий.
2. Упростить: 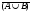 È È 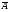 È È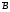 . .
3. Является ли множество А = {1, 2, 3} подмножеством множества В = {{1}, {2, 3}}?
4. Придумать пример множеств А, В, С, каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: А ÈВ = С.
5. Эквивалентны ли множества A = {x: x2 – 8x + 15= 0} и B = {2, 3}?
Вариант № 2
1. В группе спортсменов 30 человек. Из них 20 занимаются плаванием, 18 – легкой атлетикой и 10 – лыжами. Плаванием и легкой атлетикой занимаются 11 человек, плаванием и лыжами – 8, легкой атлетикой и лыжами – 6 человек. Сколько спортсменов занимаются всеми тремя видами спорта?
2. Упростить: A(AÈB).
3. В каком случае А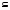 АВ? АВ?
4. Нарисовать диаграмму Эйлера-Венна для множества 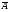 È È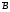 . .
5. Какое из множеств A = {1, 4, 9, 16, 25,…} и B = {1, 1/2, 1/4, 1/6, 1/8,…} имеет большую мощность?
Вариант № 3
1. В студенческой группе 20 человек. Из них 10 имеют оценку “отлично” по английскому языку, 8 - по математике, 7 - по физике, 4 - по английскому языку и по математике, 5 - по английскому языку и по физике, 4 - по математике и по физике, 3 - по английскому языку, по математике и по физике. Сколько студентов группе не имеют отличных оценок?
2. Упростить: (A\B) È (A\B).
3. Найти все подмножества множества A= {1, 2, 3, 4).
4
4. Пусть An = {0, 1/2n}. Найти U An.
n=1
5. Доказать, что множества точек контуров всех треугольников эквивалентны.
Вариант № 4
1. В классе 20 человек. На экзаменах по истории, математике и литературе 10 учеников не получили ни одной пятерки, 6 учеников получили 5 по истории, 5 – по математике и 4 – по литературе; 2 - по истории и математике, 2 - по истории и литературе, 1 - по математике и литературе. Сколько учеников получили 5 по всем предметам?
2. Упростить: (AB) È (AB).
3. Является ли множество А = {1, 2, 3} подмножеством множества В = {{1}, {2, 3}}?
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) С
5. Эквивалентны ли множества A = {2x, 0<x< ¥} и B = {2n, n = 1, 2, …}?
Вариант № 5
1. В спортивном лагере 100 человек, занимающихся плаванием, легкой атлетикой и лыжами. Из них 10 занимаются и плаванием, и легкой атлетикой, и лыжами, 18 – плаванием и легкой атлетикой, 15 – плаванием и лыжами, 21 – легкой атлетикой и лыжами. Число спортсменов, занимающихся плаванием, равно числу спортсменов, занимающихся легкой атлетикой, и равно числу спортсменов, занимающихся лыжами. Найти это число.
2. Упростить: (AÈB) È(AÈB).
3. Найти все подмножества множества A= {1, 2, 3, 4).
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) È С
5. Доказать, что множества точек контуров всех треугольников эквивалентны.
Вариант № 6
1. Группе студентов предложено три спецкурса: по мультимедиа, искусственному интеллекту и имитационному моделированию. 22 студента записались на спецкурс по мультимедиа, 18 – на спецкурс по искусственному интеллекту, 10 – на спецкурс по имитационному моделированию, 8 – на спецкурсы по мультимедиа и искусственному интеллекту, 15 – на спецкурсы по мультимедиа и имитационному моделированию, 7 – на спецкурсы по искусственному интеллекту и имитационному моделированию. 5 студентов записались на все три спецкурса. Сколько студентов в группе?
2. Верно или неверно равенство: (A \ B) È(AB) = A?
3. Придумать пример множеств А, В, С, каждое из которых имеет мощность континуума, так, чтобы выполнялось равенство: А ÈВ = С.
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) È (А \ С).
5. Эквивалентны ли множества A = {x: x2-8x+15= 0} и B = {2, 3}?
Вариант № 7
1. Во время сессии 24 студента группы должны сдать три зачета: по физике, математике и программированию. 20 студентов сдали зачет по физике, 10 – по математике, 5 – по программированию, 7 – по физике и математике, 3 – по физике и программированию, 2 – по математике и программированию. Сколько студентов сдали все три зачета?
2. Упростить: (AÈB) È (AB).
3. Доказать, что множество точек A= {(x, y): y = ½x½, -, – 1 £ x£ 1} несчетно.
4. Нарисовать диаграмму Эйлера-Венна для множества (А \ В) È С.
5. Эквивалентны ли множества A = {y: y = x3, 1< x <2} и B = {y: y = 3x, 3< x < ¥}?
Вариант № 8
В группе переводчиков 15 человек владеет английским языком, 19 – французским, 8 – немецким. 9 переводчиков владеют английским и французским языком, 7 – английским и немецким, 6 – французским и немецким. 4 переводчика владеют всеми тремя языками. Сколько переводчиков в группе?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В È С) = (А \ В) È С?
3. В каком случае А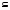 АВ? АВ?
4. Нарисовать диаграмму Эйлера-Венна для множества (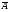 È È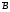 ) \ (A È B). ) \ (A È B).
5. Эквивалентны ли множества A = {x: x2 –3x + 2 = 0} и B = {1, 3}?
Вариант № 9
1. Опрос группы студентов показал, что 70% из них любят ходить в кино, 60% в театр, 30% на концерты. В кино и театр ходят 40% студентов, в кино и на концерты – 20%, в театр и на концерты – 10%. Сколько студентов (в %) ходят в кино, театр и на концерты?
2. Верно или неверно равенство: (AB) (A È В) = В?
3. Привести пример двух множеств А и В, таких, что мощность множества А больше мощности множества В.
4. Нарисовать диаграмму Эйлера-Венна для множества А \ (В С).
5. Эквивалентны ли множества A = {x: x3 – 1 = 0} и B = {x: x2 – 3x + 2 = 0}?
Вариант № 10
1. В группе 20 учеников. После медицинского осмотра на дополнительное обследование 14 учеников были направлены к терапевту, 6 – к окулисту, 5 – к ортопеду. К терапевту и окулисту были направлены 3 ученика, к терапевту и ортопеду –3, к окулисту и ортопеду – 2. Сколько учеников были направлены к терапевту, окулисту и ортопеду?
2. Упростить:  ( (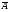 È È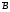 ) \ (A È B). ) \ (A È B). 
3. Нарисовать диаграмму Эйлера-Венна для множества (A B) È (C \ (A È B)).
4. Найти все подмножества множества A= {a, b, c, d}.
5. Эквивалентны ли множества A = {(x, y): y = lnx, 0 < x < ¥} и B = {(x, y): y = sinx, –¥ <x < ¥}?
Вариант № 11
1. При обследовании рынка спроса инспектор указал в опросном листе следующие данные. Из 1000 опрошенных 811 покупают жевательную резинку "Дирол", 752 – "Орбит" , 418 – "Стиморол", 570 – "Дирол" и "Орбит", 356 – "Дирол" и "Стиморол", 348 – "Орбит" и "Стиморол", 297 – все виды жевательной резинки. Показать, что инспектор ошибся.
2. Упростить: 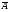 È(B \ (AÈB)). È(B \ (AÈB)).
3. Придумать пример множеств А, В, С, так, чтобы выполнялось равенство: А È В = С, причем А – конечное множество, В и С – счетные множества.
4. Нарисовать диаграмму Эйлера-Венна для множества A (B È C ) .
5. Пусть A– множество целых чисел, а B – множество четных чисел. Какие из следующих отношений справедливы: а) A=B; б) A
B; в) AÉB; г) AÊB; д) AËB; е) AÎB.
Вариант № 12
1. Всем участникам автопробега не повезло. 12 из них увязли в песке – пришлось толкать машину, 8 понадобилась замена колеса, у шестерых перегрелся мотор, пятеро и толкали машину и меняли колесо, четверо толкали машину и остужали мотор, трое меняли колесо и остужали мотор. Одному пришлось испытать все виды неполадок. Сколько было участников?
2. Пользуясь равносильными преобразованиями, установить, верно или неверно равенство: А \ (В С) = (А \В) С?
3. Доказать, что множество точек A = {y: y = 2n, n = 1, 2, …} счетно.
4. Нарисовать диаграмму Эйлера-Венна для множества (А \В) С.
5. Эквивалентны ли множества A = {(x, y): y = x3, 1< x <2} и B = {(x, y): y = 3x, 3< x < ¥}?
Вариант № 13
1. Из 10 участников ансамбля шестеро умеют играть на гитаре, пятеро – на ударных инструментах, пятеро – на духовых. Двумя инструментами владеют: гитарой и ударными – трое, ударными и духовыми – двое, гитарой и духовыми – четверо. Один человек играет на всех трех инструментах. Остальные участники ансамбля только поют. Сколько певцов в ансамбле?
2. Верно или неверно равенство: 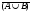 С) С) 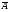 С È С È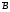 С ? С ?
3. Записать решение системы неравенств
x-2 > 0
x-5 < 0
в виде пересечения двух множеств.
4. Нарисовать диаграмму Эйлера-Венна для множества 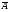 (B ÈC ) . (B ÈC ) .
5. Доказать, что множества A = {(x, y): y = x3, 1< x <2} и B = {y: y = 3x, 3< x < ¥} эквивалентны.
Вариант № 14
1. В одной студенческой группе 10 человек могут работать на Дельфи, 10 – на Паскале, 6 – на Си. По два языка знают: 6 человек – Дельфи и Паскаль, 4 – Паскаль и Си, 3 – Дельфи и Си. Один человек знает все три языка. Сколько студентов в группе?
2. Верно или неверно соотношение: A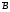 C Ì A È В? C Ì A È В?
3. Придумать пример множеств А, В, С, так, чтобы выполнялось равенство: А È В = С, причем А, В, и С – счетные множества.
4. Нарисовать диаграмму Эйлера-Венна для множества 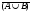 С). С).
5. Эквивалентны ли множества A = {y: y = 3x, 0<x< ¥} и B = {y: y = 3n, n = 1, 2, …}?
|
 Скачать 0.62 Mb.
Скачать 0.62 Mb.