структура капитала и дивидендная политика 6. Тема Структура капитала и дивидендная политика Цена и структура капитала
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
Цена кредиторской задолженности определяется характером выплат по каждой статье кредиторской задолженности. Поэтому необходимо рассмотреть каждую статью кредиторской задолженности. Цена кредиторской задолженности поставщикам и подрядчикам (К3) определяется прямым способом через отношение суммы штрафов и пени, уплаченных предприятием, к величине кредиторской задолженности: где df сумма штрафов, пени, уплаченных поставщикам и подрядчикам, д. е.; М1 величина кредиторской задолженности поставщикам и подрядчикам, д. е.; Т ставка налогообложения прибыли, коэфф. Поскольку согласно Налогового кодекса РФ (ст. 265) в состав внереализационных расходов входят расходы в виде штрафов, пеней и (или) иных санкций за нарушение договорных обязательств, то цена кредиторской задолженности поставщикам и подрядчикам приводится к посленалоговой базе. df отражается в форме № 2 («Расшифровка отдельных прибылей и убытков», строка 210) или определяется по данным управленческого бухгалтерского учета. Обычно К3 изменяется от 0 до 10%. Косвенный способ оценки данного вида кредиторской задолженности заключается в оценке потерь, вызванных неплатежами поставщикам. Это судебные издержки, потеря репутации, рост цен на материалы, перебои в снабжении и т. п. Оценка кредиторской задолженности этим способом не всегда поддается количественному измерению. Цена кредиторской задолженности по оплате труда (К4) определяется отношением дополнительных выплат работникам, связанных с задержками заработной платы и ее индексацией, к величине кредиторской задолженности данного вида: где dz сумма дополнительных выплат работникам, связанная с задержками заработной платы и ее индексацией, д. е.; М2 величина кредиторской задолженности по оплате труда, д. е.; Т ставка налогообложения прибыли, коэфф. Как показывает практика, данный вид кредиторской задолженности выступает самым дешевым источником финансирования, так как большинство предприятий не индексирует невыплаченную в срок заработную плату, за исключением случаев, по которым получены решения суда. Таким образом, К4 0. Цена кредиторской задолженности бюджету и внебюджетным фондам (К5) определяется величиной пени, равной 1/300 ставки рефинансирования за каждый день просрочки. Например, при ставке рефинансирования 12% годовых величина пени составит 0,04%, или в годовом исчислении 14,6%. Пени на пени не насчитываются, поэтому для определения цены кредиторской задолженности данного вида используется схема простых процентов: K5 0,04% t, (6.7) При определении налоговой базы не учитываются расходы в виде пени, штрафов и иных санкций, перечисляемых в бюджет и в государственные внебюджетные фонды (ст. 270 НК РФ), поэтому данный источник финансирования не подлежит корректировке. Важнейшей составляющей частью финансовых ресурсов, так называемой «последней линией обороны» и источником покрытия задолженности перед кредиторами является собственный капитал организации. Поскольку максимальное использование потенциальных источников финансирования присуще акционерному обществу, рассмотрим как оценивается его собственный капитал. В настоящее время в состав собственного капитала входят такие элементы, как уставный капитал, добавочный капитал, резервный фонд, фонды специального назначения, нераспределенная прибыль. Однако с позиции расчета цены капитала целесообразно выделить четыре источника собственных средств организации: привилегированные акции; обыкновенные акции; добавочный капитал; нераспределенная прибыль. Необходимо отметить, что к нераспределенной прибыли, для целей расчета цены капитала, принято относить все источники собственных средств за исключением уставного капитала. Безусловно, в таком подходе есть некоторая доля условности, поскольку, например, источники «нераспределенная прибыль» и «безвозмездно полученные средства» имеют не только различную природу и способ формирования, но и различную цену. Однако чаще всего доля безвозмездно полученных средств в структуре капитала достаточно мала, поэтому различиями можно пренебречь. Необходимость подразделения уставного капитала на два элемента (привилегированные и обыкновенные акции) состоит в том, что привилегированные акции можно рассматривать как некий гибрид, сочетающий свойства обыкновенных акций и заемного капитала. Цена выпуска привилегированных акций в качестве источника финансирования деятельности организации основана на трех факторах: 1) цена финансового актива эквивалентна сумме ожидаемых дисконтированных доходов по данному активу; 2) размер дивиденда по привилегированным акциям заранее определен; 3) срок деятельности организации не ограничен. Таким образом, цена использования данного источника финансирования представляет собой сумму бесконечно убывающей геометрической прогрессии и может быть рассчитана по формуле: где kp цена использования в качестве источника финансирования привилегированных акций, %; D величина фиксированных дивидендных выплат в каждом периоде, д. е.; Pnцена размещения привилегированных акций, д. е. Выплата и размер дивидендов по обыкновенным акциям, в отличие от привилегированных, не является юридической обязанностью компании и зависит от эффективности ее текущей деятельности и решения собрания акционеров. В связи с этим достоверное определение цены использования в качестве источника финансирования обыкновенных акций представляется наиболее сложным. Существует несколько моделей для такого расчета, наиболее известными из которых являются модель Гордона и модель CAPM. Согласно модели Гордона, цена источника средств «обыкновенные акции» (ks), можно представить как ставку дисконтирования, которая уравнивает приведенную стоимость всех ожидаемых будущих дивидендов на одну акцию и текущую рыночную цену одной акции. где P0 рыночная цена акции в момент времени 0, д. е.; Dt денежные дивиденды на одну акцию, выплата которых ожидается в конце периода времени t, д. е.; ks соответствующая ставка дисконтирования (приемлемая доходность), коэфф. Как видно из формулы (6.9), определение ставки дисконтирования, уравнивающей поток будущих дивидендов с текущей рыночной ценой акции, зависит от точности расчета потока будущих дивидендов. В этом и состоит основная трудность определения цены источника «обыкновенные акции». В зависимости от предполагаемой динамики дивидендов, конкретное представление формулы (6.9) меняется. В модели Гордона выделяются три варианта динамики прогнозных значений дивидендов: дивиденды не меняются; дивиденды возрастают с постоянным темпом прироста; дивиденды возрастают с изменяющимся темпом прироста. Если в течение всего времени выплачиваются одинаковые дивиденды, темп прироста дивидендов равен нулю, и данная модель называется моделью нулевого роста (zero-growth model). В этом случае цена использования в качестве источника финансирования обыкновенных акций определяется следующим образом: где ks цена использования в качестве источника финансирования обыкновенных акций, %; P0 рыночная цена обыкновенной акции, д. е.; D величина выплаченного дивиденда, д. е.; Во втором варианте прогнозных значений дивидендов предполагается, что выплачиваемые дивиденды растут от периода к периоду в одной пропорции и соответствующая модель называется моделью постоянного роста (constant-growth model). Эта модель предполагает, что базовая величина дивиденда (т. е. последнего выплачиваемого дивиденда) Div ежегодно увеличивается с темпом прироста g. Таким образом, текущие дивиденды представляют собой основу, на которой строится ожидаемый рост будущих дивидендов. Решая уравнение (6.9) относительно ks, учитывая постоянный темп прироста дивидендов, получаем следующую формулу для нахождения цены источника «обыкновенные акции»: где ks цена использования в качестве источника финансирования обыкновенных акций, %; P0 рыночная цена обыкновенной акции, д. е.; D0 величина последнего выплаченного дивиденда, д. е.; g прогнозируемый темп прироста дивидендов, коэфф. Однако если ожидается, что рост дивидендов в будущем прекратится, или дивиденды будут расти с непостоянным темпом, то в этом случае модель постоянного роста нельзя использовать в качестве основы для определения цены источника «обыкновенные акции». При оценке цены использования в качестве источника финансирования обыкновенных акций, дивиденды по которым возрастают с изменяющимся темпом прироста, используется модель переменного роста (multiple-growth model). Согласно формуле (6.11) цена использования в качестве источника финансирования обыкновенных акций очень чувствительна к параметру g: даже незначительное его изменение может существенно повлиять на цену. Поэтому при определении цены можно попытаться разбить интервал прогнозирования на подынтервалы, каждый из которых характеризуется собственным темпом прироста g. Так, например, если выделить два подынтервала с темпами прироста g и q соответственно, то цена источника «обыкновенные акции» можно выразить из следующей формулы: где ks цена использования в качестве источника финансирования обыкновенных акций, коэфф.; P0 рыночная цена обыкновенной акции, д. е.; D0 дивиденд, выплачиваемый в базисный момент времени, д. е.; Dl прогноз дивиденда в l-м периоде, д. е.; g прогнозируемый темп прироста дивидендов в первые l периодов, коэфф.; q прогнозируемый темп прироста дивидендов в последующие периоды, коэфф. Главная сложность применения этой модели состоит в выделении подынтервалов, прогнозировании темпов прироста (как правило, в прогнозах темпы прироста в динамике снижаются, что влияет на окончательное значение показателя цены капитала). Безусловно, модель должна рассматриваться в динамике и постоянно уточняться по мере получения новой информации, в частности, по истечении очередного подынтервала. В теории и практике оценки цены источника «обыкновенные акции» с использованием модели Гордона получила достаточно широкое распространение ситуация, когда темп прироста дивидендов в течение нескольких лет прогнозного периода меняется, однако по истечении этих лет он устанавливается на некотором постоянном уровне. Обычно такое развитие событий характерно для компаний, осваивающих новые виды продукции или перспективные рынки сбыта. Тогда в течение непродолжительного подынтервала темп прироста может быть сравнительно высоким, причем не обязательно одинаковым, а затем он снижается и становится постоянным. Предположим, что продолжительность фазы непостоянного роста составляет l лет, а дивиденды в этот период по годам равны Dn, n 1, 2, …, l; Dl 1 первый ожидаемый дивиденд фазы постоянного роста с темпом g. Графически данную ситуацию можно представить на рис. 6.2. Из приведенной схемы видно, что в первые l лет прогнозируется бессистемное изменение величины годового дивиденда, а начиная с момента (l 1), эта величина будет равномерно увеличиваться, т. е. Dl 1 Dl (1 g); Dl 2 Dl 1 (1 g) Ds (1 g)2 (6.13) и т. д. 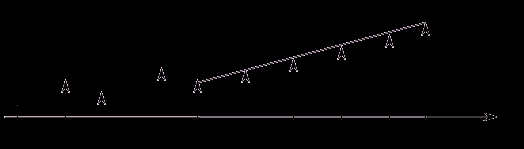 Рис. 6.2. Динамика дивидендов при выделении двух фаз изменений В этом случае базовая формула для определения цены источника «обыкновенные акции» может быть трансформирована следующим образом:  Помимо указанных недостатков, модель Гордона не учитывает фактор риска и может быть реализована лишь для компаний, выплачивающих дивиденды. В отношении обыкновенных акций определение цены капитала имеет особо важное значение, когда планируется выпуск новых акций как для финансирования новых инвестиционных программ, так и для покрытия некоторых неотложных расходов при недостаточности иных источников средств. В этом случае при оценке цены капитала источника «обыкновенные акции новой эмиссии» применяется модифицированная модель Гордона, учитывающая затраты на размещение акций:  где kcs цена источника «обыкновенные акции новой эмиссии», %; P0 рыночная цена обыкновенной акции, д. е.; D1 прогнозный дивиденд, по данной акции, д. е.; g прогнозируемый темп прироста дивидендов, коэфф.; fc уровень затрат на размещение акций в долях единицы. Выбор той или иной формулы для расчета определяется моделью дивидендной политики, используемой акционерным обществом. Вместо того, чтобы оценивать величину будущего потока дивидендов акционерного общества, а затем вычислять цену источника «обыкновенные акции», эту задачу можно решить непосредственно, оценив требуемую ставку доходности обыкновенных акций компании, с помощью модели CAPM, которая в известной степени лишена недостатков, присущих модели Гордона. Однако, несмотря на то, что она основывается на нескольких нереалистических предположениях таких, как: эффективность рынков капитала, т. е. все инвесторы хорошо информированы; трансакционные издержки достаточно малы; инвесторы принимают цену как экзогенно заданную величину, т. е. ни один из инвесторов не располагает достаточным количеством средств, чтобы повлиять на рыночную цену акции и др.; и поэтому не может быть проверена эмпирически, тем не менее, она довольно часто используется в процессе оценки цены капитала, благодаря своей логической привлекательности. Согласно этой модели, цена собственного капитала рассчитывается следующим образом: ks rf (rm rf) j , (6.16) где ks цена использования в качестве источника финансирования обыкновенных акций, %; rm доходность финансового рынка в целом, коэфф.; rf доходность вложения в безрисковые активы, коэфф.; j коэффициент систематического риска актива, определяется для каждой конкретной акции на основе статистических данных фондового рынка. Для применения этого подхода на практике необходимо иметь следующую информацию о рынке ценных бумаг: доходность вложения в безрисковые активы, премия за риск, j коэффициенты. При чем очень важно, чтобы все показатели, фигурирующие в уравнении (6.16), оказались спрогнозированными как можно более качественно. Как видно из формулы (6.16), на основе доходности финансового рынка в целом, определяется премия за риск как разность между доходностью финансового рынка в целом и доходностью вложения в безрисковые активы. Рыночная премия за риск может быть рассчитана на основе: ex post, или фактической доходности; ex ante, или ожидаемой доходности. Ex post премия за риск представляет собой всеобъемлющий детализированный анализ фактических данных о премии за риск на основе статистической информации за длительные периоды, используемой для расчета среднегодовой доходности различных ценных бумаг. Однако этот подход следует применять в анализе лишь с надлежащей интерпретацией, поскольку изменение анализируемого периода может значительно повлиять на результаты исследования. Осознание спорности предпосылки о том, что прогнозируемые оценки должны основываться на экстраполяции статистических данных, нередко являющихся бессмысленными с позиции здравого смысла, привело к появлению подхода, в основе которого заложена ex ante премия за риск. Данный подход представляет оценки годовой доходности, рассчитанные на ближайшее будущее. Обычно он опирается на значения мировых индексов, так в США это индекс S&P 500, и представляет собой согласованные оценки финансовых аналитиков, экономистов и прочих специалистов. Наиболее простой метод расчета ожидаемых значений премии за риск заключается в использовании модели дисконтирования денежного потока для оценки ожидаемой рыночной доходности. Этот подход основывается на предпосылке, что при условии равновесия рынка капитала значения ожидаемой и требуемой доходности рыночного портфеля совпадают. где P0 рыночная цена портфеля, д. е.; D1 прогнозный дивиденд по рыночному портфелю, д. е.; rm требуемая доходность рыночного портфеля, коэфф.; rf доходность вложения в безрисковые активы, коэфф.; RPm рыночная премия за риск, коэфф.; g средний ожидаемый долгосрочный темп роста рыночного индекса, коэфф. Поскольку значение показателя D1 для рыночного портфеля, представленного каким-либо биржевым индексом, может быть предсказано довольно точно и, кроме того, текущее рыночное значение индекса, используемого для вычисления P0, также известно, основной задачей является оценка g. В этом случае при расчете рыночной премии за риск задача прогнозирования упрощается, поскольку предположение о постоянном долгосрочном темпе роста доходности портфеля «зрелых» акций, например, такого как S&P 500, более обосновано, чем в отношении какой-то конкретной акции. При использовании в анализе информации, предоставляемой финансовыми аналитиками, экономистами и прочими специалистами в этой области, может возникнуть такая проблема как значительные различия в прогнозах будущей доходности. Для выхода из подобной ситуации было бы разумно использовать среднее значение, полученное из нескольких прогнозов Для расчета цены источника «обыкновенные акции» с помощью модели CAPM также необходимо определить значение -коэффициента, который характеризует меру изменчивости акции относительно некой средней акции, а его значения можно найти из уравнения характеристической линии акции, представляющей собой линейную регрессию между прошлой доходностью данной акции и прошлой рыночной доходностью, оцениваемой некоторым общепринятым индексом. Это исторические или фактические значения . Исторические отражают степень рискованности акций, в прошлом и в этом случае предполагается, что риск компании в прошлом равен будущему риску. Однако, для отдельных фирм прошлая и будущая оценки риска часто не совпадают, в результате чего может наблюдаться значительное колебание -коэффициентов во времени. Поэтому нужно иметь в виду следующие моменты. 1. Расчет может быть основан на временных периодах различной длительности (год три и т. д.). 2. Доходность может исчисляться по разным периодам владения: за день, неделю, месяц, квартал, год и т. д. 3. Очень важное значение имеет выбор индекса, так как его значение может существенно повлиять на вычисление . Чем «шире» индекс, тем точнее -коэффициент. Таким образом, желательно, чтобы индекс включал данные о доходности всех активов и инструментов акций, облигаций, аренды, недвижимости и т. д. Представленные методы определения цены источника «обыкновенные акции» нельзя рассматривать как исключающие друг друга. Ни один из них не превалирует над другим, и все они не исключают ошибки при практическом применении. Поэтому при исчислении цены источника финансирования «обыкновенные акции» эти методы необходимо применять параллельно, выбирая тот результат, который дает наиболее достоверный показатель в каждом конкретном случае. Поскольку акции большинства российских эмитентов не обращаются на открытом рынке, то цена уставного капитала будет определяться исходя из ставки дивиденда и номинальной цены определенного вида или типа акции: где ks цена использования в качестве источника финансирования обыкновенных акций, %; D величина выплаченного дивиденда по определенному виду или типу акций, д. е.; N номинальная цена определенного вида или типа акций, д. е. Если же акционерное общество не выплачивает дивидендов по обыкновенным акциям, что является наиболее распространенной практикой в России, то цена данного источника финансирования будет равна нулю, а цена всего уставного капитала ставке дивиденда по привилегированным акциям, в результате чего цена уставного капитала будет стремиться к минимуму. Российская практика показывает, что добавочный капитал организаций, образованный за счет переоценки основных фондов, в несколько раз превышает уставный. Формально по нему нет дивидендных выплат, но фактически, если предприятие создавалось бы в текущий момент, то акционерам пришлось бы вложить сумму, равную уставному и добавочному капиталу по действующему балансу. Поэтому для оценки добавочного капитала необходимо использовать ту норму прибыли, которую акционеры считают приемлемой для инвестирования в данное предприятие. В основе оценки цены использования в качестве источника финансирования нераспределенной прибыли заложен принцип альтернативных затрат, суть которого заключается в следующем: во-первых, собственники, отказываясь от некоторой части дивидендов и направляя их на расширение деятельности предприятия, рассчитывают получить некоторое вознаграждение, а, во-вторых, размер ожидаемого вознаграждения должен обеспечить норму прибыли, не менее, чем по обыкновенным акциям (в противном случае, с позиции эффективности собственникам организации следует изъять дивиденды в полном объеме и разместить полученные ресурсы в активы, обеспечивающие более высокую доходность). Таким образом, цена использования в качестве источника финансирования нераспределенной прибыли (krp) примерно равна цене источника финансирования «обыкновенные акции», однако в отдельных случаях может быть ниже, поскольку эмиссия ценных бумаг всегда несет за собой дополнительные расходы. Обыкновенные акции это достаточно дорогой источник финансирования, поскольку они являются одними из самых рискованных ценных бумаг и, следовательно, должны приносить более высокий доход своим держателям. Кроме того, при размещении новых выпусков акций акционерное общество несет дополнительные затраты, связанные с мониторингом фондового рынка, оплатой услуг финансовых посредников, печатанием бланков ценных бумаг и т. п. Поэтому цена вновь выпущенной обыкновенной акции (Кe) определяется по формуле: где D1 величина дивиденда по обыкновенной акции, д. е.; Р0 рыночная цена обыкновенной акции, д. е.; F затраты на размещение нового выпуска акций относительно их рыночной цены, коэфф.; g прогнозируемый темп прироста дивидендов, коэфф. Таким образом, Р0 (1 F) чистая цена за новый выпуск акций, полученная акционерным обществом. Исходя из определения цены капитала, как относительной величины затрат, которые несет предприятие за привлечение финансовых ресурсов из различных источников, можно рассчитать цену капиталапо формуле среднеарифметической взвешенной: где WACC цена капитала, %; Кi цена i-го источника финансирования, %; di удельный вес i-го источника в структуре пассивов, коэфф.; i порядковый номер источника финансирования; n общее количество используемых предприятием источников финансирования. Для нормального функционирования организации в долгосрочной перспективе необходимо, чтобы отдача от используемого капитала (норма чистой прибыли по капиталу) была больше, чем его цена. Другими словами, организация должна получать больше, чем платить за привлеченный капитал. Поэтому она может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя WACC. С ним сравнивается показатель IRR конкретного инвестиционного проекта. Если IRR WACC, то проект следует принять, если IRR WACC, то проект следует отвергнуть. Если компания, в силу каких-либо долгосрочных перспектив, все-таки принимает инвестиционное решение по второму варианту, то это приведет к снижению рыночной стоимости предприятия, поскольку часть прибыли будет неизбежно расходоваться на «доплату» кредиторам или акционерам. |
