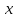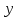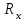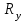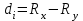295317 5 в-т ст-ка. Тема Выборочное наблюдение 3
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
Тема 9 «Непараметрические методы»Задача 1. Рассчитать коэффициенты ассоциации и контингенции. Коэффициенты ассоциации и контингенции служат для определения тесноты связи между качественными признаками, если размерность задачи не превышает двух параметров на двух уровнях. Исходные данные для расчета таких коэффициентов приведено в виде таблицы сопряженности 1. Таблица 1 - Зависимость степени удовлетворенности работой молодых специалистов от уровня полученного образования
Коэффициент ассоциации 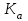 определяется по формуле: определяется по формуле: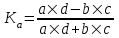 (1) (1)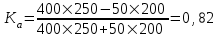 Коэффициент контингенции 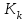 определяется по формуле: определяется по формуле: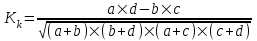 (2) (2)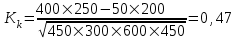 Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если 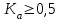 или или 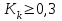 . .Расчет коэффициентов ассоциации и контингенции выявил умеренную ( 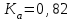 и и 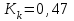 ) подтвержденную ( ) подтвержденную (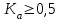 и и 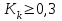 ) зависимость степени удовлетворенности работой молодых специалистов от уровня полученного образования. ) зависимость степени удовлетворенности работой молодых специалистов от уровня полученного образования.Задача 2. Рассчитать коэффициенты взаимной сопряженности Чупрова и Пирсона. В случае, когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряженности Пирсона и Чупрова. Исходные данные для расчета таких коэффициентов приведено в виде таблицы сопряженности 2. Таблица 2 - Зависимость взаимоотношений сотрудников в коллективе от условий производства
Коэффициент Пирсона 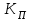 определяется по формуле: определяется по формуле: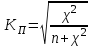 , (3) , (3)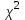 - критерий Пирсона; - критерий Пирсона;  - количество наблюдений. - количество наблюдений.Критерий Пирсона определяется по формуле: 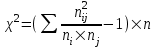 , (4) , (4)где 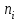 – суммы показателей по i-той строке; – суммы показателей по i-той строке; 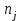 - суммы показателей по j-тому столбцу; - суммы показателей по j-тому столбцу; 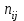 j - показатель, находящийся на пересечении i-той строки и j-того столбца. j - показатель, находящийся на пересечении i-той строки и j-того столбца.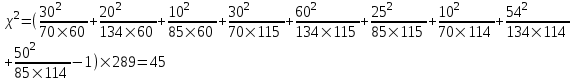 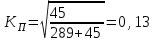 Коэффициент Чупрова 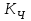 определяется по формуле: определяется по формуле: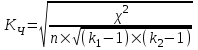 , (5) , (5)где 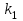 - число строк в таблице; - число строк в таблице; 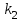 - число граф в таблице. - число граф в таблице.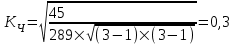 Методика анализа наличия связи с использованием коэффициентов Пирсона и Чупрова заключается в следующем: чем ближе значения 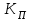 и и 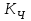 к 1, тем теснее связь; к 1, тем теснее связь;если 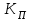 0,3 и 0,3 и 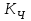 0,3, то связь имеется и наоборот; 0,3, то связь имеется и наоборот;если 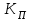 0,3 и 0,3 и 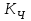 0,3 - ориентируемся на значение 0,3 - ориентируемся на значение 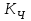 , так как он учитывает размерность таблицы и более точен. , так как он учитывает размерность таблицы и более точен.Расчет коэффициентов Пирсона и Чупрова выявил достаточно ckf,e. ( 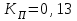 и и 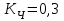 ) неподтвержденную ( ) неподтвержденную (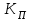 < 0,3 и < 0,3 и 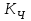 0,3) зависимость взаимоотношений сотрудников в коллективе от условий производства. 0,3) зависимость взаимоотношений сотрудников в коллективе от условий производства.Задача 3. Рассчитать коэффициент корреляции Спирмена. Исходные данные для расчета коэффициента Спирмена приведены в таблице 3. Таблица 3 - Зависимость предпочтений в выборе телепередач для просмотра от уровня среднедушевого дохода
Коэффициент корреляции Спирмена 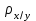 рассчитывается по формуле: рассчитывается по формуле: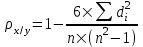 , (6) , (6)где 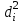 - квадрат разности рангов; n - число пар рангов. - квадрат разности рангов; n - число пар рангов.Ранжирование - это процедура упорядочения объектов изучения, которая выполняется на основе признака предпочтения. Процесс ранжирования исходных данных показан в таблице 4. Таблица 4 – К расчету коэффициента корреляции Спирмена
Продолжение таблицы 4
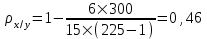 Связь между признаками можно признать статистически значимой, если значение 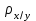 > 0,5. > 0,5.Расчет коэффициента корреляции Спирмена выявил близкую к умеренной ( 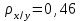 ), но статистически не значимую ( ), но статистически не значимую (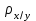 < 0,5) зависимость предпочтений в выборе телепередач для просмотра от уровня среднедушевого дохода населения. < 0,5) зависимость предпочтений в выборе телепередач для просмотра от уровня среднедушевого дохода населения.Задача 4. Рассчитать множественный коэффициента корреляции Кендела. Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции Кендела. Результаты работы экспертной группы для расчета коэффициента конкордации приведены в таблице 5. Таблица 5 – Ранжирование характеристик информации группой экспертов
Коэффициент Кендела 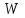 определяется по формуле: определяется по формуле: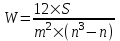 , (7) , (7)где 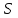 – отклонение суммы квадратов рангов от средней квадратов рангов; – отклонение суммы квадратов рангов от средней квадратов рангов; 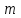 – количество факторов; – количество факторов;  – число наблюдений. – число наблюдений.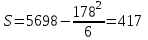 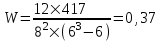 Значимость 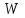 проверяется на основе проверяется на основе 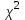 . Расчетное значение критерия Пирсона . Расчетное значение критерия Пирсона 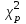 определяется по формуле: определяется по формуле: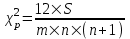 (8) (8)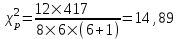 Табличное значение критерия Пирсона 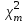 определяется по статистическим таблицам. При уровне значимости определяется по статистическим таблицам. При уровне значимости 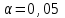 и числе степеней свободы и числе степеней свободы 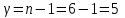 значение значение 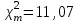 . .Расчет коэффициента корреляции Кендела выявил умеренную ( 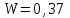 ) статистически значимую ( ) статистически значимую (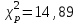 больше больше 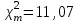 ) согласованность мнений экспертов относительно важности характеристик информации. ) согласованность мнений экспертов относительно важности характеристик информации. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

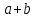 = 450
= 450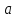 = 400
= 400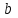 = 50
= 50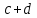 = 450
= 450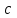 = 200
= 200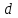 = 250
= 250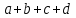 = 900
= 900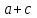 = 600
= 600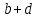 = 300
= 300