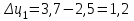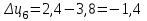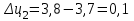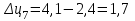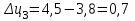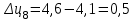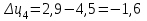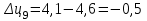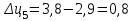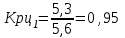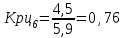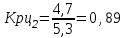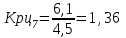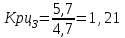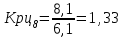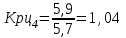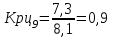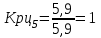295317 5 в-т ст-ка. Тема Выборочное наблюдение 3
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
Тема 10 «Ряды динамики»Задача 1. Спрогнозировать развитие социально-экономического явления с использованием среднего абсолютного прироста. Ряд динамики – это ряд изменяющихся во времени значений статистического показателя, расположенного в хронологическом порядке. Интервальный ряд динамики для прогнозирования разводимости по Валинскому району Пензенской области на основе среднего абсолютного прироста представлен в таблице 1. Таблица 1 - Общие коэффициенты разводимости по Валинскому району Пензенской области (на 1000 чел. населения)
Прогнозирование инерционного ряда динамики предполагает, что закономерность развития, действующая в прошлом, сохранится и в будущем, т. е. прогноз основан на экстраполяции. Прогнозирование по среднему абсолютному приросту применяется, когда общая тенденция ряда динамики линейна. Метод основан на предположении о равномерном изменении уровней ряда, т.е. о стабильности абсолютных приростов. В таком случае экстраполяция осуществляется по зависимости: 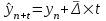 , (1) , (1)где 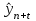 – прогнозируемый уровень ряда динамики на – прогнозируемый уровень ряда динамики на 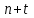 период; период; 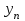 – последний – последний  -й уровень ряда динамики в исследуемом периоде; -й уровень ряда динамики в исследуемом периоде; 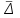 - средний абсолютный прирост уровней ряда динамики за исследуемый период; - средний абсолютный прирост уровней ряда динамики за исследуемый период; 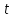 – срок прогноза. – срок прогноза.Средний абсолютный прирост уровней ряда динамики определяется по формуле: 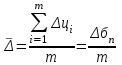 , (2) , (2)где 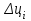 - абсолютный цепной прирост уровней ряда динамики в - абсолютный цепной прирост уровней ряда динамики в  -м периоде времени; -м периоде времени; 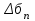 - абсолютный базисный прирост уровней ряда динамики в последнем - абсолютный базисный прирост уровней ряда динамики в последнем  -м периоде времени; -м периоде времени; 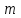 – число цепных абсолютных приростов уровней в ряду динамики. – число цепных абсолютных приростов уровней в ряду динамики.Цепной абсолютный прирост уровней ряда динамики определяется по формуле: 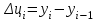 , (3) , (3)где 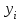 - уровень ряда динамики сравниваемого - уровень ряда динамики сравниваемого  -го периода; -го периода; 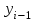 - уровень ряда динамики предшествующего - уровень ряда динамики предшествующего 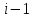 -го периода. -го периода.Базисный абсолютный прирост уровней ряда динамики определяется по формуле: 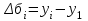 , (4) , (4)где 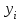 - уровень ряда динамики сравниваемого - уровень ряда динамики сравниваемого  -го периода; -го периода; 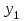 - уровень ряда динамики первого в ряду периода. - уровень ряда динамики первого в ряду периода.Рассчитаем цепные абсолютные приросты уровней ряда динамики:
Рассчитаем базисный абсолютный прирост уровней ряда динамики: 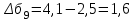 Рассчитаем средний абсолютный прирост уровней ряда динамики: 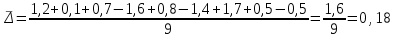 Спрогнозируем уровни ряда динамики на последующие 2 периода времени с использованием среднего абсолютного прироста: 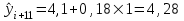 ‰ ‰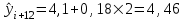 ‰ ‰Задача 2. Спрогнозировать развитие социально-экономического явления с использованием среднего темпа роста. Интервальный ряд динамики для прогнозирования брачности по Валинскому району Пензенской области на основе среднего темпа роста представлен в таблице 2. Таблица 2 – Общие коэффициенты брачности по Валинскому району Пензенской области (на 1000 чел. населения)
Прогнозирование по среднему темпу роста осуществляется, когда общая тенденция ряда динамики экспоненциальна. В таком случае экстраполяция осуществляется по зависимости: 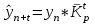 , (5) , (5)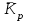 - средний коэффициент роста уровней ряда динамики за исследуемый период. - средний коэффициент роста уровней ряда динамики за исследуемый период.Средний коэффициент роста уровней ряда динамики определяется по формуле: 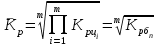 , (6) , (6)где 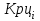 - цепной коэффициент роста уровней ряда динамики в - цепной коэффициент роста уровней ряда динамики в  -м периоде времени; -м периоде времени; 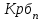 - базисный коэффициент роста уровней ряда динамики в последнем - базисный коэффициент роста уровней ряда динамики в последнем  -м периоде времени; -м периоде времени; 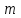 – число цепных коэффициентов роста уровней в ряду динамики. – число цепных коэффициентов роста уровней в ряду динамики.Цепной коэффициент роста уровней ряда динамики определяется по формуле: 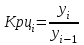 (7) (7)Базисный коэффициент роста уровней ряда динамики определяется по формуле: 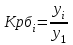 (8) (8)Рассчитаем цепные коэффициенты роста уровней ряда динамики:
Рассчитаем базисный коэффициент роста уровней ряда динамики: 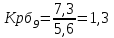 Рассчитаем средний коэффициент роста уровней ряда динамики: 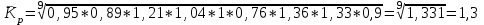 Спрогнозируем уровни ряда динамик на последующие 2 периода времени с использованием среднего коэффициента роста: 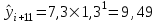 ‰ ‰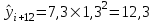 ‰ ‰ |