295317 5 в-т ст-ка. Тема Выборочное наблюдение 3
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
Тема 6 «Корреляционный анализ»Задача 1. Рассчитать линейный коэффициент корреляции. Корреляционный анализ направлен на измерение тесноты и направления связи между факторным ( 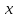 ) и результативным ( ) и результативным (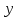 ) признаками. Количественно оценить тесноту и направление связи между двумя признаками при парной корреляции в случае наличия между ними линейной зависимости можно посредством расчета линейного коэффициента корреляции. ) признаками. Количественно оценить тесноту и направление связи между двумя признаками при парной корреляции в случае наличия между ними линейной зависимости можно посредством расчета линейного коэффициента корреляции.Исходные данные, распределение которых близко к нормальному, для расчета линейной коэффициента корреляции приведены в таблице 1. Таблица 1 – Исходные данные
Линейный коэффициент корреляции 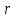 определяется по формуле: определяется по формуле: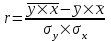 , (1) , (1)где 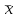 - среднее значение факторного признака; - среднее значение факторного признака; 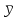 - среднее значение результативного признака; - среднее значение результативного признака; 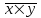 - среднее значение из произведений средних величин факторного и результативного признака; - среднее значение из произведений средних величин факторного и результативного признака; 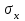 - среднее квадратическое отклонение факторного признака; - среднее квадратическое отклонение факторного признака; 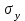 - среднее квадратическое отклонение результативного признака. - среднее квадратическое отклонение результативного признака.Для удобства промежуточных расчетов перестроим таблицу 1 в таблицу 2. Таблица 2 – К расчету линейного коэффициента корреляции
Среднее значение результативного признака определяется по формуле: 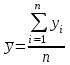 , (2) , (2)где  - объем статистической совокупности. - объем статистической совокупности.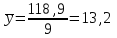 млрд. руб. млрд. руб.Среднее значение факторного признака определяется по формуле: 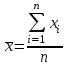 (3) (3)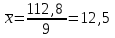 млрд. руб. млрд. руб.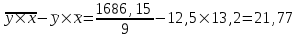 млрд. руб. млрд. руб.Среднее квадратическое отклонение результативного признака определяется по формуле: 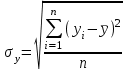 (4) (4)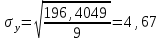 Среднее квадратическое отклонение факторного признака определяется по формуле: 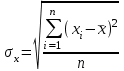 (5) (5)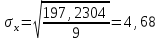 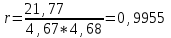 Интерпретацию значения линейного коэффициента корреляции проведем в соответствии с критериями оценки тесноты связи, приведенными в таблице 3. Таблица 3 - Количественные критерии оценки тесноты связи
Поскольку 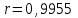 входит в диапазон значений от ± 0,7, до ± 1, то можно утверждать, что связь между доходами консолидированного бюджета субъектов РФ и расходами консолидированного бюджета субъектов РФ сильная. входит в диапазон значений от ± 0,7, до ± 1, то можно утверждать, что связь между доходами консолидированного бюджета субъектов РФ и расходами консолидированного бюджета субъектов РФ сильная.Задача 2. Определить значимость коэффициента корреляции (воспользоваться функцией СТЬЮДЕНТ.ОБР.2Х). Значимость линейного коэффициента корреляции проверяется с помощью t – критерия Стьюдента. При этом выдвигается и проверяется нулевая гипотеза (Но) о равенстве коэффициента корреляции нулю [Н0: r = 0]. При проверке этой гипотезы используется t – статистика: 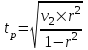 , (6) , (6)где 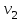 - число степеней свободы. - число степеней свободы.Число степеней свободы характеризует число свободно варьирующих элементов совокупности и определяется по формуле: 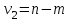 , (7) , (7)где 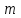 - количество параметров уравнения регрессии ( - количество параметров уравнения регрессии (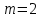 ). ).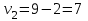 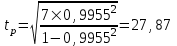 Критическое значение критерия Стьюдента 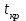 можно определить с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х табличного процессора MS Excel. можно определить с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х табличного процессора MS Excel.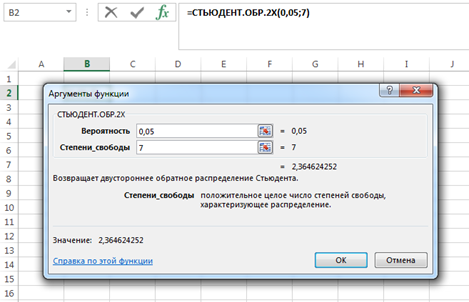 Рисунок 1 – Определение 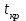 с помощью СТЬЮДЕНТ.ОБР.2Х с помощью СТЬЮДЕНТ.ОБР.2ХТаким образом, при уровне значимости 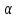 = 0,05 и числе степеней свободы = 0,05 и числе степеней свободы 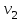 = 7 критическое значение критерия Стьюдента = 7 критическое значение критерия Стьюдента 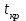 = 2,36. = 2,36.Так как 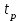 (27,87) > (27,87) > 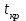 (2,36), то гипотеза Н0 отвергается, что свидетельствует о значимости линейного коэффициента корреляции, т.е. о статистической существенности зависимости между факторным и результативным признаком в совокупности. (2,36), то гипотеза Н0 отвергается, что свидетельствует о значимости линейного коэффициента корреляции, т.е. о статистической существенности зависимости между факторным и результативным признаком в совокупности. |

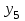 ,
, ,
,