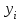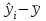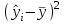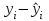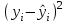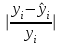295317 5 в-т ст-ка. Тема Выборочное наблюдение 3
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
Тема 7 «Регрессионный анализ»Задача 1. Рассчитать параметры уравнения парной линейной регрессии. Регрессионный анализ заключается в определении аналитического выражения связи между факторными и результативным признаками. Линейная связь между факторным ( 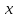 ) и результативным ( ) и результативным (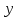 ) признаками является парной линейной регрессией. Исходные данные для построения парной линейной регрессии приведены в таблице 1. ) признаками является парной линейной регрессией. Исходные данные для построения парной линейной регрессии приведены в таблице 1.Таблица 1 – Исходные данные
Парная линейная регрессия описывается линейной функцией вида: 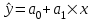 (1) (1)Оценка параметров уравнений регрессии 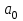 и и 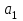 производится решением системы нормальных уравнений методом наименьших квадратов: производится решением системы нормальных уравнений методом наименьших квадратов: 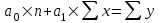 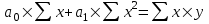 , (2) , (2)где n – объем исследуемой совокупности. Для решения системы нормальных уравнений приведем данные таблицы 1 к виду таблицы 2. Таблица 2 – К расчету коэффициентов парной линейной регрессии
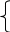 Тогда система нормальных уравнений приобретает вид: Тогда система нормальных уравнений приобретает вид: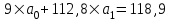 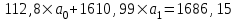 Выводя из первого уравнения 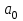 и подставляя полученное выражение во второе уравнение, получим: и подставляя полученное выражение во второе уравнение, получим: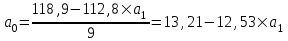 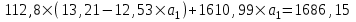 Производя почленное умножение и раскрывая скобки, получим: 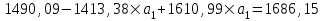 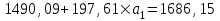 Откуда: 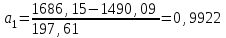 Тогда: 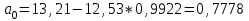 Окончательно уравнение парной линейной регрессии, связывающее размер годового оборота розничной торговли ( 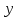 ) со среднегодовой численностью экономически активного населения территории ( ) со среднегодовой численностью экономически активного населения территории (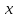 ) имеет вид: ) имеет вид: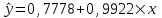 (3) (3)Задача 2. Определить статистическую значимость параметра уравнения регрессии. Оценка адекватности модели линейного уравнения парной регрессии начинается с проверки значимости коэффициента регрессии 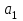 с помощью t - критерия Стьюдента: с помощью t - критерия Стьюдента: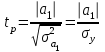 , (4) , (4)где  - дисперсия коэффициента парной линейной регрессии. - дисперсия коэффициента парной линейной регрессии.Параметр уравнения регрессии  признается статически значимым, если выполняется условие: признается статически значимым, если выполняется условие: > > 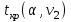 , (5) , (5)где 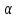 - уровень значимости; - уровень значимости; 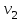 - число степеней свободы. - число степеней свободы.Число степеней свободы характеризует число свободно варьирующих элементов совокупности и определяется по формуле: 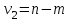 , (6) , (6)где 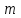 - количество параметров уравнения регрессии. - количество параметров уравнения регрессии.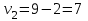 Значение 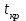 может быть определено с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х табличного процессора MS Excel. может быть определено с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х табличного процессора MS Excel.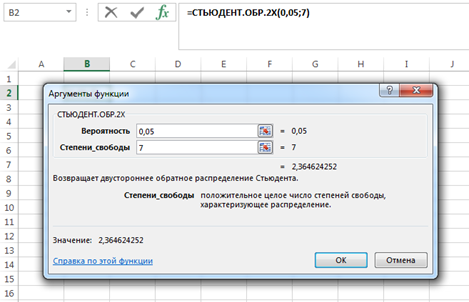 Рисунок 1 – Определение 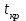 с помощью СТЬЮДЕНТ.ОБР.2Х с помощью СТЬЮДЕНТ.ОБР.2ХТаким образом, при 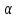 = 0,05 и = 0,05 и 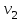 = 7 значение = 7 значение 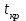 = 2,36. = 2,36.Дисперсию 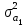 приближенно можно определить по зависимости: приближенно можно определить по зависимости: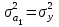 , (7) , (7)где 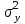 - дисперсия результативного признака в совокупности. - дисперсия результативного признака в совокупности.Значение дисперсии 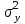 рассчитывается по формуле: рассчитывается по формуле: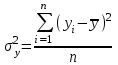 , (8) , (8)где 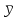 - среднее значение результативного признака в совокупности. - среднее значение результативного признака в совокупности.Значение дисперсии 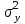 можно определить с помощью стандартной статистической функции ДИСП.Г табличного процессора Excel: можно определить с помощью стандартной статистической функции ДИСП.Г табличного процессора Excel: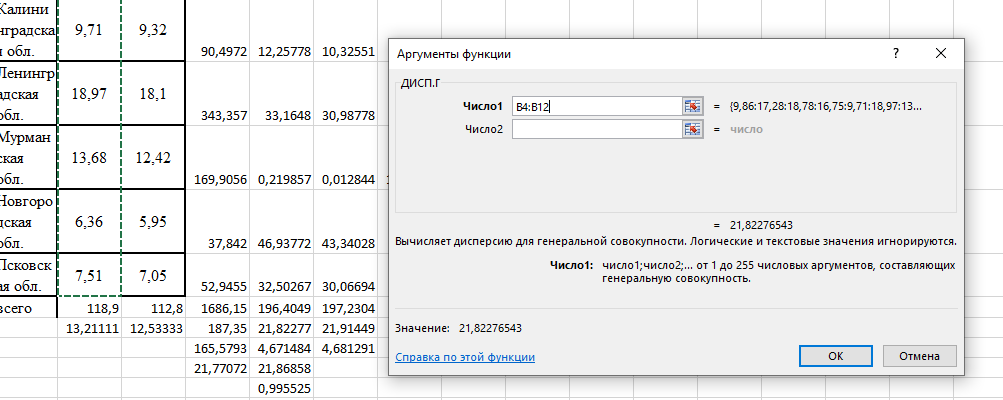 Рисунок 3 - Расчет дисперсии результативного признака с помощью ДИСП.Г Таким образом, 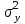 = 21,82. = 21,82.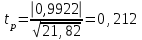 Так как 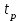 (0,212) < (0,212) < 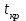 (2,36), то параметр уравнения регрессии (2,36), то параметр уравнения регрессии 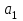 статистически не значим. статистически не значим.Задача 3. Оценить с помощью F-критерия Фишера адекватность полученного уравнения регрессии. Проверка адекватности уравнения парной линейной регрессии в целом осуществляется с помощью расчета F - критерия Фишера. Расчетное значение критерия Фишера 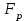 определяется по зависимости: определяется по зависимости: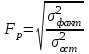 , (9) , (9)где 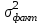 - факторная дисперсия; - факторная дисперсия; 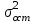 - остаточная дисперсия. - остаточная дисперсия.Факторная дисперсия 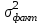 рассчитывается по формуле: рассчитывается по формуле: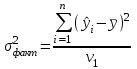 , (9) , (9)где 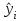 - значение результативного признака, рассчитанное по линейному уравнению регрессии; - значение результативного признака, рассчитанное по линейному уравнению регрессии; 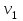 - число степеней свободы. - число степеней свободы.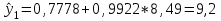 млрд. руб. млрд. руб.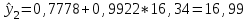 млрд. руб. млрд. руб.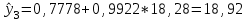 млрд. руб. и т.д. млрд. руб. и т.д.Среднее значение результативного признака определяется по формуле: 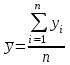 (10) (10)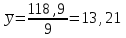 млрд. руб. млрд. руб.Число степеней свободы 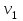 определяется по формуле: определяется по формуле: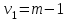 (11) (11)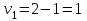 Остаточная дисперсия 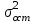 рассчитывается по формуле: рассчитывается по формуле: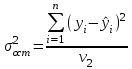 (12) (12)Для определения расчетного значения критерия Фишера, средней ошибки аппроксимации и коэффициента эластичности построим таблицу 3. Таблица 3 – К расчету F-критерия Фишера, средней ошибки аппроксимации и коэффициента эластичности
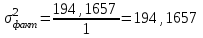 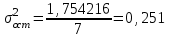 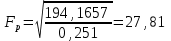 К 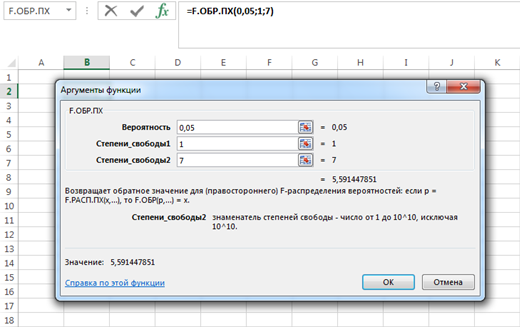 ритическое значение критерия Фишера ритическое значение критерия Фишера 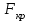 может быть определено с помощью статистической функции F.ОБР.ПХ табличного процессора MS Excel. может быть определено с помощью статистической функции F.ОБР.ПХ табличного процессора MS Excel.Рисунок 1 – Определение 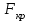 с помощью F.ОБР.ПХ с помощью F.ОБР.ПХТаким образом, при 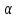 = 0,05, = 0,05, 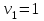 и и 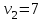 значение значение 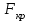 = 5,6. = 5,6.Так как 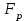 (27,81) > (27,81) > 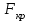 (5,6), то гипотеза о несоответствии заложенных в уравнении регрессии связей реально существующим H0 отвергается. (5,6), то гипотеза о несоответствии заложенных в уравнении регрессии связей реально существующим H0 отвергается.Задача 4. Определить среднюю ошибку аппроксимации. Значение средней ошибки аппроксимации 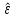 определяется по зависимости: определяется по зависимости: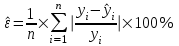 (13) (13)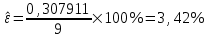 Значение средней ошибки аппроксимации не должно превышать 12 - 15%. Задача 5. На основе использования коэффициента эластичности выполнить количественную оценку влияния факторного признака на результативный. Коэффициент эластичности 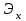 рассчитывается по формуле: рассчитывается по формуле: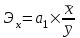 , (14) , (14)где 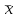 - среднее значение факторного признака в совокупности. - среднее значение факторного признака в совокупности.Среднее значение факторного признака определяется по формуле: 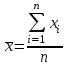 (15) (15)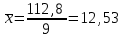 млн. чел. млн. чел.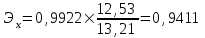 Коэффициент эластичностипоказывает, на сколько процентов в среднем изменится значение результативного при изменении факторного признака на 1%. |

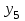 ,
,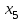 ,
,