семестровая работа (очная форма)). Теория вероятностей методические указания и варианты заданий типового расчёта

• Название: Теория вероятностей методические указания и варианты заданий типового расчёта
• Анкор: семестровая работа (очная форма)).doc
• Дата: 02.04.2018
• Размер: 484.5 Kb.
• Имя файла: семестровая работа (очная форма)).doc
• Тип: Методические указания; #17519
• страница: 6 из 13

ВАРИАНТ 12

1. Владелец одной карточки лотереи «Спортлото» (6 из 49) зачёркивает 6 номеров. Какова вероятность того, что им будет угадано 5 номеров в очередном тираже?

2. На 30 одинаковых жетонах написано 30 двузначных чисел от 11 до 40. Жетоны помещены в пакет и тщательно перемешены. Какова вероятность вынуть жетон с номером, кратным 3 или 2?

3. Произведён залп из двух орудий по мишени. Вероятность попадания из первого орудия равна 0,85, из второго 0,91. Найти вероятность поражения цели.

4. Рабочий обслуживает 3 станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго 0,3, для третьего 0,04. Обработанные детали откладываются в один ящик. Производительность первого станка в три раза больше, чем второго; а третьего в два раза меньше, чем второго. Определить вероятность того, что взятая на удачу деталь будет бракованной.

5. Имеются 10 одинаковых по виду урн, из которых в 9 находятся по 2 чёрных и 2 белых шара, а в одной 5 белых и 1 чёрный шар. Из наугад взятой урны извлечён шар. Чему равна вероятность того, что этот шар взят из урны, содержащей 5 белых шаров, если он оказался белый?

6. Агентство по страхованию автомобилей разделяет водителей по 3 классам: класс H₁ (мало рискует), класс Н₂ (рискует средне), Н₃ (сильно рискует). Агентство предполагает, что из всех водителей, застраховавших автомобили, 30 % принадлежат к классу Н₁ 50 % к классу Н₂, 20 % к классу Н₃. Вероятность того, что а течение года водитель класса H₁ попадёт хотя бы в одну аварию, равна 0,01, для водителя класса Н₂ эта вероятность равна 0,02, а для водителя класса Н₃ 0,08. Водитель А страхует свою машину и в течение года попадает в аварию. Какова вероятность того, что он относится к классу H₁?

7. В семье 5 детей. Найти вероятность того, что среди детей 2 мальчика, если вероятность рождения мальчика принимается 0,5.

6. В магазин вошли 5 покупателей. Найти вероятность того, что не менее трёх из них совершат покупки, если вероятность совершить покупку для каждого вошедшего одна и та же и равна 0,3.

7. В мастерской имеются 6 моторов. При существующем режиме работы вероятность того, что мотор в данный момент работает с полной нагрузкой, равна 0,8. Найти вероятность того, что с полной нагрузкой в данной момент работают не менее 5 моторов.

8. Вероятность наступления события А в каждом опыте равна 0,25. Найти наивероятнейшее число наступлений события А в 192 опытах и вероятность этого события.

9. Монету бросают 400 раз. Какова вероятность того, что герб при этом выпадет не менее 196, но не более 206 раз?

10. С вероятностью попадания при одном выстреле 0,7 охотник стреляет по дичи до первого попадания, но успевает сделать не более 5 выстрелов. Дискретная случайная величина х число промахов. Найдите 1). закон распределения х.

2). постройте многоугольник распределения.

11. .
13. ;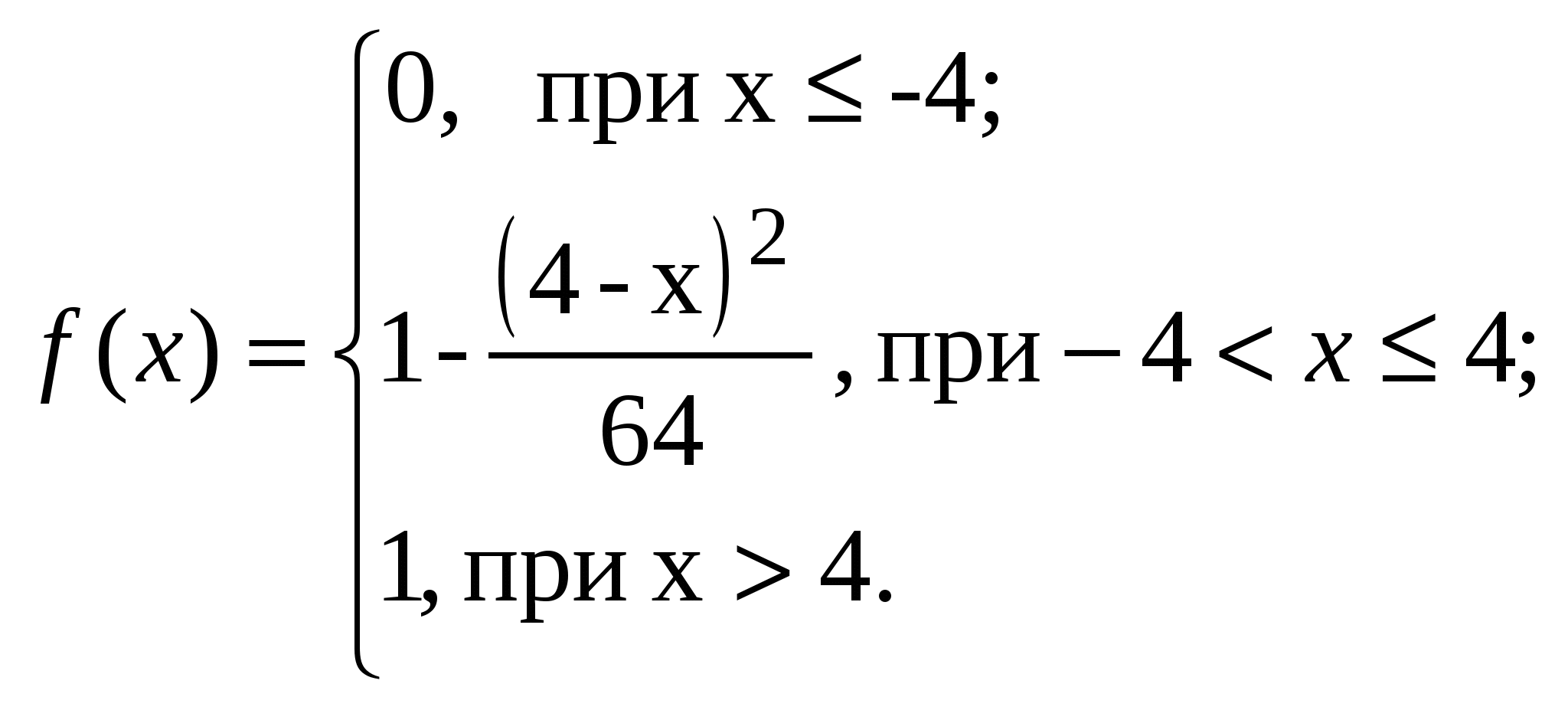
14. а=10, .

ВАРИАНТ 13

1. 
   В лотерее выпущено 20 билетов, 10 из которых выигрывают. Гражданин купил 5 билетов. Какова вероятность того, что по крайней мере один из купленных билетов выигрышный?
   
2. 
   В денежно – вещевой лотерее на 1000 билетов приходится 24 денежных и 10 вещевых выигрышей. Некто приобрел 2 билета. Какова вероятность выигрыша хотя бы одного билета?
   
3. 
   На сборку попадают детали с трёх автоматов. Известно, что первый автомат даёт 0,3 % брака, а второй 0,2 % и третий 0,4 %. Найти вероятность попадания на сборку бракованных деталей, если с первого автомата поступило 1000, со второго 2000, из третьего 2500 деталей.
   
4. 
   Имеются 2 урны. В первой 3 белых и 4 чёрных шара, во второй 2 белых и 3 чёрных. Из первой урны наудачу перекладывают во вторую 2 шара, а затем из второй урны извлекают 1 шар. Какой состав преложенных шаров наиболее вероятен, если шар, извлечённый из второй урны, окажется белым?
   
5. 
   Четыре стрелка независимо друг от друга стреляют по одной, делая каждый по одному выстрелу. Вероятности попадания для данных стрелков равны 0,4; 0,6; 0,7; 0,8. после стрельбы в мишени обнаружены 3 пробоины. Найти вероятность того, что промахнулся 4 стрелок.
   
6. 
   Рабочий обслуживает 5 одинаковых станков. Вероятность того, что в течении дня станок потребует регулировки, равна 1/3. Какова вероятность того, что в течении дня рабочему придётся регулировать 4 станка?
   
7. 
   Проведено 5 независимых испытаний, каждое из которых заключается в одновременном подбрасывании 2 монет. Найти вероятность того, что ровно в 3 испытаниях появилось по 2 герба.
   

8. Вероятность того, что покупателю требуется костюм 50-го размера, равна 0,2. Найти вероятность того, что среди 100 покупателей потребуют костюм 50-го размера 25 человек.

9.Вероятность появления успеха в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что число появления успеха будет заключено между 400 и 500.

10. Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка при одном выстреле равна 0,6, а для второго 0,7. Дискретная случайная величина х – число попаданий в мишень.

1) найдите закон распределения х;

2) постройте многоугольник распределения.

11.
13. ;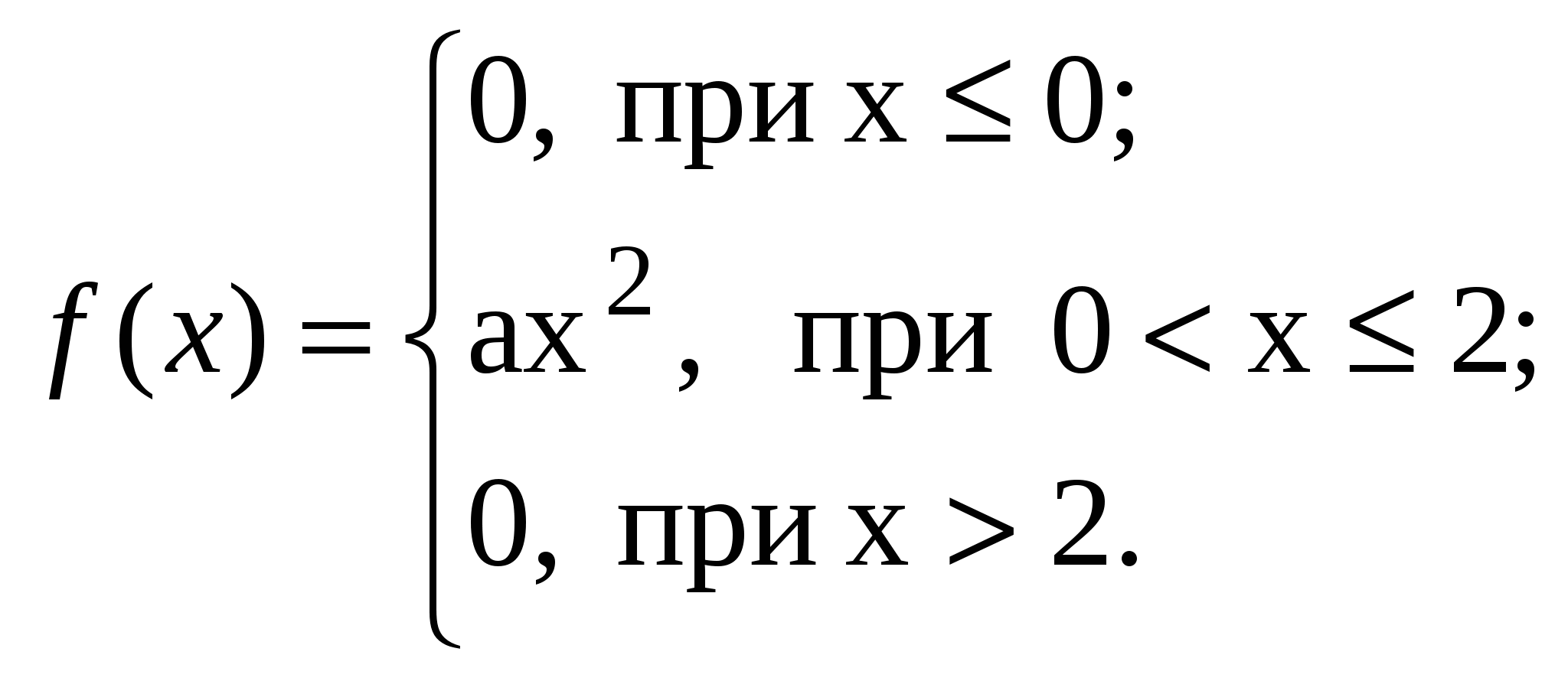
14. а = 10, .