семестровая работа (очная форма)). Теория вероятностей методические указания и варианты заданий типового расчёта
 Скачать 484.5 Kb. Скачать 484.5 Kb.
|
ВАРИАНТ 191. Среди группы из 10 человек 7 мужчин. Надо составить группы по 6 человек, в которые обязательно входят 4 мужчины. Найти вероятность появления такой группы. 2. Слово «карета», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробку. Из коробки наугад одну за другой. Какова вероятность получить при таком извлечении слово «ракета»? 3. Три стрелка производят по одному выстрелу. Вероятности попадания каждого в цель следующая: 0,9; 0,8; 0,7. Найти вероятность того, что в цель попадут только два стрелка. 4. Электролампы изготавливаются на 3-х заводах. Первый завод производит45 % общего количества электроламп, второй 40 %, третий 15 %. Продукция первого завода содержит 70 % стандартных ламп, второго 80 %, третьего 81 %. В магазине продукция всех трёх заводов. Какова вероятность того, что купленная в магазине лампа окажется стандартной? 5. Имеются 4 урны. В первой 1 белый и 1 черный шар, во второй 2 белых и 3 чёрных шара, в третьей 3 белых и 5 чёрных шаров, в четвёртой 4 белых и 7 чёрных шаров. Вероятности выбора каждой из урн следующие: 1/10, 1/5, 3/10, 2/5. Выбирают наугад одну из урн и вынимают из неё шар. Найти вероятность, что этот шар белый. 6. Из 10 деталей 4 окрашены. Вероятность того, что окрашенная деталь тяжелее нормы, равна 0,3, а для неокрашенной детали эта вероятность равна 0,1. Взятая наудачу деталь оказалась тяжелее нормы. Найти вероятность того, что она окрашена. 7. Трём студентам дано задание решить одинаковое количество задач. Вероятность сделать ошибку для первого студента равна 0,2, для второго 0,1, для третьего 0,15. Преподаватель наудачу извлекает одну тетрадь и находит ошибку. Найти вероятность того, что ошибся первый студент. 8. По самолёту производится четыре независимых выстрела. Вероятность попадания в самолёт при каждом выстреле равна 0,7. Чтобы вывести самолёт из строя, достаточно трёх попаданий. Найти вероятность того, что самолёт будет выведен из строя. 9. Монету бросали 4096 раз. При этом герб выпал 2068 раз. С какой вероятностью можно было ожидать этот результат? 10.На пути движения автомобиля 6 светофоров, каждый из них или разрешает или запрещает дальнейшее движение с вероятностью 0,5. Найдите закон распределения случайной величины х, равной числу светофоров, пройденных автомобилем до первой остановки. 11. 13. 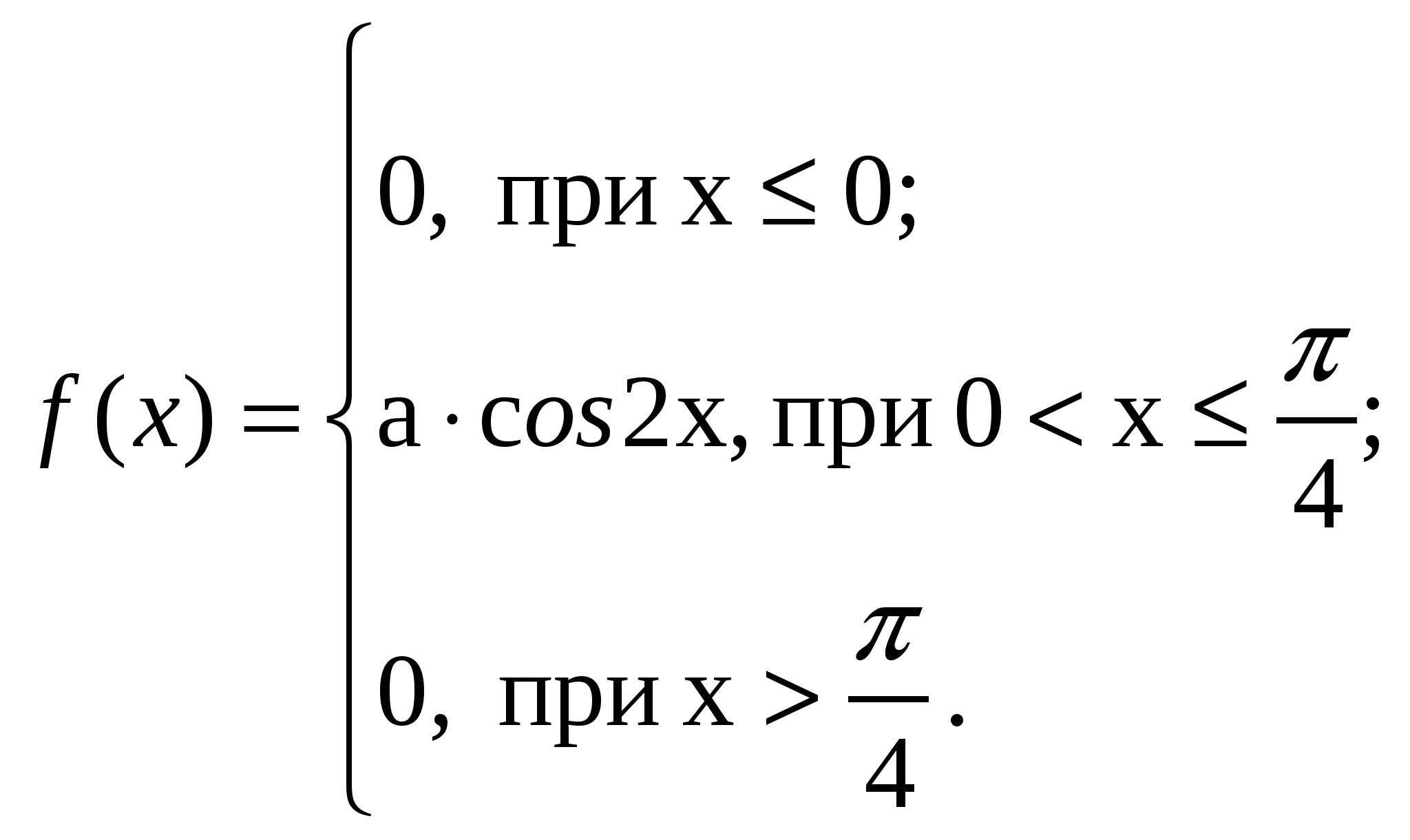 14. а = 5, ВАРИАНТ 201. Из полной колоды карт (52 карты) вынимают наугад сразу три карты. Найти вероятность того, что этими картами будут тройка, семерка, туз. 2. Вероятность попадания в цель только одним выстрелом из двух равна 0,32. Найти вероятность хотя бы одного попадания в цель при двух выстрелах. 3. В.двух ящиках находятся шары: в одном 2 белых и 5 чёрных, в другом 2 белых и 3 чёрных. Из первого во второй переложены три шара. Какова вероятность вынуть из второго ящика чёрный шар? 4. В ящик, содержащий 3 детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь. Первоначальный состав деталей в ящике неизвестен. 5. На склад поступает продукция трёх фабрик. Продукция первой фабрики составляет 20 %, второй 46 %, третьей 34 % от общего числа. Известно также, что средний процент нестандартных изделий для первой фабрики равен 3 %, для второй 2 %, для третьей 1 %. Найти вероятность того, что наудачу взятое изделие произведено на первой фабрике, если оно оказалось стандартным. 6. В кондитерском цехе выпускаются торты и пирожные, причём пирожных в 4 раза больше. 10 % тортов и 35 % пирожных изготавливают с орехами. Наугад выбранное изделие оказалось с орехами. Какова вероятность того, что это торт? 7. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 30 телевизоров хотя бы один не потребует ремонта. 8. Вероятность изготовления детали высшего сорта на данном станке равна 0,4. Найти наивероятнейшее число деталей высшего сорта среди 24 деталей и вероятность этого события. 9. На склад поступает продукция трёх фабрик, причём изделия первой фабрики на складе составляют 30 %, второй 32 %, третьей 38 %. В продукции первой фабрики 60 % изделий высшего сорта, второй 20%, третьей 50 %. Найти вероятность того, что среди 1100 наудачу взятых со склада изделий высшего сорта заключено между 330 и 550. 10. Вероятность изготовления нестандартной детали 0,1. Из партии контролёр берет деталь и проверяет её на стандартность. Если деталь оказывается нестандартной, то дальнейшие испытания прекращаются, а вся партия задерживается. Если же деталь оказывается стандартной, то контролёр берёт следующую и т.д., но всего он проверяет не более 6 деталей. Найдите закон распределения случайной величины х, равной числу проверяемых деталей. 11. 13. 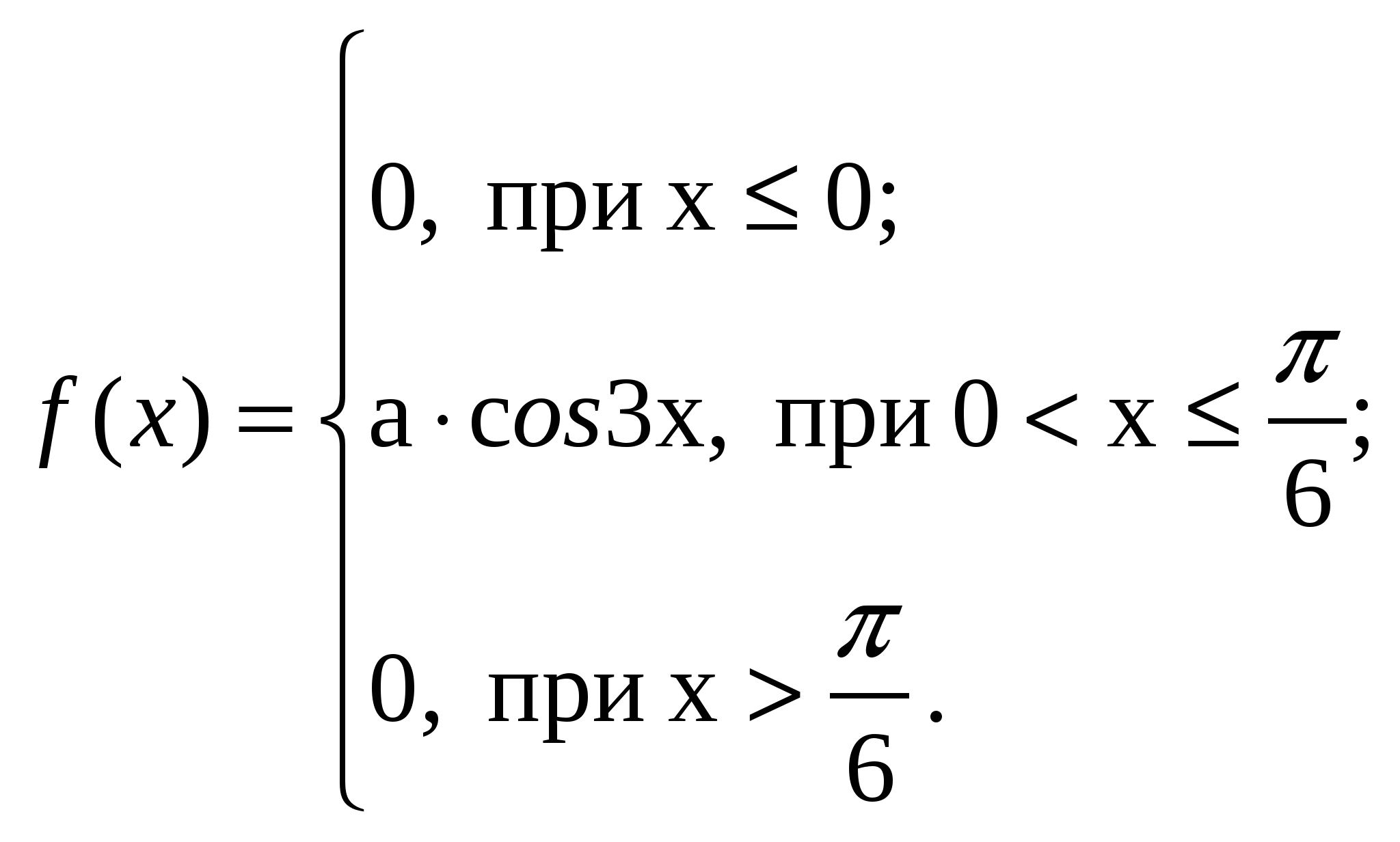 14. а = 5, ВАРИАНТ 21 1. Среди дружинников 3 девушки и 7 юношей. Требуется путём жеребьёвки избрать на дежурство 3 дружинников. Чему равна вероятность того, что при извлечении одного за другим трёх «жребиев» окажутся избранными три юноши? 2. На пяти одинаковых карточках написаны буквы: К, Н, И, Г, А. Выкладываем наудачу эти карточки подряд. Какова вероятность того, что при этом получится слово «книга»? 3. На фабрике работают три станка. При этом производительность первого вдвое выше производительности второго и в 1,5 раза выше производительности третьего. На первом из каждых десяти изделий три изделия первого сорта. Во втором 5 изделий, на третьем 4 изделий. Найти вероятность того, что наугад взятое со склада изделие будет первого сорта. 4. В двух ящиках находятся шары: в одном 3 белых и 2 чёрных, в другом 4 белых и 5 чёрных. Из каждого ящика вынули по одному шару, а затем оставшиеся шары ссыпали в один ящик. Какова вероятность вынуть из него белый шар? 5. Телефонное сообщение состоит из сигналов «точка» и «тире». В среднем искажается 2/5 сообщений «точка» и 1/3 «тире». Известно, что среди передаваемых сигналов «точка» и «тире» встречаются в отношении 5:3. Определить вероятность того, что принят передаваемый сигнал, если принят сигнал «тире». 6. В часовую мастерскую поступают в среднем 40 % часов с дефектом А, 25 % с дефектом В и 35 % с дефектом С. Вероятность ремонта часов с дефектом А равна 0,6, с дефектом В0,5 с дефектом С 0,8. Часы, поступившие в ремонт, полностью отремонтировали. Найти вероятность того, что у часов был дефект С. 7. База заказала на некоторый день 4 автомашины, имея 6 потребителей, каждый из которых даёт по одному заказу в день независимо друг от друга с вероятностью 0,4. Определить вероятность того, что машин не хватит для удовлетворения всех заказов? 8. Предположим, что вероятность выздоровления больного в результате применения нового способа лечения равна 0,8. Сколько вылечивается из 100 больных с вероятностью 0,75? 9. Найти вероятность того, что в партии из 900 изделий число изделий высшего сорта заключено от 600 до 700. Найти наивероятнейшее число изделий высшего сорта в партии, если вероятность его появления равна 0,8. 10.Два стрелка стреляют по одной мишени, делая независимо друг от друга по два выстрела. Вероятность попадания в мишень для первого стрелка равна 0,4, для второго 0,6. Найдите закон распределения случайной величины х, равной общему числу попаданий в мишень. 11. 13. 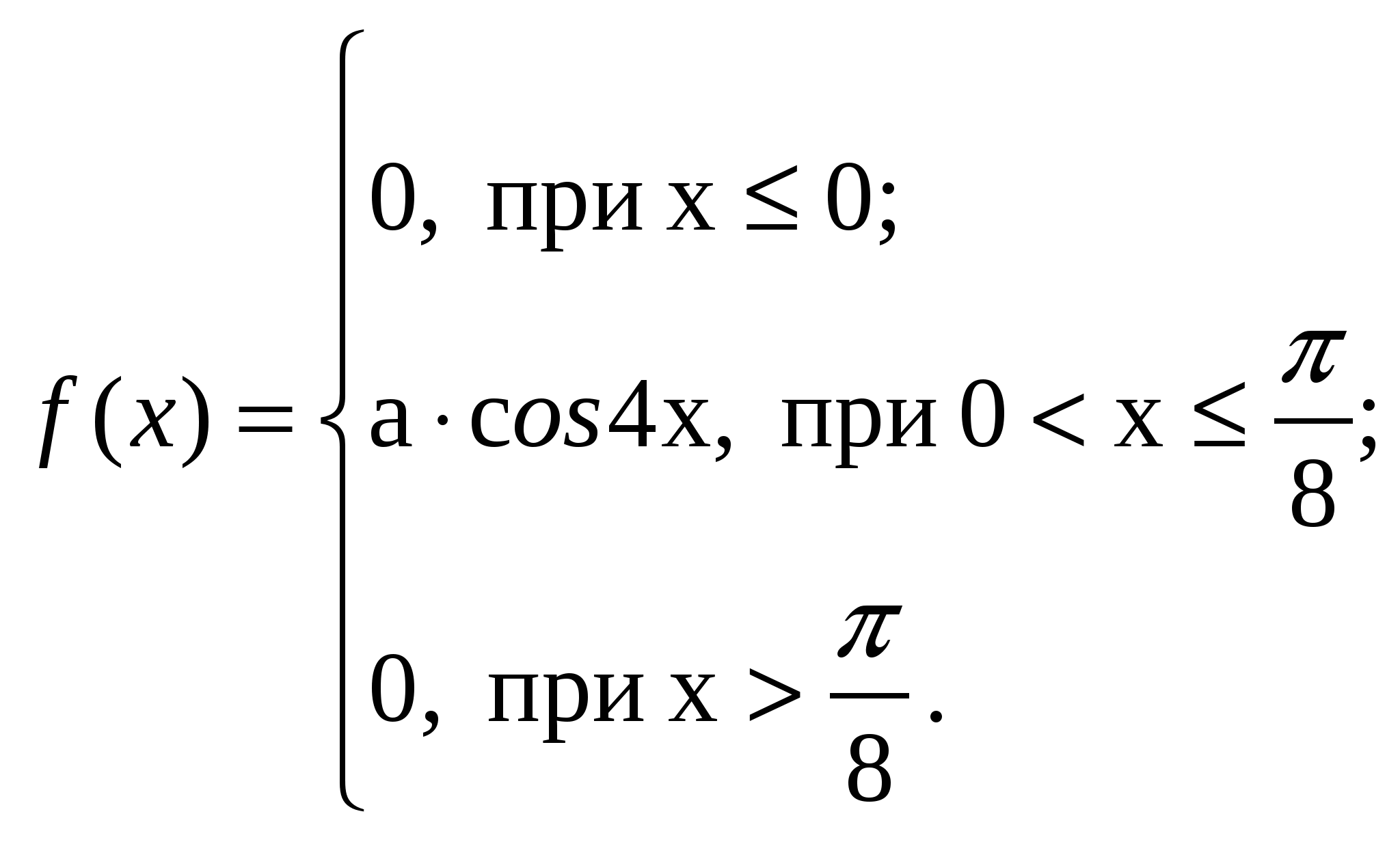 14. а = 7, |
