семестровая работа (очная форма)). Теория вероятностей методические указания и варианты заданий типового расчёта

• Название: Теория вероятностей методические указания и варианты заданий типового расчёта
• Анкор: семестровая работа (очная форма)).doc
• Дата: 02.04.2018
• Размер: 484.5 Kb.
• Имя файла: семестровая работа (очная форма)).doc
• Тип: Методические указания; #17519
• страница: 12 из 13

ВАРИАНТ 26

1. В урне 6 белых, 4 чёрных, 5 красных шаров. Из урны наугад вынимают 5 шаров. Найти вероятность того, что среди них окажутся 2 белых и 1 чёрный шар.

2. Из множества 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 наудачу выбрано число q, после чего составлено уравнение +4x+q=0. Какова вероятность того, что корни этого уравнения окажутся целыми рациональными числами?

3. Швейные заготовки поступают из двух цехов; 70 % из первого и 30 % из второго. Заготовки первого цеха содержат 10 % брака, второго 20 %. Найти вероятность того, что наугад взятая заготовка без дефектов.

4. Имеются две урны. В первой находятся 1 белый шар, 3 чёрных и 4 красных, во втором 3 белых, 2 чёрных и 3 красных. Из каждой урны наугад извлекают по одному шару, после чего сравнивают их цвета. Найти вероятность того, что цвета вытащенных шаров не совпадают.

5. Из 18 стрелков 5 попадают в мишень с вероятностью 0,8; 7 с вероятностью 0,7; 4 с вероятностью 0,6 и 2 с вероятностью 0,5. Наудачу выбранный стрелок не попал в мишень. К какой группе вероятнее всего он принадлежит?

6. В группе из 20 мужчин и 300 женщин 5 % мужчин и 3 % женщин страдают бронхитом. Наугад выбранное для обследования лицо страдает бронхитом. Какова вероятность того, что это женщина?

7. Вероятность обнаружения бракованного изделия в отдельном испытании равна 0,25. Какова вероятность того, что при трёхкратном испытании стандартное изделие появится не менее двух раз?

8. Вероятность события в каждом из 100 испытаний равна 0,8. Найти вероятность того, что это событие не появится в этих испытаниях равно 10 раз.

9. Пусть вероятность того, что покупателю овощного магазина потребуется картошка, равна 0,2. Найти вероятность того, что из 625 покупателей более 120 потребуют картошку.

10. Устройство состоит из 3 элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.

11.
13. ;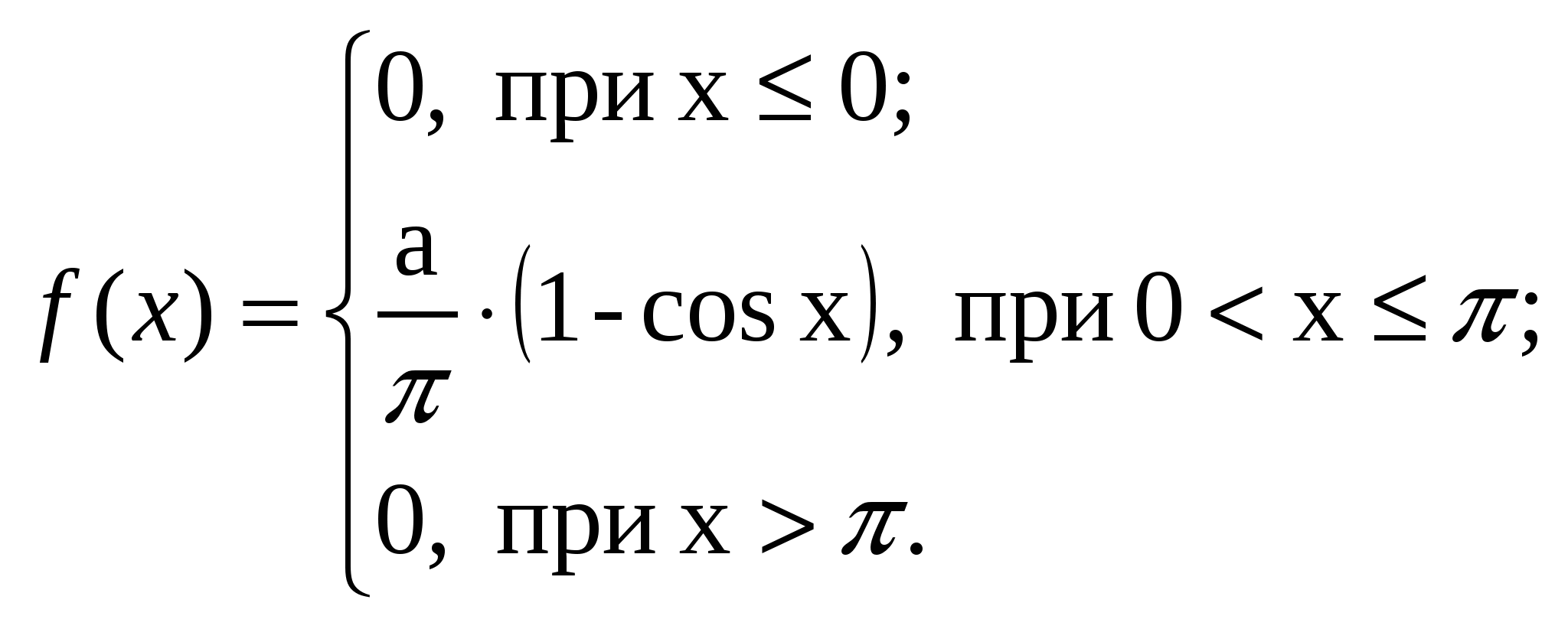
14. а = 12,
ВАРИАНТ 27
1. Из партии, состоящей из 20 пар ботинок, для проверки отбирают 4 пары. Партия содержит 3 бракованных пары. Какова вероятность того, что в число отобранных войдёт не более одной бракованной пары ботинок?

2. Изделия высшего качества в партии составляет 80 %. Какова вероятность того, что из двух наугад взятых изделий хотя бы одно не будет изделием высшего качества?

3. В урнах находятся шары, отличающиеся только цветом, причем в первой урне 5 белых шаров, 11 чёрных и 8 красных, а во второй соответственно 10, 8 и 6.Из обеих урн наудачу извлекаются по одному шару. Какова вероятность того, что оба шара одного цвета?

4. На фабрике работают 3 станка. При этом производительность второго станка вдвое выше производительности первого и в 1,5 раза выше производительности третьего. На 1-ом станке из каждых 10 изделий 5 изделий высшего сорта. на втором 6 изделий и на третьем 7 изделий. Найти вероятность того, что взятое наугад со склада изделие имеет первый сорт.

5. 
   Вероятность промаха при каждом выстреле для 3 стрелков равны соответственно 0,1, 0,2 и 0,3. Какова вероятность того, что будет попадание в цель, если первый стрелок делает выстрелы в 30 % случаев, второй в 50 % и третий в 20 %?
   
6. 
   Турист может пообедать в трёх столовых города. Вероятность того, что он отправится к первой столовой 1/3, ко второй 1/2, а к третьей 1/6.Вероятность того, что эти столовые закрыты следующие: первая 1/6, вторая 1/5 и третья 1/8.Турист пришёл в одну из столовых и пообедал. Какова вероятность того, что он направился ко второй столовой?
   
7. 
   Игральная кость бросается 5 раз. Найти вероятность того, что 3 раза появится число очков, кратное двум.
   
8. 
   Вероятность того, что хоккеист реализует буллит, равна 0,7.Произведён 21 бросок. Найти вероятнейшее число попаданий и вероятность этого события.
   
9. 
   Вероятность выигрыша в лотерею равна 0,1. Какова вероятность того, что из 400 билетов, купленных организацией, будет более 20 проигрышных?
   
10. 
    В партии 10 % нестандартных деталей. Наудачу отобраны 4 детали. Написать закон распределения дискретной случайной величины х – числа нестандартных деталей среди 4 отобранных и построить многоугольник полученного распределения.
    

11.
13.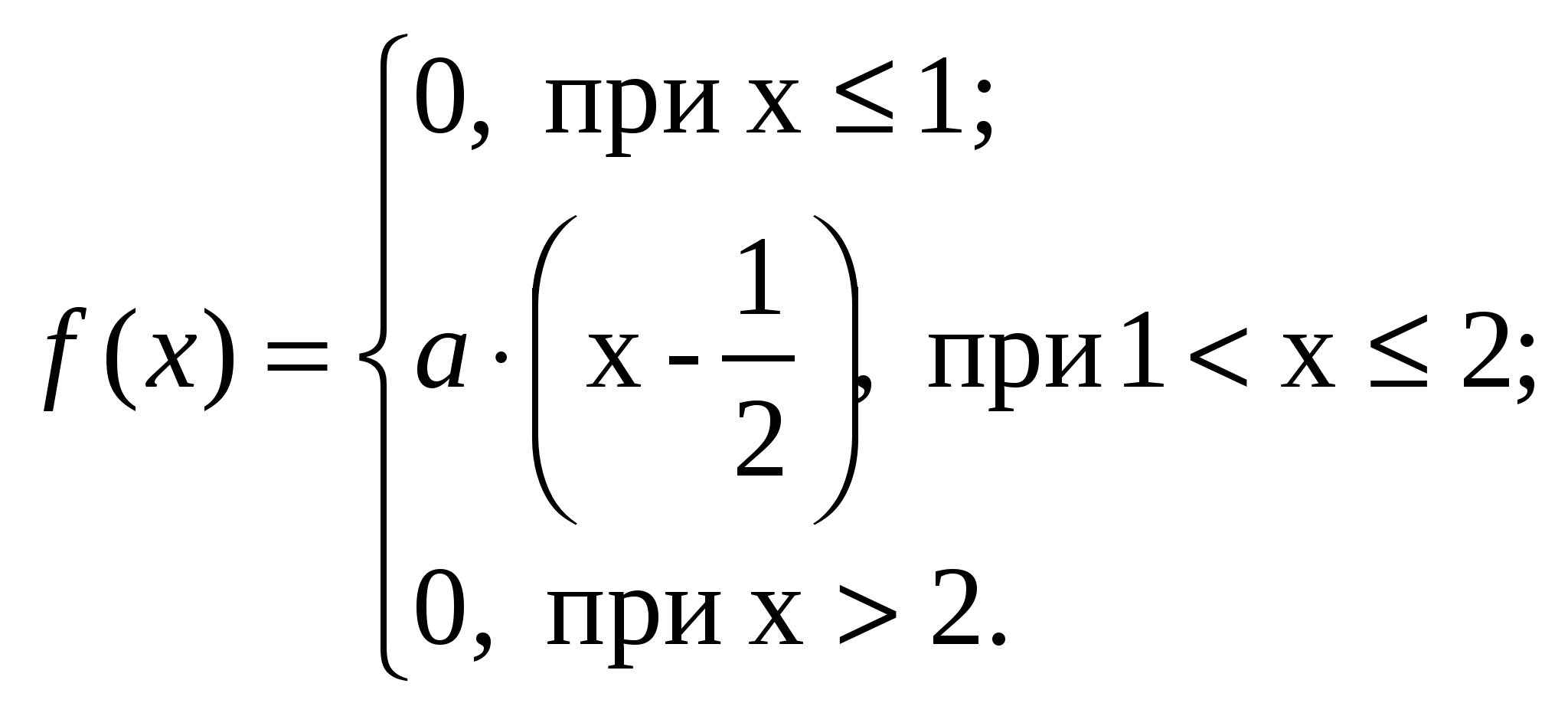
14. а = 14,