семестровая работа (очная форма)). Теория вероятностей методические указания и варианты заданий типового расчёта

• Название: Теория вероятностей методические указания и варианты заданий типового расчёта
• Анкор: семестровая работа (очная форма)).doc
• Дата: 02.04.2018
• Размер: 484.5 Kb.
• Имя файла: семестровая работа (очная форма)).doc
• Тип: Методические указания; #17519
• страница: 1 из 13

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

(ФИЛИАЛ) ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ

ТЕОРИЯ ВЕРОЯТНОСТЕЙ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ВАРИАНТЫ ЗАДАНИЙ ТИПОВОГО РАСЧЁТА


ЧАСТЬ П .

РПК «Политехник»

Волгоград

2004.

ЦДК…

Теория вероятностей. Методические указания и варианты заданий типового расчёта. Составитель: С. В. Мягкова, У. А. Бурцева, А. А. Кулеша: Волгоград. гос. техн. ун., Волгоград, 2004.

Настоящая работа адресована студентам всех специальностей изучающих курс теории вероятностей.

Работа содержит программу курса и условия заданий типового расчёта.
Табл.___ Рис. ____ Библиогр.:_____назв.____

Рецензент В. Ф. Казак.


Печатается по решению редакционно-издательского совета Волгоградского государственного технического университета.

© Волгоградский

государственный

технический

университет, 2004.

§ 1. Программа курса

1. 
   Случайные события. Понятие случайного события. Вероятность события. Классическое и статистическое определение вероятности. Теорема сложения вероятностей. Условные вероятности. Независимые события. Теорема умножения вероятностей. Формула полной вероятности. Формула Байеса. Биномиальное распределение. Формула Пуассона и Лапласа.
   
2. 
   Случайные величины. Дискретные и непрерывные случайные величины. Функция распределения и плотность распределения случайной величины. Математическое ожидание и дисперсия, их свойства. Основные законы распределения. Закон больших чисел. Неравенство и теорема Чебышева. Теорема Бернулли. Понятие о центральной предельной теореме.
   

§ 2 Задачи типового расчета
Уважаемые студенты! В типовом расчёте каждый вариант составлен отдельно. В задачах с № 1 по № 10 вопрос указан в тексте задачи.

В задаче № 11 найти:

1. математическое ожидание М(х)

2. дисперсию D(x) - двумя способами

3. среднее квадратическое отклонение σ(х)

4. составить функцию распределения величины Х и постройте её график.

В задаче № 12:

1. 
   составьте закон распределения величины У=50-2Х, величина Х задана законом своего распределения в задаче № 11.
   
2. 
   вычислите математическое ожидание и дисперсию составленной величины дважды, пользуясь свойствами математического ожидания, дисперсии и непосредственно составленным законом распределения величины У = 5 0- 2х.
   

В задаче № 13:

а) варианты № 1 - 12: случайная величина х задана функцией распределения F(х). Требуется убедиться, что заданная функция F(x) является функцией распределения некоторой непрерывной случайной величины. В случае положительного ответа найдите:

1. дифференциальную функцию

2. математическое ожидание величины х

3. дисперсию величины х

4. среднее квадратическое отклонение

5. постройте графики дифференциальной и интегральной функций

6. Определите вероятность попадания величины х в (а.; в)

б) Варианты № 13 - 30: случайная величина х задана дифференциальной функцией f(x). Найдите;

1. параметр а

2. математическое ожидание М(х)

3. дисперсию D(x)

4. среднее квадратнческое отклонение σ(x)

5. постройте график f(х)

6. вычислите вероятность попадания величины х в (;)

7. найдите функцию распределения F(x) и постройте её график.

В задаче № 14:

заданы математическое ожидание а и среднее квадратическое отклонение σ нормально распределённой случайной величины х. Найти вероятность того, что случайная величина х попадёт в (;).

Все задания рекомендуется сначала переписать в отдельную тетрадь, а затем необходимо преступить к их выполнению в любом порядке, подробно давая пояснения и приводя формулы. Каждый типовой расчет сначала выполняется письменно, затем в форме устной беседы с преподавателем защищается.
§ 3. Типовой расчёт
ВАРИАНТ 1

1. Среди 25 студентов, где 10 девушек, разыгрываются 5 билетов. Определить вероятность того, что среди обладателей билетов окажутся две девушки.

2. Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что в течение часа не потребует внимания 1-й станок, равна 0,9, 2-ой 0,8, 3-й 0,85. Найти вероятность того, что в течение часа один станок не потребует внимания рабочего.

3. На трёх автоматических станках изготавливаются одинаковые детали. Известно, что 30 % продукции производится первым станком, 25 % вторым и 45 % третьим. Вероятность изготовления детали, отвечающей стандарту, на первом станке равна 0,99, на втором 0,988 и на третьем 0,98. Изготовленные в течение дня на трёх станках не рассортированные детали находятся на складе. Определить вероятность того, что взятая наугад деталь соответствует стандарту.

4. Имеются две урны. В первой урне два белых и три чёрных шара, во второй - три белых и пять чёрных. Из первой и второй урны, не глядя, берут по одному шару и кладут их в третью урну. Шары в третьей урне перемешивают и берут из неё наугад один шар. Найти вероятность того, что этот шар белый.

5. Турист, заблудившись в лесу, вышел на поляну, от которой в разные стороны идут пять дорог. Если турист пойдёт, по первой дороге, то вероятность выхода туриста из леса в течение часа составляет 0,6; если по второй 0,3; если по третьей 0,2; по четвёртой 0,1; по пятой 0,1. Какова вероятность того, что турист вышел из леса?

6. Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится четыре независимых выстрела. Найти вероятность того, что будет одно попадание в мишень.

7. Рабочий обслуживает пять однотипных станков. Вероятность того, что станок потребует внимания рабочего в течение дня равно 0,3. Найти вероятность того, что в течение дня этих требований будет от трёх до пяти.

8. При установившемся технологическом процессе 80 % всей произведённой продукции высшего сорта. Найти наивероятнейшее число изделий высшего сорта в партии из 225 изделий и вероятность этого события.

9. Вероятность получения по лотерее выигрышного билета равна 0.1. Какова вероятность того, что среди 400 наугад купленных билетов не менее 40 и не более 50 выигрышей?

10. Из 25 контрольных работ, среди которых 5 оценены на "отлично", наугад извлекаются 4 работы. Найти закон распределения дискретной величины х, равной числу оцененных на "отлично" работ среди извлечённых. Чему равна вероятность события х > 0?

11. .
13.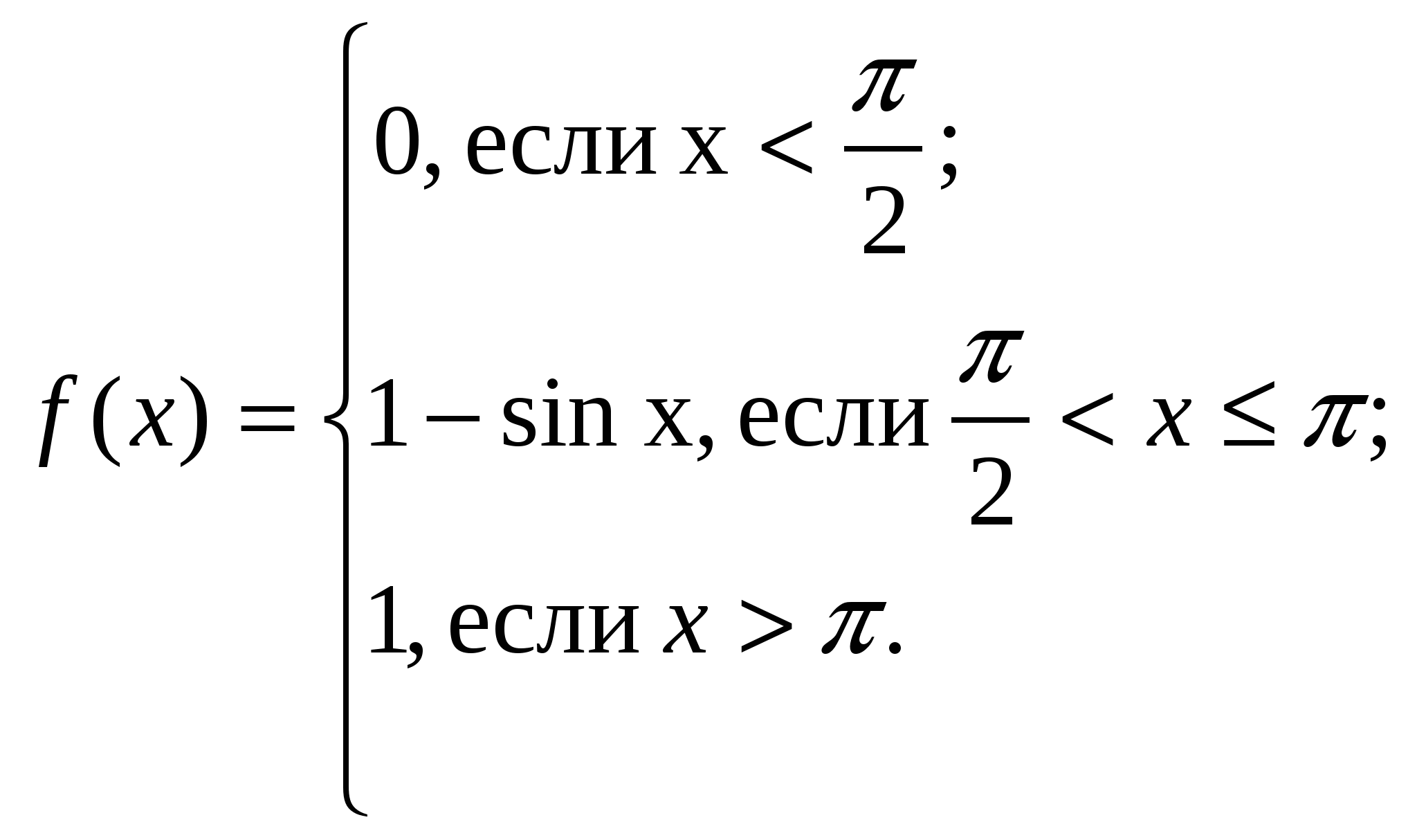

;

14. a = 15, /