семестровая работа (очная форма)). Теория вероятностей методические указания и варианты заданий типового расчёта
 Скачать 484.5 Kb. Скачать 484.5 Kb.
|
ВАРИАНТ 51. В мастерскую для ремонта поступило 15 телевизоров. Известно, что шесть из них нуждаются в общей регулировке. Мастер берёт первые пять попавшихся телевизоров. Какова вероятность того, что два из них нуждаются в общей регулировке. 2. Три орудия ведут огонь по цели, вероятность попадания в которую при одном выстреле из первого орудия 0,5, из второго 0,6, из третьего 0,7. Зная, что каждое орудие стреляет один раз. Найти вероятность поражения цели, если для этого достаточно двух попаданий. 3. Из пяти букв разрезной азбуки составлено слово «КНИГА». Неграмотный мальчик перемешал буква, а потом наугад их собрал. Какова вероятность того, что он опять составит слово «КНИГА» 4. С первого автомата на сборку поступило 40 %, со второго 35 %, с третьего 25 %. Среди деталей первого автомата 0,2 % бракованных, второго 0,3 %, третьего 0,5 %. Найти вероятность того, что поступившая на сборку деталь бракованная. 5. Имеются два одинаковых ящика с шарами. В первом ящике 2 белых и 1 чёрный, во втором 1 белый и 4 чёрных шара. Наугад выбирают один ящик и вынимают из него шар. Какова вероятность того, что вынутый шар окажется белым? 6. Один из трех стрелков вызывается на линию огня и проводит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго 0,5, для третьего 0,8, Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком. 7. Стрелок стреляет по цели до первого попадания. Найти вероятность того, что у стрелка останется хотя бы один неизрасходованный патрон, если он получил 5 патронов и вероятность попадания в цель при каждом выстреле постоянна и равна 0,2. 8. Вероятность встретить на улице знакомого равна 0,2 Сколько среди первых 100 случайных прохожих можно надеяться встретить знакомых с вероятностью 0,957? 9. Всхожесть семян данного растения равна 0,9. Найти вероятность того, что из 900 посаженных число проросших будет заключено между 790 и 890. 10. В коробке имеются 7 карандашей, из которых 4 красные. Из этой коробки наудачу извлекаются 3 карандаша. 1). Найдите закон распределения случайной величины х, равной числу красных карандашей в выборке. 2). Постройте многоугольник распределения. 11. 13. 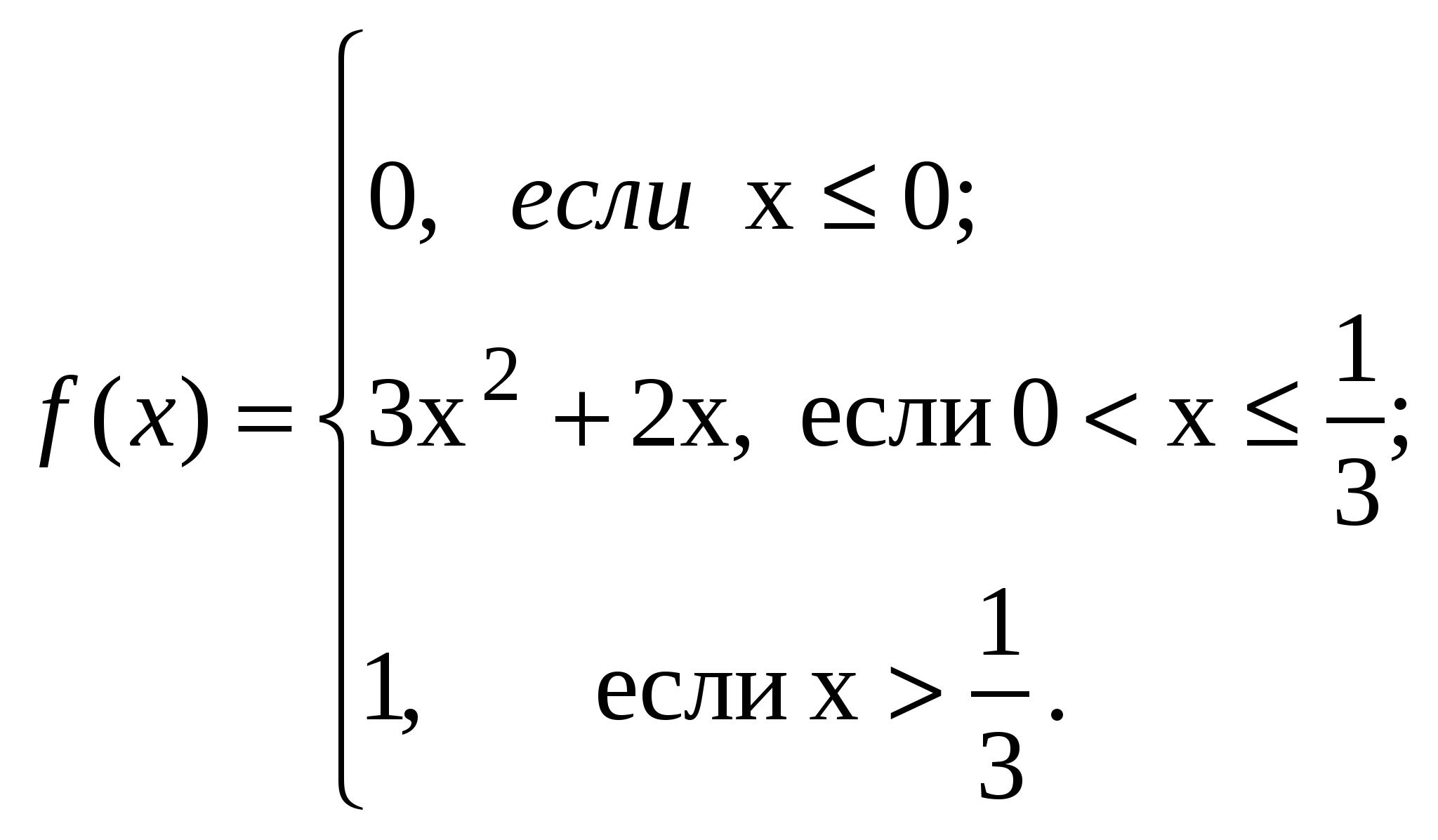 14. ВАРИАНТ 6 1. В бригаде 4-е женщины и 3-е мужчин. Среди бригады разыгрывается 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется две женщины и двое мужчин? 2. В одном ящике 6 белых и 4 чёрных шарика. Во втором 7 белых и 3 черных. Из каждого ящика наугад вынимают по одному шарику. Чему равна вероятность того, что оба шарика окажутся белыми? 3. Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения нестандартной детали на первом автомате равна 0,075, на втором 0,09. Производительность второго автомата вдвое больше, чем первого. Найти вероятность того, что наугад взятая с конвейера деталь нестандартная. 4. Имеются две партии одинаковых изделий по 15 и 20 штук, причём в первой партии два, во второй три бракованных изделия. Наугад взятое изделие из первой партии переложено во вторую, после чего выбирается наугад одно изделие из второй партии. Определить вероятность того, что выбранное изделие является бракованным. 5. В специализированной больнице в среднем 50 % больных с заболеванием К, 30 % с заболеванием Н, 20 % с заболеванием М. Вероятность полного лечения болезни К равна 0,7, дня болезней Н и М эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием? 6. Для прядения смешаны поровну белый и окрашенный хлопок. Найти вероятность среди 5 случайно выбранных волокон смеси обнаружить менее двух окрашенных. 7. 30 % изделий данного предприятия это продукция высшего сорта. Некто приобрёл 6 изделий, изготовленных на этом предприятии. Чему равна вероятность, что 4 из них высшего сорта? 8. Предположим, что вероятность выздоровления больного в результате применения нового способа лечения равна 0,8. Сколько вылечившихся из 100 больных можно ожидать с вероятностью 0,75? 9. Какова вероятность того, что в столбике из 100 наугад отобранных монет число монет, расположенных «гербом» вверх, будет от 45 до 55? 10. Из 25 контрольных работ, среди которых 5 оценены на "отлично", наугад извлекаются 3 работы. Найти закон распределения дискретной случайности величины х, равной числу оцененных на "отлично" работ среди извлеченных .Чему равна вероятность события х > 0 ? 11. 13 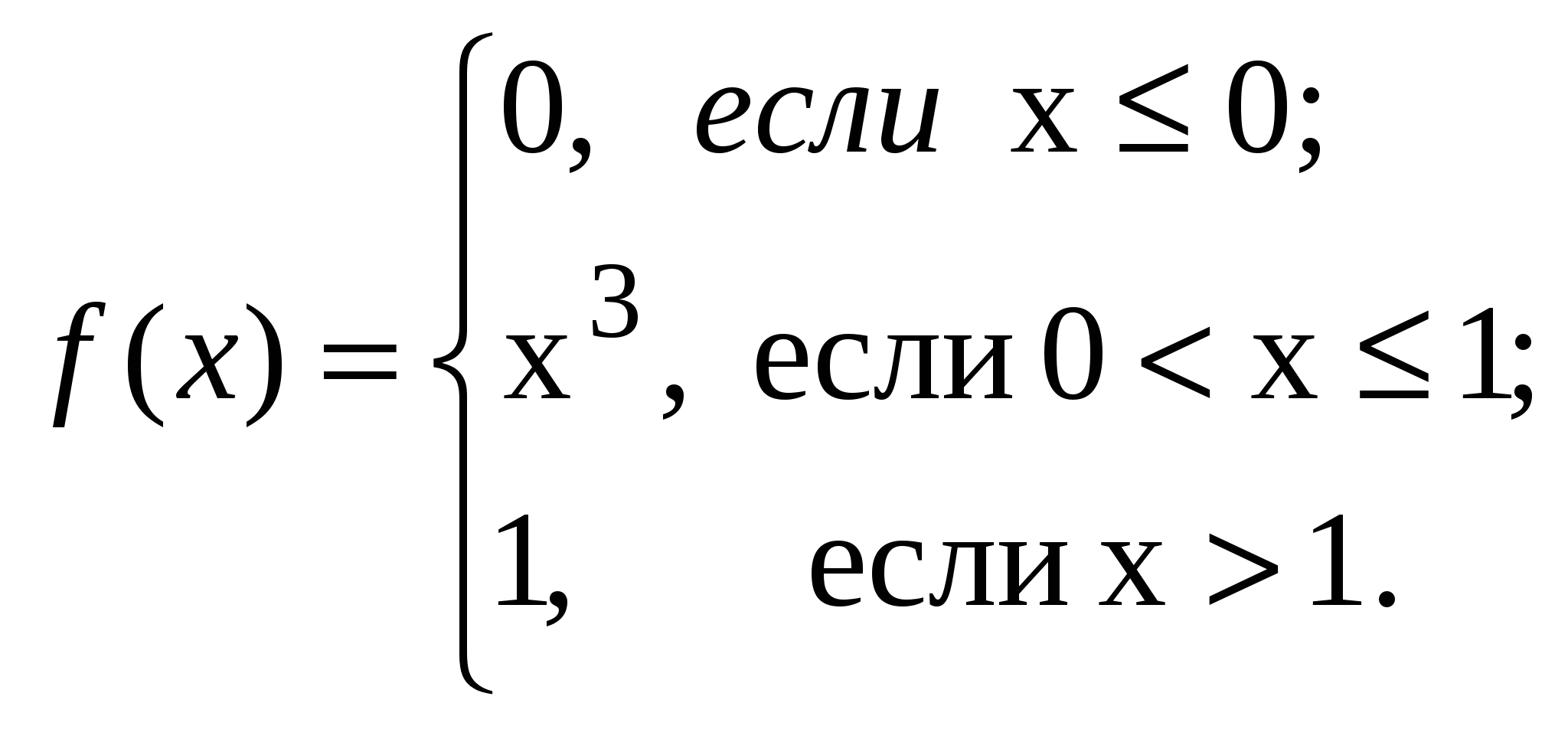 14. ВАРИАНТ 7 1. В урне 4 белых и 4 чёрных шара Из этой урны наудачу извлекли 5 шаров. Какова вероятность того, что 2 из них белые, а 3 чёрные? 2. Три стрелка ведут стрельбу по одной и той же мишени. Вероятность попадания в мишень дня первого стрелка равна 0,2, дня второго 0,3, для третьего 0,4. Найти вероятность того, что мишень поражена дважды. 3 В цехе работает 20 станков. Из них 10 марки А, 6 марки В н 4 марки С. Вероятность того, что качество детали окажется отличным для этих станков соответственно равна 0,9, 0,8, 0,7. Какой процент отличных деталей выпускает цех в целом? 4. Среди шести винтовок пристреленными оказываются только две. Вероятность попадания из пристреленной винтовки равна 0,9, а из непристреленной 0,7. Выстрелом одной наугад взятой винтовки цель поражена. Определить вероятность того, что взята пристреленная винтовка. 5. На склад поступает продукция трёх фабрик. Причем продукция первой фабрики составляет 20 %, второй 46 %, третьей 34 %. Известно также, что средний процент нестандартных изделий для первой фабрики равен 3 %, для второй 2 % и, наконец, для третьей 1 %. Найти вероятность того, что наугад взятое изделие произведено на первой фабрике, если оно оказалось нестандартным. 6. Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того. что из пяти посеянных семян взойдут не менее трёх? 7. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,8 и не зависит от номера выстрела. Найти наиболее вероятное число попаданий в мишень при 5 выстрелах и соответствующую этому числу вероятность. 8. Вероятность рождения мальчика примем равной 0,5. Найти вероятность того, что среди 400 новорождённых детей будет 200 мальчиков. 9. Вероятность появления события А в каждом из 15000 независимых испытаний равна 0,4. Найти вероятность того, что число появлений события заключено между 5700 и 6300. 10. Имеются 5 ключей, из которых только один подходит к замку. Найдите закон распределения случайной величины х, равной числу проб при открывании замка, если испробованный ключ в последующих опробованиях не участвует. 13. 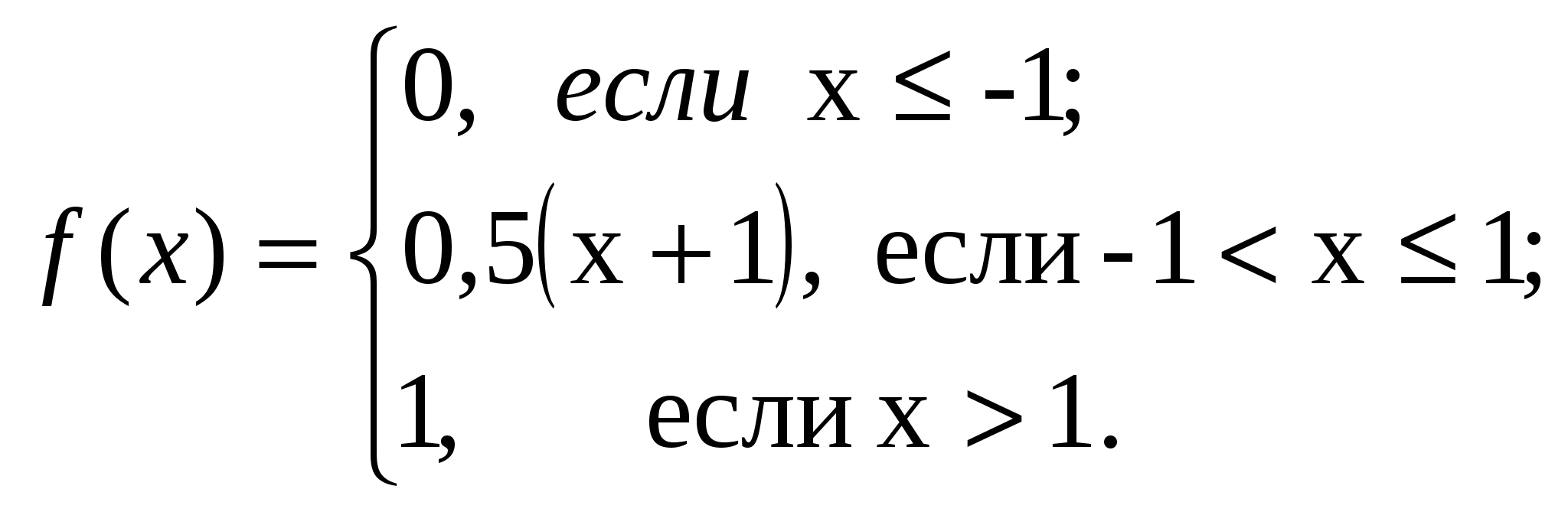 14.. |
