семестровая работа (очная форма)). Теория вероятностей методические указания и варианты заданий типового расчёта
 Скачать 484.5 Kb. Скачать 484.5 Kb.
|
ВАРИАНТ 21. В урне 4 белых и 5 чёрных шаров. Из урны наугад вынимают два шара. Найти вероятность того, что один из шаров белый, а другой чёрный. 2 На девяти карточках написаны буквы: А, А, А. М, М, Т, Т, Е, И, К. После тщательного перемешивания вынимают наугад одну карточку за другой и раскладывают их в том порядке, в каком они были вынуты. Найти вероятность того, что на карточках будет написано слово «МАТЕМАТИКА». 3. В группе из 20 стрелков имеются 4 отличных, 10 хороших и 6 посредственных стрелков. Вероятность попадания в цель при одном выстреле для отличника равна 0,9, для хорошего 0,7, для посредственного 0,5. На линию огня вызывают двух стрелков. Они производят по одному выстрелу. Найти вероятность того, что стрелки попадут в цель. 4. На распределительной базе находятся электрические лампочки, изготовленные на двух заводах. Среди них 60 % изготовлено на первом заводе и 40 % на втором. Известно, что из каждых ста лампочек, изготовленных на первом заводе, 90 соответствуют стандарту, а из 100 лампочек, изготовленных на втором заводе, соответствуют стандарту 80. Определить вероятность того, что взятая наугад лампочка с базы будет соответствовать стандарту. 5. Счётчик регистрирует частицы трех типов А, В и С. Вероятность попадания этих частиц Р(А) = 0,2, Р(В) = 0,5, Р(С) = 0,3. Частицы каждого из этих типов счётчик улавливает с вероятностью Р1 = 0,8, Р2 = 0,2, Р3 = 0,4. Счетчик отметил частицу. Определить вероятность того, что это была частица типа В. 6. По данным технического контроля, в среднем 2 % изготовляемых на заводе автоматических станков нуждаются в дополнительной регулировке. Чему равна вероятность того, что из четырёх изготовленных станков два нуждаются в дополнительной регулировке. 7. Событие В наступает только в том случае, если событие А появляется не менее 3 - х раз. Определить вероятность события В, если вероятность события А при одном опыте равна 0,4 и проведено 5 независимых опытов. 8. Вероятность изготовления изделия отличного качества равна 0.9. Изготовлено 100 изделий. Чему равно наивероятнейшее число изделий отличного качества и вероятность такого числа изделий отличного качества? 9. Игральную кость бросаем 18000 раз. Какова вероятность того, что шестёрка появится не менее 2000 и не более 3000 раз? 10. Дискретная случайная величина х – число мальчиков в семьях с 5 детьми. Предполагая равновероятным рождения мальчика и девочки: а) найдите закон распределения х; б) постройте многоугольник распределения. 11. 13. 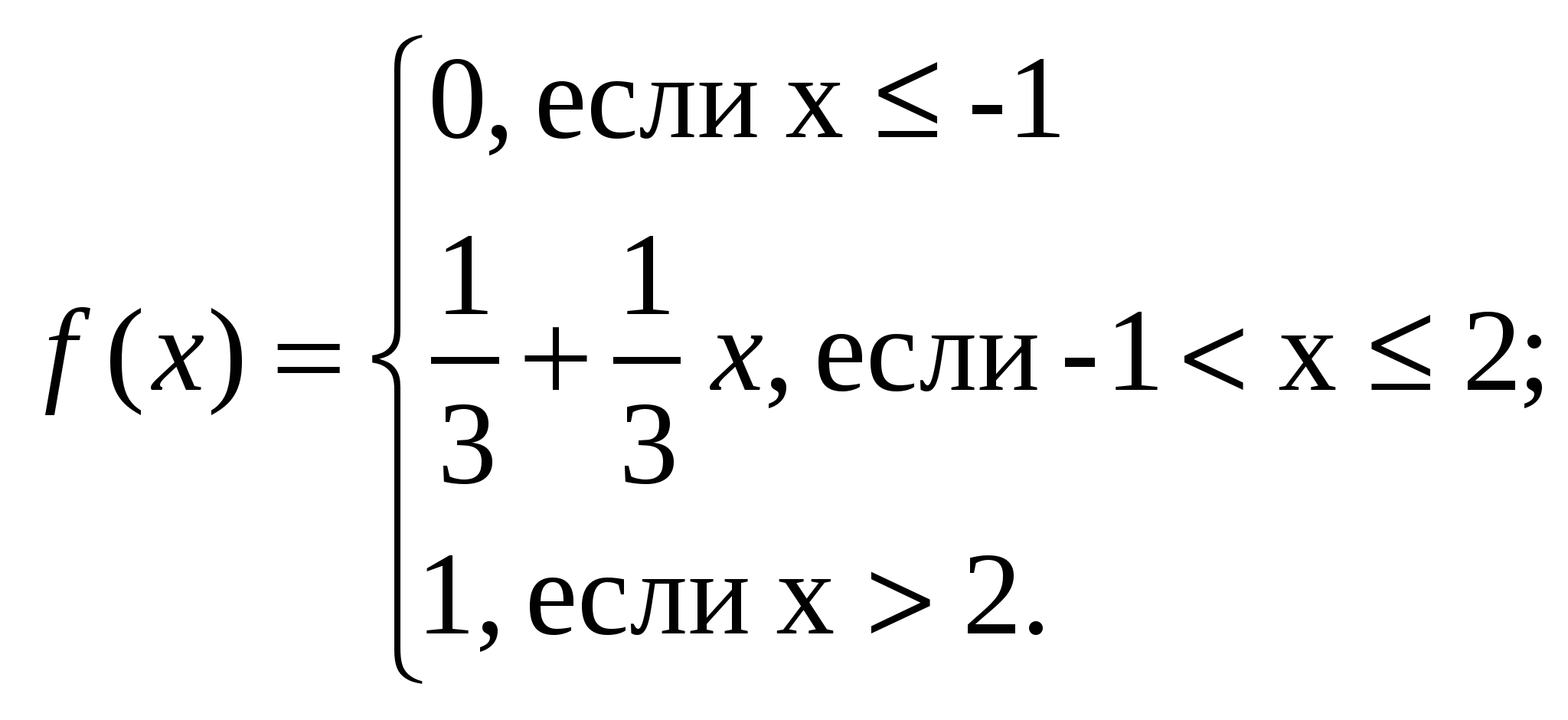 14. ВАРИАНТ 31. В 25-ти экзаменационных билетах содержатся по два вопроса, которые не повторяются. Экзаменуемый знает ответы на 45 вопросов. Какова вероятность того, что доставшийся билет состоит из подготовленных им вопросов? 2. На сборку механизма поступают детали с двух автоматов. Первый автомат в среднем даёт 1,5 % брака, второй 1%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 2000 деталей, а со второго 1500. 3. По воздушной цели производится из двух различных ракетных установок. Вероятность поражения цели первой установкой равна 0,85, второй 0,9, а вероятность поражения цели двумя установками равна 0,99. Найти вероятность поражения цели, если известно, что первая установка срабатывает с вероятностью 0,8, а вторая 0,7. 4. В одном из трёх ящиков 6 белых и 4 чёрных шарика, во втором 7 белых и 3 чёрных, в третьем только 8 белых. Наугад выбираем один из трёх ящиков и из него снова наугад выбираем один шарик. Он оказался белым. Какова вероятность того, что этот шарик вынут из второго ящика? 5. Предположим, что 6 % всех мужчин и 0,25 % всех женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина (считать, что мужчин и женщин одинаковое число). 6. По цели производится три независимых выстрела. Вероятность попадания в цель при одном выстреле равна 0,4. Для поражения цели достаточно двух попаданий. Найти вероятность поражения цели. 7. Вероятность появления события А хотя бы один раз в трёх независимых опытах равно 0,992. Какова вероятность появления события А в одном опыте, если в каждом опыте эта вероятность одинакова? 8. Вероятность изготовления изделия высшего сорта на данном предприятии равна 0,6. Чему равно наивероятнейшее число изделий высшего сорта в случайно отобранной партии из 100 изделий и вероятность этого события. 9. Вероятность того, что саженец ели прижился и будет успешно расти равна 0,8. Посажено 400 еловых саженцев. Какова вероятность того, что нормально вырастут не менее 250 деревьев? 10. С вероятностью попадания при одном выстреле 0,7 охотник стреляет по дичи до первого попадания, но успевает сделать не более 4 выстрелов. Дискретная случайная величина х числопромахов. 1) найдите закон распределения х 2) постройте многоугольник распределения. 11. 13.   14. ВАРИАНТ 4 1. Из партии, состоящей и 20 радиоприёмников, для проверки отбирают три приёмника. Партия содержит пять неисправных приёмников. Какова вероятность того, что в число отобранных войдут один неисправный и два исправных приёмника? 2. Имеются две урны: в первой 3 белых шара и 2 чёрных; во второй 4 белых и 4 чёрных. Из первой урны во вторую перекладывают, не глядя, два шара. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым. 3. На фабрике изготавливают болты, первая машина производит 25 %, вторая 35 %, третья 40 % всех изделий. В их продукции брак составляет соответственно 5, 4 и 2 %. Какова вероятность того, что случайно выбранный болт дефектный? 4. Путешественник может купить билет в одной из трёх касс железнодорожного вокзала. Вероятность того, что он направится к первой кассе 1/2, ко второй 1/3 к третьей 1/6. Вероятность того, что билетов уже нет в кассах таковы: в первой кассе 1/5, во второй 1/6, в третьей 1/6. Путешественник обратился в одну из касс и получил билет. Определите вероятность того, что он направился к первой кассе. 5. При разрыве снаряда образуются осколки трёх весовых категорий: крупные средние и мелкие, причем число крупных, средних и мелких осколков составляет соответственно 0,1, 0,3, 0,6 от общего числа осколков. При попадании в броню крупный осколок разбивает её с вероятностью 0,9, средний с вероятностью 0,2, мелкий с вероятностью 0,05. В броню попал один осколок и пробил её. Найти вероятность того, что эта пробоина причинена средним осколком. 6. В квартире 4 электролампочки. Для каждой лампочки вероятность того, что она останется исправной в течение года, равна 5/6. Какова вероятность того, что в течение года придётся заменить не меньше половины лампочек? 7. Вы играете в шахматы с равным по силе партнёром. Чего следует больше ожидать: трёх побед в четырёх партиях или 5 побед в 8 партиях? 8. Вероятность того, что данный баскетболист забросит мяч и корзину, равна 0,4. Произведено 24 броска. Найти наивероятнейшее число попаданий и соответствующую вероятность. 9. 80 % продукции объединения «Юность» - высшего сорта. Какова вероятность того, что из 10000 изделий этого объединения высшего сорта будет не меньше 6820 и не больше 7600 изделий? 10. 2 стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка при одном выстреле 0,5, для второго 0,4. Дискретная случайная величина х – число попаданий в мишень. 1). Найти закон распределения х. 2). Постройте многоугольник распределения. 11. 13.  14. |
