семестровая работа (очная форма)). Теория вероятностей методические указания и варианты заданий типового расчёта

• Название: Теория вероятностей методические указания и варианты заданий типового расчёта
• Анкор: семестровая работа (очная форма)).doc
• Дата: 02.04.2018
• Размер: 484.5 Kb.
• Имя файла: семестровая работа (очная форма)).doc
• Тип: Методические указания; #17519
• страница: 13 из 13

ВАРИАНТ 28

1. Владелец одной карточки лотереи "Спортлото" (5 из 36) зачеркивает 5 номеров. Какова вероятность того, что им будет угадано не менее 4 номеров?

2. В команде из 12 спортсменов 5 мастеров спорта. По жеребьёвке из команды выбирают 3 спортсменов. Какова вероятность того, что все выбранные спортсмены являются мастерами спорта?

3.Имеются 2 урны. В первой 1 белый и 3 чёрных, во второй 3 белых и 1 чёрный шар. Из первой и второй урн не глядя берут по два шара и перекладывают в третью. Шары в третьей урне перемешивают и берут наугад 1 шар. Найти вероятность того, что шар чёрный.

4.В группе из 20 охотников имеются 10 отличных, 6 хороших и 4 посредственных стрелков. Вероятность промаха для отличного стрелка равна 0,1, для хорошего 0,3, для посредственного 0,6. Случайно выбранные два охотника производят по одному выстрелу. Найти вероятность того, что они оба попадут в цель.

5.В группе из 25 человек, среди которых 3 отличника, 15 хорошистов, 7 троечников необходимо сдать зачёт, состоящий из 30 вопросов, причем отличник знает все вопросы, хорошист 80 %, а троечник 60 %. Вызванный наугад студент не ответил на поставленный вопрос. Какова вероятность того, что он хорошист?

6.На конкурсную комиссию были приглашены 3 доктора наук, 5 кандидатов и 7 человек, не имеющих учёной степени. Вероятность пройти комиссию для каждой из этих групп равна, соответственно, 0,98; 0,9; 0,8. Товарищ, вызванный первым, не прошел комиссию. Какова вероятность того, что это был кандидат наук?

7.Механик обслуживает 4 станка одного типа. Вероятность поломки станка в течении дня равна 0,1. Найти вероятность того, что в течении дня не менее трёх станков окажутся в рабочем состоянии.

8.10 % продукции кирпичного завода оказывается бракованной. Найти вероятнейшее число хороших кирпичей в партии из 1000 кирпичей и вероятность этого события.

9.Игральный кубик подкинули 125 раз. Какова вероятность того, что шестёрка появится не более 60 раз?

10.Написать закон распределения дискретной случайной величины х – числа появлений "герба" при двух бросаниях монеты.

11.
13. ;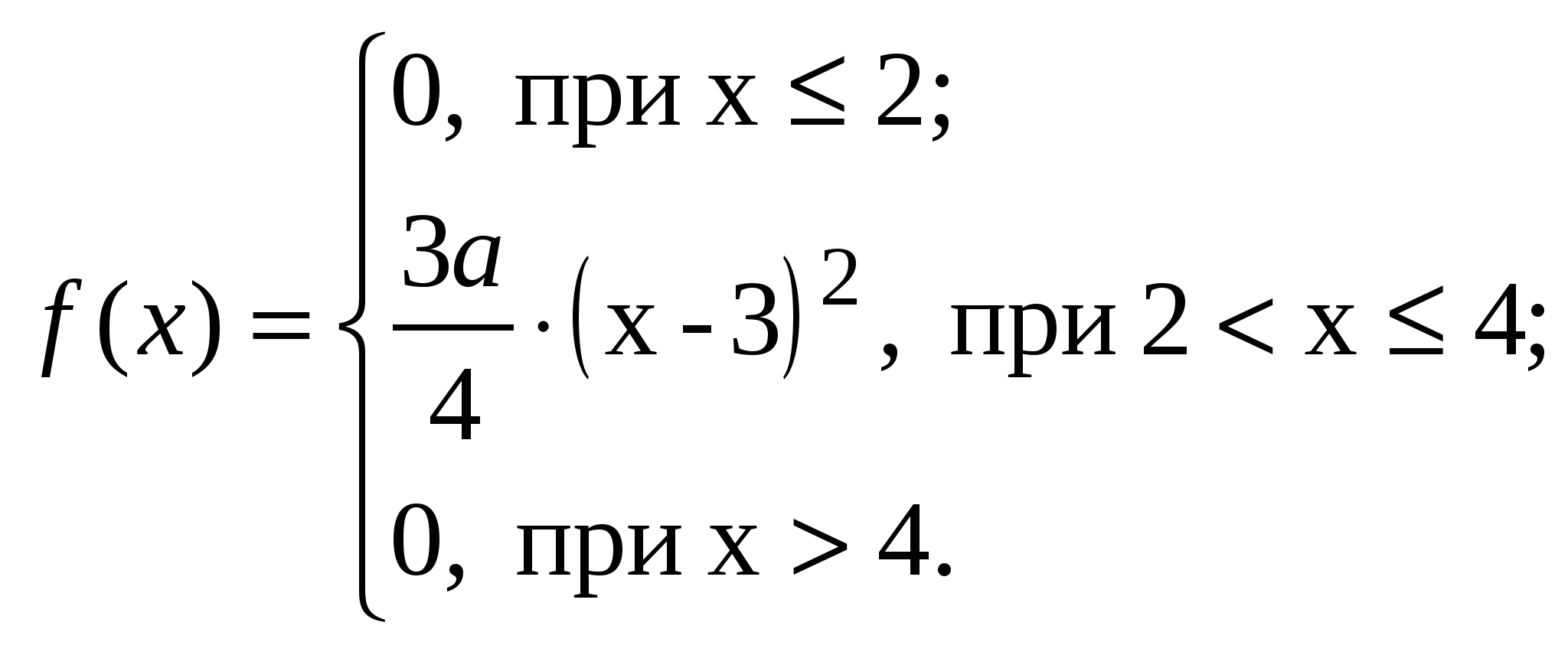
14. а=14,

Вариант 29

1.На прилавке лежат 10 кочанов капусты, среди которых 4 нестандартных. Найти вероятность того, что среди 3 отобранных продавцом кочанов будет хотя бы 1 нестандартный.

2.Вероятность попадания в мишень при одном выстреле для первого стрелка равна Р, для второго 0,7. Известно, что вероятность ровно одного попадания при одном выстреле обоих стрелков равна 0,38. Найти Р.

3.На межрайбазе находятся костюмы, изготовленные на трёх фабриках. Из них 30 % изготовлено на первой, 50 % на второй, и 20 % на третьей фабрике. Известно, что из каждых 100 костюмов, изготовленных на первой фабрике, знак качества имеют 60. Для второй и третьей фабрик этот показатель равен, соответственно, 70 и 80. Определить вероятность того, что взятый наугад с базы костюм не будет иметь знак качества.

4.Имеется 2 урны. В первой 3 белый и 1 чёрный шар, во второй 2 белых и 3 чёрных шара. Из первой урны во вторую перекладывают, не глядя, 3 шара. После этого из второй урны наугад берут 1 шар. Найти вероятность того, что этот шар будет белым.

5.В продукции кондитерской фабрики шоколадные конфеты составляют 40 % ассортимента. В среднем 10 из 1000 шоколадных конфет оказывается с браком. Для остальной продукции этот показатель равен 5 из 200. Выбранное наугад изделие оказалось без брака. Какова вероятность того, что это была шоколадная конфета?

6.Для сдачи норм ГТО из первой группы пришло 20 человек, из второй 15 и из третьей 10. Студент первой группы сдает нормы с вероятностью 0,7; второй 0,8, третий 0,9. Наудачу выбранный студент не сдал нормы ГТО. Какова вероятность того, что этот студент был из второй группы?

7.Певец получит главный приз, если он победит по крайней мере в трёх конкурсах. Найти вероятность получения им приза, если было проведено 5 конкурсов и вероятность победы певца в каждом конкурсе равна 0,7.

8.Вероятность изготовления пальто высшего качества на швейной фабрике равна 0,6. Изготовлено 600 пальто. Чему равно наивероятнейшее число изделий высшего качества и вероятность этого события?

9.10 % яблок поступающих в магазин, бракованные. Найти вероятность того, что в партии из 10000 яблок будет менее 200 бракованных.

10.Устройство состоит из 3 элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента в одном опыте равна 0,2. Составить закон распределения числа отказавших элементов в одном опыте.

11.
13.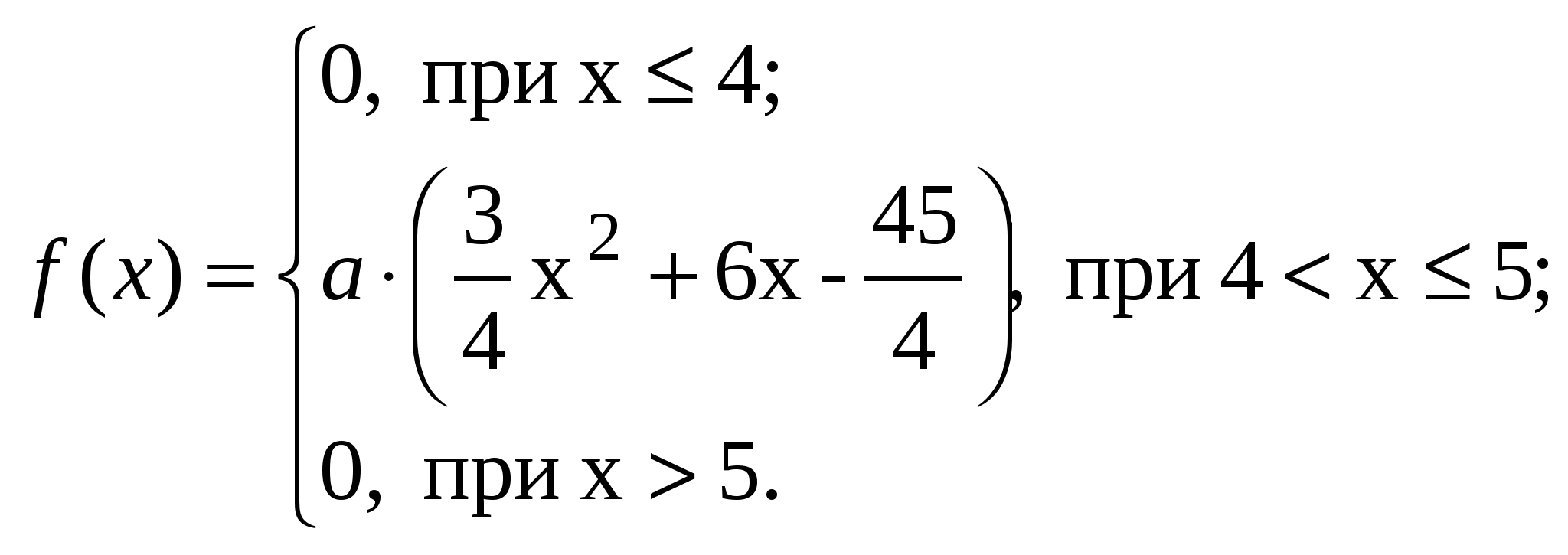
14. а = 16,

Вариант 30

1. 
   Из 4 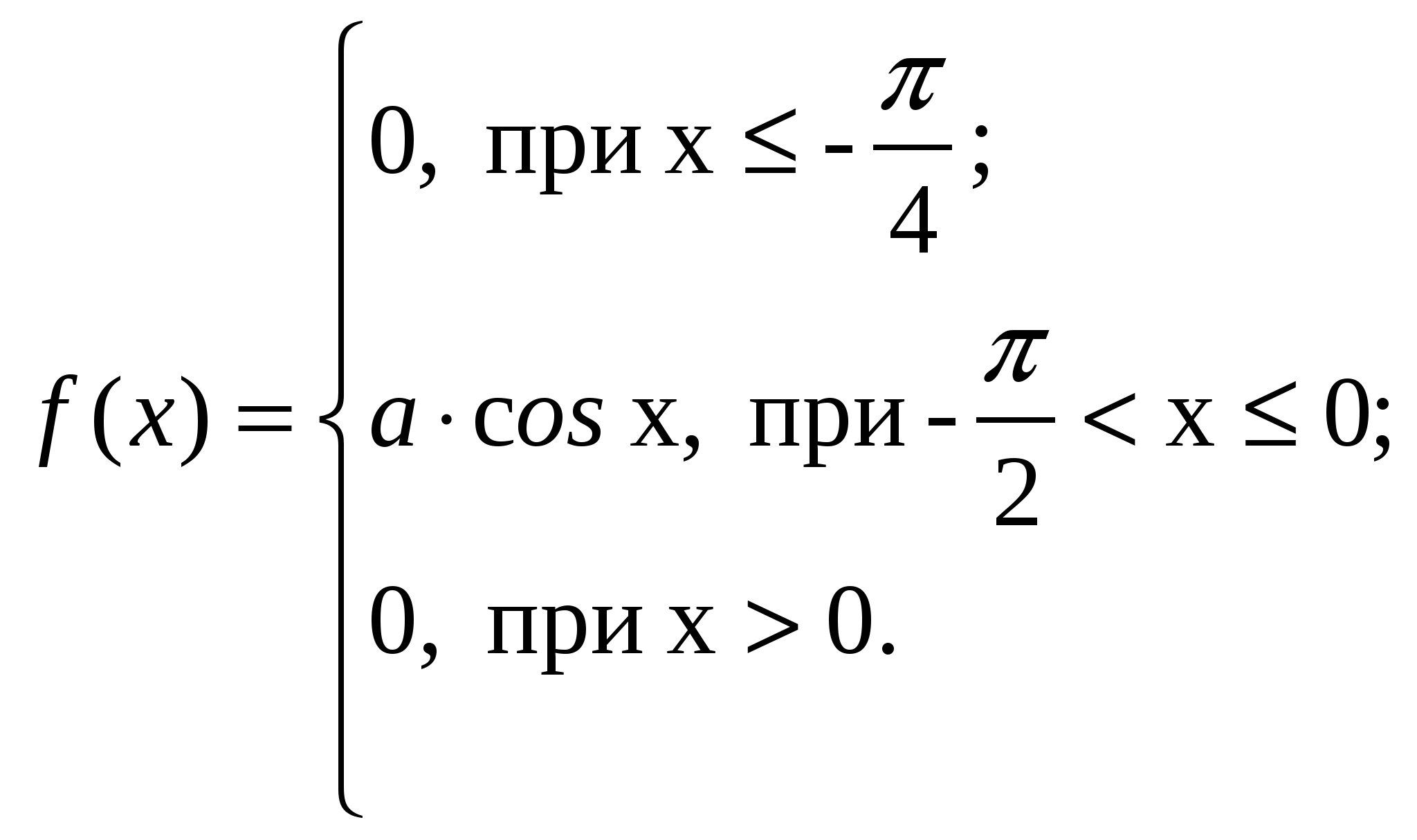лётчиков, 6 штурманов и 5 стюардесс необходимо сформировать экипаж, в который должны войти 2 лётчика, 1 штурман и 3 стюардессы. Сколькими способами это можно сделать?
   
2. 
   Экзаменационный билет содержит 3 вопроса. Вероятность того, что студент ответит на первый и второй вопросы билета, равны 0,9; на третий 0,8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса.
   
3. 
   Вероятность хотя бы одного попадания в цель при 4 независимых выстрелах равна 0,9984. Найти вероятность попадания при одном выстреле.
   
4. 
   На заводе, изготавливающем шайбы, первый автомат производит 23 %, второй 37 % и третий 40 % всех шайб. В их продукции доля стандартных изделий составляет, соответственно, 85, 90 и 95 %. Какова вероятность того, что выбранная шайба будет бракованная?
   
5. 
   Имеется 2 одинаковых ящика с шарами. В первом ящике 2 белых, 3 чёрных и 5 красных шаров. Во втором 3 белых, 5 чёрных и 2 красных шара. Наудачу выбирают 1 ящик и вынимают из него шар. Какова вероятность того, что вынутый шар не белый?
   
6. 
   Завод выпускает для магнитофонов 3 типа предохранителей. Доля каждого из них в общем объёме составляет 30, 50 и 20 %. При перегрузке сети предохранитель первого типа срабатывает с вероятностью 0,8, второго 0,9 и третьего 0,85. Выбранный наудачу предохранитель не сработал при перегрузке сети. Какова вероятность того, что он принадлежал к первому типу?
   
7. 
   Каждому из 3 первоклассников – Пете, Коле и Мише, предложено одинаковое количество загадок. Петя отгадывает в среднем 3 загадки из 4, Коля 5 из 6 и Миша 9 из 10. Наугад выбранный школьник не отгадал загадку. Какова вероятность того, что это был Коля?
   
8. 
   Игральная кость подброшена 5 раз. Найти вероятность того, что по крайней мере, 3 раза появится шестёрка.
   
9. 
   В партии товаров 400 изделий. Вероятность того, что изделие будет высшего сорта равна 0,8. Какова вероятность того, что число изделий высшего сорта будет от 310 до 330?
   
10. 
    В партии из 6 деталей имеется 4 стандартные Наудачу отобраны 3 детали. Составить закон распределения случайной дискретной величины х – число стандартных деталей среди отобранных
    

11.
13.
14. а = 16,

Литература.

1. 
   Солодовников А. С. Теория вероятностей.- М.: Просвещение, 1983.
   
2. 
   ГмурманВ. Е. Теория вероятностей и математическая статистика. -М.: Высшая школа, 1978,
   
3. 
   Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистики. -М.: Высшая школа, 1979.
   
4. 
   Ивашов – Мусатов О. С. Теория вероятностей и математическая статистика. -М.: Наука, 1979.
   

ОГЛАВЛЕНИЕ:

Введение		3
Программа курса		3
1. Раздел «Теория вероятностей»		3
2. Задания потового расчета		3
3. Типовой расчет		4
Вариант № 1		4
Вариант № 2		6
Вариант №3		7
Вариант № 4		8
Вариант № 5		10
Вариант № 6		11
Вариант № 7		12
Вариант № 8		14
Вариант № 9		15
Вариант № 10		16
Вариант № 11		17
Вариант № 12		19
Вариант № 13		20
Вариант № 14		22
Вариант № 15		23
Вариант № 16		24
Вариант № 17		26
Вариант № 18		27
Вариант № 19		29
Вариант № 20		30
Вариант № 21		31
Вариант № 22		33
Вариант № 23		34
Вариант № 24		35
Вариант № 25		37
Вариант № 26		38
Вариант № 27		39
Вариант № 28		40
Вариант № 29		42
Вариант № 30		43
Литература		44