семестровая работа (очная форма)). Теория вероятностей методические указания и варианты заданий типового расчёта
 Скачать 484.5 Kb. Скачать 484.5 Kb.
|
ВАРИАНТ 221. На самолёт требуются три стюардессы, которых выбирают по жребию из 20 девушек. 7 из них блондинки, остальные брюнетки. Какова вероятность того, что среди выбранных трёх стюардесс будет, по крайней мере, одна блондинка и, по крайней мере, одна брюнетка? 2 Слово «стол», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекаются одна за другой три буквы. Какова вероятность того, что при этом появится слово «сто»? 3. В двух ящиках находятся шары: в одном 4 белых и 2 чёрных, в другом 2 белых и 3 чёрных. Из первого во второй переложены три шара. Какова вероятность вынуть из второго ящика чёрный шар? 4. На двух станках изготавливаются одинаковые детали. Вероятность изготовления детали высшего качества на первом станке равна 0,92, на втором 0,8. Изготовленные детали находятся на складе. Среди них деталей, изготовленных на первом станке, в 3 раза больше, чем на втором. Определить вероятность того, что наудачу взятая деталь произведена на первом станке и высшего качества. 5. На фабрике, изготовляющей некоторую продукцию, первая машина производит 30 %, вторая 45 %, третья 25 % всех изделий. Брак их продукции составляет соответственно 2 %, 5 %, и 3 %. Найти вероятность того, что случайно выбранное изделие произведено первой машиной, если оно оказалось дефектным. 6. Предположим, что 20 % мужчин и 40 % женщин блондины. Наугад выбранное лицо оказалось блондином. Какова вероятность того, что это женщина (считать количество мужчин и женщин одинаковым)? 7. Вероятность хотя бы одного попадания при двух выстрелах равна 0.64. Найти вероятность 3 попаданий при пяти выстрелах. 8. Известно, что 3/5 всего числа изготовленных заводом телефонных аппаратов является продукцией первого сорта. Чему равна вероятность того, что в изготовленной партии из 150 аппаратов окажется наивероятнейшее число аппаратов первого сорта? 9. В результате проверки качества приготовленного для посева зерна установлено, что 90 % зёрен всхожи. Найти вероятность того, что среди отобранных 900 зёрен прорастет от 600 до 640 штук. 10. На пути движения автомобиля 5 светофоров, каждый из них или разрешает или запрещает дальнейшее движение с вероятностью 0,5. Найдите закон распределения случайной величины х, равной числу светофоров, пройденных автомобилем до первой остановки. 11. 13. 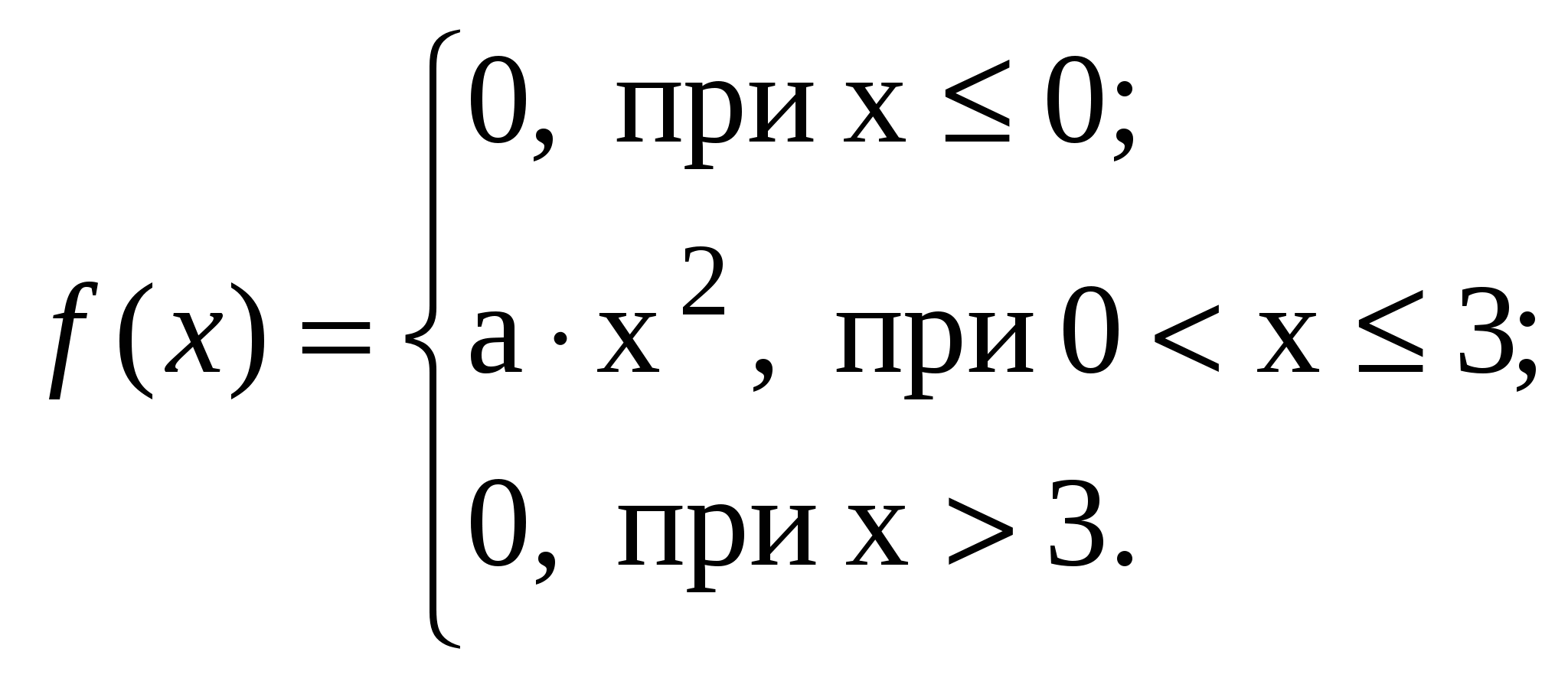 14. а = 7, ВАРИАНТ 23 1. Ящик содержит 10 деталей, среди которых 2 стандартных. Найти вероятность того, что в наудачу отобранных 6 деталях окажется не более одной стандартной. 2. На каждой из восьми одинаковых карточках напечатана одна из следующих букв: о, м, р, п, т, с, к. Карточки тщательно перемешаны. Найти вероятность того, что на четырёх вынутых по одной расположенных в одну линию карточках можно будет прочесть слово «трос». 3. В один прекрасный весенний вечер Дюпон и Дюран играли в кости на террасе кофе. Они по очереди бросали две кости. Если сумма оказывалась равной семи, то очко выигрывал Дюран, а если сумма равнялась восьми, то выигрывал Дюпон. На кого из них вы бы поставили, если нам пришлось бы держать пари? 4. На склад поступают одинаковые электрические утюги. Первый завод поставляет 80 %; второй 20 % всей продукции. Известно, что первый завод выпускает 90 % продукции первого сорта, второй 95 %, Какова вероятность того, что проданный покупателю утюг из наудачу выбранной партии первого сорта? 5. В группе спортсменов 30 бегунов, 10 боксёров и 20 лыжников. Вероятности выполнить норму такова: для бегуна 0,9, для боксёра 0,6, для лыжника 0,7. Найти вероятность того, что спортсмен, выбранный наудачу, выполнил норму. 6. В некоторой отрасли 30 % продукции производится фабрикой №1, 25 % фабрикой № 2, а остальные фабрикой № 3. На фабрике № 1 в брак идет 1 % всей продукции, на фабрике № 2 1,5 %, на фабрике №3 2 %. Взятая наудачу деталь оказалась стандартной. Какова вероятность того, что она произведена фабрикой № 2? 7. Игральная кость бросается 5 раз. Найти вероятность того, что два раза появится число очков, кратное трём. 8. Автоматическая штамповка клемм для предохранителей даёт 10 % отклонений от принятого стандарта. Сколько стандартных клемм следует ожидать с вероятностью 0,0587 среди 400 клемм. 9. В деревне проживают 100 человек. Вероятность того, что любой из них зайдёт в сельпо, равна 0,8. Найти вероятность того, что в течение дня в сельпо зайдёт не менее 10 человек. 10. В партии деталей 10 % нестандартных. Наудачу отобраны 4 детали. Составить закон распределения дискретной случайной величины х – числа нестандартных деталей среди 4 отобранных. Построить многоугольник полученного распределения. 11. 13. 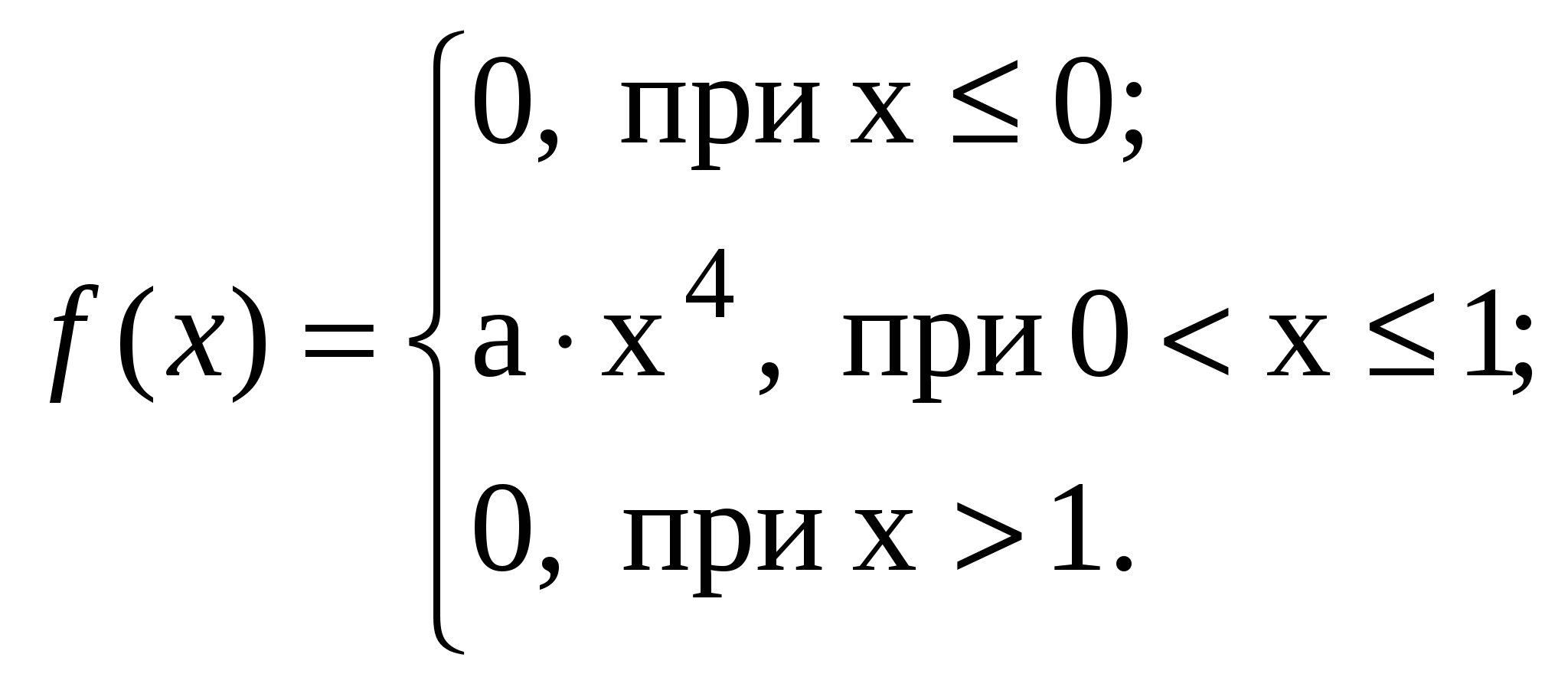 14. а = 7, |
