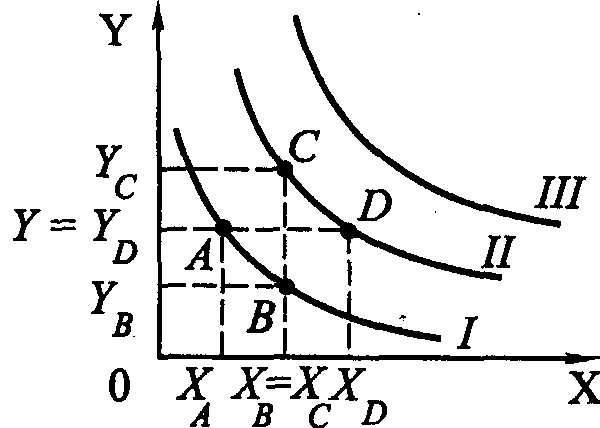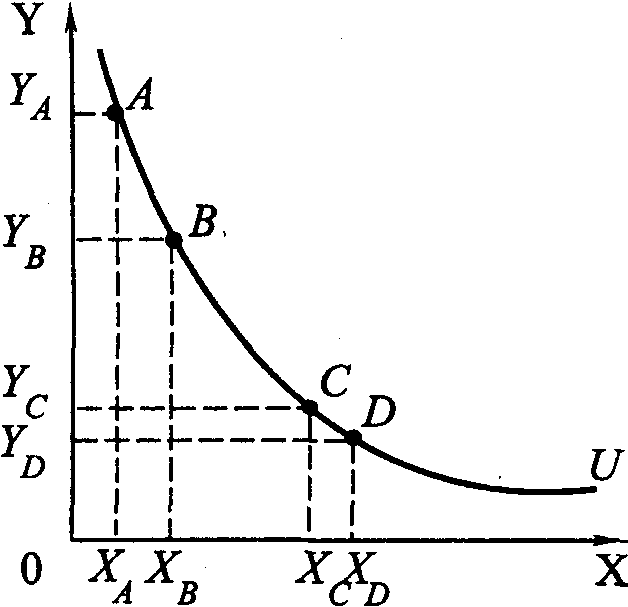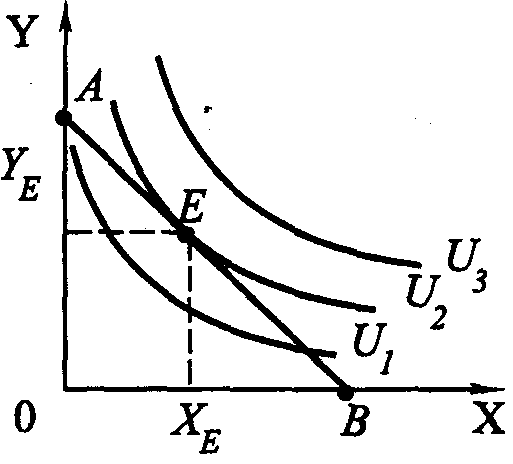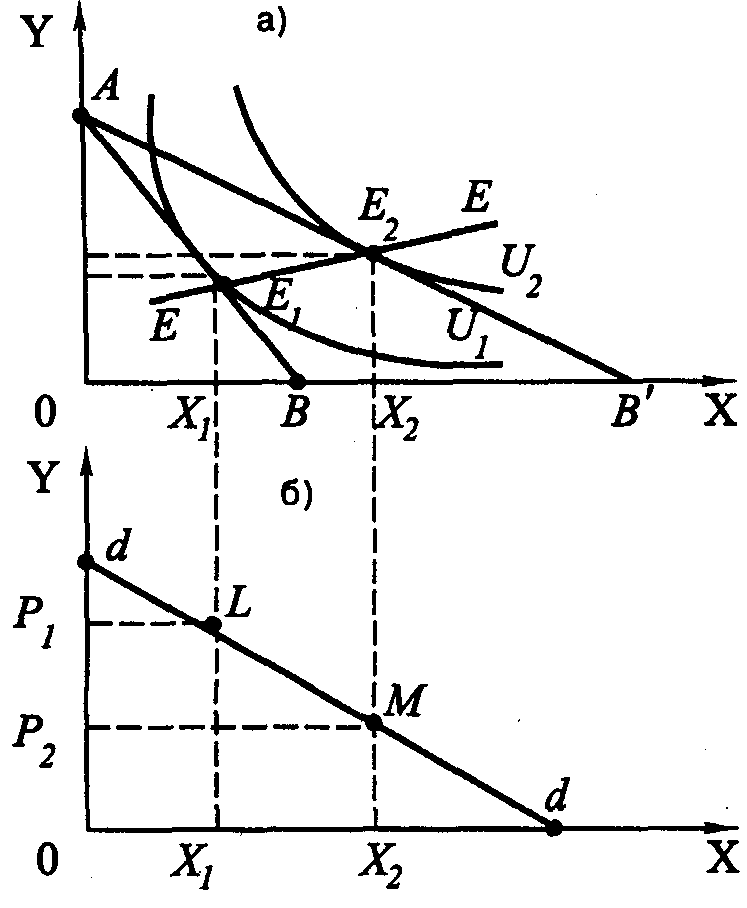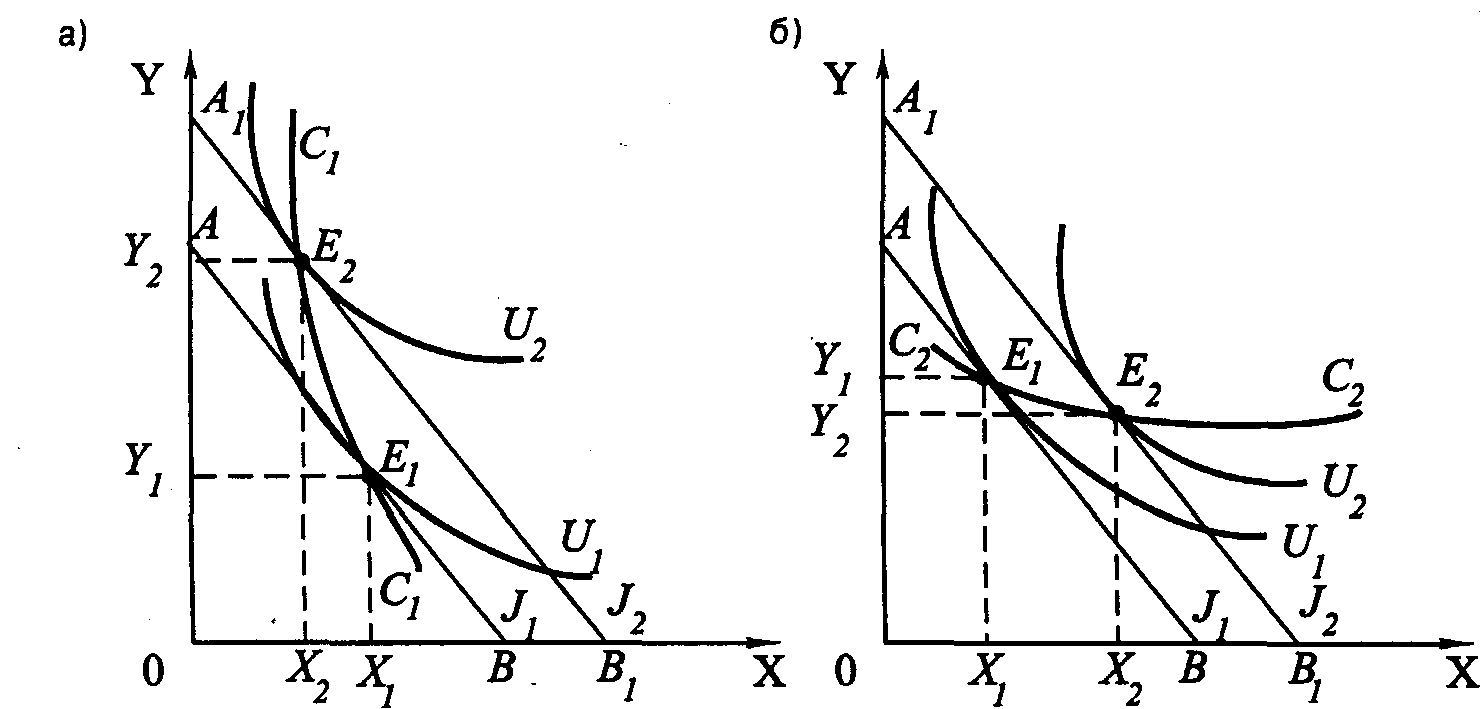1.2.1. АКСИОМЫ ПОРЯДКОВОГО ПОДХОДА
Порядковый подход к анализу полезности и спроса в основе своей опирается на ту же теоретическую базу, что и количественный подход, поскольку он не отвергает ни один закон, положенный в основу количественного подхода. Принципиальная особенность порядкового подхода состоит в том, что он вообще не требует от потребителя измерения уровня полезности благ в каких-либо единицах и ограничивается лишь способностью потребителя упорядочивать различные блага, представленные в виде соответствующих наборов, с позиции их «предпочтительности». Порядковый подход опирается на следующие аксиомы.
1. Аксиома полной упорядоченности
Эта аксиома исходит из того, что потребитель в результате сравнения одного набора благ с другим всегда может сказать, какой из них для него является предпочтительным или они оба равноценны. В порядковом подходе вместо слова «равноценность» обычно употребляется слово «безразличность».
Свои суждения по поводу конкретных наборов благ потребитель фиксирует с помощью определенных символов, выражающих либо предпочтение (>), либо безразличие (). Так, если потребитель считает, что набор А для него является более предпочтительным, нежели набор В, то он выразит это следующей записью: А>В. Если же оба набора для него равноценны, то запись будет иметь такой вид: А
В.
2. Аксиома транзитивности
С помощью этой аксиомы осуществляется упорядочение (с точки зрения предпочтения или безразличия) уже не двух, а большего числа наборов благ. Так, если потребитель в результате изучения трех наборов благ А, В, С расставил их следующим образом: А>В и В>С, то можно сказать, что набор А в данном случае для него предпочтительнее набора С (А>С).
Если же, по мнению потребителя, АВ и ВС, то отсюда можно сделать вывод, что для него наборы А и С являются также равноценными (АС).
3. Аксиома ненасыщения
Если два набора благ отличаются друг от друга лишь количеством единиц одного какого-то блага, то потребитель всегда предпочтет тот набор, в котором этого блага больше.
4. Аксиома независимости потребителя
Степень удовлетворения потребителя зависит только от количества потребляемых им благ и не зависит от количества благ, потребляемых другими потребителями. Это значит, что в данном случае не принимаются в расчет чувства зависти и сострадания.
Содержание аксиом свидетельствует, что порядковая теория полезности действительно не ориентирована на непосредственное, прямое измерение уровня полезности наборов благ. Оценка их полезности здесь осуществляется косвенным путем, на основе выявления предпочтения. Поэтому, если потребитель считает, что набор А для него более предпочтителен, чем набор В, то отсюда можно сделать вывод, что, с точки зрения потребителя, набор А обладает большей полезностью, нежели набор В. Вопрос о соотношении уровней полезности наборов (на сколько или во сколько раз набор А полезнее набора В) при этом не ставится.
Поэтому и задачу максимизации полезности порядковая теория трактует как задачу выбора потребителем такого набора благ, который бы, с одной стороны, был наиболее предпочтительным, а с другой – по своей стоимости не превосходил бюджета потребителя.
Дальнейшее рассмотрение будет вестись только применительно к наборам, состоящим из двух благ – Х и Y, поскольку такие наборы легко вписываются в систему плоскостных координат. Полученные выводы могут быть распространены и на любые другие наборы.
1.2.2. КРИВАЯ БЕЗРАЗЛИЧИЯ И ЕЕ АНАЛИЗ
Основную сложность в порядковом подходе представляет построение кривых безразличия. Каждая кривая безразличия объединяет множество равнополезных (равноценных), разумеется, с точки зрения конкретного потребителя, наборов благ. Следовательно, прежде чем строить такие кривые, необходимо образовать группы равнополезных наборов. Поскольку все наборы, включенные в одну группу, связаны друг с другом знаком безразличия (), то и кривая, объединяющая местоположения этих наборов в системе координат Х и Y, также называется кривой безразличия.
Если нанести на поле координат столько кривых безразличия, сколько возможно, получим карту безразличия.
На рис 1.8 показаны три кривые безразличия. На первой и второй кривой безразличия показаны по два товарных набора. Набор А содержит ХA единиц товара Х и YA единиц товара Y. Набор В включает XB единиц товара Х и YB единиц товара Y. Поскольку точки А и В находятся на одной и той же кривой безразличия I, то наборы А и В следует рассматривать как равноценные (равнополезные) для того потребителя, для которого построены эти кривые безразличия.
Обращает на себя внимание набор С. Он содержит наибольшее количество единиц товара Y (Yc) и столько же, сколько набор В, единиц товара Х (Хc). В соответствии с третьей аксиомой товарный набор С предпочтительнее набора В, а следовательно, и набора А. Поскольку точки С и D лежат на одной и той же кривой безразличия II, то это значит, что наборы С и D для данного потребителя являются равноценными. Кривые безразличия обладают рядом свойств, важнейшими из которых являются следующие:
А. Кривая безразличия, лежащая выше и правее другой кривой безразличия, выражает более предпочтительные для данного потребителя наборы товаров. Справедливость такого утверждения была показана при рассмотрении рис. 1.8.
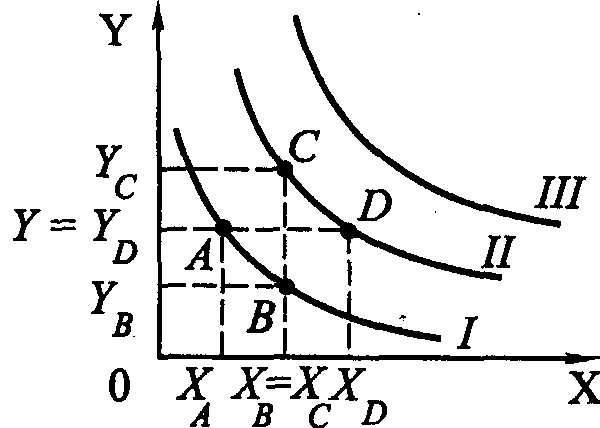
Рис. 1.8. Кривые безразличия
Б. Кривые безразличия никогда не пересекаются. В противном случае это противоречило бы свойству А.
В. Кривые безразличия имеют отрицательный наклон. Это также вытекает из свойства А.
1.2.3. ПРЕДЕЛЬНАЯ НОРМА ЗАМЕНЫ
Поскольку все товарные наборы, расположенные на одной и той же кривой безразличия, являются для данного потребителя равноценными, а следовательно, взаимозаменяемыми, то и те два товара, которые образуют эти наборы, также должны быть для потребителя в определенной степени взаимозаменяемыми.
Количественным показателем такой взаимозаменяемости является предельная норма замены.
Предельная норма замены блага Y благом Х (MRSxy) показывает, каким количеством блага Y следует поступиться ради увеличения в наборе блага Х на единицу при условии сохранения полезности набора на прежнем уровне:
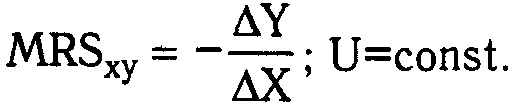 (1.15) (1.15)
На рис. 1.9 показано, что переход от товарного набора А к товарному набору В связан с увеличением блага Х на одну единицу (XB - ХA= 1), что, в свою очередь, требует сокращения блага Y на ΔY единиц (YB - YA), чтобы сохранить полезность набора В на уровне полезности набора А.
Более точное исчисление предельной нормы замены обеспечивается с помощью следующей формулы:
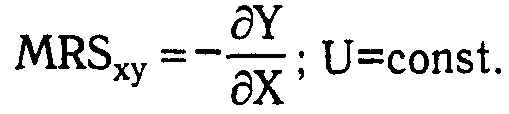 (1.16) (1.16)
Поскольку при последовательном увеличении содержания в наборе блага Х на одну единицу величина DY с каждым разом становится все меньше и меньше (рис. 1.9), то отсюда можно сделать вывод, что убывание предельной нормы замены имеет в принципе тот же смысл, что и убывание предельной полезности в количественной теории.
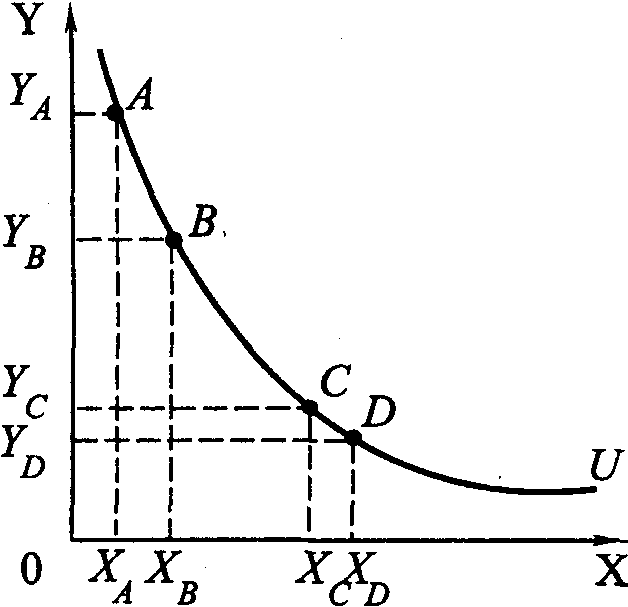
Рис.1.9. Определение DX и DY для исчесления MRSxy
Различие заключается лишь в методах оценки полезности благ. В количественной теории полезности для этой цели были предложены ютилы, в порядковой теории полезность каждой дополнительной единицы блага оценивается косвенным путем – количеством единиц другого блага, которым потребитель согласен пожертвовать.
Предельная норма замены как раз и выражает то количество единиц другого блага, которым необходимо пожертвовать. С учетом сказанного выше можно записать:
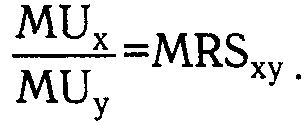 (1.17) (1.17)
1.2.4. БЮДЖЕТНЫЕ ОГРАНИЧЕНИЯ
Как уже отмечалось ранее, каждый рациональный потребитель стремится максимизировать совокупную полезность, которую он получает за счет своего бюджета.
Если в количественной теории потребитель свои вкусы и предпочтения выражает в виде системы показателей предельной полезности благ и графиков MU и TU, то в порядковой теории в качестве средства выражения системы предпочтений потребителя выступает карта безразличия. При этом потребитель знает, что самые предпочтительные наборы находятся на наиболее удаленной от начала координат кривой безразличия. Но «дотянуться» до такой кривой безразличия потребитель, как правило, не может. Этому мешает недостаточность его бюджета.
Все доступные конкретному потребителю товарные наборы могут быть выражены с помощью его бюджетной линии, если ее поместить в ту же систему координат, в которой находятся кривые безразличия.
Для построения бюджетной линии необходимо иметь уравнение этой линии. Его обоснование происходит следующим образом.
Пусть месячный доход потребителя составляет I (руб.). Предположим далее, что потребитель весь свой доход тратит на приобретение только двух товаров Х и Y.
Его бюджетное ограничение в этом случае может быть представлено в виде следующего равенства:
I = Px X + Py Y. (1.18)
Смысл бюджетного ограничения, как видим, сводится к тому, что расходы потребителя на приобретение товаров Х и Y не могут превышать его дохода. Уравнение бюджетной линии выводится непосредственно из равенства (1.14). Оно имеет следующий вид:
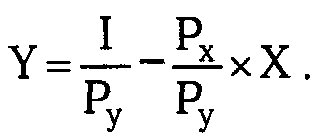 (1.19) (1.19)
На рис. 1.10 бюджетная линия изображена в виде отрезка АВ. Поскольку бюджетная линия всегда представляет собой прямую, пересекающую оси координат, то для ее построения может быть применен более простой метод. Достаточно найти лишь точки пересечения бюджетной линии с осями координат (то есть точки А и В) и соединить их прямой линией. Полученная прямая и является как раз бюджетной линией.
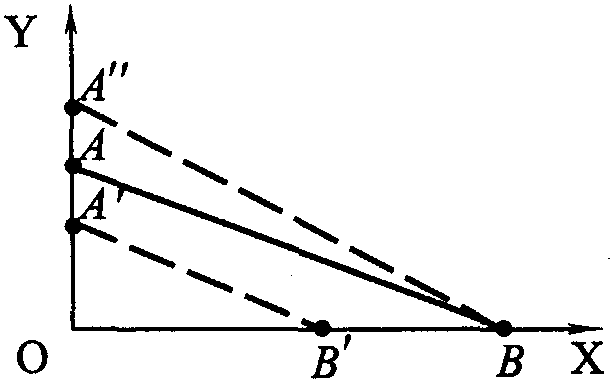
Рис. 1.10. Бюджетная линия
Положение точки А определяется длиной отрезков ОА, а положение точки В – длиной отрезка OВ. Каждый из этих отрезков соответствует количеству единиц товара Y или товара X, которое может приобрести потребитель, потратив весь свой доход только на этот товар. В связи с этим длина отрезка ОА соответствует I / Py , а длина отрезка OB – 1/Рx. В свою очередь, наклон бюджетной линии равен коэффициенту при Х в уравнении (1.19), то есть Рх / Ру.
Все наборы из товаров Х и Y, расположенные на бюджетной линии, по своей стоимости четко соответствуют доходу потребителя I, а значит, являются доступными для него. К числу доступных относятся также все товарные наборы, расположенные ниже бюджетной линии. Стоимость каждого из них ниже I. Зато все наборы, находящиеся выше бюджетной линии, стоят больше I и потому являются недоступными для данного потребителя.
1.2.4.1. Изменения в доходе и ценах
Анализируя уравнение бюджетной линии (1.19), можно сделать вывод, что ее положение зависит как от дохода потребителя, так и от цен товаров. Если бы доход потребителя оказался меньше, а цены прежними, то в этом случае бюджетная линия сместилась бы вниз (А'В'). При этом она была бы параллельна линии АВ, так как коэффициент Рx / Рy остался бы прежним. Если бы доход потребителя и цена товара Х оставались неизменными, а цена товара Y снизилась, то бюджетная линия в этом случае заняла бы положение А"В. Перемещение левого конца бюджетной линии из точки А в точку А" произошло бы потому, что отношение I / Py в данной ситуации стало больше.
1.2.5. РАВНОВЕСИЕ ПОТРЕБИТЕЛЯ
Нетрудно догадаться, что произойдет с бюджетной линией при повышении Ру, повышении или снижении Рx.
На рис. 1.11 карта безразличия индивидуума совмещена с его бюджетной линией.
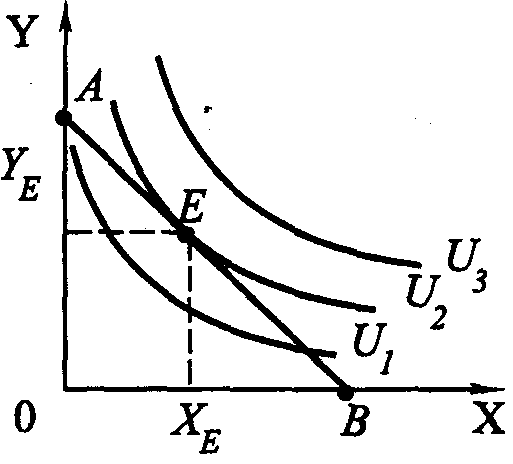
Рис. 1.11. Оптимум потребителя
Спрашивается, какой товарный набор выберет потребитель? Разумеется, тот, который расположен на наиболее удаленной кривой безразличия. Среди всех доступных ему товарных наборов, расположенных в границах треугольника ОАВ, указанному требованию отвечает набор Е, находящийся в точке, где бюджетная линия АВ лишь касается кривой безразличия U2.
Конечно, для потребителя более привлекательными являются товарные наборы, расположенные на кривой безразличия U3. Однако ограниченные размеры бюджета не позволяют ему «дотянуться» до этой кривой безразличия.
Товарный набор Е для данного потребителя является оптимальным, поскольку он наиболее предпочтителен среди всех наборов, находящихся в границах треугольника ОАВ, представляющего реально доступную для данного потребителя область.
Набор Е содержит, как видно на рис. 1.11, XE единиц товара Х и YE единиц товара Y. В точке Е наклоны бюджетной линии АВ и кривой безразличия U2 совпадают.
Поэтому применительно к точке оптимума потребителя можно записать:
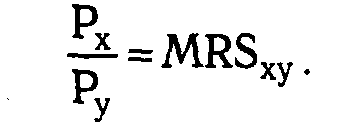 (1.20) (1.20)
Равенство (1.20) следует понимать как свидетельство достижения потребителем наиболее предпочтительного, а, следовательно, наиболее полезного товарного набора при заданном бюджете. В связи с этим можно сказать, что равенство (1.20), выражающее условие, при котором потребитель достигает своего оптимума, в принципе тождественно равенству (1.14) в количественной теории. Для доказательства данного утверждения воспользуемся равенством (1.17):
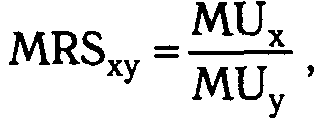
С учетом этого равенства (1.20) можно записать:
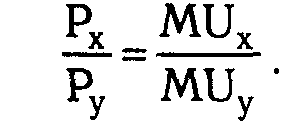 (1.21) (1.21)
После преобразования равенства (1.21) условие оптимума потребителя получает следующее выражение:
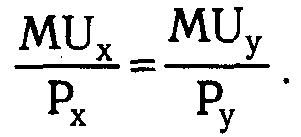 (1.22) (1.22)
Как видим, формула (1.22) тождественна уравнению (1.14).
1.3. РЕАКЦИЯ ПОТРЕБИТЕЛЯ НА ИЗМЕНЕНИЕ ЦЕН
1.3.1. КРИВАЯ «ЦЕНА-ПОТРЕБЛЕНИЕ»
Реакция потребителя на изменение дохода и цен обычно рассматривается под углом зрения изменения его спроса. Что касается системы предпочтений потребителя, а значит, и его карты безразличия, то они находятся, как правило, вне сферы влияния данных факторов. Остановимся вначале на анализе реакции потребителя на изменение цен. Его доход при этом остается неизменным.
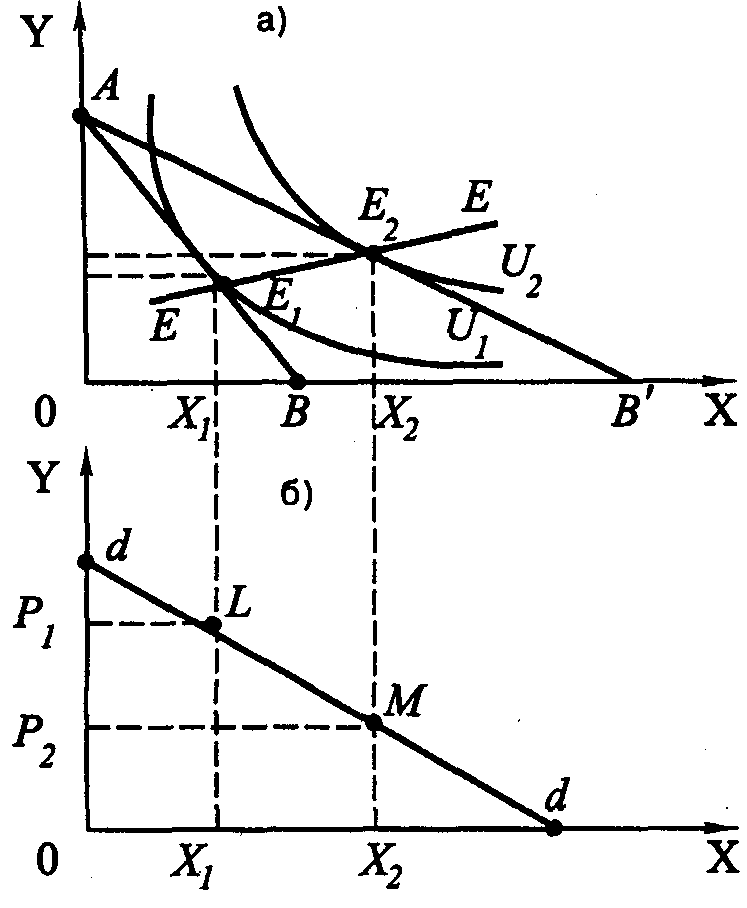
Рис. 1.12. Линия «цена-потребление» и линия индивидуального спроса
На рис 1.12, а показано смещение оптимума потребителя из точки E1 в точку E2 в результате снижения цены товара Х с Рx' до Рx". Снижение Px предопределило поворот бюджетной линии АВ против часовой стрелки вокруг точки А. В результате этого, бюджетная линия заняла новое положение АВ' и стала касаться в точке E2 более удаленной кривой безразличия U2. В связи с этим товарный набор E2 стал доступен данному потребителю.
Если соединить одной линией все точки оптимума потребителя, получаемые в результате как снижения, так и повышения Рx, то получим кривую «цена–потребление» (линия ЕЕ). Она выражает множество оптимальных сочетаний (наборов) товаров Х и Y, которые возникают при изменении цены товара X.
С помощью кривой «цена–потребление» можно построить линию индивидуального спроса данного потребителя. Здесь важно заметить, что определение линии индивидуального спроса в этом случае осуществляется исключительно на основе принципа заданности рыночных цен.
Поэтому построить линию спроса на новое благо, цена которого на данном этапе еще не известна, с помощью рассматриваемого метода невозможно. На рис. 1.12, б представлена линия индивидуального спроса dd на товар X. Она построена с помощью двух точек L и М, каждая из которых определена исходя из заданной цены и объема спроса, определенного с учетом оптимума потребителя (E1 и E2). Линия, проведенная через эти точки (L и М), рассматривается в качестве кривой индивидуального спроса на товар X. Здесь важно также обратить внимание на следующее обстоятельство. Поскольку цена спроса, как было показано в разделе 1.1, имеет отношение не к предельной, а к средней полезности, то и рыночные цены, используемые при построении кривой индивидуального спроса, не могут отличаться по своей природе от цен спроса.
1.3.2. ЭФФЕКТ ЗАМЕНЫ И ЭФФЕКТ ДОХОДА
1.3.2.1. Эффект замены и дохода для качественных товаров
Изменение цены какого-либо товара оказывает влияние на объем спроса на него двумя способами. Во-первых, посредством изменения соотношения цен, что приводит к смещению спроса с одних товаров на другие (с относительно дорогих на относительно дешевые) и, во-вторых, посредством изменения покупательной способности или реального дохода потребителя, когда рост или снижение реального дохода индивидуума в результате изменения цены данного товара приводит соответственно к росту или снижению спроса на этот товар, впрочем, как и на другие товары.
Изменение объема спроса, достигнутое с помощью первого способа, называется эффектом замены, а с помощью второго способа – эффектом дохода. При этом предполагается, что оба эффекта возникают в условиях стабильности денежного дохода потребителя и цен всех других товаров, кроме рассматриваемого. Существуют две точки зрения относительно того, как следует делить общий эффект изменения цены (в качестве которого выступает изменение объема спроса) на эффект замены и эффект дохода. Одна из них принадлежит английскому экономисту Дж. Хиксу, а другая – русскому математику и экономисту Е. Слуцкому.
Хикс полагал, что для выполнения этой процедуры необходимо воспользоваться вспомогательной бюджетной линией А'В" (рис. 1.13). Ее следует провести таким образом, чтобы она, во-первых, была параллельна бюджетной линии АВ' и, во-вторых, являлась касательной к исходной кривой безразличия U1.
Это означает, что с помощью такой вспомогательной бюджетной линии обеспечивается сохранение, с одной стороны, нового соотношения цен, а с другой – первоначального уровня удовлетворения индивидуума.
Полученная точка вспомогательного оптимума E3 позволяет разделить общий прирост спроса на товар X, вызванный снижением его цены, на эффект замены и эффект дохода. Общий прирост спроса соответствует отрезку X1X2. Точка Х3 делит его на эффект замены (отрезок Х1Х3) и эффект дохода (отрезок Х1X3). Формирование эффекта замены происходит при сдвиге оптимума потребителя из точки E1 в точку Е3 вдоль кривой безразличия U1. Это позволяет сделать вывод, что на данном участке реальный доход индивидуума остается неизменным, поскольку здесь сокращение спроса на товар Y (ввиду того, что он относительно товара Х стал дороже) компенсируется увеличением спроса на товар X.
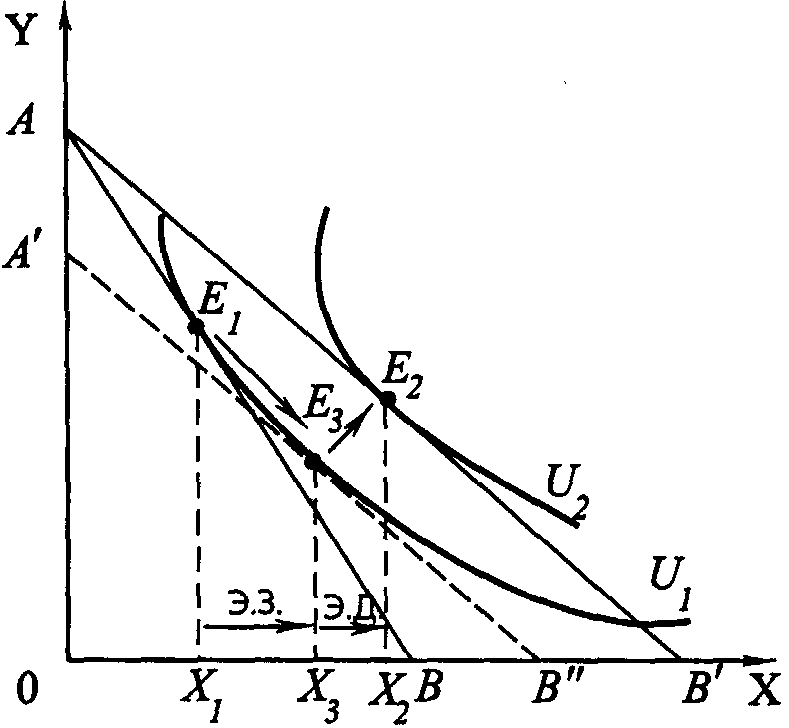
Рис. 1.13. Эффект замены и эффект дохода по Хиксу. Цена товара Х снижается
Эффект дохода формируется в процессе сдвига оптимума из точки E3 в точку E2. Особенность этого участка состоит в том, что здесь осуществляется переход с одной кривой безразличия на другую (с U1 на U2). А такой скачок потребитель может совершить лишь в условиях роста его реального дохода, что, естественно, и обеспечивает дополнительное увеличение спроса на товар X, как, впрочем, и на товар Y.
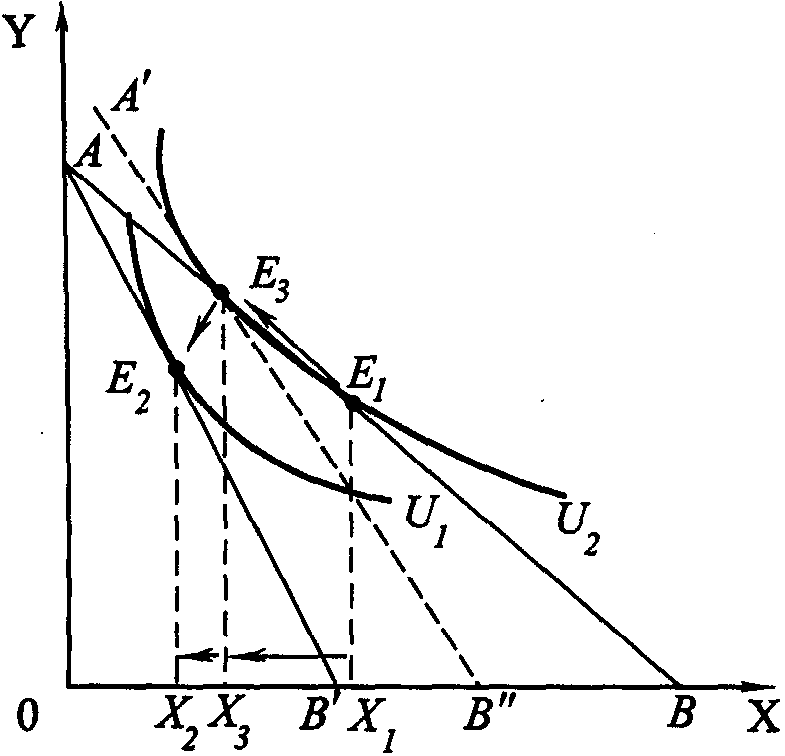
Рис. 1.14. Эффект замены и эффект дохода по Хиксу. Цена товара Х повышается
Если, напротив, цена товара Х не снижается, а повышается, то определение эффекта замены и эффекта дохода осуществляется в обратной последовательности (рис. 1.14). Здесь вспомогательная бюджетная линия А'В" касается в точке E3 кривой безразличия U2, а не U1 как это было в предыдущем примере (см. рис. 1.13).
На рис. 1.14 эффект замены представлен отрезком Х3Х1 а эффект дохода – отрезком Х2Х3.
Подход Б. Слуцкого к разделению общего эффекта изменения цены на эффект замены и эффект дохода существенно отличается от подхода Хикса. Слуцкий предложил проводить вспомогательную бюджетную линию А'В" (рис. 1.15) не как касательную к первоначальной кривой безразличия U2, а как линию, проходящую через первоначальную точку оптимума потребителя E1 и в то же время параллельную бюджетной линии АВ'. В результате такого построения вспомогательной бюджетной линии А'В" она окажется касательной для более высокой кривой безразличия U3. Точка касания E3 характеризует некий вспомогательный оптимум потребителя, которому соответствует новое соотношение цен, сложившееся в результате повышения цены на товар X.

Рис. 1.15. Эффект замены и эффект дохода по Слуцкому. Цена товара Х повышается
Поскольку все три оптимума (Е1, Е2 и E3) лежат на разных кривых безразличия (соответственно на U2, U1 и U3), то, естественно, ни о каком эффекте замены в данной ситуации не может быть и речи. Этот эффект, как известно, возникает лишь при перемещении потребителя в рамках одной и той же кривой безразличия. Данное обстоятельство позволяет сделать вывод о том, что на рис. 1.15 мы по существу имеем дело лишь с двумя эффектами дохода. Так что подход Слуцкого не позволяет решить поставленную задачу.
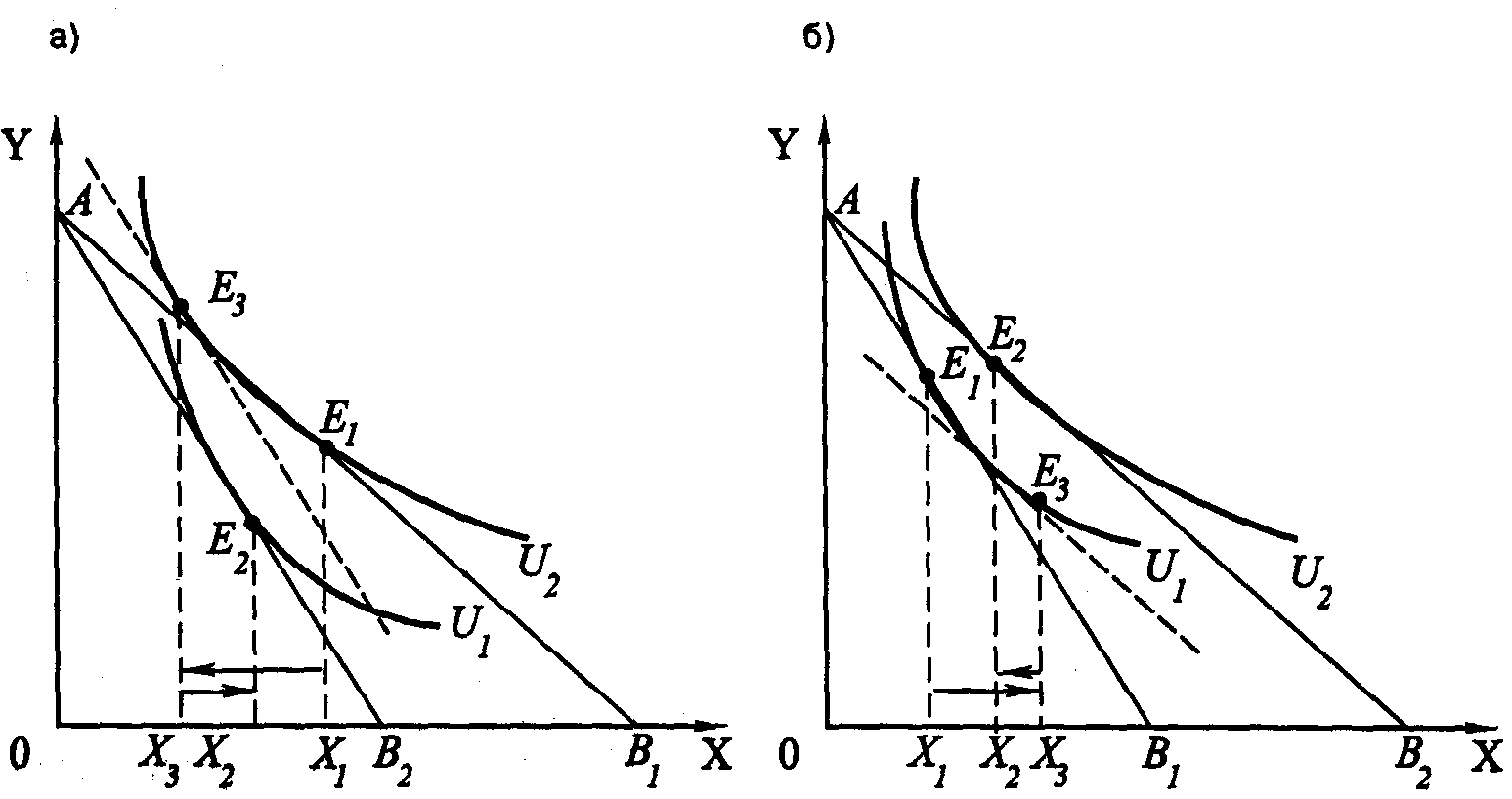
Рис. 1.16. Эффект замены и эффект дохода, когда благо Х некачественное (а – цена повышается; б – цена снижается)
1.3.2.2. Эффекты замены и дохода для некачественных товаров
До сих пор рассмотрение как общего эффекта изменения цены, так и составляющих его эффектов (замены и дохода) велось применительно к ситуации, когда оба блага качественные. В таком случае, как мы видели, эффект дохода (положительный – при снижении цены и отрицательный – при росте цены) всегда дополняет эффект замены. Если же, скажем, благо Х оказывается некачественным, то в этом случае эффект дохода (положительный – при росте цены и отрицательный – при снижении цены) становится антиподом эффекта замены (рис. 1.16).
Общий эффект изменения цены блага Х измеряется отрезком X1X2, эффект замены – отрезком Х1Х3, а эффект дохода – отрезком Х3Х2. При превышении эффектом дохода эффекта замены произойдет нарушение закона спроса. Это значит, что с повышением цены блага спрос на него будет расти, а с понижением цены – падать. Такое отступление от закона спроса называется «парадоксом Гиффена».
1.4. РЕАКЦИЯ ПОТРЕБИТЕЛЯ НА ИЗМЕНЕНИЕ ДОХОДА
1.4.1. КРИВАЯ «ДОХОД-ПОТРЕБЛЕНИЕ» ДЛЯ КАЧЕСТВЕННЫХ И НЕКАЧЕСТВЕННЫХ ТОВАРОВ
Реакция потребителя на изменение цен была рассмотрена выше. Проанализируем теперь реакцию потребителя на изменение его дохода при условии, что его предпочтения и цены благ остаются стабильными. Предположим, что исходное положение индивидуума характеризуется точкой E1 – точкой его оптимума (рис. 1.17). В ней бюджетная линия A1B1 касается кривой безразличия U1. Увеличение дохода приведет к смещению бюджетной линии в положение A2B2, что позволит индивидууму выйти на более удаленную от начала координат кривую безразличия U2. Набор, соответствующий новому оптимуму потребителя (E2), предпочтительнее набора Е1 поскольку он содержит большее количество обоих благ (X и Y). Если все полученные таким путем точки оптимума соединить одной линией, получим кривую «доход–потребление» СС. Как конфигурация, так и угол наклона этой линии могут быть разными.
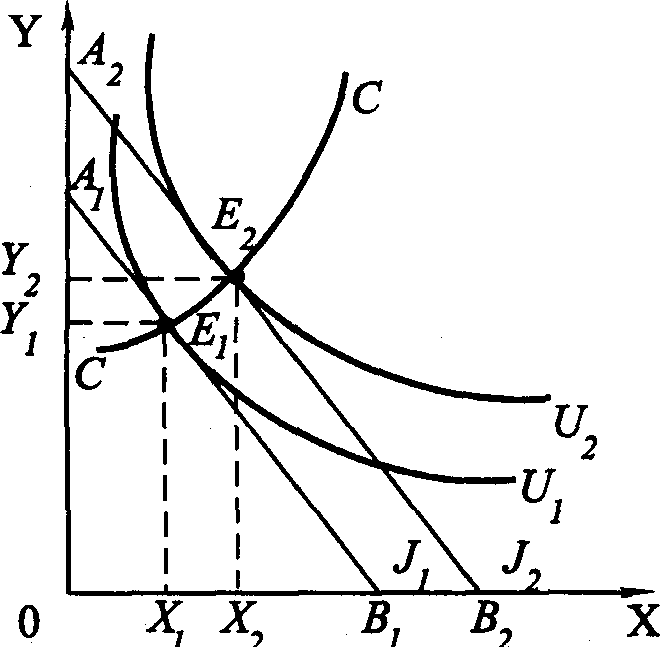
Рис. 1.17. Линия «доход-потребление» для нормальных товаров
Кривая «доход–потребление» СС, представленная на рис. 1.17, имеет положительный наклон. Это значит, что с ростом дохода спрос на оба блага увеличивается. Такие блага обычно называют нормальными или качественными. В ряде случаев кривая «доход–потребление» может иметь отрицательный наклон. Две такие ситуации представлены на рис. 1.18.
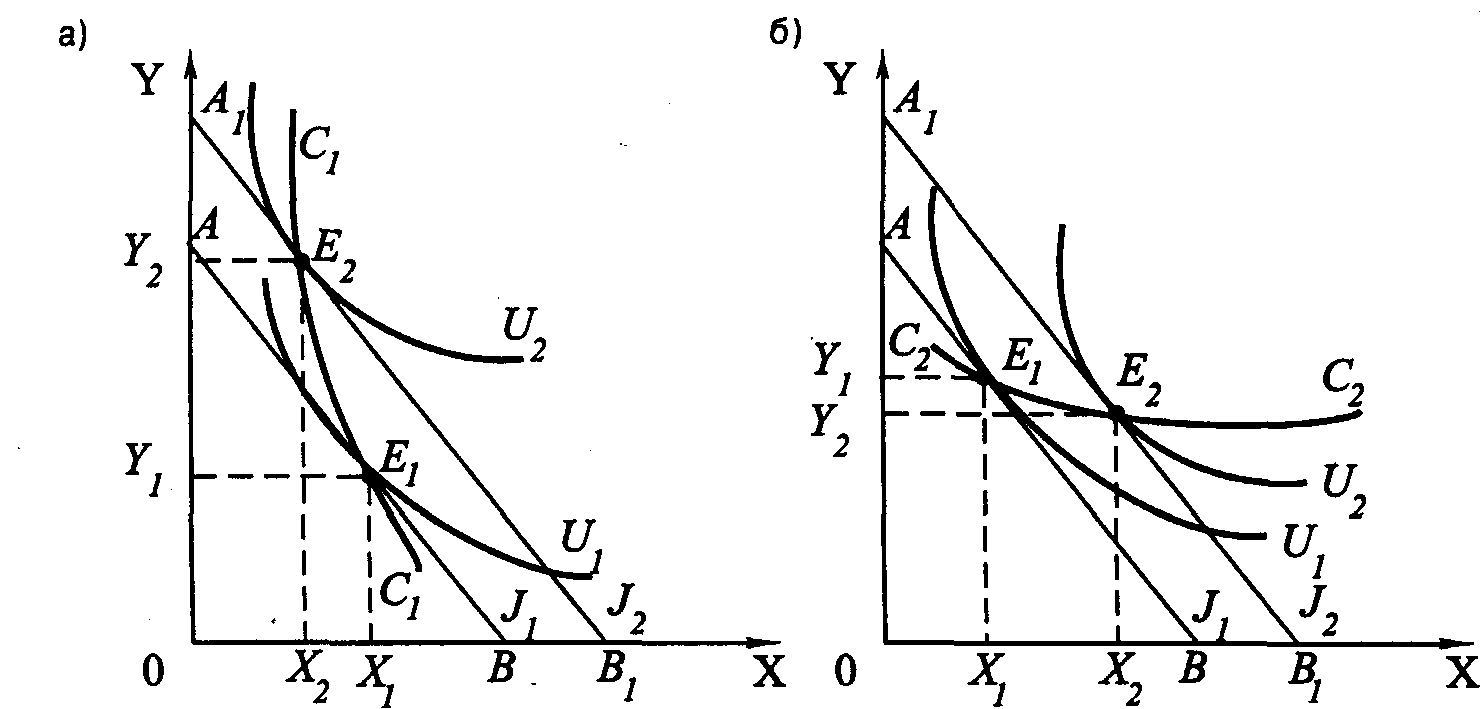
Рис. 1.18. Линия «доход-потребление», когда одно благо качественное, а другое – некачественное
Отрицательный наклон линии «доход-потребление» свидетельствует о том, что с ростом дохода индивидуума его спрос возрастает лишь на одно благо, тогда как на другое падает. Благо, спрос на которое снижается при увеличении дохода потребителя, называется некачественным. На рис. 1.18, а некачественным является благо X, а на рис. 1.18,б – благо Y.
1.4.2. КРИВЫЕ ЭНГЕЛЯ
От кривой «доход–потребление» можно легко перейти к индивидуальной кривой Энгеля, которая выражает зависимость объема потребления конкретного блага индивидуумом от величины его дохода при условии неизменности цен и предпочтений. Так, при построении кривой Энгеля для блага Х необходимо на оси абсцисс отложить изменяющийся доход индивидуума (J), а на оси ординат – оптимальные объемы потребления данного блага, выявленные в процессе нахождения кривой «доход–потребление».
Кривая Энгеля может иметь как положительный, так и отрицательный наклон. Положительный – когда благо качественное и отрицательный – когда благо некачественное.
На рис. 1.19 представлены две кривые Энгеля для блага Х (АА и A1A1). Первая из них (АА) построена на основе линии «доход–потребление» СС, изображенной на рис. 1.17, а вторая (A1A1) – на основе линии «доход–потребление» С1С1 представленной на рис. 1.18.
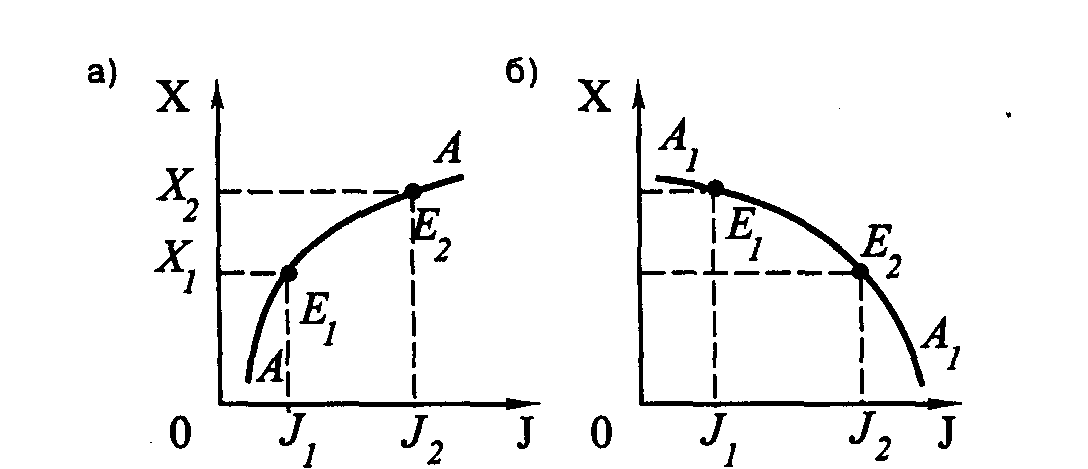
Рис. 1.19. Кривые Энгеля: а) АА – для качественного блага;
б) А1А1 – для некачественного блага
Кривые Энгеля могут быть построены также применительно не к отдельным благам, а к определенным группам благ (к продуктам питания, одежде, услугам и т. д.), объем потребления которых измерен в денежной форме, в виде расходов индивидуума. Такие кривые называются обычно кривыми расходов Энгеля. Они показывают зависимость расходов индивидуума на ту или иную группу благ от уровня его дохода. При этом предельный уровень всех расходов фиксируется с помощью луча, проведенного из начала координат под углом 45° (рис. 1.20).

Рис. 1.20. Кривая расходов Энгеля на агрегированную группу благ
Если бы случилось так, что индивидуум стал тратить весь свой доход на покупку лишь какой-то одной агрегированной группы благ (например, продуктов питания), то в этом случае кривая расходов Энгеля совпала бы с указанным лучом.
Э. Энгель (1821-1896 гг.), исследуя расходы семей с разным уровнем достатка, установил, что с ростом дохода доля его, направляемая на продукты питания, снижается, доля, расходуемая на одежду и жилье, остается в принципе неизменной, а доля, направляемая на другие нужды, увеличивается.
|
 Скачать 5.7 Mb.
Скачать 5.7 Mb.