Цены и ценообразование - Есипова В.Е.. Учебник для вузов Издание третье, исправленное и дополненное под редакцией

• Название: Учебник для вузов Издание третье, исправленное и дополненное под редакцией
• Анкор: Цены и ценообразование - Есипова В.Е..doc
• Дата: 03.02.2017
• Размер: 5.7 Mb.
• Имя файла: Цены и ценообразование - Есипова В.Е..doc
• Тип: Учебник; #1903
• Категория: Экономика. Финансы
• страница: 7 из 41

Глава 4. ПРОИЗВОДСТВО И ПРЕДЛОЖЕНИЕ БЛАГ

Понятие «производство» в обыденном сознании ассоциируется обычно с процессом изготовления, создания определенных осязаемых, или материальных, благ. Однако в экономической науке оно имеет более широкое, универсальное содержание. Экономисты называют производством любую деятельность по использованию естественных ресурсов, включая ресурсы самого человека, для получения как осязаемых, так и неосязаемых (нематериальных) благ.

Экономист включит в производство, скажем, картофеля не только его выращивание и уборку, но и перемещение его в пространстве (транспортировка) или во времени (хранение). Аналогичным образом он определит как производство оказание самых разнообразных услуг (медицинских, образовательных, консалтинговых и т. п.).

Правда, между производством хлеба и зрелищ, знаний и правосудия, информации и энергии так много «технологических» различий, что предложить единую теорию производства до сих пор не удалось и вряд ли удастся в будущем. Поэтому, а также в силу ряда исторических причин, роль такой общей теории выполняет теория материального производства, понимаемого как процесс превращения (трансформации) производственных ресурсов в выпуск (продукт).

Теория производства изучает, прежде всего, соотношение между количеством применяемых ресурсов и объемом выпуска. Методологически теория производства во многом симметрична теории потребления, с тем, однако, отличием, что основные ее категории имеют объективную природу и могут быть измерены в определенных единицах меры.

4.1. ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ И ЕЕ СВОЙСТВА

Производственная функция характеризует максимально возможный объем производства, который может быть получен при использовании данной комбинации ресурсов.

В теории производства традиционно используется двухфакторная производственная функция вида Q = f(L, К), характеризующая зависимость между объемом выпуска (Q) и количествами применяемых ресурсов труда (L) и капитала (К). Это объясняется не только удобством графического отображения, но и тем, что удельный расход материалов во многих случаях мало зависит от объема выпуска, а такой фактор, как производственная площадь, обычно рассматривается вместе с капиталом.

Производственная функция строится для данной технологии. Совершенствование технологии, увеличивающее максимально достижимый объем выпускаемой продукции при любой комбинации факторов, отражается новой производственной функцией.

Хотя производственные функции различны для разных видов производств, тем не менее, обладают и общими свойствами.

Существует предел для увеличения объема производства, который может быть достигнут увеличением затрат одного ресурса при прочих равных условиях.

Это предполагает, например, что на предприятии при данном количестве станков и производственных помещений существует предел для увеличения производства путем привлечения большего количества рабочих.

Прирост производства, который может быть достигнут при увеличении числа рабочих, занятых в нем, очевидно, будет приближаться к нулю. Действительно, можно достигнуть такой точки, когда каждый новый рабочий на предприятии будет способствовать скорее сокращению, а не увеличению выпуска продукции. Это может произойти, если рабочий не будет обеспечен оборудованием для работы и его присутствие будет мешать работе других рабочих и снижать эффективность их труда.

Существует определенная взаимная дополняемость факторов производства, кроме того, без сокращения объема производства возможна и определенная взаимозаменяемость этих факторов.

Работники выполняют свою работу более эффективно, если они снабжены всеми необходимыми инструментами. Точно так же инструменты могут оказаться бесполезными, если работники не будут обладать необходимой для их применения квалификацией.

4.1.1.ИЗОКВАНТА

Изокванта (линия равного выпуска) – кривая, представляющая бесконечное множество комбинаций факторов производства (ресурсов), обеспечивающих одинаковый выпуск продукции.

Изокванты для процесса производства означают то же, что и кривые безразличия для процесса потребления и обладают аналогичными свойствами: имеют отрицательный наклон, выпуклы относительно начала координат, не пересекаются друг с другом. Чем дальше от начала координат расположена изокванта, тем больший объем выпуска она представляет. При этом, в отличие от кривых безразличия, где суммарное удовлетворение потребителя точно измерить нельзя, изокванты показывают реальные уровни производства: 100 шт., 300 тыс. шт. и т.п.

Изокванты (как и кривые безразличия) могут иметь различную конфигурацию (рис. 4.1).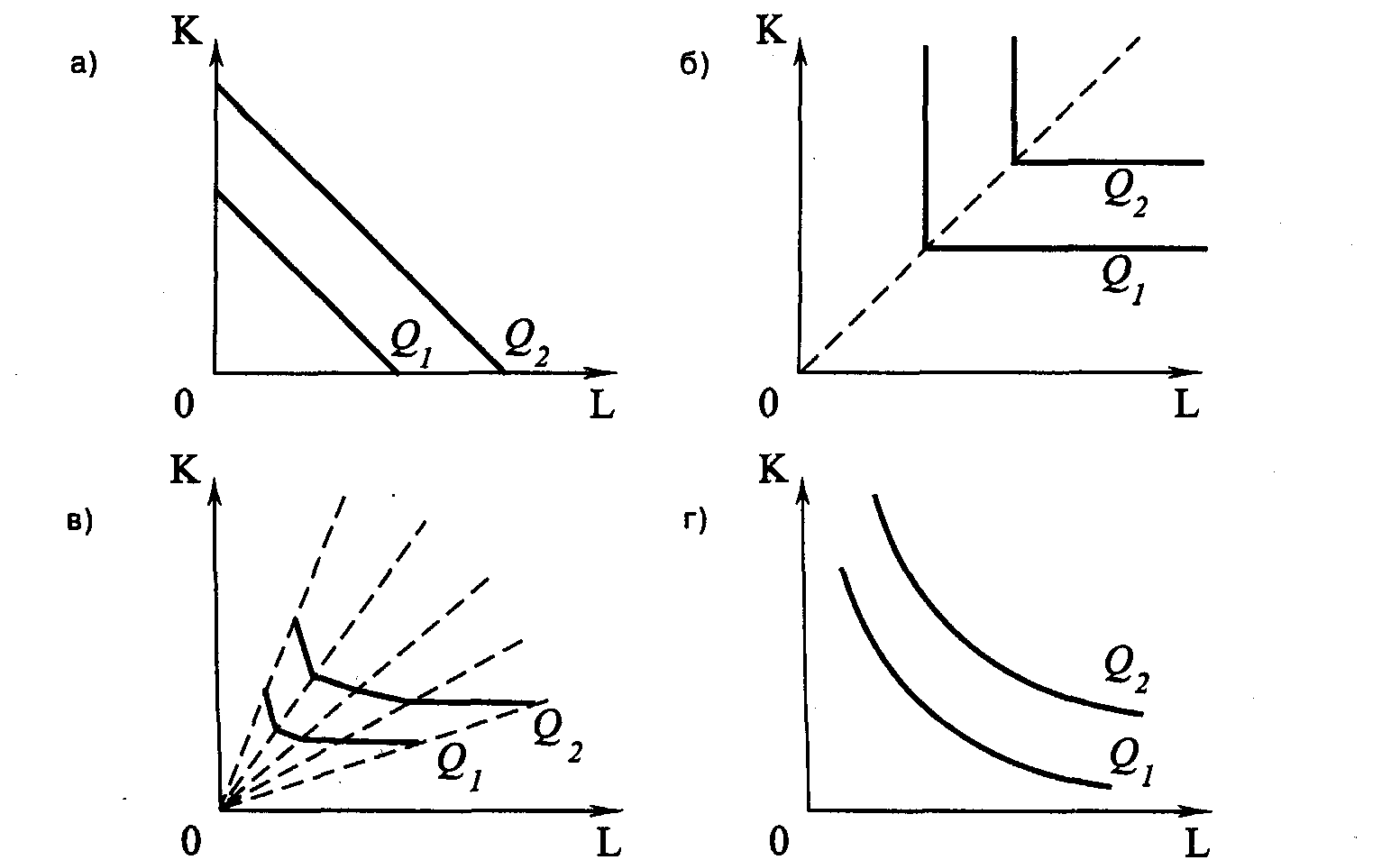


Рис. 4.1. Возможные конфигурации изокванты

Линейная изокванта (рис. 4.1, а) предполагает совершенную замещаемость производственных ресурсов, так что данный выпуск продукции может быть получен с помощью либо труда, либо только капитала, либо с использованием бесконечно возможных комбинаций того и другого ресурса. Изокванта, представленная на рис. 4.1, б, характерна для случая жесткой дополняемости ресурсов: известен лишь один метод производства данного продукта, труд и капитал комбинируются в единственно возможном соотношении.

На рис. 4.1, в показана ломаная изокванта, предполагающая ограниченную возможность замещения ресурсов (лишь в точках излома) и наличие лишь нескольких методов производства. Наконец, на рис. 4.1, г представлена изокванта, предполагающая возможность непрерывной замещаемости ресурсов в определенных границах, за пределами которых замещение одного фактора другим, технически невозможно.

Многие инженеры, предприниматели, производственники считают ломаную изокванту наиболее реалистично представляющей производственные возможности большинства современных производств. Однако традиционная экономическая теория обычно оперирует гладкими изоквантами, подобными изображенной на рис. 4.1, г, поскольку их анализ не требует применения сложных математических методов. Кроме того, изокванты такого вида можно рассматривать как некую приближенную аппроксимацию ломаной изокванты. Увеличивая число методов производства и увеличивая таким образом число точек излома, мы можем (в пределе) представить ломаную изокванту в виде гладкой кривой.

4.1.2. ВЗАИМОЗАМЕНЯЕМОСТЬ ФАКТОРОВ ПРОИЗВОДСТВА

Наклон изоквант характеризует предельную норму технического замещения одного фактора другим:

. (4.1)

Предельная норма технического замещения капитала трудом представляет собой величину, на которую может быть сокращен капитал за счет использования одной дополнительной единицы труда при фиксированном объеме выпуска продукции (Q = const).

4.2. ПРОИЗВОДСТВО И ВРЕМЕННОЙ ГОРИЗОНТ ФИРМЫ

Возможности изменить используемые в производстве объемы труда и капитала неодинаковы. Если спрос на продукцию фирмы возрастает, то на первых порах увеличение производства достигается за счет дополнительного привлечения труда на те же производственные мощности, поскольку для расширения последних, как правило, требуется больше времени. В связи с этим вводятся понятия: мгновенный, короткий и длительный период.

4.2.1. МГНОВЕННЫЙ, КОРОТКИЙ И ДЛИТЕЛЬНЫЙ ПЕРИОД

Мгновенный период – период производства, в течение которого все факторы производства постоянны.

Короткий период – период производства, в течение которого некоторые производственные ресурсы не могут быть изменены (например, промышленные фирмы ограничены имеющимися у них производственными мощностями).

Длительный период – период времени, в течение которого производители могут изменить все факторы производства, используемые для изготовления продукта.

Типичной формой производственной функции длительного периода является степенная функция вида:

(4.2)

где А, α и β– положительные постоянные числа, характеризующие технологию производства. Статистика обычно определяет эти коэффициенты для отдельных отраслей. Каждый из показателей степени меньше единицы. Производственная функция, у которой α + β= 1, называется производственной функцией Кобба–Дугласа.
4.2.2. СОВОКУПНЫЙ, ПРЕДЕЛЬНЫЙ И СРЕДНИЙ ПРОДУКТ В КРАТКОСРОЧНОМ ПЕРИОДЕ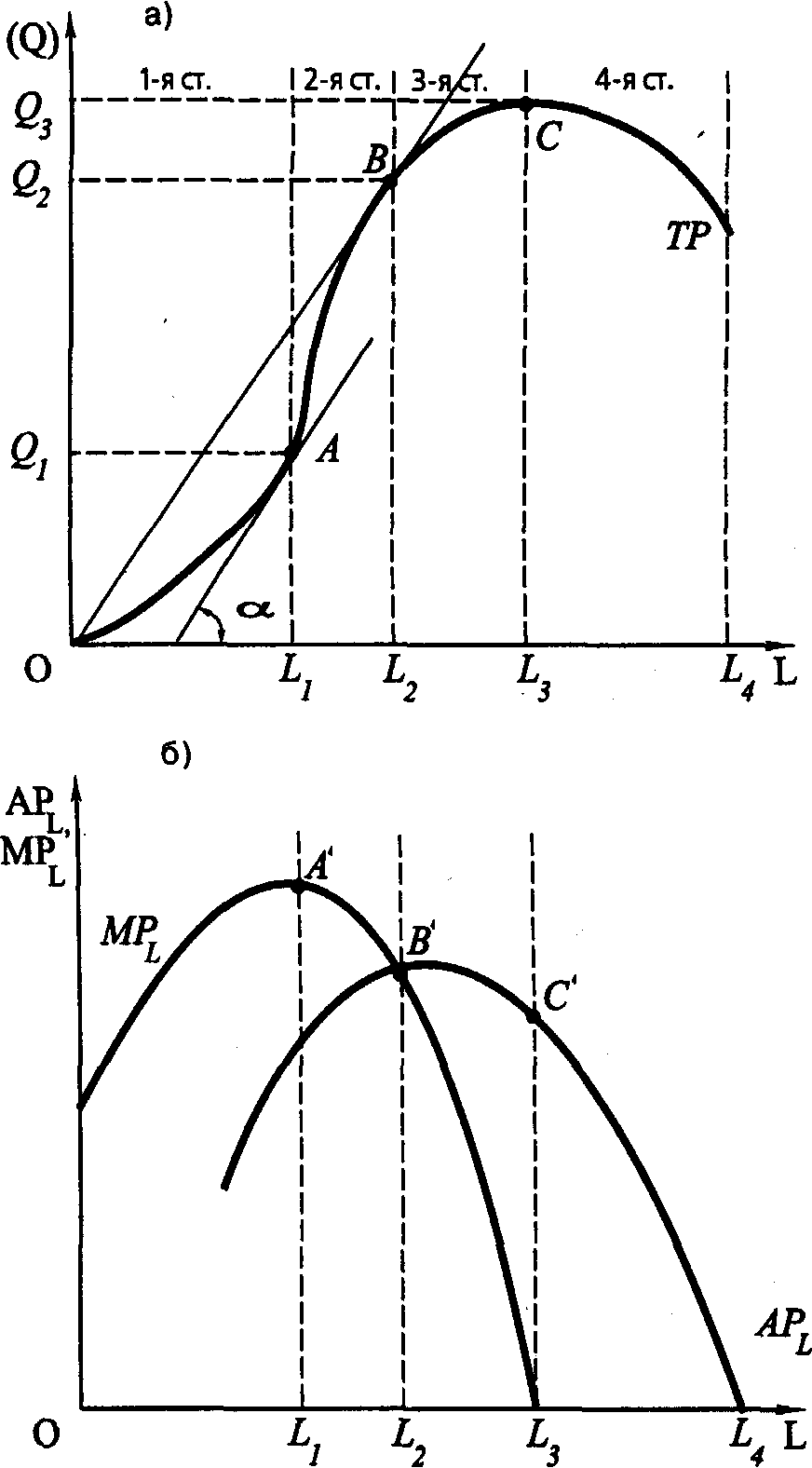



Рис.4.2. Совокупный, средний и предельный продукт

Совокупный (общий) продукт – это количество блага, произведенное с использованием некоторого количества переменного ресурса при фиксированном количестве постоянного ресурса (ТР = Q).

Разделив совокупный продукт на израсходованное количество переменного фактора, можно получить средний продукт:

(4.3)

Предельный продукт – прирост общего продукта, полученного в результате увеличения использования данного ресурса на единицу:

(4.4)

Графически величина предельного продукта определяется тангенсом угла наклона касательной к кривой общего продукта в точке, соответствующей определенному его объему. На рис. 4.2 представлены кривые совокупного, среднего и предельного продукта переменного ресурса L.
4.2.3. ЗАКОН УБЫВАЮЩЕЙ ПРЕДЕЛЬНОЙ ПРОИЗВОДИТЕЛЬНОСТИ

Совокупный продукт с ростом использования в производстве переменного фактора (в данном случае L) будет увеличиваться, однако этот рост имеет определенные пределы в рамках заданной технологии. На первой стадии производства ОА (рис. 4.2, а) увеличение затрат труда способствует все более полному использованию капитала: предельная и общая производительность труда растут. Это выражается в росте предельного и среднего продукта, при этом МР > АР. В точке А' (рис. 4.2, б) предельный продукт достигает своего максимума. На второй стадии АВ (рис. 4.2, а) величина предельного продукта уменьшается и в точке В' (рис. 4.2, б) становится равной среднему продукту МР = АР. На третьей стадии производства (ВС) МР < АР, в результате чего совокупный продукт растет медленнее затрат переменного фактора. На четвертой стадии МР < 0 прирост переменного фактора приводит к уменьшению выпуска совокупной продукции. В этом и заключается закон убывающей предельной производительности. Он гласит, что при увеличении использования переменного ресурса, в то время как другие ресурсы и технология неизменны, предельный продукт этого ресурса будет снижаться.

Рациональный предприниматель не будет увеличивать объем применения переменного ресурса L свыше уровня L₃, поскольку это приведет к сокращению величины ТР.

В деловой жизни способность распознавать технологические пределы имеет решающее значение при определении успеха или неудачи компании. Эти пределы – самый надежный ключ к выявлению момента, когда данная технология, машина, процесс устаревают.

Закон убывающей предельной производительности применим к определенной технологии производства и на краткосрочном отрезке времени. Со временем изобретения и другие технологические новшества могут привести к подъему всей кривой выпуска продукции, и, таким образом, больший выпуск может быть достигнут при тех же самых вводимых факторах.

4.3. РАСШИРЕНИЕ ПРОИЗВОДСТВА

Расширение производства возможно различными путями. При сохранении неизменной технической базы увеличить выпуск можно за счет увеличения применения всех видов ресурсов. В этом случае имеет место увеличение масштабов производства, для его анализа используется понятие отдача от масштаба. В коротком периоде можно увеличить объем применения лишь переменного ресурса. В этом случае имеет место изменение пропорций, в которых применяются производственные ресурсы. Расширение производства в коротком периоде исследуется с помощью понятия убывающей отдачи (или убывающей производительности) переменного ресурса или, как иногда говорят, закона изменяющихся пропорций. Возможно также расширение производства за счет изменения его технической базы, то есть научно-технического прогресса.

4.3.1. ОТДАЧА ОТ МАСШТАБА

При выборе технически эффективного метода производства увеличение выпуска возможно за счет пропорционального увеличения использования всех производственных ресурсов. Это и есть изменение масштаба производства.

Пусть первоначальное соотношение между выпуском и применяемыми ресурсами описывается производственной функцией:

Q₀=f(K,L).

Если мы увеличим объемы применяемых ресурсов (масштаб производства) в k раз, то новый объем выпуска составит:

Q₁ = f(kK, kL).

В результате получим:

• 
  постоянную отдачу от масштаба, когда выпуск увеличится также в k paз (Q₁=kQ₀);
  
• 
  убывающую отдачу от масштаба, если выпуск увеличится менее чем в k paз(Q₁ < kQ₀);
  

• 
  в возрастающую отдачу от масштаба при увеличении выпуска более чем в k раз (Q₁ > kQ₀).
  

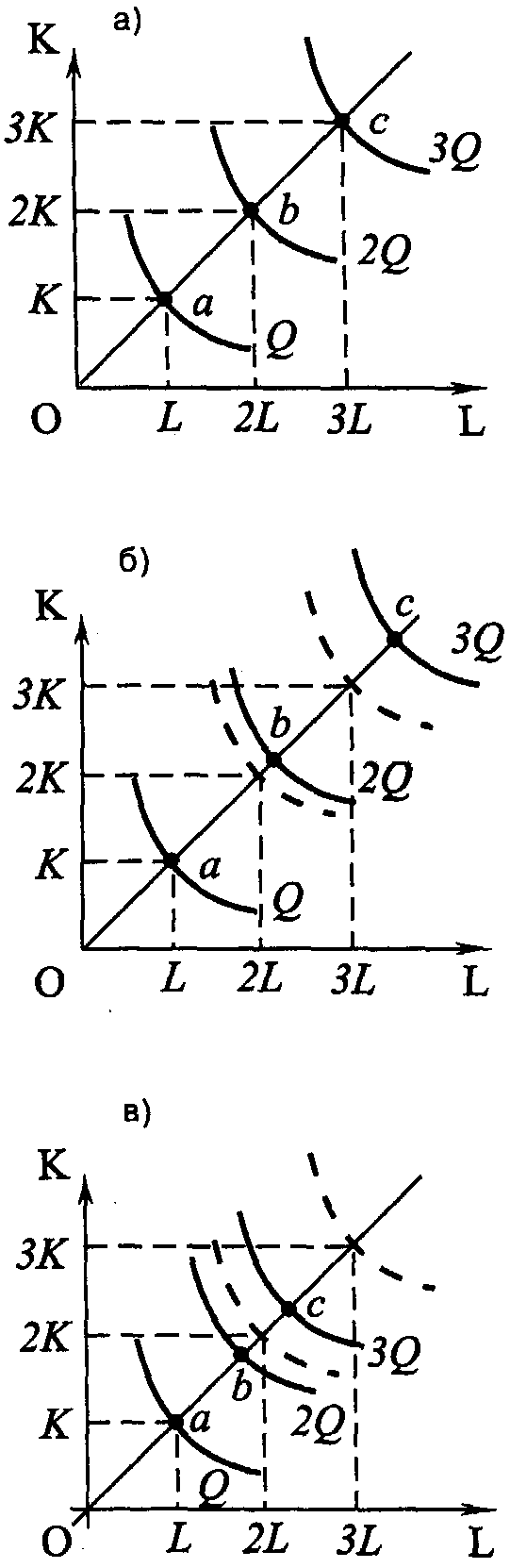Рис. 4.3. Отдача от масштаба

Введем еще одну характеристику производственной функции – однородность. Производственная функция называется однородной, если при увеличении количества всех производственных ресурсов в k раз выпуск увеличивается в k^t раз, так что

Q₁=(kK, kL) = k^tQ₀(K, L) (4.5)

Показатель t характеризует степень однородности функции. Если же равенство (4.5) для данной производственной функции не выполняется, то такая производственная функция называется неоднородной.

Степень однородности может использоваться для характеристики типа отдачи от масштаба, если:

• t = 1 – отдача от масштаба постоянна;

• t < 1 – убывающая отдача от масштаба;

• t > 1 – возрастающая отдача от масштаба.

Для однородной производственной функции отдача от масштаба может быть представлена графически. Показателем отдачи служит расстояние вдоль луча, проведенного из начала координат между изоквантами, представляющими кратные Q объемы выпуска – Q, 2Q, 3Q и т. д. (рис. 4.3). В случае неоднородности производственной функции оценка отдачи от масштаба и ее графическое отображение сопряжены со значительными трудностями.

Постоянная отдача от масштаба наблюдается в тех производствах, где ресурсы однородны (в техническом смысле) и их количества можно изменять пропорционально. В таких производствах увеличение выпуска может быть достигнуто путем кратного увеличения объема применения всех производственных ресурсов. Убывающая отдача, как правило, связана с ограниченными возможностями управления крупным производством. Концентрация управления (на неизменной технической базе) сверх определенного предела ведет к нарушению координации потоков ресурсы–выпуск.

Во многих случаях характер отдачи от масштаба изменяется при достижении определенных пределов выпуска. До определенных пределов рост производства сопровождается постоянной и даже возрастающей отдачей от масштаба, которая затем сменяется убывающей.

Лучи, проведенные из начала координат на рис. 4.3, называют линиями роста. Они характеризуют технически возможные пути расширения производства, то есть переход с более низкой на более высокую изокванту.

Среди возможных линий роста представляют интерес изоклинали, вдоль которых предельная норма технического замещения ресурсов при любом объеме выпуска постоянна.

4.3.2. УБЫВАЮЩАЯ ОТДАЧА ПЕРЕМЕННОГО РЕСУРСА

(ЗАКОН ИЗМЕНЯЮЩИХСЯ ПРОПОРЦИЙ)

В коротком периоде, в отличие от длительного, часть ресурсов остается неизменной, тогда как другая часть может быть увеличена. Поэтому для короткого периода линия роста представлена не лучом, проведенным из начала координат, а прямой, параллельной оси переменного фактора. Очевидно, что соотношение K/L вдоль такой линии уменьшается, поскольку фиксированное количество К приходится на все большее количество L. Таким образом, в коротком периоде рост выпуска происходит при изменяющихся пропорциях между постоянным и переменным ресурсом.

При этом увеличение количества переменного ресурса рано или поздно приведет к сокращению предельного и среднего продукта этого ресурса. Очевидность такого утверждения следует хотя бы из простого примера. Возможно ли, увеличивая количество удобрений, достигнуть такой урожайности, что весь мировой урожай мог бы собираться на участке земли, не превышающем по площади размеров цветочной клумбы?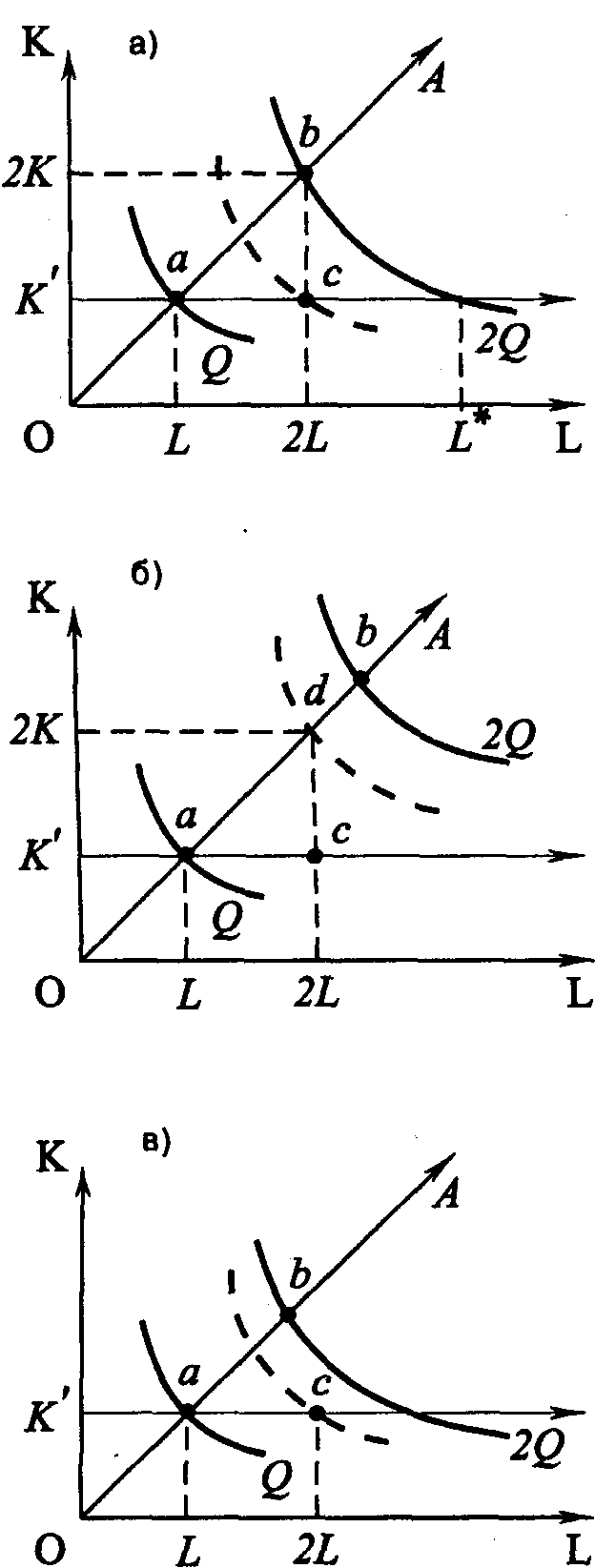



Рис. 4.4. Убывающая отдача переменного ресурса

(закон изменяющихся пропорций)

Действие закона изменяющихся пропорций иллюстрирует рис.4.4.

При постоянной отдаче от масштаба, как мы знаем, удвоение обоих факторов ведет и к удвоению объема выпуска. На рис. 4.4, а точка b на изоклинали ОА лежит на изокванте, соответствующей удвоенному выпуску 2Q. Если же постоянный ресурс будет зафиксирован в объеме К', а объем переменного ресурса L будет вдвое больше, мы достигнем лишь точки С, лежащей на более низкой изокванте, чем 2Q. Для достижения же выпуска 2Q нам потребуется увеличить использование переменного ресурса L до L*, то есть более чем в два раза. Следовательно, увеличение переменного ресурса при фиксированном объеме постоянного характеризуется убывающей производительностью. Очевидно, что в случае убывающей отдачи от масштаба (рис. 4.4, б) удвоение переменного ресурса дает еще меньший относительный прирост выпуска, чем при постоянной отдаче. При возрастающей отдаче от масштаба (рис. 4.4, в) производительность переменного фактора также падает.

4.3.3. ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ И ТЕХНИЧЕСКИЙ ПРОГРЕСС

Рост производства возможен наконе, за счет технического прогресса, который заключается в появлении новых, технически более эффективных способов производства. Эти новые способы должны быть учтены в производственной функции, тогда как ставшие технически неэффективными способы – исключены из нее.

Графически технический прогресс может быть отображен сдвигом вниз изокванты, характеризующей определенный объем выпуска, и, возможно, изменением ее конфигурации. На рис. 4.5 изокванта Q₁ характеризует тот же объем выпуска, что и изокванта Q₀. Но теперь этот объем может быть произведен с использованием меньших количеств ресурсов К и L.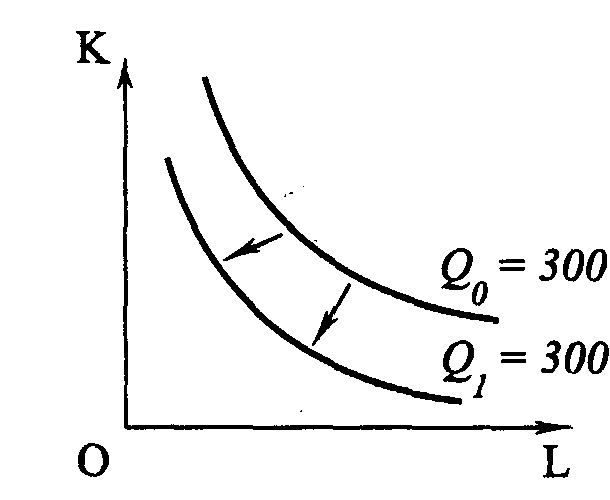


Рис. 4.5. Сдвиг изокванты в результате технического прогресса

Сдвиг изокванты может сопровождаться изменением ее конфигурации, что означает изменение и в соотношениях применяемых ресурсов. Обычно в связи с этим различают три типа технического прогресса: капиталоинтенсивный, трудоинтенсивный и нейтральный (рис. 4.6).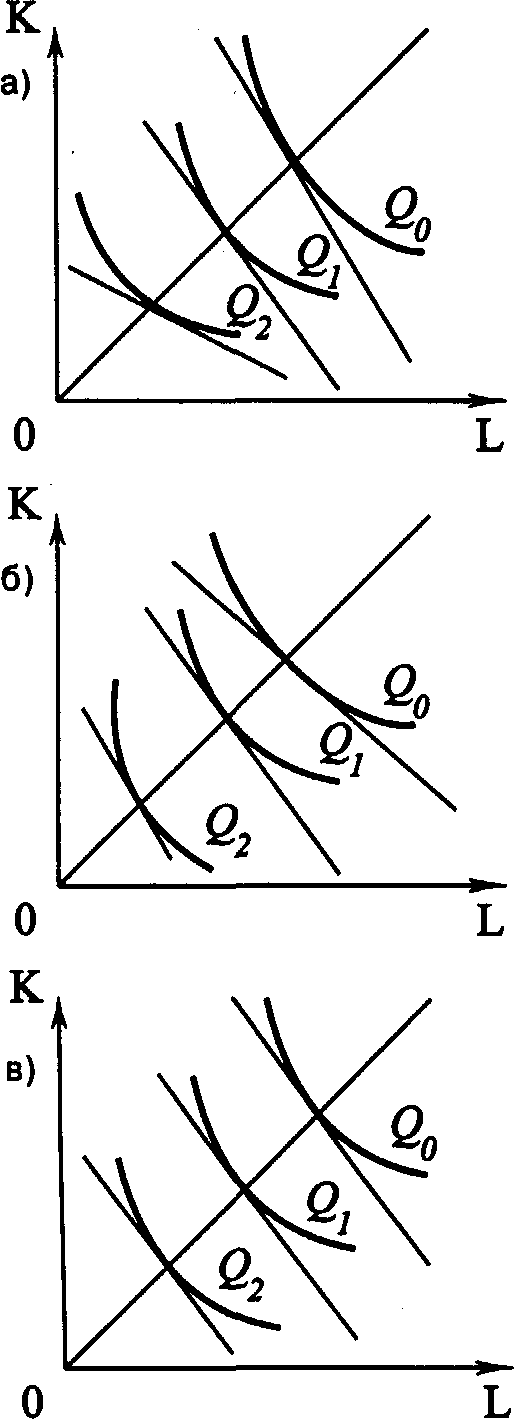



Рис.4.6. Типы технического прогресса: а) капиталоинтенсивный, б) трудоинтенсивный,

в) нейтральный.
Технический прогресс называется капиталоинтенсивным (трудосберегающим), если при движении вдоль линии с постоянным соотношением K/L предельная норма технического замещения MRTS_LK снижается (рис. 4.6, а). Это значит, что технический прогресс сопровождается опережающим увеличением предельного продукта капитала по сравнению с предельным продуктом труда. Наклон изокванты по мере приближения к началу координат становится более пологим (относительно оси L).

Технический прогресс называется трудоинтенсивным (капиталосберегающим), если при движении вдоль той же линии MRTS_LK возрастает (рис. 4.6, б). Это значит, что технический прогресс сопровождается увеличением предельного продукта труда по сравнению с предельным продуктом капитала. Наклон изокванты по мере приближения к началу координат становится более пологим (относительно оси К).

Нейтральным технический прогресс называется в том случае, если он сопровождается пропорциональным увеличением предельных продуктов К и L, так что предельная норма их технического замещения при движении к началу координат остается неизменной. Не меняется при этом и наклон изокванты, под воздействием технического прогресса она смещается параллельно себе самой (рис. 4.6, в).

4.4. ОПТИМАЛЬНАЯ КОМБИНАЦИЯ РЕСУРСОВ И ОПТИМАЛЬНЫЙ ПУТЬ РОСТА

4.4.1. РАВНОВЕСИЕ ПРОИЗВОДИТЕЛЯ

Анализ с помощью изоквант имеет для производителя очевидные недостатки, так как использует только натуральные показатели затрат ресурсов и выпуска продукции. В теории производства равновесие производителя определяется симметричным равенством предельной нормы технического замещения ресурсов К и L соотношению их цен. Если обозначить цену услуг капитала (арендную плату за час работы оборудования) через r, а цену услуг труда (часовую ставку заработной платы) через w, то условие равновесия (оптимума) производителя можно записать в виде (Q = const):

(4.6)

Роль бюджетной прямой в теории производства выполняет линия равных затрат – изокоста, представляющая множество всех комбинаций ресурсов, которые могли бы быть приобретены предприятием при определенной сумме денежных расходов. Обозначив сумму возможных расходов предприятия через С, получим бюджетное ограничение
C=r x K + w x L, (4.7)

откуда легко определить уравнение изокосты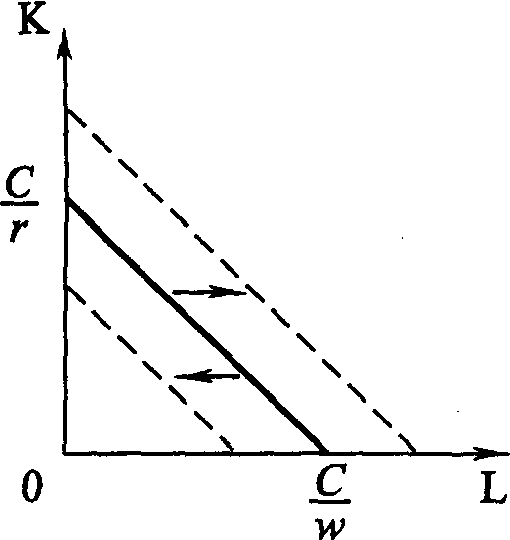

(4.8)


Рис.4.7. Изокоста
Соотношение цен факторов w/r, как очевидно, характеризует наклон изокосты. Рост бюджета производителя или пропорциональное снижение цен ресурсов сдвигает изокосту вправо, а сокращение бюджета или рост цен – влево (рис. 4.7).

Оптимальная комбинация ресурсов представлена на рис. 4.8.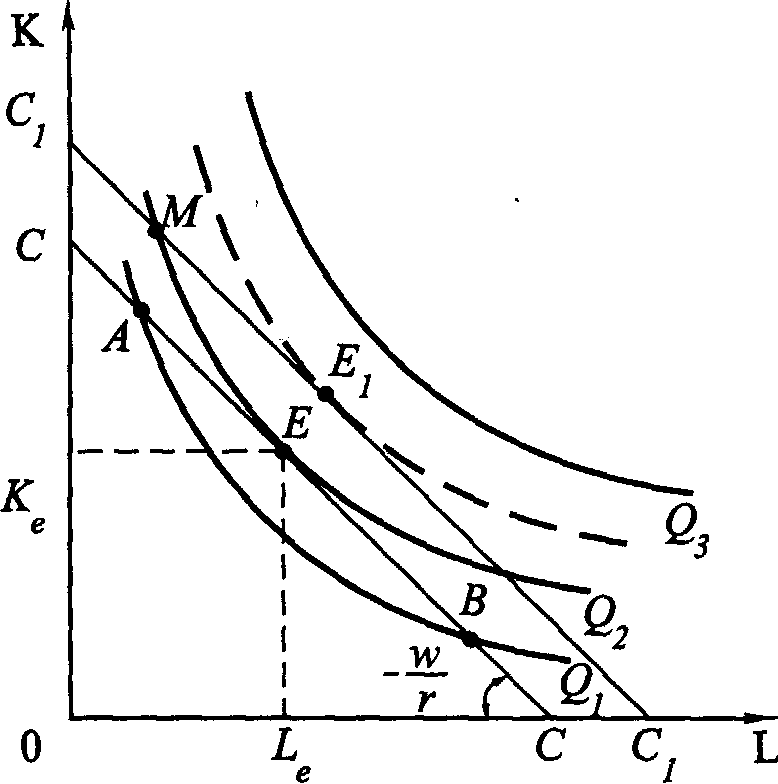



Рис. 4.8. Равновесие производителя

Комбинации ресурсов А, Е, В лежат на одной и той же изокосте СС и, значит, обойдутся при данных ценах ресурсов предприятию в одну и ту же сумму С. Но комбинация Е является наиболее предпочтительной из них, поскольку принадлежит наиболее высокой из всех достижимых при данном уровне затрат изокванте Q₂. Комбинация ресурсов Е обеспечит, таким образом, и наибольший выпуск по сравнению с любой другой комбинацией ресурсов, имеющей равную стоимость.

Комбинация ресурсов М технически столь же эффективна, как и комбинация Е. Но при данных ценах ресурсов (мы полагаем пока цены ресурсов неизменными) комбинация М экономически неэффективна. Ведь за ту же сумму средств С₁C₁ предприятие может приобрести комбинацию ресурсов Е₁ позволяющую получить больший объем продукции.

4.4.2. ОПТИМАЛЬНЫЙ ПУТЬ РОСТА

Предположим, что цены ресурсов остаются неизменными, тогда как бюджет предприятия постоянно растет. Соединив точки касания изоквант с изокостами, мы получим линию OG – «путь развития» (путь роста). Эта линия показывает темпы роста соотношения между факторами в процессе расширения производства (рис.4.9).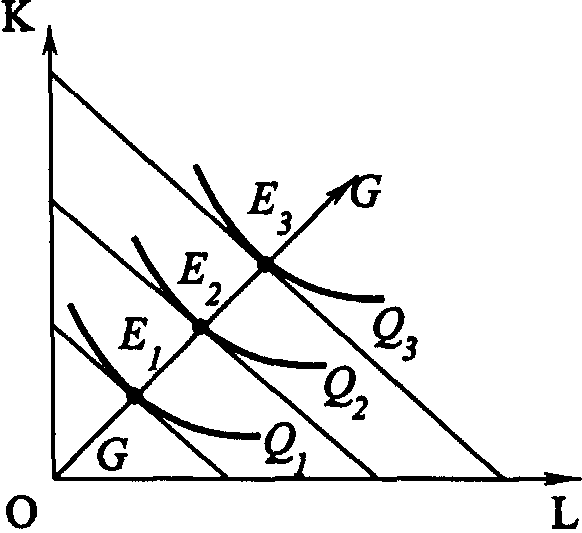


Рис. 4.9. Кривая «путь развития»

В длительном периоде все производственные ресурсы переменны, и поэтому здесь в принципе не существует предела расширению производства.

Задача предприятия в этом случае сводится к задаче выбора оптимального пути роста. При данной производственной функции и данных ценах ресурсов, оптимальный путь роста рассчитывается по множеству точек касания соответствующих изоквант и изокост. Если производственная функция однородна, оптимальный путь роста определяется лучом, выходящим из начала координат, наклон которого определяет оптимальное соотношение K/L и зависит от соотношения цен ресурсов (рис. 4.10).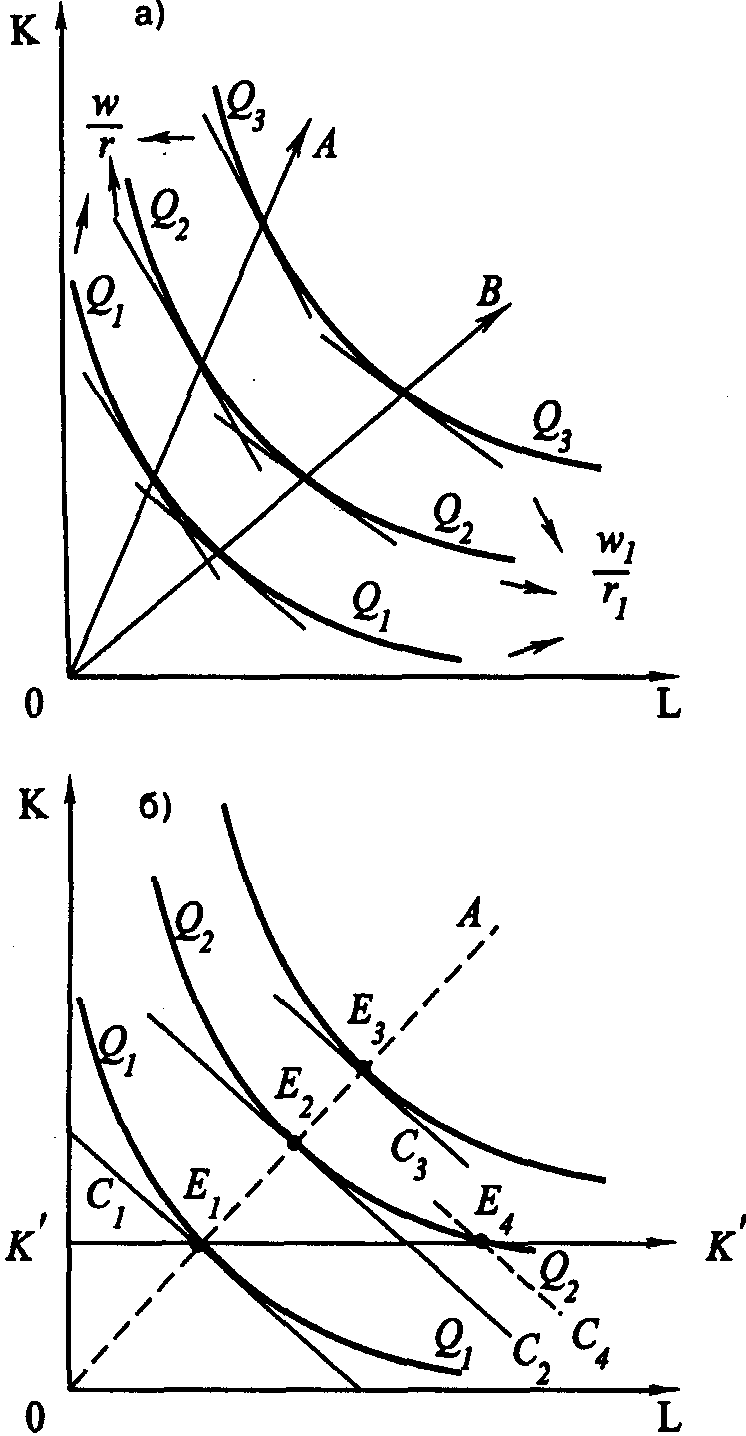



Рис. 4.10. Рост производства: а) в длительном периоде, б) в коротком периоде
На рис. 4.10, а при соотношении цен w/r оптимальный путь роста определяется лучом ОА, а при соотношении цен w₁/r₁ – лучом OВ. Понятно, что при изменении соотношения цен произойдет и изменение оптимального пути роста.

В коротком периоде (рис. 4.10., б) количество ресурса К фиксировано на уровне К' и предприятие может расширять производство лишь за счет увеличения количества переменного ресурса, то есть вдоль линии К' К', параллельной оси L. При данных ценах ресурсов их оптимальная комбинация недостижима. В самом деле, оптимальным путем роста было бы движение вдоль пунктирного луча ОА. Однако при фиксированном количестве постоянного фактора К точки E₂ и Е₃ недостижимы, а рост производства возможен лишь вдоль линии К' К'. Очевидно, что при данных ценах увеличение выпуска в коротком периоде потребует более высоких затрат (изокоста С₄ расположена дальше от начала координат, чем изокоста C₂ при том же объеме выпуска Q₂).

4.5. ИЗМЕНЕНИЕ ЦЕНЫ РЕСУРСА: ЭФФЕКТ ЗАМЕНЫ И ЭФФЕКТ ВЫПУСКА

Мы уже знаем, что изменение цены товара графически отображается поворотом бюджетной прямой по часовой стрелке или против нее. Таким же образом поворотом изокосты отображается и изменение цены производственного ресурса. Так, на рис. 4.11 линии CC₁ – СС₃ характеризуют положение изокосты при повышении цены переменного фактора L (w), GG – линия изменения цены.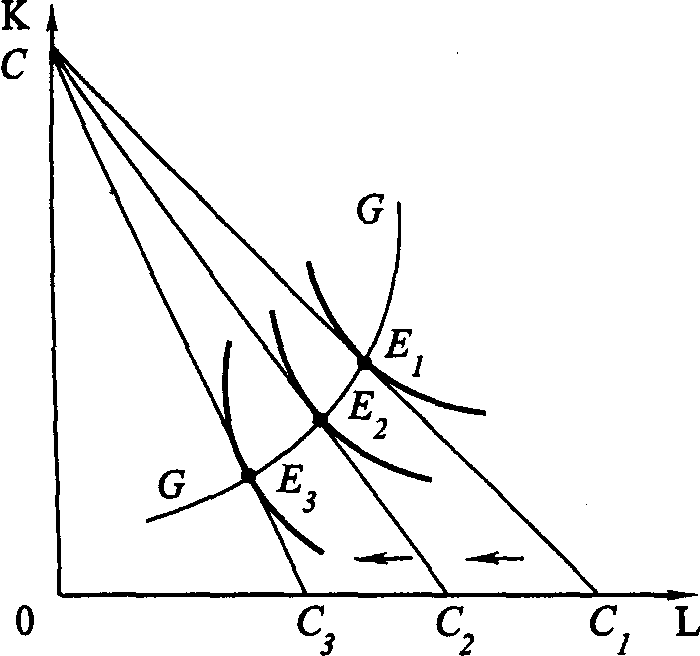



Рис. 4.11. Поворот изокосты при повышении ставки оплаты труда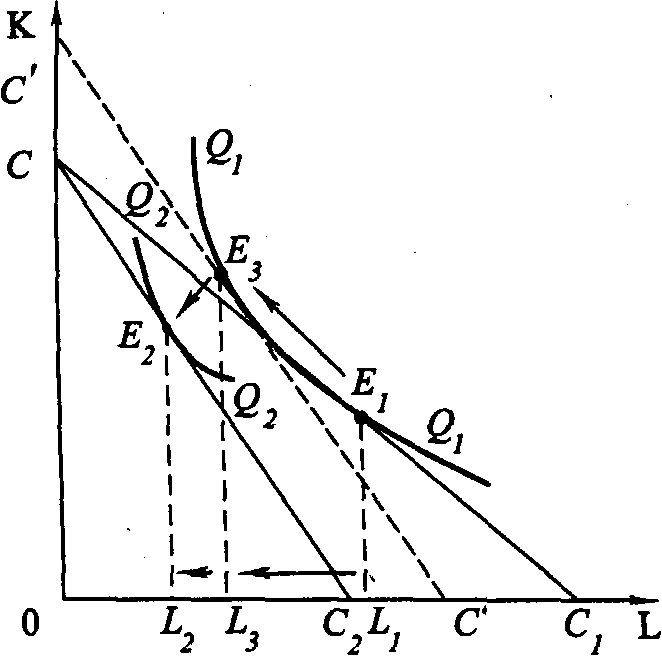


Рис. 4.12. Эффект замены и эффект выпуска (нормальный ресурс)

Общий результат изменения цены ресурса может быть разложен на две части, одна из которых представляет эффект замены, вторая – эффект выпуска.

Разложение общего результата изменения цены переменного фактора на эффект замены и эффект выпуска представлено на рис. 4.12. При цене переменного ресурса w₁ изокоста занимала положение СС₁. При повышении цены до w₂, она заняла положение CC₂. Общая сумма затрат на ресурсы не изменилась (точка С на оси ординат сохранила свое положение). В результате оптимальная комбинация ресурсов сместилась из точки E₁ в точку E₂. Общий результат повышения цены переменного ресурса выразился в сокращении объема его применения с L₁ до L₂.

Для разложения этого результата на эффект замены и эффект выпуска проведем параллельно СС₂ вспомогательную изокосту С'С' так, чтобы она касалась изокванты Q₁Q₁ (точка касания – E₃). Вдоль дуги Е₁Е₃ происходит замещение ресурсом К относительно подорожавшего переменного ресурса L при сохранении объема выпуска Q₁Q₁. Таким образом, эффект замены составил L₁ – L₃.

Однако, поскольку общая сумма затрат С остается неизменной, повышение цены переменного ресурса приводит к сокращению выпуска с Q₁ до Q₂, а точка, характеризующая оптимальную комбинацию ресурсов, смещается из E₃ в E₂. Это смещение и характеризует эффект выпуска. В единицах временного ресурса эффект выпуска составит L₃ – L₂. Таким образом, общий результат изменения цены переменного ресурса на рис. 4.12 можно разложить на эффект замены и эффект выпуска:

L₁- L₂ = (L₁-L₃) + (L₃ – L₂). (4.9)

Эффект замены всегда отрицателен, повышение цены ресурса ведет к сокращению, а ее снижение – к увеличению объема применения данного ресурса. Эффект выпуска для нормальных ресурсов также отрицателен, его действие усиливает влияние эффекта замены. Для некачественных ресурсов влияние эффекта замены и эффекта дохода разнонаправлено, а общий результат их действия непредопределен. На рис. 4.13 эффект выпуска положителен – снижение выпуска с Q₁Q₁ до Q₂Q₂ сопровождается увеличением объема применения подорожавшего переменного ресурса с L₃ до L₂. При этом эффект выпуска перекрывает эффект замены (L₁ – L₃), так что общий результат положителен.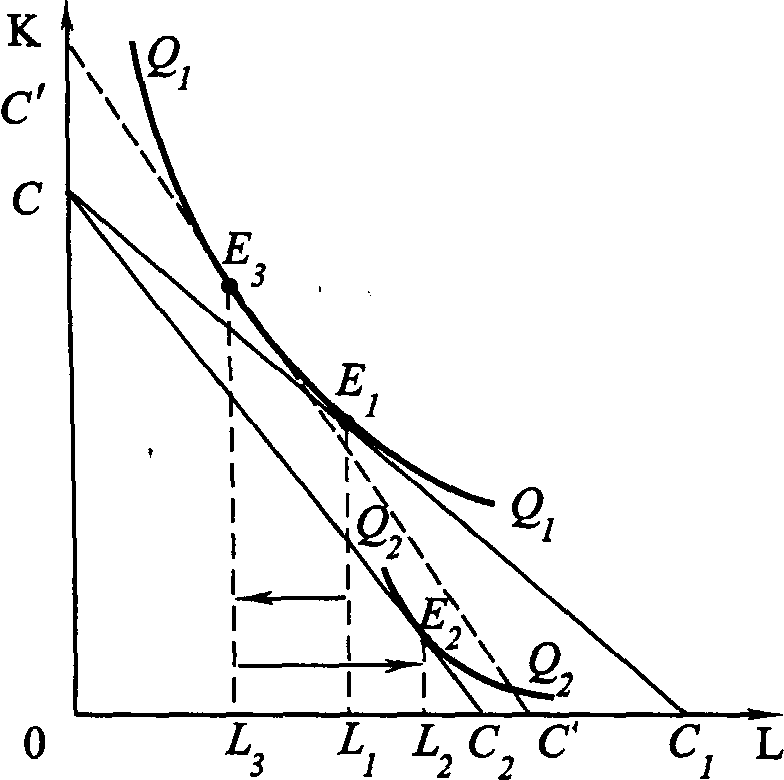


Рис. 4.13. Эффект замены и эффект выпуска (некачественный ресурс)

4.6. ФУНКЦИЯ И ЭЛАСТИЧНОСТЬ ПРЕДЛОЖЕНИЯ

4.6.1. ФУНКЦИЯ ПРЕДЛОЖЕНИЯ

Функцией предложения называют зависимость объема предложения от определяющих его факторов:

Q_SA = f(P_A,P_B,…,P_Z,R,K,C,X…)

где Q_SA – объем предложения товара А в единицу времени;

Р_A, P_B ..., Р_Z – цены данного и остальных товаров;

R – наличие производственных ресурсов;

К – характер применяемой технологии;

С – налоги и дотации;

Х – природно-климатические условия.

Зависимость между ценой блага и максимальным объемом его предложения при прочих неизменных условиях называется функцией предложения по цене: Q_S= f (P). Графически это представлено на рис. 4. 14.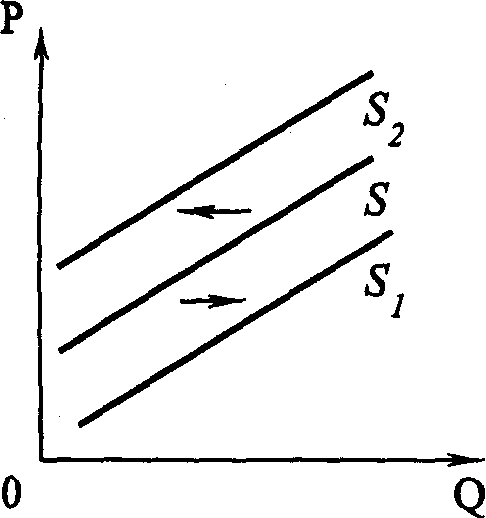



Рис. 4.14. Кривая предложения

Движение вдоль кривой предложения означает изменение объема предложения: чем выше цена, тем выше (при прочих равных условиях) объем предложения, и наоборот, чем ниже цена, тем ниже объем предложения.

Сдвиг кривой предложения влево или вправо отражает изменение предложения: оно происходит под влиянием изменения всех факторов, определяющих функцию предложения, кроме цены данного товара.

Цена предложения – минимальная цена, по которой потребитель готов предложить на рынке данное количество товара.

4.6.2. ИЗЛИШЕК ПРОИЗВОДИТЕЛЯ

Разность между суммой денег, полученной за проданную продукцию, и минимальной суммой денег, за которую производитель готов был продать эту продукцию, называется излишком производителя.

Наглядно излишек производителя представлен на рис.4.15.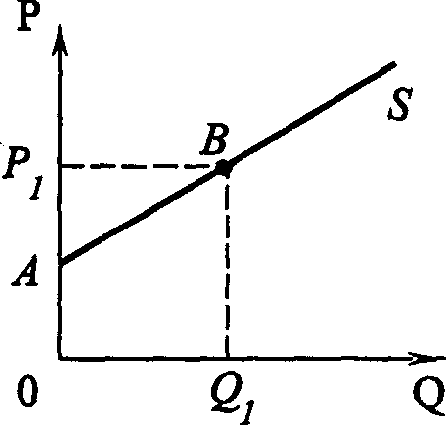



Рис. 4.15. Излишек производителя
Площадь прямоугольника Р₁ВQ₁О представляет выручку от продажи Q₁ единиц продукции, а площадь трапеции OABQ₁ соответствует минимальной сумме денег, за которую фирма могла бы продать Q₁ единиц продукции без убытков в коротком периоде. Следовательно, излишек производителя – площадь треугольника AP₁B.

4.6.3. ЭЛАСТИЧНОСТЬ ПРЕДЛОЖЕНИЯ

Одной из важнейших характеристик функции предложения является эластичность предложения. Эластичность предложения выражает характер зависимости относительного изменения объема предложения блага от относительного изменения его цены.

Коэффициент прямой эластичности предложения по цене показывает, на сколько процентов изменится объем предложения блага, если его цена изменится на один процент:

(4.10)
Если e_S > 1– предложение называется эластичным, если e_S < 1 – неэластичным и если е_S = 1 – единичным.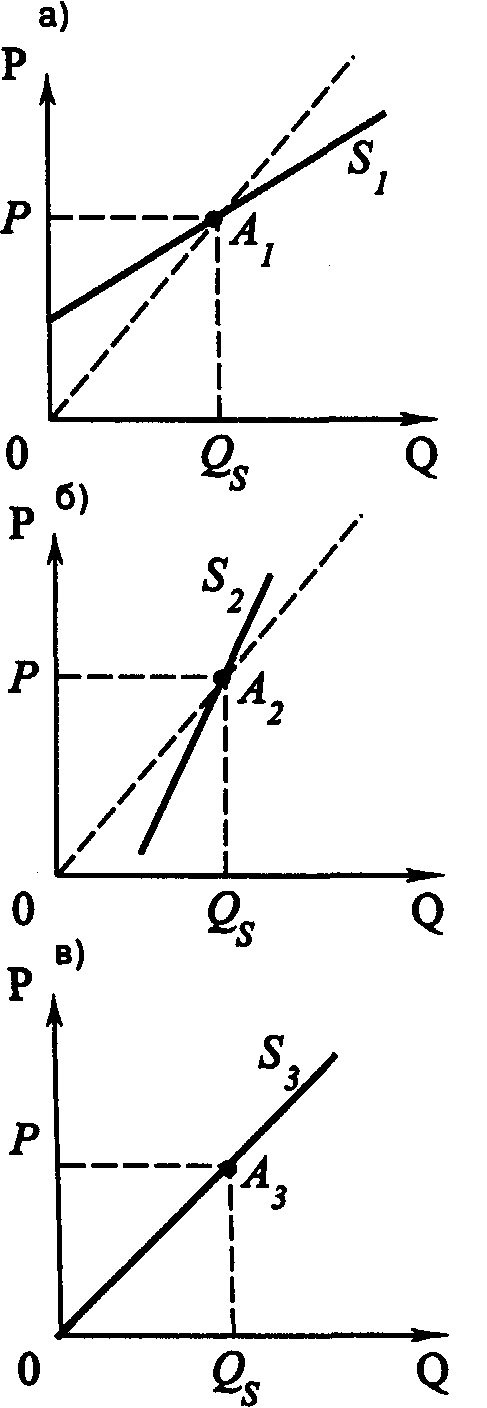


Рис. 4.16. Графическое определение ценовой эластичности предложения

Линейная кривая предложения, которая пересекает ось цен, эластична при всех ценах (рис. 4.16, а). Линейная кривая предложения, пересекающая ось объема продукции, неэластична при всех ценах (рис. 4.16, б). Если линейная кривая проходит через 0, то эластичность предложения равна 1 (рис. 4.16,в).

В случае многономенклатурного производства объем предложения каждого продукта зависит не только от его цены, но и от цен других продуктов, выпускаемых данной фирмой. Количественной характеристикой такой зависимости является коэффициент перекрестной эластичности предложения по цене (е_ij^S), который показывает, на сколько процентов изменится объем предложения блага i при изменении цены блага j на один процент:

(4.11)

Большинство совместно производимых благ для производителя взаимозаменяемы (е^S_ij < 0). Если е^S_ij> 0, то для производителя эти блага являются взаимодополняемыми.