Дубровский В.И., Федорова В.Н. Биомеханика. Учебник для вузов
 Скачать 6.47 Mb. Скачать 6.47 Mb.
|
5.8. Импульс тела. Импульс системы телСоотношение (5.6) между равнодействующей всех внешних сил и ускорением, которое она сообщает телу, можно преобразовать к виду, который оказывается полезным при решении многих задач: Выражение, стоящее в скобках называется импульсом тела. Импульсом тела называется векторная величина, равная произведению массы тела на скорость его центра масс. p = m∙v. (5.18) Размерность импульса в СИ — кг∙м/с. С учетом этого определения второй закон Ньютона (5.6) принимает вид: dp = F∙dt. (5.19) Произведение силы на время ее действия (F∙dt ) называется импульсом силы. Поэтому соотношение (5.19) читается так: изменение импульса тела равно импульсу действующей на него силы. Для решения практических задач соотношение (5.19) применяют к процессам малой длительности и записывают в следующем виде Δp = F-Δt. (5.20) Здесь Δр = р - р0— изменение вектора импульса, а Δt — длительность процесса. Пример Пусть человек массой 70 кг прыгает вверх с места. Скорость его центра масс при отрыве от земли равна 3,5 м/с, продолжительность фазы отталкивания Δt = 0,2 с. Определить силу, развиваемую мышцами ног при толчке. Решение. Начальная скорость равна нулю, поэтому р0= 0. В конечной фазе отталкивания импульс р = m·v = 70·3,5 = 245 кг·м/с и, следовательно, Δр = р — р0 = 245 кг·м/с. Используя (5.20), находим F = Δр/Δt = 245/0,2 = 1225 Н. Глава 6 ВИДЫ СИЛ В ПРИРОДЕ6.1. Гравитационные силы. Закон всемирного тяготенияВ природе существуют различные силы, которые характеризуют взаимодействие тел. Рассмотрим те силы, которые встречаются в механике. Гравитационные силы Вероятно, самой первой силой, существование которой осознал человек, являлась сила притяжения, действующая на тела со стороны Земли. И потребовались многие века для того, чтобы люди поняли, что сила тяготения действует между любыми телами. Первым этот факт понял английский физик Ньютон. Анализируя законы, которым подчиняется движение планет (законы Кеплера), он пришел к выводу, что наблюдаемые законы движения планет вокруг Солнца могут выполняться только в том случае, если между ними действует сила притяжения, прямо пропорциональная их массам и обратно пропорциональная квадрату расстояния между ними. Понимая, что планеты и Солнце ничем, кроме размеров и масс, не отличаются от других тел, Ньютон сформулировал закон всемирного тяготения. Любые два тела притягиваются друг к другу. Сила притяжения между точечными телами направлена по прямой, их соединяющей, прямо пропорциональна массам обоих тел и обратно пропорциональна квадрату расстояния между ними: Под точечными телами в данном случае понимают тела, размеры которых во много раз меньше расстояния между ними. Силы всемирного тяготения называют гравитационными силами. Коэффициент пропорциональности G называют гравитационной постоянной. Его значение было определено экспериментально: G = 6,7·10-11 Н·м2/кг2. Сила тяготения, действующая вблизи поверхности Земли, направлена к ее центру и вычисляется по формуле F = m·g.(6.2) где g — ускорение свободного падения. Роль силы тяготения в живой природе очень значительна так как от ее величины во многом зависят размеры, формы и пропорции живых существ. 6.2. Силы упругости. Закон Гука.Силы, действующие на тело, не только создают его ускорение, но и меняют его форму — создают деформацию. Например, если один конец пружины закрепить, а на другой конец подействовать силой F (потянуть рукой), то длина пружины увеличится на некоторую величину (х), после чего изменение длины прекратится, рис. 6.1. 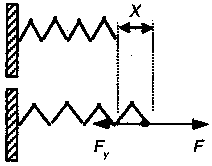 Рис. 6.1. Возникновение силы упругости Прекращение растяжения пружины объясняется тем, что при деформации пружины появляется сила, действующая в противоположную сторону и компенсирующая силу F. Сила, возникающая при деформации тела и направленная в сторону, противоположную смещению частиц тела, называется силой упругости (Fу). Сила упругости действует со стороны деформированного тела на тело, с которым оно соприкасается (в данном случае — со стороны пружины на руку). Растяжение или сжатие под действием приложенной силы испытывает не только пружина, но и все твердые тела. Английский ученый Роберт Гук экспериментально установил следующий закон. Сила упругости (F ), возникающая при малой (по сравнению с размерами тела) деформации, прямо пропорциональна величине деформации (х) и направлена в сторону, противоположную смещению частиц тела: Fу = — k·x. (6.3) Коэффициент пропорциональности k называется жесткостью тела (зависит от размеров, формы и материала). В СИ жесткость выражается в ньютонах на метр (Н/м). При сжатии динамометра, растяжении эспандера, прыжках на батуте возникает сила упругости. В некоторых случаях, например, при прыжке с трамплина (рис. 6.2), очень важен процесс восстановления формы деформированного тела. Так, при прыжках в воду используют упругий трамплин, который, распрямляясь, сообщает телу спортсмена дополнительную скорость и он прыгает выше (сила упругости деформированного трамплина совершает положительную работу). 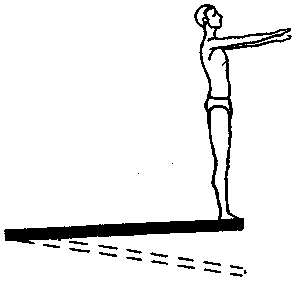 Рис. 6.2. Прыжок в воду с использованием трамплина |
