Иванов Е.А., Логика. Учебник Москва Издательство бек, 199 8
 Скачать 3.32 Mb. Скачать 3.32 Mb.
|
|
X
Знание отношений между сложными суждениями, как и между простыми, помогает правильно сочетать их в рассуждениях, избегать собственных ошибок и находить ошибки у оппонентов. Суждения, как и понятия, тоже могут подвергаться различным логическим операциям. Но если применительно к понятиям речь шла лишь об операциях с их содержанием и объемом (вспомним определение и деление, обобщение и ограничение понятий), то в отношении суждений дело обстоит гораздо сложнее. Логические операции с ними затрагивают и их типы и виды, и их субъектно-предикатную структуру и т. д. Среди таких операций выделяются две наиболее общие группы: преобразование простых и сложных суждений; отрицание тех и других суждений. Поскольку эти операции часто производятся в практике мышления, их логический анализ необходим в теоретическом отношении и важен в практическом.
Преобразование простых атрибутивных суждений. Простые атрибутивные суждения, заключая в себе определенный смысл, сами по себе не раскрывают полностью всей гаммы содержащихся в них взаимоотношений между их субъектом и предикатом, количеством и качеством. Например, известно, что «Все поэты— впечатлительные люди». Но «Все ли впечатлительные люди непременно поэты»? Перефразируя известную шутку: «Чтобы сделать рагу из зайца, надобно иметь как минимум кошку», спросим себя: «Чтобы числиться по разряду поэтов, достаточно ли слыть впечатлительным человеком?» Для выяснения точного логического смысла суждения нередко требуется преобразование его формы. Это достигается прежде всего посредством таких логических операций, как обращение, превращение, противопоставление субъекту и противопоставление предикату. Обращение (или конверсия). Это преобразование суждения путем перестановки его субъекта и предиката местами. При этом количество суждения (кванторное слово) может изменяться, а качество не меняется. Какие здесь действуют закономерности? Их три:а) обще утвердительное суждение (А) преобразуется в частноутвердительное (I). Обусловлено это тем, что субъект в нем распределен, а предикат, как правило, не распределен. Формула обращения: «Все S есть Р» — «Некоторые Р есть S». Так, в суждении «Все адвокаты — юристы» поставим субъект на место предиката, а предикат на место субъекта. В результате получим: «Некоторые юристы — адвокаты» (ибо юристами, как отмечалось, являются не только адвокаты, но и прокуроры, судьи, следователи и др.). Это графически можно представить так:
Такое преобразование называется «обращение с ограничением». Исключение составляет обращение общеутвердительных выделяющих суждений, в которых и субъект, и предикат распределены. Они обращаются в общеутвердительные же. Это «чистое обращение». Формула: «Все S (и только S) есть Р». Например: «Все люди — разумные существа»; «Все разумные существа — люди». Это видно на круговой схеме:  Все правильные определения, поскольку в них объем определяющего равен объему определяемого (правило соразмерности), тоже допускают лишь чистое обращение; б) частноутвердительное суждение (I) обращается в частноутвердительное (I). Субъект и предикат в них, как правило, не распределены. Формула обращения: «Некоторые S есть Р» — «Некоторые Р есть S». Пример: «Некоторые юристы — депутаты Государственной Думы» — «Некоторые депутаты Государственной Думы — юристы». На круговой схеме: Исключение составляют суждения, в которых субъект не распределен, а предикат распределен. В этих случаях частноутвердительное суждение преобразуется в общеутвердительное. Формула: «Некоторые S (и только S) есть Р».— «Все Р есть S». Пример: «Некоторые преступники — убийцы» — «Все убийцы — преступники». Это «обращение с приращением». Графически:  в) общеотрицательное суждение (Е) обращается в общеотрицательное (Е), так как субъект и’предикат здесь распределены. Формула: «Ни одно S не есть Р» — «Ни одно Р не есть S». Например: «Ни один свидетель не явился в суд» — «Ни один явившийся в суд не свидетель». Частноотрицательные суждения не обращаются. Субъект в них не распределен, следовательно, он не может стать предикатом нового, тоже отрицательного суждения, где предикат всегда распределен. Попробуем для примера выяснить, что произойдет с суждением «Некоторые мужчины — неженатые». Означает ли оно, что «Ни один женатый — не мужчина»? Или только «некоторые»? И тот и другой вывод бессмысленны. А иного сделать нельзя. Это видно на схеме: Какое значение имеет такая логическая операция, как об- . ращение, в практике мышления? Благодаря ей полнее раскрываются взаимоотношения между субъектом и предикатом суждения, а следовательно, связи и отношения между предметами мысли, отражаемыми в суждении. С субъекта, четко выраженного кванторным словом, наш взор переносится на предикат, который становится субъектом, а следовательно, обретает свое кванторное слово. Вспомним наши утверждения: «Всякое понятие выражается в слове, но не всякое слово выражает понятие» или «Всякое суждение есть предложение, но не всякое предложение есть суждение». Обращение может принимать и не столь развернутую, полную форму. Примером сокращенного обращения может служить поговорка: «Не все то золото, что блестит». Очевидно, это результат конверсии суждения: «Все то, что золото, блестит» (но «Не все то, что блестит, золото»). С помощью обращения проверяется правильность определений. Если после перестановки определяемого и определяющего смысл определения не меняется, значит, оно правильное. Нетрудно понять, что эту операцию можно производить и в юридической практике, когда требуется более точно выявить соотношения между теми или иными понятиями. Например: «Всякий закон есть нормативный акт», но «Не всякий нормативный акт есть закон» (есть еще указы, инструкции, правила и т. п.). Обращение играет незаменимую роль в проверке правильности юридических определений, от которых требуется особая точность. Превращение (обверсия). Это преобразование суждения путем перемены его качества на противоположное. Количество суждения, его субъект и предикат при этом не меняются. В превращении проявляются следующие закономерности: а) общеутвердительное суждение (А) преобразуется в общеотрицательное (Е). Формула превращения: «Все S есть Р» — «Ни одно S не есть не-Р». Так, суждение «Все адвокаты — юристы» по качеству утвердительное. Превращаем его в отрицательное, но так при этом, чтобы его смысл не изменился: «Ни один адвокат не является неюристом». Вот графическое изображение: 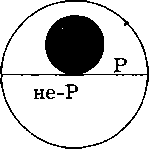 б) общеотрицательное суждение (Е), наоборот, превращается в общеутвердительное (А). Формула: «Ни одно S не есть не-Р» — «Все S есть Р». Пример: «Ни одно преступление не осталось нераскрытым» — «Все преступления раскрыты». Графически: 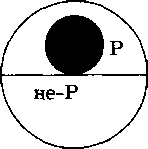 в) частноутвердительное суждение (I) превращается в частноотрицательное (О). Формула: «Некоторые S есть Р» — «Некоторые S не есть не-Р». Пример: «Некоторые свидетели дали верные показания» — «Некоторые свидетели не дали неверных показаний». Графически: 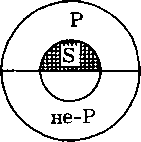 г) частноотрицательное суждение (О) превращается в частноутвердительное (I). Формула: «Некоторые S не есть Р» — «Некоторые S есть не-Р». Например: «Некоторые книги не есть интересные» — «Некоторые книги есть неинтересные». Графически: 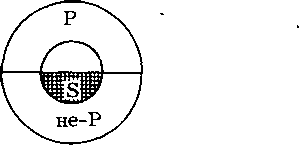 Значение превращения как логической операции состоит в том, что благодаря ему в суждении раскрывается новый, более богатый смысл: утверждение принимает форму отрицания и наоборот. Представим себе спор нескольких людей. Один говорит: «Петров — патриот». Другой возражает: «Петров —не патриот». Находится третий, который возражает второму: «Петров не является непатриотом». Высказанное им суждение и есть пример превращения. С одной стороны, оно равно-значно первому: двойное отрицание равно утверждению «Петров — патриот», а с другой — противоположно суждению «Петров — не патриот». В юридических дискуссиях, спорах и т. д. подобный прием используется нередко. О нем свидетельствуют, в частности, выражения типа: «не есть не ...», «не является не ...» и др. Обращение и превращение выступают основными, исходными логическими операциями с суждениями. Их различное сочетание порождает еще две операции: противопоставление субъекту и противопоставление предикату, которые считаются производными или смешанными. |

