Теплопроводность. УММ_МеТпл. Учебнометодические материалы по дисциплине
 Скачать 1.59 Mb. Скачать 1.59 Mb.
|
|
4.Порядок исследования Ознакомиться с целью, задачами работ и моделью. Получить варианты исследования (табл.1). Подготовить исходные данные согласно табл.2 и заготовить табл.3 и 4 для занесения результатов расчета. Для варианта «охлаждения пластины конвекцией» взять программу из файла «Лабораторные работы по МТ» / лабораторные работы №1 / ПЗ pas. Открыть ее с помощью turbo.exe. Для варианта охлаждения путем излучения брать программу П5pas. Ввести исходные данные варианта для среднего значения варьируемого параметра в программу значения S, To, α, или ε (если программа П5pas), подобрать ∆p и tk, производя пробные запуски программы F10 – run - enter. Построить кривые охлаждения Тоси(t,0), T (t, 0.5*S) и Tнов (t,S), на (рис.6), используя данные табл.3. Пример рис.6 показан ниже. 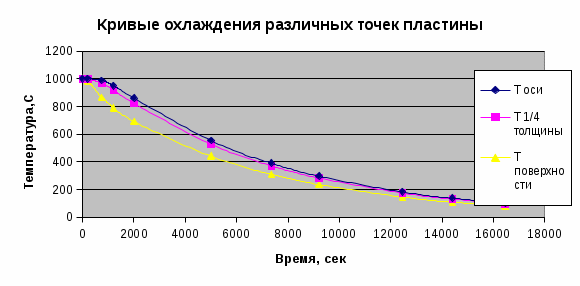 Рис. 6. Построить на рис.7 распределение температуры по толщине пластины, используя данные табл.4. Пример рис.7 показан ниже. 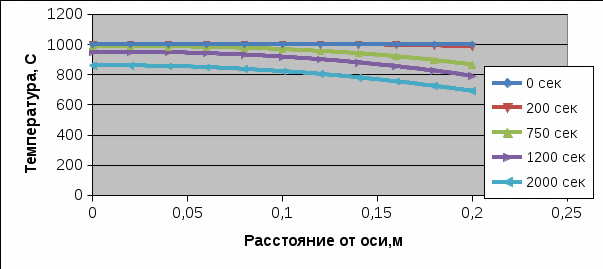 Рис.7. Распределение температуры по толщине пластины для 5-и моментов времени. Определить продолжительность охлаждения пластины до значения температуры оси 100 0С (t100) для трех значений варьируемого параметра ,построив график с тремя кривыми охлаждения оси пластины. Занести значения варьируемого параметра и соответствующие значения продолжительности охлаждения t100в табл. 5, пример которой приведен ниже. Таблица 5. Сводная таблица результатов определения времени охлаждения пластины до 100 °С при различных значениях параметра, например П=25, и результатов расчета по формуле (9).
Полученные данные по времени охлаждения аппроксимировать формулой : tохл =a* (П)n (6) где П – варьируемый параметр , например, П = 2.S, T0,α или ε. Коэффициенты формулы найдем, подставляя в формулу данные табл.5 (строки 1 и 3), например, П=2.S t100 =a*(2S1)n, t100 =a*(2S3)n. Решая полученную систему уравнений, получим формулы для определения 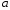 , n , n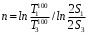 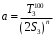 Рассчитаем n и 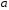 для приведенного примера, используя данные таблицы 5. для приведенного примера, используя данные таблицы 5.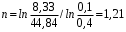 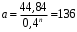 Рассчитаем время охлаждения по формуле (9) при полученных n и 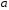 и запишем в таблицу 5. и запишем в таблицу 5.Построить зависимость по данным, полученным в табл.5, и по формуле (рис.6).На рисунке 8 изображен пример зависимости времени охлаждения пластины от толщины (2S), полученной по модели и по формуле (9). 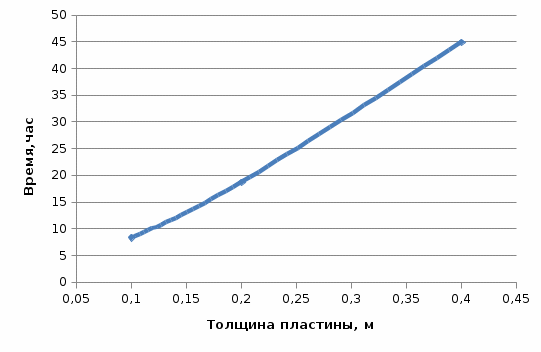 х – из таблицы 5, ------ - формула (6). Рис. 8 - Зависимость времени охлаждения изделия от толщины пластины до 100 °С. Сформулировать выводы о сделанной работе о полученных закономерностях охлаждения изученного объекта и о практической значимости полученной зависимости. Написать отчет по работе. Содержание отчета Титульный лист оформляется в соответствии с правилами, принятыми в ЧГУ, и содержат номер варианта задания. Цель и задачи работы. Таблица исходных данных (табл.2) Таблица результатов расчета температуры Тоси (t,0), (t,1/2S) , Tнов (t,S) для различных значений времен и (табл.3). Рис.6 с кривыми охлаждения 3-х точек температуры во времени , используя табл.3,дать анализ кривых. Таблица результатов расчета распределения температуры по толщине пластины ( узлы №№1.3.5.7.9.11) для 5 значений времени 0,1/8tk, 1/4 tk,1/2 tk и tk(табл.4). Рис.7 с распределением температуры по толщине пластины для пяти моментов времени, используя данные табл.4. Дать анализ динамики характера распределения. Таблица 5 с результатами расчета продолжительности охлаждения пластины для трех значений варьируемого параметра в заданном варианте. Формула t100 = a (П)n. Рис.8 со сравнением результатов расчета в табл.5 и по формуле. Выводы по работе. Например: Выполнено исследование влияния охлаждения конвекцией на продолжительность охлаждения пластины толщиной 0,4м до температуры 100°С. Результаты исследований аппроксимированной формулой 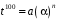 , где , где  =237, n=0,1 и могут быть использованы при определении продолжительности охлаждения плоского изделия до 100°С для =237, n=0,1 и могут быть использованы при определении продолжительности охлаждения плоского изделия до 100°С для  =250 =250 1000Вт/м2к. 1000Вт/м2к.Контрольные вопросы: Написать одномерное уравнение теплопроводности для пластины. Написать пример начального условия. Написать граничное условие – условие симметрии поля температуры по толщине пластины. Граничное условие III рода. Граничное условие при охлаждении путем измерения. Шаг выдачи на экран. Как производится пространственная дискретизация (понятие КХ) в МКР? Как производится дискретизация по времени (понятие t)? Как выглядит кривая охлаждения оси пластины? Как выглядит кривая охлаждения поверхности пластины? Как определяется продолжительность охлаждения пластины до 200°С? Литература: Кабаков З.К. и др. Технология математического моделирования металлургических процессов. Курс лекций: учебное пособие. – Череповец: ЧГУ, 2013.-75с. Лабораторная работа №3 Расчет расходов воды на секции зоны вторичного охлаждения Цель работы: Рассчитать расход воды на секции зоны вторичного охлаждения (ЗВО) МНЛЗ при заданной температурном режиме охлаждения заготовки в ЗВО Задачи работы: ознакомиться с математической моделью затвердевания и охлаждения слябов при НРС, определить коэффициенты теплоотдачи по секциям ЗВО, обеспечивающие рациональный температурный режим охлаждения поверхности слитка; определить расходы воды на секции ЗВО и общий расход воды на МНЛЗ; определить динамику и время затвердевания, глубину жидкой фазы. Математическая модель затвердевания и охлаждения слябового слитка при непрерывной разливке стали Описание процесса затвердевания и охлаждения слябов на МНЛЗ На рис. 1 показана схема технологической линии по формированию слябового слитка на вертикальной машине непрерывного литья заготовок (МНЛЗ). 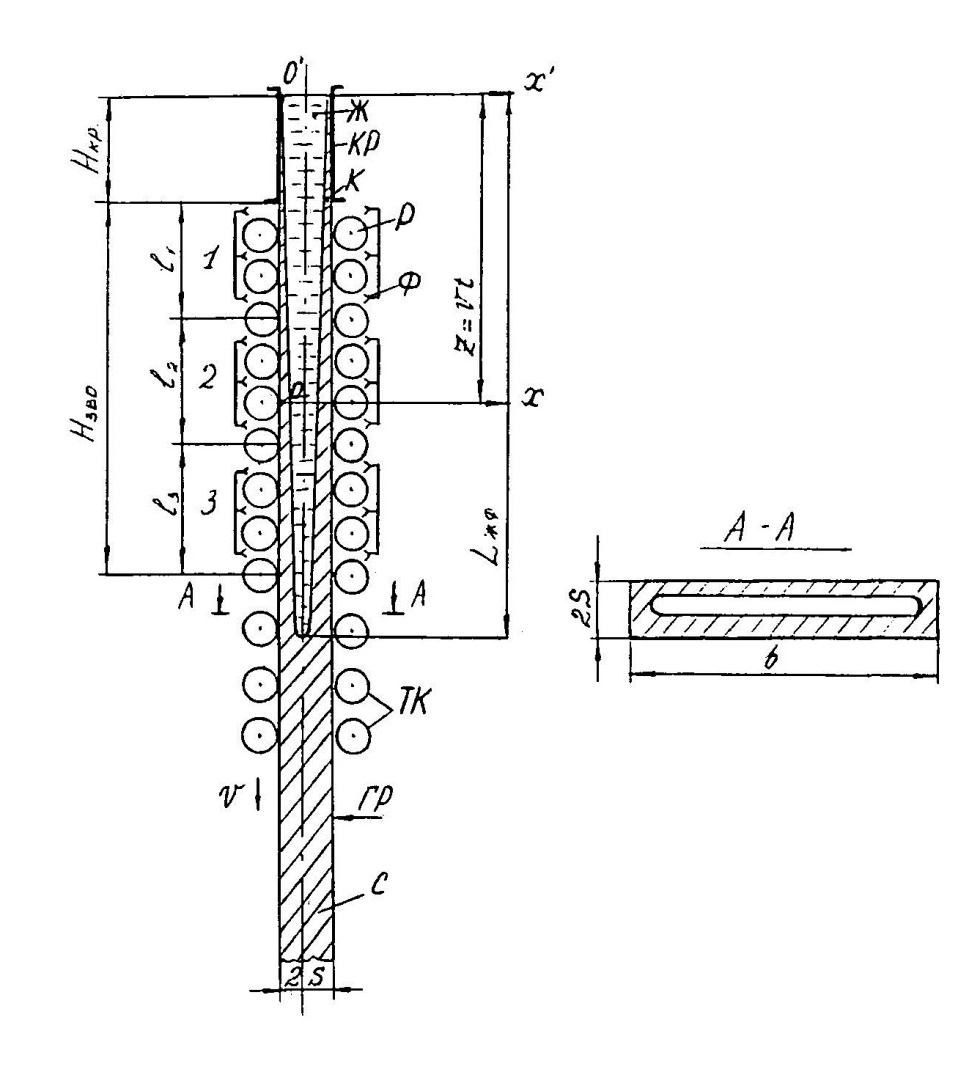 Рис. 1. Схема затвердевания и охлаждения слитка при непрерывной разливке стали на вертикальной МНЛЗ: с – слиток, к – корка, ж – жидкая стали, КР –кристаллизатор, ТК – тянущая клеть, Р – поддерживающие ролики, ГР – газорезка, Нкр – рабочая длина кристаллизатора, Нзво – длина зоны вторичного охлаждения, l1-l3 – длины секций ЗВО, Lжф – глубина жидкой фазы,  - направление скорости втягивания слитка, Ф – форсунки, ОХ’ и ОХ’ – начальное и промежуточное положение расчетного сечения в подвижной системе координат, 2S – толщина. - направление скорости втягивания слитка, Ф – форсунки, ОХ’ и ОХ’ – начальное и промежуточное положение расчетного сечения в подвижной системе координат, 2S – толщина.Слиток (с) условно разделен плоскостью, проходящей через середины широких граней. Жидкая сталь непрерывно поступает из промежуточного ковша через разливочный стакан в кристаллизатор (КР), в котором формируется наружная твердая оболочка (корка - К) слитка за счет отвода тепла в кристаллизатор и кристаллизации металла на рабочей поверхности кристаллизатора. Слиток в виде твердой оболочки (К) с жидким расплавом (Ж) внутри вытягивается из кристаллизатора и попадает в роликовую проводку, которая помогает оболочке сохранить прямоугольную при действии ферростатического давления форму. Проводка конструктивно выполнена из роликовых секций (1-3), поддерживающих широкие грани оболочки слитка. Роликовые секции, как правило, конструктивно по длине совпадают с секциями (1-3) зоны вторичного охлаждения, в которых поверхность слитка охлаждается с помощью водяных или водовоздушных форсунок. Длина проводки определяется глубиной жидкой фазы, а длина зоны вторичного охлаждения - предельным значением коэффициента теплоотдачи, выбираемым из условия плавного перехода кривой охлаждения поверхности слитка при переходе от принудительного охлаждения к естественному (путем свободной конвекции воздуха и излучением). В тянущую клеть (ТК) сечение слитка попадает полностью затвердевшим. После тянущей клети располагается участок газокислородной резки, где слиток разрезается на мерные “длины”. При разработке математической модели процесса затвердевания и охлаждения слябового слитка приняты следующие физические допущения: Процесс затвердевания слябового слитка можно считать одномерным и рассматривать только в плоскости, проходящей через середины широких граней. Процесс затвердевания при постоянной скорости литья – стационарный. Процессом молекулярной теплопроводности вдоль слитка можно пренебречь. Охлаждение слитка в кристаллизаторе происходит по закону Ньютона с заданным коэффициентом теплоотдачи. Охлаждение слитка в секциях ЗВО происходит по закону Ньютона с зависящим от расхода воды коэффициентом теплоотдачи. Охлаждение слитка на воздухе после ЗВО имитируется законом Ньютона со средним значением коэффициента теплоотдачи. Кристаллизация металла происходит с равномерным теплом в интервале температур ликвидуса и солидуса, соответствующих содержанию углерода и диаграмме Fe-С. С учетом этих допущений вместо стационарного процесса затвердевания металла в указанном сечении достаточно рассмотреть затвердевание расчетного (контрольного) сечения, перемещающегося вдоль слитка от мениска до газорезки с постоянной скоростью литья  (рис. 2). (рис. 2). 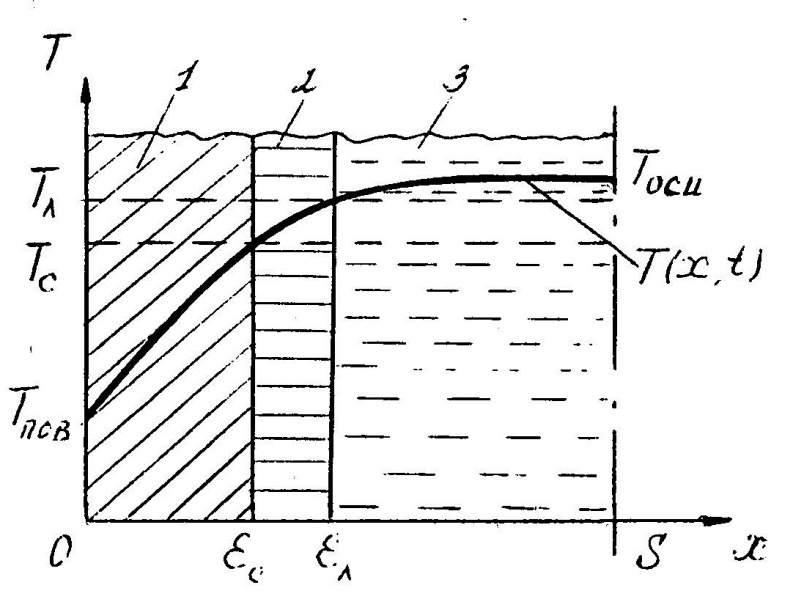 Рис. 2. Расчетное сечение слитка: 1 - твердая фаза (корка), 2 - двухфазная зона, 3 - жидкая фаза, Т (х, t) - распределение температуры. Расположение сечения на технологической линии определяется координатой 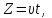 где t - текущее время затвердевания металла в рассматриваемом сечении. где t - текущее время затвердевания металла в рассматриваемом сечении. Математическое описание процесса затвердевания и охлаждения сляба на МНЛЗ. Математическое описание процесса затвердевания и охлаждения слитка включает одномерное уравнение теплопроводности, общее для жидкой, твердожидкой (двухфазной) и твердой зон, и учитывающее выделение тепла кристаллизации в интервале температур ликвидуса и солидуса: 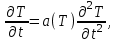 (1) (1)где 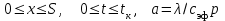 , ,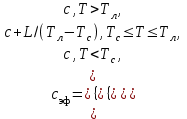 (2) (2)граничные условия типа Ньютона на охлаждаемой поверхности: 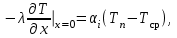 (3) (3)граничные условия в плоскости симметрии: 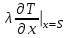 (4) (4)и начальное условие: 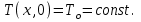 (5) (5)Здесь: S - половина толщины слитка, t - время, х - координата по толщине слитка, отсчитываемая от поверхности слитка в сторону плоскости симметрии (рис. П.1.2), 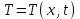 - распределение температуры по толщине слитка в момент времени t, а - температуропроводность, - распределение температуры по толщине слитка в момент времени t, а - температуропроводность, 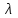 - теплопроводность, - теплопроводность, 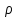 - плотность, с - теплоемкость твердой и жидкой фаз, L - удельная теплота кристаллизации, Тл и Тс - температуры ликвидуса и солидуса, сэф - эффективная теплоемкость, - плотность, с - теплоемкость твердой и жидкой фаз, L - удельная теплота кристаллизации, Тл и Тс - температуры ликвидуса и солидуса, сэф - эффективная теплоемкость,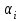 - коэффициент теплоотдачи на i-том участке охлаждения (кристаллизатор, секции ЗВО и участок охлаждения на воздухе), Тп - температура поверхности слитка в момент t, Тср - температура охлаждающей среды (вода, воздух), - коэффициент теплоотдачи на i-том участке охлаждения (кристаллизатор, секции ЗВО и участок охлаждения на воздухе), Тп - температура поверхности слитка в момент t, Тср - температура охлаждающей среды (вода, воздух), 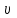 - скорость литья, - скорость литья, 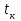 - заданный момент окончания процесса. - заданный момент окончания процесса.На участке первичного охлаждения - кристаллизатора - коэффициент теплоотдачи от поверхности слитка к воде определяется по эмпирической формуле: 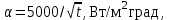 (6) (6)где 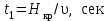 - продолжительность пребывания расчетного сечения в кристаллизаторе при скорости литья - продолжительность пребывания расчетного сечения в кристаллизаторе при скорости литья 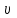 , Нкр - рабочая длины кристаллизатора (от мениска металла до нижнего края). Температура среды (воды) в кристаллизаторе принимается равной 30 , Нкр - рабочая длины кристаллизатора (от мениска металла до нижнего края). Температура среды (воды) в кристаллизаторе принимается равной 30 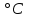 . .Коэффициент теплоотдачи от слитка к охлаждающей среде (воде) в i-той секции ЗВО определяется по эмпирической формуле: 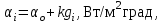 (7) (7)где 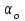 - эффективный коэффициент теплообмена излучением и свободной конвекцией при средней температуре поверхности слитка в ЗВО, k = 60, - эффективный коэффициент теплообмена излучением и свободной конвекцией при средней температуре поверхности слитка в ЗВО, k = 60, 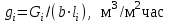 - удельный расход воды в i-той секции, - удельный расход воды в i-той секции, 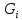 , , 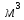 /час - общий расход воды на i-тую секцию ЗВО, /час - общий расход воды на i-тую секцию ЗВО, 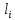 - длина i-той секции, b - ширина слитка. - длина i-той секции, b - ширина слитка.Формула (7) справедлива только для водяного форсуночного охлаждения. В случае использования водовоздушного охлаждения k = 100. Температура охлаждающейся среды (воды) в ЗВО принимается равной 30 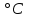 . .Коэффициент теплоотдачи при охлаждении слитка на воздухе находится по формуле: 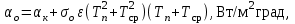 (8) (8)где 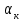 - коэффициент теплообмена конвекцией (7-10 Вт/м2град), - коэффициент теплообмена конвекцией (7-10 Вт/м2град), 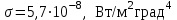 - коэффициент излучения абсолютно черного тела, - коэффициент излучения абсолютно черного тела,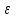 - степень черноты поверхности слитка (для литой окисленной поверхности - степень черноты поверхности слитка (для литой окисленной поверхности 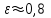 . .В формулу (8) средняя температура поверхности слитка при охлаждении на воздухе и температура среды (воздуха) подставляются в К. 1.3 Численная модель процесса затвердевания. Система уравнений (1)-(5) решена численным методом конечных разностей. В этом методе вводится дискретизация пространства и времени (п,1.3). Вместо непрерывного поля температуры Т(х,t) рассматривается дискретное поле 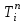 в точках расчетной области (рис. 3), расположенных с шагом в точках расчетной области (рис. 3), расположенных с шагом 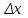 . . 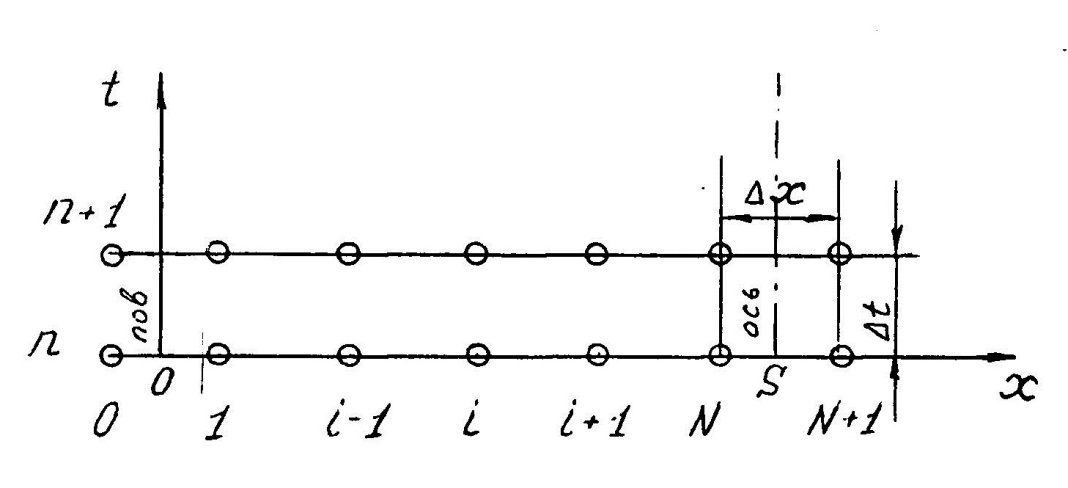 Рис. 3. Схема дискретизации области переменных (х, t): i - индекс (номер) узла, n - индекс момента времени, 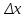 и и 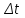 - шаги дискретизации пространства и времени. - шаги дискретизации пространства и времени.Время течет дискретно с шагом 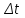 . С помощью метода конечных разностей получен алгоритм решения (дискретный аналог приведенной выше математической модели) или так называемая численная модель. . С помощью метода конечных разностей получен алгоритм решения (дискретный аналог приведенной выше математической модели) или так называемая численная модель.Модель включает формулы для расчета в момент времени 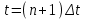 : поля температуры : поля температуры 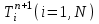 во внутренних узлах (точках) расчетной области по известному полю температуры во внутренних узлах (точках) расчетной области по известному полю температуры 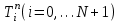 в предыдущий момент времени в предыдущий момент времени 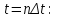 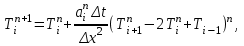 (9) (9)где i = 1, ... N, - температуры в фиктивном узле i =0: 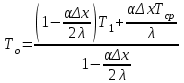 - в фиктивном узле i = N+1: 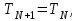 а также координату расположения расчетного сечения на технологической оси МНЛЗ: 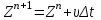 и координату изотермы солидуса в расчетном сечении слитка: 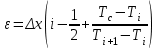 при 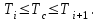 Здесь 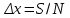 , где N - количество внутренних узлов, S - половина толщины слитка, , где N - количество внутренних узлов, S - половина толщины слитка, 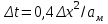 , ам - максимальное значение температуропроводности, , ам - максимальное значение температуропроводности, 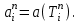 Полю температуры  соответствует начальное поле со значением соответствует начальное поле со значением  . . Алгоритм запрограммирован на языке ПАСКАЛЬ (программа ZBOCALK). В табл. П.1.1 приведены идентификаторы исходных данных к этой программе. Результаты моделирования выводятся на экран через равные интервалы длины секции в следующем порядке: текущее время процесса в сек. и мин, расстояние от мениска в м, расстояние от шага секции в м, температура поверхности в 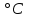 , ,температура оси слитка в 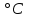 , ,координата изотермы солидуса в нем (толщина корочки по солидусу), номера узлов расчетной сетки и их координаты в мм, значения температуры в узлах сетки в 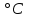 . .Таблица 1 |
