СД.ДС.Ф.1 .Управление процессами. Учебнометодический комплекс дисциплины Управление процессами Специальность подготовки 080507. 65 Менеджмент организации
 Скачать 2.03 Mb. Скачать 2.03 Mb.
|
Лекция 11. Управление очередями (3 часа)Очереди (Queues) и управление ими — один из важнейших аспектов операционного менеджмента. Знать, как обращаться с ними, необходимо при составлении графиков, проектировании операций, планировании товарно-материальных запасов и т.д. Сегодня каждый человек пользуется услугами сервисных фирм, и нам приходится стоять в очередях практически ежедневно: то ли в автомобильной "пробке", добираясь на работу, то ли к кассе супермаркета. Очереди существуют и на производственных предприятиях: детали должны ждать обработки на том или ином станке, а станки ждут своей очереди на капитальный ремонт. Иными словами, очереди вездесущи. В данном дополнении рассматриваются основные аспекты проблемы очередей и приводятся стандартные формулы для решения задач, связанных с управлением очередями. Эти формулы, разработанные на основе теории очередей, позволяют плановикам анализировать сервисные потребности и планировать пропускную способность сервисных предприятий в соответствии с конкретными условиями. Теория массового обслуживания, в которой исследуются проблемы очередей, достаточно широка: она охватывает такие непохожие виды ожидания, как очередь к кассе универсама и пребывание самолета в полете в ожидании свободной посадочной полосы. Достаточно вспомнить, например, что в последние годы многие провайдеры глобальной сети Internet столкнулись с проблемой недостатка модемных линий для своих пользователей. Такую ситуацию также можно проанализировать с помощью моделей массового обслуживания. Экономическая сущность проблемы очередей Практически в любой ситуации, связанной с очередями, основным является поиск компромиссного решения. Менеджер должен оценить, как соотносятся между собой дополнительная стоимость, необходимая для ускорения процесса обслуживания (например, строительство дополнительных автомобильных полос и посадочных полос в аэропорту, добавление пунктов расчета в универмаге и т.п.), и издержки, связанные с ожиданием в очереди. В реальных условиях принятие компромиссного решения в задачах массового обслуживания часто не такая уж сложная проблема. Так, например, если в результате анализа выясняется, что общее время, которое проводят служащие компании, ожидая очереди к копировальному аппарату, можно использовать на выполнение основных операций, руководству следует сравнить затраты на установку дополнительного ксерокса со стоимостью сэкономленного благодаря этому рабочего времени. Результаты такого анализа легко представляются в денежном выражении, и принятие компромиссного решения в этом случае будет достаточно легкой задачей. В больнице также существует проблема очереди пациентов, которая связана с потребностью в койко-местах. Для решения этой проблемы можно расширить больницу и вычислить стоимость дополнительных койко-мест, сложив стоимости строительства новых помещений, дополнительного оборудования и суммы, на которую повысятся затраты на содержание больных. Но что же будет противовесом стоимости дополнительных койко-мест? В данном случае приходится сталкиваться с тем, что трудно найти денежный эквивалент, отображающий потребность пациента в больничной койке. Действительно, утрачиваемую прибыль больницы оценить можно, но как быть с потерями гуманитарного характера, связанными с неполноценным медицинским обслуживанием? Соотношение между затратами и пропускной способностью системы обслуживания На рис. для устойчивого потока клиентов показаны зависимости затрат, связанных с обслуживанием очереди, от увеличения пропускной способности системы обслуживания. 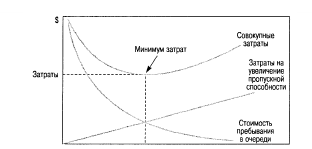 Рис. Определение оптимальной пропускной способности канала обслуживания При малой пропускной способности канала обслуживания стоимость пребывания в очереди максимальна. По мере увеличения пропускной способности количество клиентов в очереди и время их ожидания сокращаются, что приводит к снижению затрат, связанных с очередями. Аппроксимацию затрат пребывания в очереди часто представляют в виде отрицательной экспоненциальной функции. Затраты на увеличение пропускной способности возрастают равномерно и ступенчато, но для упрощения в данном примере они отображены линейной функцией. Совокупные или суммарные затраты имеют вид U-образной кривой, характерной для задач, связанных с уравновешиванием показателей. Оптимальные затраты соответствуют точке пересечения кривой стоимости пребывания в очереди и затрат на увеличение пропускной способности. Практическое значение очередей Прежде чем перейти к подробному рассмотрению основ теории очередей, рассмотрим проблему очередей с качественной стороны. На рис. показан входящий поток заявок на обслуживание сервисного предприятия (например, банка) и сервисные возможности этого предприятия (например, количество кассиров и банковских служащих по предоставлению ссуд). 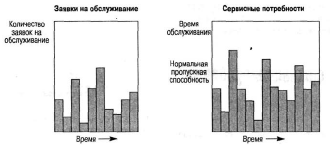 Рис.Заявки на обслуживание 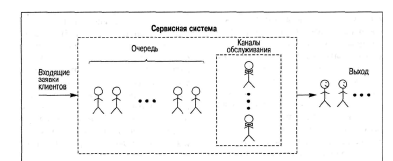 Рис.. Компоненты системы массового обслуживания Одной из важнейших переменных является объем входящего потока заявок за конкретный период времени работы сервисной системы. В системе предоставления услуг изменение потребительского спроса приводит к изменению объема оказываемых услуг, часто превышая нормальную пропускную способность. Существует несколько способов управления входящими потоками. Так, например, можно намеренно сократить длину очереди (например, отвести несколько площадок в ресторане, специализирующемся на обслуживании в автомобилях); ввести конкретные часы для конкретных категорий посетителей, предложить специальные услуги. Если же говорить о собственно каналах обслуживания, то можно влиять на время обслуживания, используя для этого более быстрые или медленные каналы, разное оборудование, инструментарий, материалы, разное расположение помещений, разное время наладки оборудования и т.д. Существование очередей — это нормальное состояние производственной системы; ими довольно эффективно можно управлять с помощью средств системного менеджмента и проектирования. Известный исследователь теории очередей профессор Ричард Ларсон (R.M. Larson) и его коллеги предложили очень полезные рекомендации для управления очередями, основанные на результатах изучения работы банков (врезка "Рекомендации по управлению очередями"). Система массового обслуживания Как видно из рис., типичная система массового обслуживания (Queuing System) состоит из трех основных компонентов: исходной генеральной совокупности (Source Population) пользователей (клиентов) рассматриваемой сервисной системы; сервисной системы; сценариев выхода клиентов из сервисной системы (возвратиться обратно в исходную генеральную совокупность или покинуть ее?). Рекомендации по управлению очередями Ниже представлены весьма полезные рекомендации для управления очередями, вытекающие из анализа количественных моделей очередей. 1. Определите приемлемое время ожидания для своих клиентов. Сколько готовы ждать ваши клиенты? На основе этой оценки определите требования к операциям. 2. Постарайтесь отвлекать внимание клиентов в процессе ожидания в очереди. Проигрывая музыку, показывая фильм по видео или развлекая клиентов каким-либо еще способом, вы сможете отвлечь их внимание от мыслей о необходимости стоять в очереди. 3. Информируйте клиентов о ситуации. Это особенно важно, если очередь превышает обычные размеры. Объясните клиентам причину сложившейся ситуации и расскажите, что конкретно делается для ускорения процесса обслуживания. 4. Не размещайте служащих, не занимающихся непосредственным обслуживанием клиентов, на виду очереди. Ничто так не раздражает людей в очереди, как вид работников, которые потенциально могли бы их обслуживать, но занимаются другими делами. 5. Разбейте очередь. Если можно выделить группу клиентов, обслуживание которых занимает немного времени, объедините их в отдельную очередь, чтобы их не задерживали те, на работу с которыми потребуется много времени. 6. Подготовьте обслуживающий персонал к работе с людьми, научите его быть вежливым и дружелюбным. Обращение к клиенту по имени или какие-либо другие индивидуальные знаки внимания очень способствуют устранению негативной атмосферы в длинной очереди. (Практическая рекомендация: вместо того чтобы просто учить служащих "быть дружелюбными", психологи советуют указывать, в какие именно моменты следует показывать свое доброе отношение, например улыбаться: при приветствии клиента, при приеме заказа или при расчете у кассы). Тесты с использованием специальных поведенческих моделей подтвердили, что в этом случае клиенты намного позитивнее воспринимают дружелюбное отношение обслуживающего персонала. 7. Стимулируйте посещение предприятия в периоды затишья. Информируйте клиентов о времени, когда у вас практически не бывает очередей; сообщайте им и о периодах, когда наплыв посетителей особенно велик. Это позволит вам сгладить нагрузку. 8. Подходите к задаче сокращения очередей с точки зрения перспективы. Разрабатывайте планы альтернативных способов обслуживания клиентов. Если возможно, разработайте планы автоматизации или ускорения процесса обслуживания. Это однако не означает, что автоматизацию следует проводить за счет сокращения индивидуального внимания к посетителям, поскольку некоторые клиенты ждут от сервисного предприятия, кроме всего прочего, еще и доброго отношения. Входящий поток заявок клиентов Источником входящего потока заявок в сервисную систему может быть конечная или бесконечная генеральная совокупность (популяция) клиентов. Такое разграничение необходимо, поскольку анализ конечной и бесконечной генеральных совокупностей основывается на различных исходных предпосылках и проводится с использованием разных уравнений и формул. 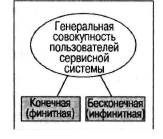 Конечная генеральная совокупность Термином конечная генеральная совокупность (популяция) описывается ограниченная совокупность пользователей, которые время от времени будут создавать очереди. Конечная генеральная совокупность характеризуется тем, что, когда пользователь покидает свое место в исходной совокупности (например, станок ломается и нуждается в ремонте) и число пользователей в исходной генеральной совокупности сокращается на одну единицу, это приводит к снижению вероятности появления следующей заявки на обслуживание. И наоборот, после того как клиент обслужен, генеральная совокупность снова увеличивается и вероятность появления заявки на обслуживание возрастает, так как в будущем этому клиенту вновь может потребоваться данная услуга. Для решения задач такого рода необходим набор формул, отличный от тех, которые применяются при анализе бесконечной генеральной совокупности. Рассмотрим следующий пример. Представьте себе мастерскую, в которой находится шесть станков, обслуживаемых одним ремонтным рабочим. Если ломается один станок, исходная генеральная совокупность уменьшается до пяти станков, и вероятность поломки одного из исправных станков будет, конечно, несколько ниже, чем для шести работающих станков. Если же поломаются сразу два станка и останутся работать только четыре, вероятность следующей поломки снижается еще больше. И наоборот, после того как станок отремонтирован и начинает вновь работать, конечная генеральная совокупность станков увеличивается, увеличивая соответственно вероятность следующей поломки. Модель конечной генеральной совокупности с одним каналом обслуживания, которая может применяться для анализа ситуаций такого характера. Бесконечная генеральная совокупность Предполагается, что бесконечная генеральная совокупность пользователей настолько велика, что изменение ее размеров вследствие прибытия (т.е. появления клиента, который нуждается в услуге) или возвращения обслуженного клиента в свою исходную совокупность не оказывает существенного влияния на вероятность появления заявки на обслуживание. Если бы в мастерской, в рассмотренном выше примере, было не шесть, а 100 станков, то при поломке одного или двух из них вероятность выхода из строя следующего изменилась бы совсем незначительно, и при анализе ситуации можно было бы с малой погрешностью исходить из предположения, что данная генеральная совокупность практически является бесконечной. Формулы для решения задач, связанных с "бесконечными" очередями, могут применяться, например, при анализе работы врача, обслуживающего 1000 пациентов, или крупного универмага с потоком в 10 тысяч покупателей. Распределение входящего потока Для выбора параметров системы управления очередями вначале следует определить способ, с помощью которого ожидающие заявки (требования) организуются для последующего обслуживания. В формулах для анализа очередей используется такой показатель, как интенсивность входящего потока (Arrival Rate), т.е. количество поступивших заявок за определенный период времени (например, среднее число заявок за полгода). На практике различают равномерное и произвольное распределения поступающего потока заявок. Равномерное распределение входящего потока характеризуется строгой периодичностью, т.е. равными интервалами времени между подряд идущими входящими заявками. В производственных системах такими потоками могут быть только ритмичные процессы и ими можно управлять автоматически. Значительно шире распространено произвольное (переменное) распределение входящих потоков заявок, которое обсуждается ниже. При рассмотрении входящих потоков заявок в сервисную систему следует учитывать два основных момента. Во-первых, необходимо проанализировать интервалы времени между двумя следующими подряд входящими заявками и определить закон их статистического распределения. Обычно принимается, что интервалы между поступающими заявками на обслуживание распределяются экспоненциально. Во-вторых, можно установить определенный период времени Ф и попытаться определить, сколько заявок может поступить в систему за этот период Т. Для этого чаще всего используется распределение Пуассона. Экспоненциальное распределение Если заявки на обслуживание поступают в сервисную систему абсолютно произвольно, временные интервалы между соседними заявками распределяются по экспоненциальному закону (Exponential Distribution). 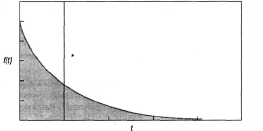 Рис. Экспоненциальное распределение Функция распределения вероятностей в таком случае имеет вид 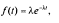 где — среднее количество заявок, поступающих за определенный период времени. Интегрируя кривую, т.е. 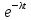 , в области положительных значений, можно вычислить , в области положительных значений, можно вычислить вероятность появления входящих заявок за определенный период времени. Так, например, при условии поступлении в очередь одной заявки в единицу времени ( = 1) можно образовать приведенную ниже таблицу, значения для которой либо получены из формулы 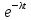 , либо взяты из Приложения F. Во втором столбце этой таблицы приведены вероятности того, что следующая входящая заявка поступит более чем через t минут после предыдущей. В третьем столбце приведены вероятности появления следующей входящей заявки в течение t минут (они вычисляются вычитанием из столбца 1 значений столбца 2). , либо взяты из Приложения F. Во втором столбце этой таблицы приведены вероятности того, что следующая входящая заявка поступит более чем через t минут после предыдущей. В третьем столбце приведены вероятности появления следующей входящей заявки в течение t минут (они вычисляются вычитанием из столбца 1 значений столбца 2).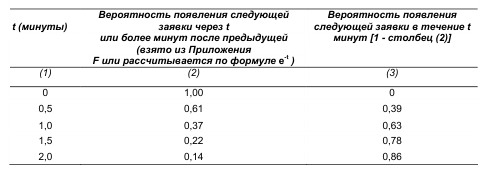 Распределение Пуассона Чтобы найти число поступающих заявок в течение определенного периода Т, необходимо воспользоваться распределением Пуассона, приведенным на рис. Оно получено вычислением вероятности появления n событий (заявок) в течение периода Т при условии, что появление событий носит произвольный характер. Закон распределения вероятностей Пуассона описывается формулой Применительно к рассматриваемой проблеме очередей формула отображает вероятность поступления конкретного числа n входящих заявок за определенный период времени T1. Так например, если средняя интенсивность входящего в систему потока равна трем заявкам в минуту (λ = 3) и нужно определить вероятность того, что в течение минутного периода в систему поступят именно пять заявок (λ = 5, Т= 1), то получаем Следовательно, в любой минутный интервал в сервисную систему поступает 5 заявок с вероятностью 10,1%. Распределение Пуассона графически чаще отображается в виде плавной кривой, как, например, показано на рис, однако фактически оно дискретно. (Кривая сглаживается в большей мере при увеличении значения п.) Рассматриваемое нами распределение может быть только дискретным, поскольку n в рассматриваемом случае обозначает количество заявок, поступающих в сервисную систему, а следовательно, обязательно должно быть целым числом (например, не может быть 1,5 заявки). Обратите также внимание, что экспоненциальное и пуассоновское распределения взаимосвязаны. Среднее значение и дисперсия распределения Пуассона одинаковы и равны λ . Среднее значение экспоненциального распределения равно а дисперсия — (Нужно помнить, что интервалы между двумя входящими заявками распределяются экспоненциально, а количество заявок в единицу времени — в соответствии с распределением Пуассона.) Другие характеристики входящих потоков Другими важными характеристиками входящих потоков являются: вид входящего потока (Arrival Pattern), размер единицы входящего потока заявок (Arrival Unit) и уровень терпеливости клиентов (Degree Of Patience) (рис. 5.6). Bug входящего потока Входящие в систему потоки намного лучше поддаются управлению, чем принято считать. Так, например, парикмахер может снизить интенсивность входящего потока в субботу (и, чаще всего, переместить его на другие дни недели), увеличив цену стрижки взрослого посетителя на 1 доллар или взимая за стрижку ребенка "взрослую" цену. Магазины проводят сезонные распродажи в периоды затишья или однодневные распродажи частично для регулирования потока покупателей. С такой же целью авиалинии предлагают своим пассажирам сезонные скидки и сниженные расценки для туристов. Проще всего управлять входящими потоками, назначив конкретные часы работы предприятия. Однако следует помнить, что в некоторых сервисных организациях спрос неуправляемый, как, например, потребность в неотложной медицинской помощи в городской больнице. Однако даже в таких ситуациях входящими потоками в пункты скорой помощи конкретных больниц в некоторой степени можно управлять, например, информировать водителей машин, работающих в конкретном районе, о степени загруженности разных больниц. Единица входящего потока Одиночная заявка рассматривается как единица измерения потока (т.е. наименьшее возможное число). Так, например, одиночная заявка на Нью-йоркской фондовой бирже составляет пакет из 100 акций; одиночная заявка потока на яйцеперерабатывающей фабрике может быть как десяток яиц, так и лоток на 2,5 десятка яиц; одиночная заявка в ресторан — один посетитель. Групповая заявка включает в себя множество единиц, например, лот акций из 10 пакетов (1000 акций), ящик из лотков яиц или компания из пяти человек, пришедшая в ресторан. 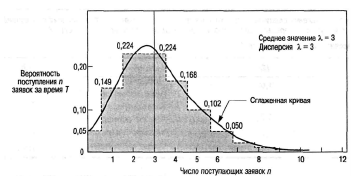 Рис. Распределение Пуассона 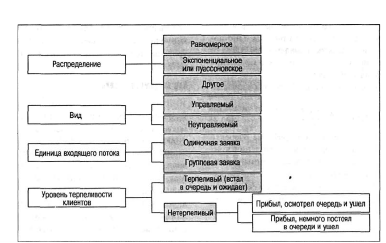 Уровень терпеливости Терпеливой называют заявку клиента, который будет ожидать момента оказания услуги сервисным предприятием столько времени, сколько необходимо. В соответствии с теорией очередей, даже если клиент ведет себя нетерпеливо и выражает свое недовольство, уже тот факт, что он тем не менее продолжает ожидать, позволяет назвать его терпеливым. Существует два типа нетерпеливых входящих потоков. Клиенты (заявки) первого типа прибывают в систему обслуживания, осматривают ее и очередь и решают немедленно уйти. Ко второму типу относятся те, кто прибывает, знакомится с ситуацией, становится в очередь и затем, постояв некоторое время, все же уходит. Поведение первого типа называют неприсоединением к очереди (Balking), а второго — переоценкой условий ожидания (Reneging). Характеристика очередей Как уже отмечалось, основными элементами системы массового обслуживания являются очереди (или несколько очередей) и имеющиеся в наличии каналы обслуживания. Ниже описываются основные характеристики очередей и правила управления ими, а также анализируются структуры очередей. Параметры очередей Основными характеристиками очередей являются: длина очереди, количество очередей ("хвостов") и дисциплина очереди. Длина очереди С практической точки зрения бесконечной называется любая очередь, длина которой по сравнению с пропускной способностью сервисной системы очень велика. Возможными примерами бесконечной очереди могут быть дорожные пробки, растянувшиеся на несколько километров, либо очередь в театральную кассу на несколько кварталов. Автозаправочные станции, загрузочные доки и автомобильные стоянки имеют ограниченную пропускную способность обслуживания очередей, которая регулируется юридическими нормами или техническими возможностями. Ограниченная пропускная способность накладывает отпечаток на управление очередями и одновременно вызывает перераспределение входящего потока. Клиенты, которым было отказано во вхождении в конкретную очередь вследствие недостатка места, могут присоединиться к данной генеральной совокупности позднее, а могут найти другую сервисную систему и выйти из генеральной совокупности рассматриваемой сервисной системы. И такие действия клиентов приводят к совершенно разным результатам. В диснеевских тематических парках в Орландо, штат Флорида, длинными очередями управляют с помощью веревочных заграждений. Развешенные плакаты содержат информацию о приблизительном времени ожидания, а по телевизионным мониторам транслируются кино и клипы для ожидающих посетителей. По мере продвижения вперед люди попадают в самые разные условия: проходят под несущимися железнодорожными вагонами, через таинственные пещеры или через залы, демонстрирующие лучшие старые фильмы. http://www.disney.com Количество очередей Очередь называется однолинейной, если сервисная система работает с одной очередью, выстроенной в одну линию. Многолинейные очереди состоят из двух или нескольких однолинейных очередей, образующихся к двум или нескольким каналам обслуживания. К ним относятся также несколько однолинейных очередей, соединяющихся в определенной точке перераспределения в одну линию. Особенностью многолинейных очередей на перегруженных сервисных предприятиях является то, что они не постоянны и часто смещаются, например, если несколько заявок поступили через короткие интервалы, то одна очередь может оказаться более длинной, чем другие, и клиенты переходят из нее в более короткие. То же самое происходит, если очевидно, что на обслуживание клиентов, стоящих в других очередях, требуется меньше времени. 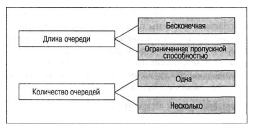 Дисциплина очереди Дисциплиной очереди называют правило или набор правил, определяющих приоритетный порядок обслуживания клиентов в очереди. Выбранные предприятием правила могут оказать весьма серьезное влияние на общую производительность сервисной системы. От правил назначения приоритета зависит количество клиентов в очереди, среднее время ожидания, диапазон варьирования длины очереди, продуктивность работы сервисного предприятия и многое другое. Наиболее распространенным правилом назначения приоритета является правило первым прибыл, первым обслужен (First Come, First Served — FCFS). Согласно ему клиенты в очереди обслуживаются в хронологическом порядке прибытия, и никакие другие характеристики на порядок обслуживания влияния не оказывают. Это правило считается самым справедливым, однако на практике оно зачастую приводит к дискриминации тех клиентов (заявок), время обслуживания которых намного короче времени обслуживания других. Другими примерами правил назначения приоритета являются: первоочередное обслуживание по предварительным заказам, первоочередное обслуживание в случаях крайней необходимости, первоочередное обслуживание наиболее доходных клиентов, первоочередное обслуживание самых больших заказов, первоочередное обслуживание постоянных клиентов, первоочередное обслуживание клиентов, ожидавших в очереди наибольшее время, и обслуживание по ближайшей обещанной дате. В реальных условиях могут применяться сразу несколько приоритетов, выстраиваемых в порядке значимости. 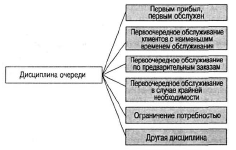 При использовании любого из этих правил возникает две основные проблемы практического характера. Первая заключается в том, что о них необходимо проинформировать клиентов с тем, чтобы они могли им следовать, а вторая — в необходимости создании специальной системы, позволяющей служащим управлять такими очередями (например, ввести номерную систему). Распределение времени обслуживания Еще одной важной характеристикой очереди является время, которое клиент или единица потока (заявка) проводит в контакте с каналом обслуживания от начала процесса обслуживания. В рассмотренных выше формулах использовалась интенсивность обслуживания, определяемая как пропускная способность канала обслуживания в количествах единиц потока за определенный период времени (например, 12 завершенных операций в час), а не как время обслуживания, которое для данного примера в среднем составляет пять минут. Если каждое обслуживание имеет одну и ту же продолжительность, то говорят о правиле постоянного времени обслуживания. Соблюдение этого правила (так же как неизменный интервал поступления заявок) чаще присуще только автоматически выполняемым операциям. Если же время обслуживания имеет произвольную величину, то для его описания используют закон экспоненциального распределения. Исходя из него определяют среднее число, обозначаемое м, единиц потока (заявок) или клиентов, которые могут быть обслужены в течение этого периода. Структура очередей Как видно из приведенного ниже рисунка, поток заявок, подлежащих обслуживанию, может проходить через одну очередь, через несколько очередей либо через комбинацию этих двух вариантов. Выбор формата структуры частично зависит от количества клиентов (заявок), нуждающихся в обслуживании, и частично — от ограничений, связанных с конкретным порядком, в котором должно проводиться обслуживание. Одноканальная, однофазовая структура Это самый простой тип структуры очереди и, если входящие потоки и процесс обслуживания описываются стандартными распределениями, то существуют простые формулы для решения соответствующих задач. Если же эти распределения нестандартные, то такие задачи относительно легко решаются с помощью компьютерного моделирования. Типичным примером одноканальной и однофазовой структуры может служить парикмахерская с одним парикмахером. Одноканальная, многофазовая структура В качестве иллюстрации такой структуры можно привести станцию для мойки автомобилей, поскольку в ходе этого обслуживания выполняется целый ряд сервисных операций в относительно стабильной последовательности: чистка пылесосом, увлажнение, мытье, ополаскивание, сушка, мойка окон и парковка. Основным показателем одноканальной, многофазовой структуры обслуживания с определенной последовательностью услуг является объем накопления единиц потока (заявок) перед каждой операцией, где также образуются свои отдельные очереди. 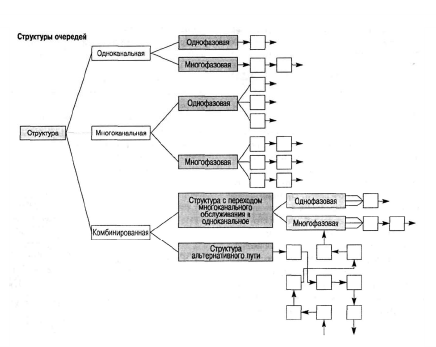 Многоканальная, однофазовая структура Примерами такого типа структуры могут служить очереди к окнам банковских клерков или к кассам в крупных магазинах. Особенностью данной структуры является то, что вследствие неравномерного времени обслуживания каждого клиента очереди продвигаются с разной скоростью. При этом некоторые клиенты, прибывшие в систему позже, обслуживаются раньше тех, кто пришел первым. Это приводит также к определенному перераспределению очередей, произвольно осуществляемому клиентами. Для того чтобы соблюдать правило обслуживания клиентов в хронологическом порядке их прибытия, необходимо предварительно сформировать одноканальную очередь, в которой, как только освобождается один из каналов обслуживания, обслуживается следующий в очереди клиент. Основная проблема такого формата обслуживания состоит в том, что для соблюдения хронологического порядка требуется очень строгий контроль за движением очереди, который дает возможность четко направлять клиентов к освобождающимся каналам обслуживания. В некоторых ситуациях решить эту проблему помогает присвоение клиентам номеров по мере их входа в систему. Многоканальная, многофазовая структура Эта ситуация в общем похожа на описанную в предыдущем разделе, с той лишь разницей, что в определенной последовательности выполняется две или несколько обслуживающих операций. Примером формата такого обслуживания может служить прием пациента в больнице, поскольку эта процедура обычно состоит из ряда этапов: первоначальный контакт с сотрудником приемного отделения, заполнение медицинских карт, получение идентификационных номерков, назначение палаты и отправка в нее пациента и т.д. Поскольку в этом процессе обычно задействовано несколько служащих, одновременно обслуживаются несколько пациентов. Комбинированная структура Этот тип структуры подразделяется на две категории: (1) структуры с переходом многоканального обслуживания в одноканальное и (2) структуры альтернативного пути. В первом случае разные очереди сливаются в одну для последующего однофазового обслуживания (как, например, при переходе через мост, когда две очереди объединяются в одну) либо они сливаются в одну очередь для многофазового обслуживания (например, когда комплектующие, поступающие с разных линий по сборке подузлов, поступают на основную сборочную линию). Во втором случае также возникают два варианта, отличающихся требованиями, предъявляемыми к упорядочению потока. Первый вариант напоминает многофазовую многоканальную структуру, но с возможностью перемещения клиентов из одного канала в другой после завершения первой обслуживающей операции. Во втором варианте количество фаз и каналов может варьироваться, но также после выполнения первой обслуживающей операции. Выход из системы После обслуживания клиента существует два сценария его выхода из системы: (1) он может вернуться в исходную генеральную совокупность и сразу стать вероятным кандидатом на следующее такое же обслуживание; (2) клиент не возвращается вообще либо вероятность повторного обслуживания его в данной системе очень мала. Для иллюстрации первой ситуации вспомним о станке, который только что отремонтировали после поломки и опять ввели в эксплуатацию, но в любой момент он может поломаться снова. Примером второй ситуации служит станок, который прошел капитальный ремонт или модернизирован и существует небольшая вероятность, что ему в ближайшем будущем снова понадобится такой же капитальный ремонт. Если говорить несерьезно, то первый случай можно назвать "рецидивным насморком", а второй "единовременной аппендэктомией" 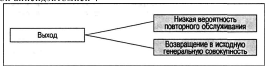 Очевидно, что если исходная генеральная совокупность является конечной, то любое поступление клиента (заявки) на обслуживание и последующий возврат его в исходную генеральную совокупность влечет за собой изменение параметров интенсивности входящего в сервисную систему потока. Это, разумеется, приводит к изменению характеристик анализируемой очереди и вызывает необходимость их уточнения. Модели очередей В этом разделе приведены примеры четырех типов задач анализа очередей с решениями. Все они имеют разную структуру, и для их решения применяются разные уравнения. Существуют и другие типы моделей, кроме этих четырех, но формулы для их решения слишком сложны, такие задачи обычно решаются с помощью компьютерного моделирования. Кроме того, при использовании представленных здесь формул следует помнить, что они получены при допущении, что анализируемый процесс в данный момент является устойчивым и неизменным. Следовательно, применение их к процессам, в которых интенсивности входящего потока и обслуживания изменяются во времени, может привести к неточным результатам. |
