Рро. методичка+к+решению+кр. Учебнометодическое пособие для выполнения расчетнографических работ и проведения практических занятий
 Скачать 2.03 Mb. Скачать 2.03 Mb.
|
Общая мощность лампP=P1+P2=60 + 40 = 100 Вт. Полученная энергия за 1 сут: W=Pt=10024=2400 Втч = 2,4 кВт.ч. Стоимость полученной энергии: с=W2,70=2,42,70=6,48 тенге. Пример 1.2 Для схемы (рисунок 1.2) заданы: внутреннее сопротивление источника Rвт=0,1 Ом и сопротивление проводов линии Rл=0,5 Ом. Определить КПД цепи, если напряжение приемника Ucd и сопротивление Rн те же, что и в примере 1.1. 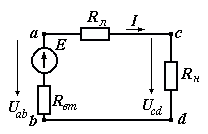 Рисунок 1.2 Решение. Очевидно, что мощность ламп Р1+Р2 и ток цепи I те же, что и в примере 1.1. Мощность потерь в линии RлI2 и во внутреннем сопротивлении источника RвтI2. Поэтому КПД: 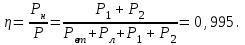 1.1 Методы расчета и свойства электрических цепей Постановка задачи. Общая задача анализа электрической цепи состоит в том, что в известной схеме цепи с заданными параметрами (ЭДС и сопротивлениями) необходимо рассчитать токи, мощности и напряжения на отдельных участках. Решение задач анализа. Решение задач анализа базируется на применении законов Ома и Кирхгофа. Закон Ома применяется главным образом при расчете режима отдельных участков цепи, а законы Кирхгофа при расчете режима более сложных электрических цепей. Решение задач с непосредственным применением законов Кирхгофа требует составления и решения значительного числа уравнений. В целях упрощения решений разработан ряд методов (например, контурных токов, узловых потенциалов), являющихся следствием применения уравнений Кирхгофа. Кроме того, применяются методы, базирующиеся на свойствах линейных электрических цепей: методы наложения, эквивалентного генератора и др. Далее рассматриваются наиболее распространенные методы. 1.1.1 Метод непосредственного применения закона Ома. Закон Ома применяется, как правило, для расчета значений электрических величин на отдельных пассивных и активных участках цепи. Пример 1.3 Для цепи (рисунок 1.3) заданы: E=100 В, Rвт=1 Ом, Rл=3 Ом, Rн=6 Ом. Требуется определить показания приборов. Решение. Ток в цепи (показание амперметра) определим из уравнения, составленного по второму закону Кирхгофа: I(Rвт+Rл+Rн)=E, 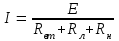 =10 А. =10 А.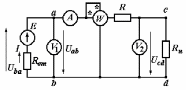 Рисунок 1.3 Применяя закон Ома для пассивного участка цепи, находим показания второго вольтметра: Ucd=IRн=60 В. По закону Ома для активного участка цепи найдем показания первого вольтметра: 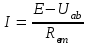 , , откуда Uab=EIRвт=10010=90 В. Ваттметр показывает мощность того участка цепи, к которому он подключен: P=UabI=900 Вт. Мощность Р - это мощность, отдаваемая источником во внешнюю цепь, или мощность потерь в линии (сопротивление Rл) и мощность приемника (сопротивление Рн). 1.1.2 Метод преобразования цепи. Метод состоит в том, что электрическая цепь или ее участки заменяются более простыми по структуре участками цепи, при этом токи и напряжения непреобразованной части цепи не должны измениться. В результате преобразования структура цепи и ее расчет упрощаются. Рассмотрим чаще всего встречающиеся преобразования. Преобразование последовательно соединенных резисторов или резистивных элементов. При последовательном соединении (рисунок 1.4,а) к одному из выводов предыдущего элемента присоединяется один из выводов последующего, так что после всех соединений получается участок с двумя выводами. Поэтому ток во всех последовательно соединенных элементах один и тот же.  Рисунок 1.4 Заменим последовательно соединенные элементы одним эквивалентным элементом с сопротивлением Rэ (рисунок 1.4,б). Напряжение U на выводах равно сумме падений напряжений на элементах: U=R1I+R2I+...+RnI=(R1+R2+...+Rn)I, а для схемы рис. 3.2, б напряжение U=RэI. По условиям эквивалентности при одном и том же напряжении U в схемах рисунков 1.4, a и б должен протекать один и тот же ток I. Поэтому RЭ=R1+R2+...+Rn, т.е. эквивалентное сопротивление последовательного соединения равно сумме сопротивлений последовательно соединенных резисторов или резистивных элементов. Преобразование параллельно соединенных резисторов или резистивных элементов. Оно (рисунок 1.5,а) характеризуется тем, что все элементы присоединяются к одной и той же паре узлов. При этом ко всем элементам приложено одно и то же напряжение U. Для схемы (рисунок 1.5,а) на основании первого закона Кирхгофа можно записать: I=I1+I2+...+In, или, учитывая, что для каждой ветви по закону Ома 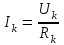 , ,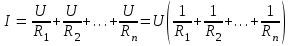 . .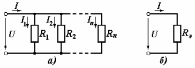 Рисунок 1.5 Заменим параллельно соединенные элементы одним эквивалентным элементом с сопротивлением RЭ, (рисунок 1.5,б). Для этой схемы ток 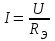 . По условиям эквивалентности при том же напряжении U в схемах рисунки 1.5, а и б токи должны быть одинаковыми. Поэтому . По условиям эквивалентности при том же напряжении U в схемах рисунки 1.5, а и б токи должны быть одинаковыми. Поэтому 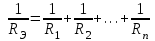 , ,и для проводимостей GЭ =G1+G2+...+Gn. т.е. эквивалентная проводимость параллельно соединенных резистивных элементов равна сумме их проводимостей. В частном случае, если параллельно соединены два резистора, их эквивалентная проводимость GЭ=G1+G2 или 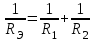 , а эквивалентное сопротивление , а эквивалентное сопротивление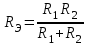 . .Преобразование схемы при смешанном соединении резисторов или резистивных элементов. Оно представляет собой комбинацию последовательного и параллельного соединений. Эквивалентное сопротивление находится путем постепенного упрощения схемы и «свертывания» ее, так чтобы получить одно сопротивление. При расчете токов в отдельных ветвях схему «развертывают» в обратном порядке. Поясним сказанное на примере. Пример 1.4 Для цепи (рисунок 1.6) найти эквивалентное сопротивление, токи в неразветвленной части цепи и в отдельных ветвях. К цепи приложено напряжение U. 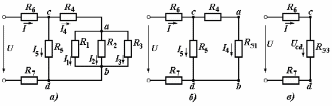 Рисунок 1.6 Решение. Сопротивления R1, R2, R3 соединены параллельно. Их, эквивалентная проводимость GЭ1 и сопротивление RЭ1 равны: Gэ1=G1+G1+G3= 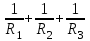 ; ; 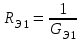 . .В результате схема (рисунок 1.6,а) приводится к эквивалентной схеме (рисунок 1.6,б), у которой сопротивления R4 и RЭ1 соединены последовательно. Их эквивалентное сопротивление RЭ2=R4+RЭ1. На участке cd сопротивления R5 и RЭ2 соединены параллельно. Их эквивалентное сопротивление 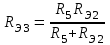 . Схема (рисунок 1.6,б), таким образом, приводится к схеме (рисунок 1.6,в), у которой сопротивления R6, RЭ3, R7 соединены последовательно. Эквивалентное сопротивление цепи RЭ=R6+RЭ3+R7. . Схема (рисунок 1.6,б), таким образом, приводится к схеме (рисунок 1.6,в), у которой сопротивления R6, RЭ3, R7 соединены последовательно. Эквивалентное сопротивление цепи RЭ=R6+RЭ3+R7.Ток в неразветвленной части цепи 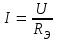 . Для расчета токов в ветвях определим напряжение на разветвленном участке цепи Ucd. По закону Ома для пассивного участка цепи Ucd=IRЭ3. Токи в ветвях . Для расчета токов в ветвях определим напряжение на разветвленном участке цепи Ucd. По закону Ома для пассивного участка цепи Ucd=IRЭ3. Токи в ветвях 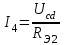 и и 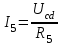 . Напряжение Uab=RЭ1I4. Токи в ветвях: . Напряжение Uab=RЭ1I4. Токи в ветвях: 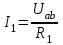 , , 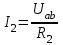 , , 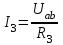 . . 1.1.3 Взаимные преобразования звезды и треугольника сопротивлений. В сложных цепях встречаются соединения, которые нельзя отнести ни к последовательным, ни к параллельным соединениям. К таким соединениям относятся трехлучевая звезда (рисунок 1.7, а) и треугольник (рисунок 1.7,б) сопротивлений. 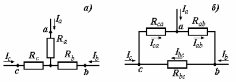 |
