Рро. методичка+к+решению+кр. Учебнометодическое пособие для выполнения расчетнографических работ и проведения практических занятий
 Скачать 2.03 Mb. Скачать 2.03 Mb.
|
|
2.3 Основные элементы цепи синусоидального тока Примечание. Для цепей переменного синусоидального тока справедливы законы Ома, Кирхгофа и все методы расчета, рассмотренные нами для цепей постоянного тока, с той разницей, что во всех законах и уравнениях должны быть использованы либо мгновенные значения параметров, либо комплексные действующие значения. Цепь синусоидального тока может содержать три основных идеальных элемента: резистор (резистивный элемент), катушка индуктивности (индуктивный элемент) и конденсатор (емкостной элемент). При относительно невысоких частотах сопротивление резистивного элемента R не зависит от частоты питающего напряжения, а индуктивное и емкостное сопротивления зависят от частоты. Если к отдельному элементу приложено синусоидальное напряжение u=Umsin(t+u), то ток: для резистора 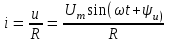 или или 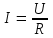 или или 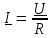 ; ;для катушки индуктивности 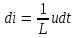 , ,продифференцировав это выражение получим 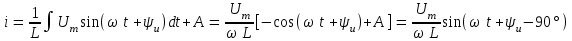 или 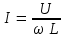 или или 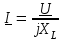 , ,где XL=L индуктивное сопротивление катушки; для конденсатора 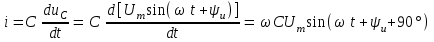 или I=CU или 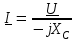 , ,где 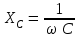 емкостное сопротивление конденсатора. емкостное сопротивление конденсатора.Пример 2.4 К резистору с сопротивлением R=10 Ом приложено синусоидальное напряжение u=310sin(t+30) В. Найти показания амперметра, изменяющего действующее значение, и записать мгновенное значение тока. Решение. Действующее значение напряжения 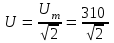 220 В. 220 В.Комплексное напряжение 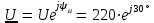 В. В.По закону Ома комплексное действующее значение тока 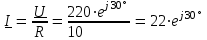 А. А.Показания амперметра равны модулю комплексного действующего значения тока, т.е. амперметр покажет 22 А. Мгновенное значение тока можно записать, так как известны его амплитуда и начальная фаза: i=Imsin(t+i)=22 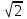 sin(t+30) А. sin(t+30) А.На рисунке 2.5 приведены схема подключения резистора, графики мгновенных значений напряжения и тока, а также векторная диаграмма. 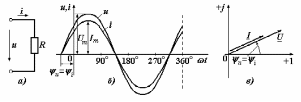 Рисунок 2.5 Пример 2.5 К индуктивному элементу =100 мГн приложено синусоидальное напряжение u=310sin(314t+45)В. Найти действующее значение тока, записать его мгновенное значение и мгновенное значение ЭДС самоиндукции. Построить на комплексной плоскости векторы 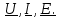 Решение. Действующее значение напряжения 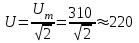 В. В.На рисунке 2.6 приведены схема подключения катушки индуктивности, графики мгновенных значений напряжения и тока, а также векторная диаграмма для общего случая. 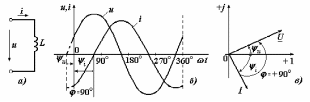 Рисунок 2.6 Комплексное напряжение 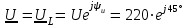 В. В.Индуктивное сопротивление XL=L=314100103=31,4 Ом. Индуктивное сопротивление в комплексной форме jXL=j31,4 Ом. Ток в индуктивном элементе 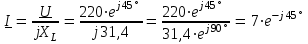 А. А.Его мгновенное значение i= 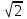 Isin(t+i)=7 Isin(t+i)=7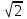 sin(314t45) А. sin(314t45) А.Мгновенное значение ЭДС самоиндукции eL=u=Umsin(t+45+180)=310sin(314t+225) В. или в комплексной форме: 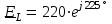 В. В.Векторная диаграмма изображена на рисунке 2.7. 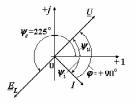 Рисунок 2.7 Пример 2.6 К сети с синусоидальным напряжением частотой 50 Гц подключен емкостной элемент С (рисунок 2.8). Приборы для измерения действующих значений показывают: вольтметр 220 В, амперметр 2 А. Определить емкость С. 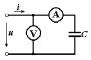 Рисунок 2.8 Решение. На рисунке 2.9 приведены схема подключения катушки индуктивности, графики мгновенных значений напряжения и тока, а также векторная диаграмма. Так как частота известна, то для определения емкости С достаточно определить емкостное сопротивление ХС по закону Ома для участка цепи с емкостью. 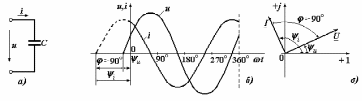 Рисунок 2.9 Из 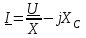 для модулей находим: для модулей находим: 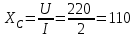 Ом. Ом.Емкость 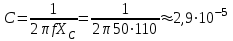 Ф=29 мкФ. Ф=29 мкФ.2.4 Цепь синусоидального тока при последовательном соединении элементов 2.4.1 Закон Ома для участка цепи с последовательным соединением элементов R, L, C (рисунок 2.10). Если к такому участку цепи приложено напряжение u=Umsin(t+u), то ток в цепи синусоидальный: i=Imsin(t+i). По второму закону Кирхгофа для комплексных действующих значений, получим: 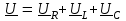 Ранее было получено 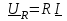 ; ; 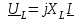 ; ; 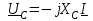 . .Поэтому 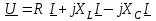 . .Запишем закон Ома в комплексной форме 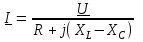 . .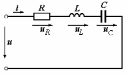 Рисунок 2.10 2.4.2. Комплексное и полное сопротивление цепи синусоидального тока. Знаменатель выше полученного выражения обозначим 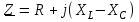 и назовем его комплексным сопротивлением, а X=XLXС реактивным сопротивлением. Представим комплексное сопротивление в показательной форме: 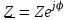 , ,где 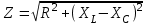 модуль комплексного сопротивления или полное сопротивление цепи; модуль комплексного сопротивления или полное сопротивление цепи;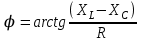 аргумент комплексного сопротивления. аргумент комплексного сопротивления.Итак 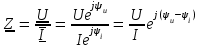 или или 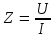 , , 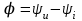 . .Пример 2.7 В цепь синусоидального тока последовательно включены элементы с сопротивлениями R=8 Ом, XL=4 Ом, XС=10 Ом (рисунок 2.10). Определить ток в цепи, напряжение на отдельных участках и угол сдвига фаз между общим напряжением и током, если действующее значение напряжения, приложенного к цепи, U=220 В. Построить векторную диаграмму. Решение. Комплексное сопротивление цепи 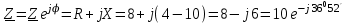 Ом. Ом.Ток в цепи 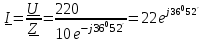 A. A.(начальная фаза напряжения u принята равной нулю). Напряжение на элементах 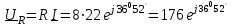 В; В;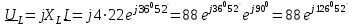 В; В;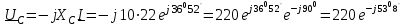 В. В.Угол сдвига фаз между напряжением и током =ui=03652'=3652'. Векторная диаграмма представлена на рисунке 2.11. Для ее построения выбраны масштабы напряжения и тока. 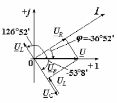 Рисунок 2.11 Пример 2.8 В сеть синусоидального напряжения частотой 50 Гц включена катушка индуктивности с параметрами L, R (рисунок 2.12). Приборы, измеряющие действующие значения напряжения и тока, включенные в цепь, показывают: U=220 В, I=25 А. Активное сопротивление катушки R=4,4 Ом. Определить индуктивность катушки, угол сдвига фаз между напряжением и током, построить векторную диаграмму. 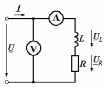 Рисунок 2.12 Решение. Полное сопротивление катушки 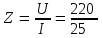 =8,8 Ом. =8,8 Ом.Из формул 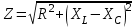 и и 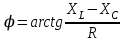 при XC=0 следует, что при XC=0 следует, что 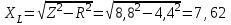 Ом; Ом; 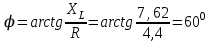 . .Так как частота сети f=50 Гц, то 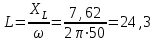 мГн. Напряжения: мГн. Напряжения:UR=RI=4,4·25=110 B; UL=XLI=7,62·25=190,5 B. Для построения векторной диаграммы выберем равной нулю начальную фазу тока. Построим в выбранном масштабе mI вектор тока. Вектор 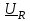 совпадает по фазе с вектором совпадает по фазе с вектором 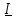 , а вектор , а вектор 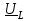 опережает его по фазе на угол 90. Вектор напряжения сети опережает его по фазе на угол 90. Вектор напряжения сети 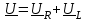 (рисунок 2.13). При построении векторов напряжений выбран масштаб mU. (рисунок 2.13). При построении векторов напряжений выбран масштаб mU.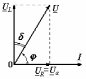 Рисунок 2.13 Пример 2.9 В сеть с частотой 100 Гц включены резистор с сопротивлением R=12 Ом и конденсатор емкостью С=9950 мкФ (рисунок 2.14). Определить мгновенное значение напряжения сети, построить векторную диаграмму, если действующее значение тока I=5 А. 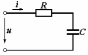 Рисунок 2.14 Решение. Из формулы 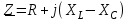 (при XL=0) находим комплексное сопротивление цепи (при XL=0) находим комплексное сопротивление цепи 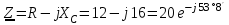 Ом. Ом.Напряжение сети 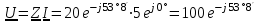 В (начальная фаза тока і принята равной нулю). Переходя от комплексного выражения к мгновенному значению, получаем: u=Umsin(t+u)=100 В (начальная фаза тока і принята равной нулю). Переходя от комплексного выражения к мгновенному значению, получаем: u=Umsin(t+u)=100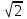 sin(t538) В. sin(t538) В.Для построения векторной диаграммы выбираем масштабы mU и mI. Строим векторы напряжений в соответствии с расчетом (рисунок 2.15): 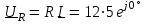 =60 В; =60 В;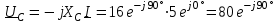 В. В.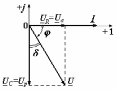 Рисунок 2.15 Угол сдвига фаз равен аргументу комплексного сопротивления, т.е. =538. 2.5 Проводимость цепи синусоидального тока В цепях синусоидального тока, как и в цепях постоянного тока, вводится понятие проводимости. Под комплексной проводимостью Y понимают отношение комплексного действующего тока к комплексному действующему значению напряжения (или комплексных амплитуд) 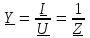 или или 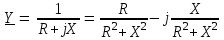 . .Действительную часть комплексной проводимости обозначают 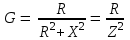 и называют активной проводимостью. Мнимую часть обозначают 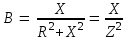 и называют реактивной проводимостью. Так как реактивное сопротивление X=XLXC, то 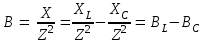 , ,где 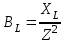 индуктивная проводимость; индуктивная проводимость; 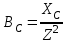 емкостная проводимость. емкостная проводимость.С учетом принятых обозначений можно записать 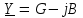 или или 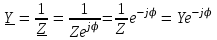 , ,где 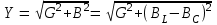 модуль или полная проводимость; модуль или полная проводимость;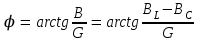 аргумент проводимости. аргумент проводимости.2.6 Параллельное соединение ветвей Рассмотрим в качестве примера цепь с двумя параллельными ветвями, параметры которых R1, L и R2, C (рисунок 2.16). 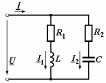 Рисунок 2.16 Из первого закона Кирхгофа следует, что 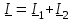 где 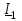 , , 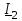 токи в параллельных ветвях; токи в параллельных ветвях; 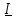 общий ток. общий ток.Запишем выражение для каждого тока по закону Ома 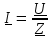 ; ; 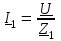 ; ; 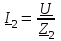 и получим 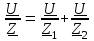 или или 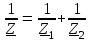 или или 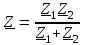 . .Учитывая, что 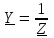 , получаем выражение для комплексной проводимости: , получаем выражение для комплексной проводимости: 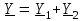 . .Представим 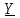 , , 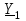 , , 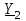 в алгебраической форме: в алгебраической форме:GjB=G1jBL+G2+jBC=(G1+G2)j(BLBC) Приравняв действительные и мнимые части, получим: G =G1+G2; B=BLBC. Представим 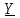 в показательной форме: в показательной форме: 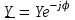 , , где 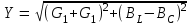 полная проводимость: полная проводимость: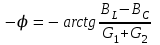 - аргумент проводимости. - аргумент проводимости.Для построения векторной диаграммы разложим векторы токов на две составляющие: совпадающие по направлению с вектором 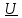 и перпендикулярные ему. Эти составляющие токов назовем соответственно активной и перпендикулярные ему. Эти составляющие токов назовем соответственно активной 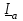 и реактивной и реактивной 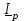 составляющими. Векторная диаграмма представлена на рисунке 2.17. составляющими. Векторная диаграмма представлена на рисунке 2.17.Из векторной диаграммы следует, что 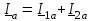 ; ; 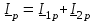 ; ; 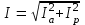 . .Как видно из векторной диаграммы, реактивная составляющая тока в активно-индуктивной ветви отстает по фазе от напряжения на угол 90°, а реактивная составляющая тока в активно-емкостной ветви опережает напряжение на угол 90°. 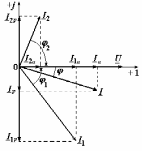 Рисунок 2.17 Из векторной диаграммы также следует, что Ia=Icos; Ip=Isin. Так как 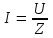 , , 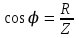 , , 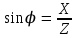 , то , то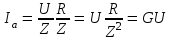 ; ; 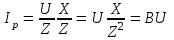 , ,т.е. активную и реактивную составляющие тока можно получить, умножая напряжение на соответствующие проводимости. Пример 2.10 Заданы параметры цепи с двумя параллельными ветвями (рисунок 2.18): R1=10 Ом, R2=8 Ом, XС=6 Ом. Напряжение питания U=127 В. Определить токи в ветвях и общий ток. Построить векторную диаграмму, на которой показать активную и реактивную составляющие общего тока. 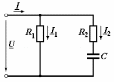 Рисунок 2.18 Решение. Начальную фазу напряжения примем равной нулю (u=0), т.е. 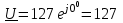 В. Комплексные сопротивления ветвей: В. Комплексные сопротивления ветвей: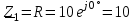 Ом; Ом; 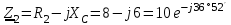 Ом. Ом.Токи в ветвях 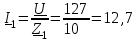 А; А;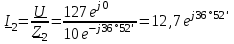 А. А.Общий ток 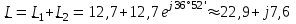 А. А.Для построения векторной диаграммы выберем масштаб для напряжения и тока. Проведем оси комплексной плоскости и построим векторы напряжения и токов в выбранном масштабе (рисунок 2.19). Активную и реактивную составляющие общего тока найдем разложением вектора тока на две составляющие, одна из которых совпадает по направлению с вектором напряжения, а другая перпендикулярна ему: Iа =Icos; Iр =Isin . 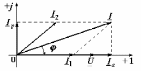 Рисунок 2.19 Пример 2.11 В цепи синусоидального тока частотой 50 Гц включены параллельно катушка и конденсатор (рисунок 2.20). Измерительные приборы показывают действующие значения напряжения и токов: U=40 B; I=0,13 A, I1=0,18 A, I2=0,115 A. Активное сопротивление катушки R=90 Ом. Определить сопротивления ветвей и их общее сопротивление, полную, активную и реактивную проводимости, углы сдвига фаз в двух ветвях и между напряжением и общим током, индуктивность катушки L и емкость конденсатора C. Построить векторную диаграмму. Решение. Начальную фазу напряжения примем равной нулю, то есть 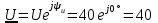 В. В.Полное сопротивление катушки 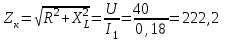 Ом. Ом.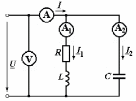 Рисунок 2.20 Индуктивное сопротивление 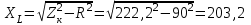 Ом; Ом;Угол сдвига фаз в катушке 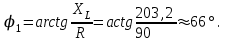 Комплексное сопротивление катушки 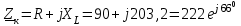 Ом. Ом.Полное сопротивление конденсатора равно его емкостному сопротивлению 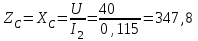 Ом. Ом.Комплексное сопротивление конденсатора 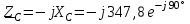 Ом. Ом.то есть 2=900. Комплексное сопротивление двух ветвей 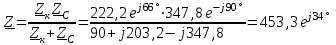 Ом. Ом.Комплексная проводимость двух ветвей 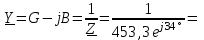 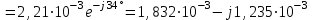 См. См.то есть активная проводимость G=1,83210–3 Cм, реактивная проводимость В=+1,23510–3 См; следовательно, у параллельного соединения активно-индуктивное сопротивление (проводимость). Общий ток 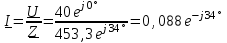 А. А. |
