Рро. методичка+к+решению+кр. Учебнометодическое пособие для выполнения расчетнографических работ и проведения практических занятий

• Название: Учебнометодическое пособие для выполнения расчетнографических работ и проведения практических занятий
• Дата: 27.12.2022
• Размер: 2.03 Mb.
• Имя файла: методичка+к+решению+кр.docx
• Тип: Учебно-методическое пособие; #866630
• страница: 4 из 11

Рисунок 1.9

При параллельном соединении ветвей с источниками ЭДС и сопротивлениями (рисунок 1.10, а) общий ток I равен при указанных положительных направлениях сумме токов в ветвях:

I=I₁+I₂+...+I_n.

Токи в ветвях по обобщенному закону Ома соответст­венно равны:

I₁=(U_ba+E₁)G₁; I₂=(U_ba–E₂)G₂; ... I_n=(U_ba+E_n)G_n.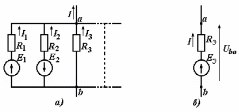



Рисунок 1.10

Подставляя значения токов, получаем:

I=G₁E₁+G₁U_baG₂E₂+G₂U_ba+...+G_nE_n+G_nU_ba=G₁E₁

G₂E₂+...+G_nE_n+(G₁+G₂+...+G_n)U_ba=

=G_kE_k + U_baG_k

Для эквивалентной схемы (рисунок 1.10,б)

I=G_Э(U_ba+E_Э)=G_ЭE_Э+G_ЭU_ba

Сравнивая выражения для тока I в схемах на рисунках 1.10, а и б, имеем:

G_k=G_э; G_kE_k=G_эE_э,

откуда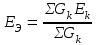

.

Эквивалентная ЭДС при параллельном соединении вет­вей равна алгебраической сумме произведений ЭДС ветви на проводимость ветви, деленную на сумму проводимостей ветвей.

Если в какой-либо ветви ЭДС направлена противопо­ложно выбранному направлению эквивалентной ЭДС Е_Э,то произведение G_kE_k записывается со знаком минус. Ес­ли в ветви ЭДС отсутствует, то соответствующее слагаемое G_kE_k тоже отсутствует.

Пример 1.6 Заменить часть цепи (рисунок 1.11) эквивалентной схемой по рисунку 1.10,б.

Решение.

Эквивалентная проводимость G_э=G₁+G₂+G₃. Эквивалентная ЭДС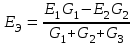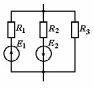

.



Рисунок 1.11

1.1.5 Метод непосредственного применения законов Кирхгофа. Законы Кирхгофа наиболее общие, универсальные законы, описывающие режим элект­рической цепи, и методы расчета, основанные на этих законах, применимы к расчету режима любой электричес­кой цепи. Однако в практике расчетов их чаще всего при­меняют для определения токов в ветвях сложных цепей с несколькими источниками электрической энергии.

Порядок расчета. При расчете рекомендуется оп­ределенная последовательность решения, которая далее иллюстрируется на примере расчета токов в схеме (рисунок 1.12) при заданных сопротивлениях и ЭДС.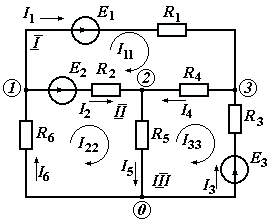



Рисунок 1.12

1) Определяется число ветвей, т.е. число неизвестных токов, и узлов, которые обозначаются буквами или цифра­ми (1, 2, 3, 0 на рисунке 1.12); выбираются произвольно и ука­зываются положительные направления токов.

2) Определяется, сколько уравнений нужно составить по первому закону Кирхгофа и сколько по второму. Общее число уравнений должно быть равно числу неизвестных то­ков, т.е. числу ветвей n. По первому закону составляется у1 уравнений, где у - число узлов схемы (уравнение для одного из узлов является следствием остальных, т.е. не является независимым; оно может быть получено сумми­рованием всех остальных у1 уравнений). Число уравне­ний, которые требуется составить по второму закону Кирх­гофа, меньше общего числа уравнений на число уравне­ний, составленных по первому закону Кирхгофа, т.е. по второму закону Кирхгофа нужно составить n(у1) независимых уравнений.

Для схемы на рисунке 1.12 число ветвей n=6, число узлов y=4. По первому закону Кирхгофа необходимо составить 41=3 уравнения, а по второму 6(41)=3 уравнения.

3) Составляются уравнения. При составлении у1 урав­нений по первому закону Кирхгофа токам, направленным от узла, приписывается знак плюс, а направленным к уз­лу,  знак минус (или наоборот). Уравнения по второму закону составляются для контуров, так, чтобы в каждый следующий контур входила хотя бы одна ветвь, не вошед­шая в другие контуры, для которых уже записаны уравне­ния. Выбирается направление обхода каждого конту­ра (произвольно). При обходе контура в выбранном на­правлении ЭДС записывается со знаком плюс, если ее на­правление совпадает с направлением обхода контура, и со знаком минус в противном случае; падение напряжения RI записывается со знаком плюс, если направление обхо­да ветви совпадает с положительным направлением тока, и со знаком минус в противном случае.

Для схемы составим три уравнения по перво­му закону Кирхгофа для узлов 1, 2, 3:

I₁ + I₂  I₆ = 0 - узел 1.

 I₂  I₄ + I₅ = 0 - узел 2.

 I₁ + I₄  I₃ = 0 - узел 3.

По второму закону Кирхгофа составим три уравнения (направление обхода контуров примем по направлению движения часовой стрелки):

R₁I₁ + R₄I₄  R₂I₂ = E₁  E₂ -контур I;

R₂I₂ + R₅I₅ + R₆I₆ = E₂ -контур II;

 R₃I₃  R₅I₅  R₄I₄ =  E₃ -контур III.

Решив уравнения совместно, найдем искомые токи. Ес­ли численное значение какого-либо тока получается отри­цательным, то это означает, что его действительное на­правление противоположно выбранному положительному (в этих случаях изменять принятое направление тока не рекомендуется).

Пример 1.7 Дана схема (рисунок 1.13). ЭДС E₁=110 В, E₃=111 В, E₄=108 В, внутренние сопротивления источников R_вт1=0,5 Ом, R_вт3=1 Ом, R_вт4=0,2 Ом, сопротивления R₁=4,5 Ом, R₂=20 Ом, R₄=25,8 Ом. Определить токи в ветвях.

Решение.

1) Между точками а' и а" нет включенного сопротив­ления или ЭДС, следовательно, их потенциалы одинаковы и их можно объединить в общий узел. Аналогично объединяются точки b и b". Следовательно, схема имеет два узла, между которыми включены че­тыре ветви и число неизвестных токов равно четырем. Выбранные по­ложительные направления токов показаны на схеме.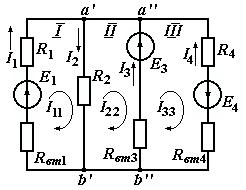



Рисунок 1.13

2) Схема имеет два узла и четыре ветви, поэтому по первому зако­ну Кирхгофа надо составить у1=21=1 уравнение, а по второму n(у 1)=41=3 уравнения.

3) Составим одно уравнение по первому закону для узла а:

 I₁ + I₂  I₃  I₄ =0

и три по второму, принимая направление обхода контуров по направлению движения часовой стрелки:

(R_вт1 + R₁)I₁ + R₂I₂ = E₁ - контур I;

R₂I₂  R_вт3I₃ =  E₃ - контур II;

R_вт3I₃  (R_вт4 + R₄)I₁ = E₃ + E₄ - контур III.
В полученную систему уравнений подставим численные значения ЭДС и сопротивлений:

Решим систему уравнений методом подстановки. Откуда I₁ =2 А; затем найдем I₂ = 5 А, I₃ =11 А, I₄ =  8 А.
1.1.6 Метод контурных токов. Это широко распростра­ненный метод расчета сложных электрических цепей с не­сколькими контурами и несколькими источниками элект­рической энергии. В основе метода лежат законы Кирхго­фа и два предположения: в каждом контуре протекают независимые друг от друга расчетные токи, называемые контурными, а ток каждой ветви равен алгебраической сумме контурных токов, замыкающихся через эту ветвь.

При этих предположениях оказывается, что для расче­та схемы достаточно ограничиться составлением уравнений для контурных токов только по второму закону Кирхгофа, так как для контурных токов первый закон выполняется в силу принятых для контурных токов предположений (контурный ток в одной из ветвей контура направлен к узлу, а в другой  от узла).

Следовательно, вместо в урав­нений при непосредственном применении законов Кирхго­фа достаточно составить n(у1) уравнений, что значи­тельно упрощает расчет.

Пример расчета. Поясним метод на примере схе­мы рисунок 1.12. Выше для этой схемы было получено, что в(у1)=3. Выделим в схеме три независимых контура (I, II, III) с контурными токами I₁₁, I₂₂, I₃₃. Направление контурных токов можно выбрать произвольно, но для еди­нообразия последующих формул и расчетов следует (если возможно) задавать контурным

токам направления, совпа­дающие с направлениями обхода контуров (в данном слу­чае с направлением движения часовой стрелки).

Для контурных токов составим уравнения по второму закону Кирхгофа:

(R₁+R₂+R₃)I₁₁R₂I₂₂R₄I₃₃=E₁E₂  контур I;

R₂I₁₁+(R₂+ R₅+ R₆) I₂₂R₅I₃₃=E₂  контур II;

R₄I₁₁R₅ I₂₂+(R₃+ R₄+ R₅) I₃₃=E₃  контур III.

Так как направление обхода контура совпадает с направлением тока в этом контуре, то падения напряжения i от этого тока запишем со знаком плюс. В общих ветвях ток смежного контура направлен противоположно току контура, поэтому падение напряжения от тока смежного контура запишем со знаком минус.

Решив уравнения совместно, определим ; контурные токи I₁₁, I₂₂, I₃₃. Токи ветвей равны алгебраиче­ским суммам контурных токов. При этом знаки у контурных токов определяем по следующему правилу: если на­правление контурного тока совпадает с направлением тока ветви, то он записывается со знаком плюс, если не совпадает  со знаком минус.

Токи ветвей:

I₁=I₁₁; I₂=I₁₁+I₂₂; I₃=I₃₃; I₄=I₁₁I₃₃; I₅=I₂₂I₃₃; I₆=I₂₂.
Пример 1.8 Решить пример 1.7 методом контурных токов.

Решение.

Выберем независимые контуры (рисунок 1.13)  внутренние контуры (ячейки) схемы, положительные направления контурных токов I₁₁, I₂₂, I₃₃ примем совпадающими с направлением обхода контуров. Составим уравнения по второму закону Кирхгофа для контурных токов: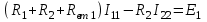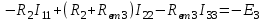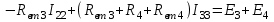

;

;

.
Подставив заданные численные значения, получим: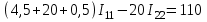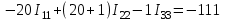

;

;