Рро. методичка+к+решению+кр. Учебнометодическое пособие для выполнения расчетнографических работ и проведения практических занятий
 Скачать 2.03 Mb. Скачать 2.03 Mb.
|
Угол сдвига фаз между напряжением и общим током=u-i=0–(34)=34 (равен аргументу 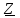 ). ).Индуктивность катушки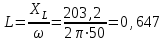 Гн. Гн.Емкость конденсатора 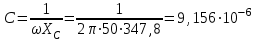 Ф. Ф.Выбрав масштабы для напряжения mu и тока mI , построение векторной диаграммы начнем с вектора 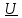 (рисунок 2.42). Ток (рисунок 2.42). Ток 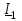 отстает по фазе от напряжения отстает по фазе от напряжения 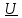 на угол 2=90. Общий ток на угол 2=90. Общий ток 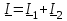 отстает по фазе от напряжения на угол =+34. отстает по фазе от напряжения на угол =+34.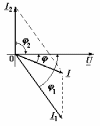 Рисунок 2.21 Пример 2.12 Параллельно соединены три элемента с сопротивлениями: R=10 Ом, XL=20 Ом, ХС= 10 Ом (рисунок 2.22). Общее напряжение U=100 В. Определить токи в элементах, общий ток и его угол сдвига фаз относительно напряжения. Построить векторную диаграмму. 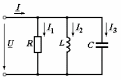 Рисунок 2.22 Решение. Найдем комплексные проводимости ветвей: 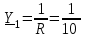 См; См;  См; См; 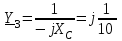 См. См.Комплексная проводимость параллельного соединения 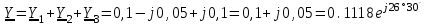 См. См.Токи: 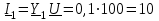 А; А; 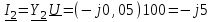 А; А;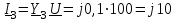 А; А; 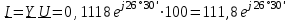 А. А.Угол сдвига фаз =u-i =02630=–2630. Векторная диаграмма изображена на рисунке 2.23. 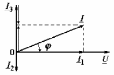 Рисунок 2.23 Пример 2.13 Для цепи (рисунок 2.24) заданны сопротивления элементов: R1=15 Ом; R2=8 Ом; R3=6 Ом; R4=4 Ом; XL1=10 Ом; XC2=6 Ом; XL3=8 Ом. Мгновенное значение напряжения на входе цепи u=141sin314t В. Определить показания амперметров, построить векторную диаграмму токов и топографическую диаграмму напряжений. Решение. Вычислим комплексные сопротивления всех ветвей: 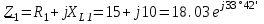 Ом; Ом;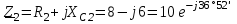 Ом; Ом;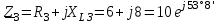 Ом; Ом;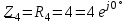 Ом. Ом.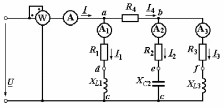 Рисунок 2.24 Общее комплексное сопротивление второй и третьей ветвей 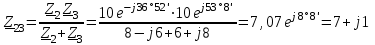 Ом. Ом.Общее комплексное сопротивление второй, третьей и четвертой ветвей 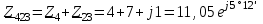 Ом. Ом.Сопротивления 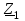 и и 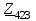 соединены параллельно (между точками а и с или входными выводами). Поэтому комплексное сопротивление всей цепи соединены параллельно (между точками а и с или входными выводами). Поэтому комплексное сопротивление всей цепи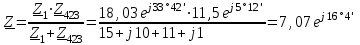 Ом. Ом.Комплексное действующее значение напряжения 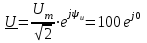 В. В.Ток в неразветвленной части цепи 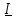 , токи , токи 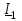 , , 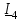 найдем по закону Ома в комплексной форме: найдем по закону Ома в комплексной форме: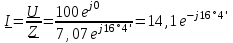 А; А;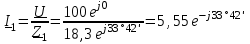 А; А;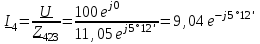 А. А.Напряжение между точками b и c, т.е. на выводах параллельных ветвей, 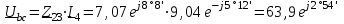 В. В.Токи 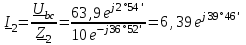 А; А;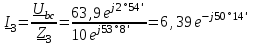 А. А.Амперметр показывает действующее значение тока (если в задаче нет специальных указаний), которое равно модулю комплексного тока. Таким образом, показания амперметров: А1=5,55 А; А2=6,39 А; А3=6,39 А; А=14,1 А. Для построения векторной и топографической диаграмм выберем масштабы напряжения и тока: mu, mi, проведем оси комплексной плоскости. Потенциал точки с примем равным нулю. В соответствии с расчетом построим на комплексной плоскости токи 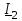 , , 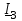 , , 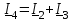 , затем , затем 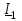 и и 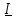 . Рассчитаем комплексные потенциалы точек, указанных на рисунке 2.24. . Рассчитаем комплексные потенциалы точек, указанных на рисунке 2.24.Комплексные потенциалы точек d, e и f будут: 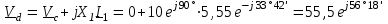 В; В;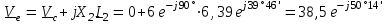 В; В;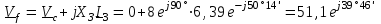 В. В.Потенциал точки b 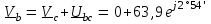 В. В.Потенциал точки a 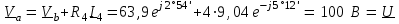 , ,как и должно быть. Отложив на комплексной плоскости (рисунок 2.25) векторы, соответствующие комплексным потенциалам, получим на диаграмме точки a, b, d, e, f. Соединяющие их векторы равны соответствующим комплексным напряжениям. 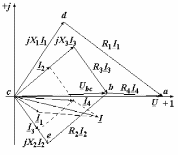 Рисунок 2.25 2.7 Методы расчета цепей синусоидального тока Все методы расчета цепей постоянного тока применимы в комплексной форме к расчету цепей синусоидального тока. Проиллюстрируем различные методы расчета на примере достаточно простой цепи, изображенной на рисунке 2.26. ЭДС источника 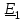 =100 В, =100 В, 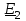 =j100 В, комплексные сопротивления =j100 В, комплексные сопротивления 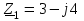 ; ; 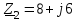 ; ; 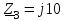 . Требуется определить токи в ветвях различными методами. . Требуется определить токи в ветвях различными методами.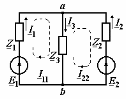 Рисунок 2.26 2.7.1 Метод непосредственного применения законов Кирхгофа. Цепь состоит из трех ветвей, поэтому требуется составить три уравнения, выбрав положительные направления токов в ветвях, одно по первому закону Кирхгофа 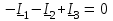 и два по второму закону Кирхгофа  ; ; 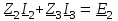 . .Подставив заданные величины, получим три уравнения с тремя неизвестными: 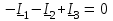 ; ; 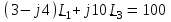 ; ; 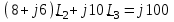 . .Решив уравнения совместно, определим искомые токи: 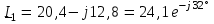 А; А; 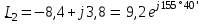 А; А;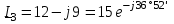 А. А.2.7.2 Метод контурных токов. Для внутренних контуров (ячеек) составим уравнения по второму закону Кирхгофа для контурных токов: 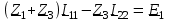 ; ; 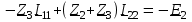 . .Подставив в уравнения численные значения, получим два уравнения с двумя неизвестными контурными токами: 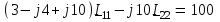 ; ;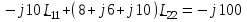 . .Решив уравнения совместно, определим значения контурных токов и токов в ветвях: 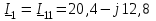 А; А; 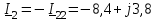 А; А;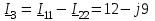 А. А.2.7.3 Метод двух узлов. Напряжение между узлами а и b определим по формуле для узловых потенциалов, но при комплексных значениях всех величин: 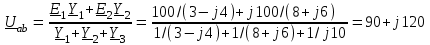 В. В.Токи в ветвях найдем по закону Ома: 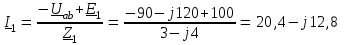 А; А;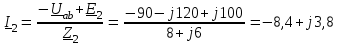 А; А;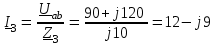 А. А.2.7.4 Метод наложения. Для заданной цепи построим две вспомогательные схемы с одним источником ЭДС в каждой (рисунок 2.27, а, б). Рассчитаем токи во вспомогательных схемах при выбранных положительных направлениях. а) Для схемы на рисунке 2.27,а: 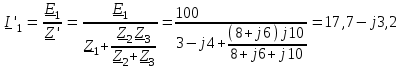 А; А;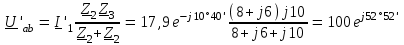 В; В;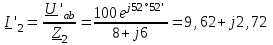 А; А;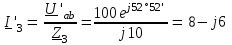 А. А.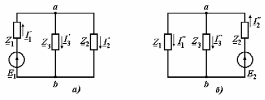 Рисунок 2.27 б) Для схемы на рисунке 2.27,б: 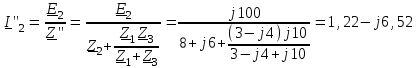 А; А;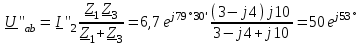 В; В;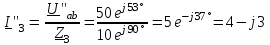 А; А;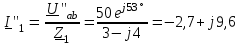 А. А.Токи в заданной цепи равны алгебраическим суммам токов вспомогательных схем: 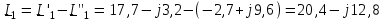 А; А;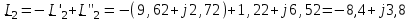 А; А;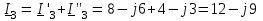 А. А.2.8 Мощность цепи синусоидального тока 2.8.1 Активная мощность. Мощность необратимых преобразований энергии на участке цепи за период: 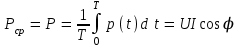 . .Средняя за период мощность зависит от угла сдвига фаз между напряжением и током и не равна нулю, если участок цепи имеет активное сопротивление. Из основной формулы активной мощности можно получить производные формулы для участков цепи с сопротивлением Z: P=UIcos=UaI=I2Zcos=RI2=GU2. 2.8.2 Реактивная мощность. Мощность реактивных элементов рр=pL+pC в среднем за период равна нулю, но в течение четверти периода она положительна, что физически означает накопление энергии в магнитном поле катушки или в электрическом поле конденсатора, а в течение следующей четверти периода отрицательная, что соответствует обратному процессу. Таким образом, имеет место процесс колебания энергии, но необратимых преобразований энергии нет. Мощность колеблющейся энергии в отличие от активной называют реактивной и обозначают буквой Q: Q=UIsin. Единицу реактивной мощности называют вольт-ампер реактивный – вар. Для индуктивного элемента реактивная мощность Q=UI=QL, так как sin=sin90=1. Для емкостного элемента реактивная мощность Q=–UI=–QС, так как sin=sin(90)=1. Если индуктивный и емкостный элементы соединены последовательно, то Q=QL– QС. Из основной формулы реактивной мощности легко получить производные формулы: Q=UIsin=UpI=I2Zsin=XI2=BU2. 2.8.3 Полная мощность. Кроме активной и реактивной мощностей цепь синусоидального тока характеризуется полной мощностью, обозначаемой S. Под полной мощностью участка понимают максимально возможную мощность при заданных напряжении U и токе I. Очевидно, что максимальная мощность получается при cos=l, т.е. при отсутствии сдвига фаз между напряжением и током: S=UI. Необходимость во введении этой мощности объясняется тем, что при конструировании электрических устройств, аппаратов, сетей и т.п. их рассчитывают на определенное номинальное напряжение Uноми определенный номинальный ток Iном и их произведение UномIном=Sном дает максимально возможную мощность данного устройства (полная мощность Sном указывается в паспорте большинства электрических устройств переменного тока). Для отличия полной мощности от других мощностей ее единицу называют вольт-ампер и сокращенно обозначают ВА. Есть формулы, связывающие эти мощности: 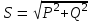 и и 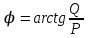 . .2.8.4 Мощность в комплексной форме. Все расчетные формулы для мощностей можно получать в комплексной форме. Составим произведение 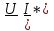 , где , где 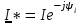 сопряженное комплексное значение тока. Произведение сопряженное комплексное значение тока. Произведение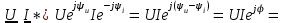 =UIcos+jUIsin=P+jQ. С другой стороны, 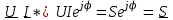 , где , где 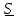 называется комплексной мощностью. Таким образом, называется комплексной мощностью. Таким образом,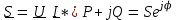 где P=Re( 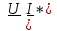 ); Q =Im( ); Q =Im(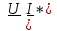 ) (Re действительная часть; Im мнимая часть). ) (Re действительная часть; Im мнимая часть).2.8.5 Баланс мощностей. Из закона сохранения энергии следует, что активная мощность источников равна активной мощности приемников, т.е. PИ=PП=RI2. Можно показать, что алгебраическая сумма реактивных мощностей источников равна алгебраической сумме реактивных мощностей приемников, т.е. QИ=QП=XI2. Так как равны активные и реактивные мощности источников и приемников, то равны и их полные мощности: SИ=SП. Приведенные равенства называют балансом мощностей. 2.8.6 Коэффициент мощности. Коэффициентом мощности называют отношение активной мощности Р к полной мощности 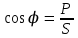 . .Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды и, в частности, используется на выполнение полезной работы. Пример 2.14 В цепь синусоидального тока (рисунок 2.28) последовательно включены две катушки и конденсатор с параметрами: R1=6 Ом, L1=0,016 Гн, R2=6 Ом, L2=0,032 Гн, C=320 мкФ. Определить активную, реактивную, полную мощности и коэффициент мощности при напряжении U=220 В и частоте 50 Гц. 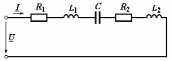 Рисунок 2.28 Решение. Реактивные сопротивления: XL1=L1=2500,0165 Ом; XL2=L2=2500,03210 Ом; 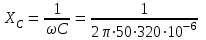 10 Ом. 10 Ом.Комплексное сопротивление 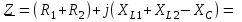 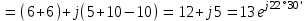 Ом. Ом.Ток (начальную фазу напряжения принимаем равной нулю) 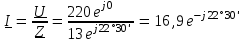 А. А.Комплексная мощность в показательной и алгебраической формах 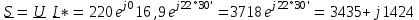 В·А. В·А.Полная мощность S=3718 В·А, активная мощность Р=3435 Вт, реактивная мощность Q=1424 вар (знак плюс показывает, что реактивная мощность Q=QL ), коэффициент мощности 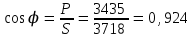 . .Пример 2.15 В цепи с последовательным соединением катушки с параметрами R, L с конденсатором (рисунок 2.29) плавно изменяется емкость С конденсатора. При максимальном токе в цепи сняты показания приборов: A=10 А, V=100 В, VC=250 В. Частота тока в цепи 50 Гц. Определить параметры цепи R, L, C и показания вольтметра, подключенного к выводам катушки. Решение. Так как ток максимальный, то в цепи имеет место резонанс напряжений, при котором UL=UC=250 В, UR=U=100 В. Напряжение на катушке 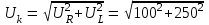 =269,3 В. =269,3 В.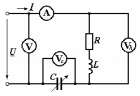 Рисунок 2.29 Емкостное сопротивление 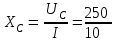 =25 Ом. =25 Ом.Емкость 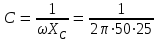 =1,27106 Ф=1,27 мкФ. =1,27106 Ф=1,27 мкФ.При резонансе XL=XC, поэтому Z=R и 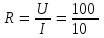 =10 Ом; =10 Ом; 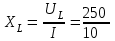 =25 Ом. =25 Ом.Из формулы XL=L индуктивность 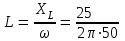 =7,96102 Гн=79,6 мГн. =7,96102 Гн=79,6 мГн.Пример 2.16 Напряжение на входах выводах контура (рисунок 2.30) U=100 В, частота f=50 Гц. Определить емкость С конденсатора, при которой в контуре возникает резонанс токов, и токи 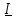 , , 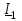 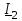 в режиме резонанса при R1=8 Ом, R2=3 Ом, XL=6 Ом. в режиме резонанса при R1=8 Ом, R2=3 Ом, XL=6 Ом.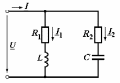 Рисунок 2.62 Решение. Из условия резонанса токов (BL=BC) следует, что 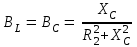 или или 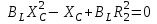 . . Так как 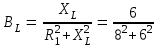 =0,06 См, то =0,06 См, то 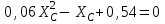 , , откуда 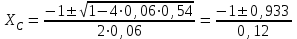 . .Это уравнение имеет два решения: XC1=16,1 Ом, 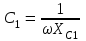 =197,7 мкФ =197,7 мкФ или XC2=0,0558 Ом, 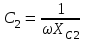 =5704 мкФ. =5704 мкФ.Из решения следует, что резонанс токов возможен при двух значениях емкости, однако практически целесообразно выбрать меньшую емкость, т.е. С1=197,7 мкФ. Токи в ветвях (принимая u=0): 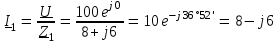 А; А;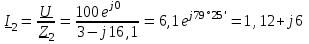 А; А; =9,12 А. =9,12 А.3 Трехфазные цепи переменного синусоидального тока Пример 3.1 К симметричной трехфазной линии с линейным напряжением UЛ=380 В подключены три одинаковых приемника, соединенных звездой с нейтральным проводом (рисунок 3.1). Активное и реактивное сопротивления каждого приемника соответственно равны: RФ=3 Ом, ХФ=4 Ом. Определить токи в фазах и нейтральном проводе, построить совмещенные топографическую диаграмму напряжений и векторную диаграмму токов. 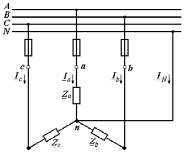 Рисунок 3.1 Решение. Так как нагрузка симметричная, то достаточен расчет одной фазы. Фазное напряжение 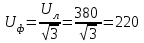 В, или в комплексной форме, принимая u=0, для фазы А получаем В, или в комплексной форме, принимая u=0, для фазы А получаем 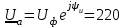 В. В.Комплексное сопротивление каждой фазы приемника 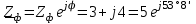 Ом. Ом.Ток 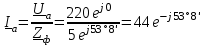 А. А.Ток в нейтральном проводе 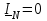 , так как нагрузка симметричная. , так как нагрузка симметричная.На рисунке 3.13 построены совмещенные топографическая диаграмма напряжений и векторная диаграмма токов. В каждой фазе фазный ток от фазного напряжения на угол =538`. Пример 3.2 К трехфазной линии напряжением Uл=380 В подключен несимметричный трехфазный приемник, соединенный звездой с нейтральным проводом (рисунок 3.2). Активные и реактивные сопротивления фаз приемника соответственно равны: Ra=19 Ом, Ха=0 Ом, Rb=8 Ом, Xb=6 Ом, Rc=24 Ом, Хс=18 Ом. Сопротивлениями проводов можно пренебречь. Определить токи в фазах приемника, в линейных проводах и в нейтральном проводе. 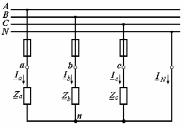 Рисунок 3.2 Решение. Токи в линейных проводах и фазах приемника одинаковы и рассчитываются по закону Ома: 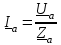 ; ; 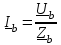 ; ; 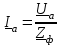 . .Фазное напряжение 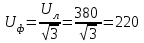 В. В.Комплексные фазные напряжения: 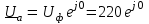 В; В; 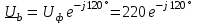 В; В;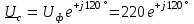 . .Комплексные сопротивления фаз: 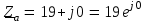 Ом; Ом; 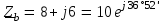 Ом; Ом;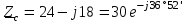 Ом. Ом.Токи в фазах приемника и проводах линии: 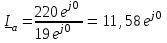 А; А; 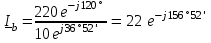 А; А;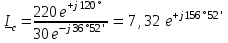 А. А.Ток в нейтральном проводе 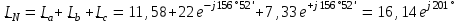 А. А.Для построения топографической диаграммы напряжений выберем масштаб напряжений. В выбранном масштабе строим топографическую диаграмму напряжений. При построении векторной диаграммы токов учтем, что токи в фазах сдвинуты относительно фазных напряжений на разные углы сдвига фаз: а=0 – нагрузка чисто активная (Х=0), b=3652 – нагрузка активно–индуктивная, с=3652 нагрузка активно–емкостная. Действующее значение тока в нейтральном проводе равно 16,14 А, а его начальная фаза N=201. На диаграмме (рисунок 3.3) строим векторы токов с учетом углов сдвига фаз. Вектор тока в нейтральном проводе можно построить двумя способами: или как сумму векторов, или непосредственно отложить вектор 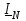 в соответствии с расчетными данными. в соответствии с расчетными данными.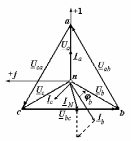 Рисунок 3.3 Пример 3.3 В схеме рисунок 3.1 (см. пример 3.1) сгорел предохранитель фазы а. Вычислить токи в двух других фазах и в нейтральном проводе. Построить совмещенные топографическую диаграмму напряжении и векторную диаграмму токов. Решение. Ток в фазе а после ее обрыва равен нулю ( 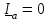 ), токи в фазах b и с не изменяются, так как в схеме с нейтральным проводом режимы фаз не зависят друг от друга. Вектор тока в нейтральном проводе может быть построен на векторной диаграмме как сумма векторов ), токи в фазах b и с не изменяются, так как в схеме с нейтральным проводом режимы фаз не зависят друг от друга. Вектор тока в нейтральном проводе может быть построен на векторной диаграмме как сумма векторов 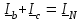 (рисунок 3.4). Из построений видно, что значение тока в нейтральном проводе равно действующему значению тока фазы b или с, т.е. IN=Iф=44 А. (рисунок 3.4). Из построений видно, что значение тока в нейтральном проводе равно действующему значению тока фазы b или с, т.е. IN=Iф=44 А.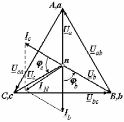 Рисунок 3.4 Пример 3.4 К трехфазной трехпроводной линии с напряжением Uл=660 В подключен симметричный приемник (рисунок 3.5) с сопротивлениями фазы R=8 Ом, Х=6 Ом. Определить токи в фазах приемника и в линейных проводах, построить топографическую диаграмму напряжений и совмещенную с ней векторную диаграмму токов. 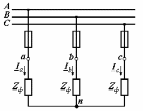 Рисунок 3.5 Решение. Так как нагрузка симметричная, то рассчитываем режим одной фазы. Фазное напряжение 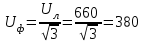 В, и в комплексной форме, принимая начальную фазу напряжения В, и в комплексной форме, принимая начальную фазу напряжения 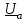 равной нулю, получаем равной нулю, получаем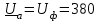 В. В.Комплексное сопротивление фазы 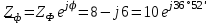 Ом (активно-емкостное). Ом (активно-емкостное).Фазный и линейный токи  А. А.Для построения совмещенных топографических диаграммы напряжений и векторной диаграммы токов (рисунок 3.6) выбираем масштаб напряжений и масштаб токов. Строим симметричную топографическую диаграмму напряжений; токи опережают соответствующие фазные напряжения на углы 3652. 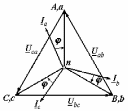 Рисунок 3.6 Пример 3.5 К трехпроводной трехфазной сети с линейным напряжением Uл=220 В подключен приемник, фазы которого соединены звездой (рисунок 3.7). Заданы сопротивления Ra=10 Ом, Rb=5 Ом, Хb=8,66 Ом, Хс=10 Ом. Определить токи в ветвях, построить совмещенную топографическую диаграмму напряжений и векторную диаграмму токов. Решение. Фазные напряжения источника образуют симметричную систему.  В; В;  В; В; В. В. Рисунок 3.7 Комплексные сопротивления фаз приемника:  =10 Ом; =10 Ом; 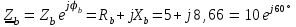 Ом; Ом;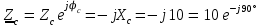 Ом, Ом,их комплексные проводимости 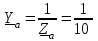 =0,1 См; =0,1 См;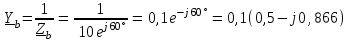 См; См;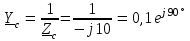 См. См.Смещение нейтрали 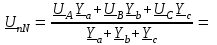 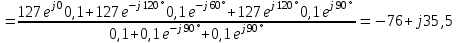 В. В.Фазные напряжения приемника: 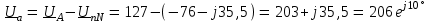 В; В; 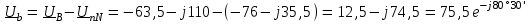 В; В;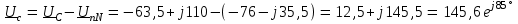 В. В.Фазные токи и токи в линии: 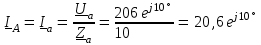 А; А;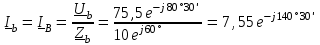 А; А;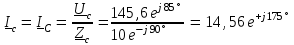 А. А.Для построения векторных диаграмм выбираем масштаб напряжения и тока. Строим симметричную топографическую диаграмму напряжений генератора и вектор смещения нейтрали 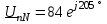 В. Векторы, соединяющие точку n и точки a, b, c, соответственно будут векторами фазных напряжений приемника В. Векторы, соединяющие точку n и точки a, b, c, соответственно будут векторами фазных напряжений приемника 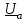 , , 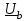 , , 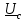 (рисунок 3.8). Из точки n строим векторы токов (рисунок 3.8). Из точки n строим векторы токов 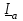 , , 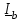 , , 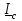 с учетом сдвига фаз относительно напряжений a=0, b=60, с=90. Топографическая диаграмма напряжении показывает, что из-за смещения нейтрали симметрия фазных напряжений приемника нарушается: Ua=206 В вместоUф=127 В; Ub=75,5 В; Uс=145,6 В. с учетом сдвига фаз относительно напряжений a=0, b=60, с=90. Топографическая диаграмма напряжении показывает, что из-за смещения нейтрали симметрия фазных напряжений приемника нарушается: Ua=206 В вместоUф=127 В; Ub=75,5 В; Uс=145,6 В.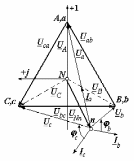 Рисунок 3.8 Пример 3.6 В трехфазной симметричной системе (см. пример 3.4) сгорел предохранитель фазы а приемника (рисунок 3.9). Определить токи в неповрежденных фазах и построить совмещенные топографическую диаграмму напряжений и векторную диаграмму токов. Решение. При обрыве одной из фаз симметрия системы нарушается. Проводимость оборванной фазы 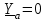 , проводимости неповрежденных фаз не изменяются. , проводимости неповрежденных фаз не изменяются.Смещение нейтрали 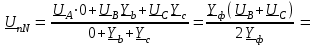 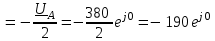 В. В.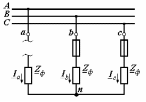 Рисунок 3.9 Напряжения на фазах приемника: 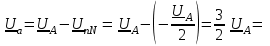 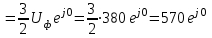 В; В;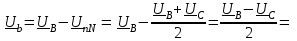 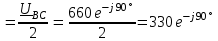 В; В;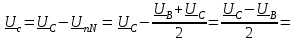 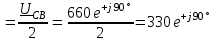 В. В.Токи в фазах приемника: 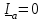 ; ; 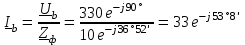 А; А;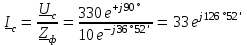 А; А;Для построения векторных диаграмм выбираем масштаб напряжения и тока. У генератора большой мощности линейные напряжения 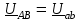 ; ; 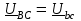 ; ; 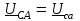 при обрыве фазы приемника не изменяются и на топографической диаграмме образуют замкнутый треугольник (рисунок 3.10). Нейтральная точки n при при обрыве фазы приемника не изменяются и на топографической диаграмме образуют замкнутый треугольник (рисунок 3.10). Нейтральная точки n при 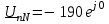 находится в середине вектора находится в середине вектора 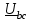 . Векторы, соединяющие точку n с точками a, b или c, соответственно будут векторами фазных напряжений приемника . Векторы, соединяющие точку n с точками a, b или c, соответственно будут векторами фазных напряжений приемника 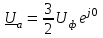 , , 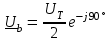 , , 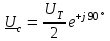 , ,что соответствует расчетным данным. Векторы токов 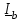 и и 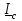 строим с учетом угла сдвига фаз =3652`. строим с учетом угла сдвига фаз =3652`.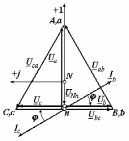 Рисунок 3.10 Пример 3.7 В трехфазной симметричной системе (см. пример 3.4) произошло короткое замыкание фазы а приемника (рисунок 3.11). Определить токи в фазах и построить совмещенные топографическую диаграмму напряжений и векторную диаграмму токов. Решение. При коротком замыкании фазы а сопротивление фазы 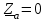 и потенциал точки n равен потенциалу точки а , т.е. на топографической диаграмме точка n совпадает с точкой а (рисунок 3.12) и и потенциал точки n равен потенциалу точки а , т.е. на топографической диаграмме точка n совпадает с точкой а (рисунок 3.12) и 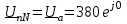 В. В.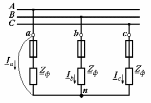 Рисунок 3.11 Напряжение на фазах приемника 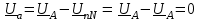 ; ;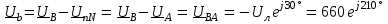 В; В;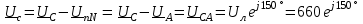 В. В.Токи в фазах b и с: 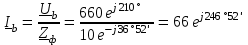 А; А;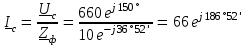 А. А.Ток фазы а находится по первому закону Кирхгофа. Для узла n : 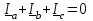 , ,откуда 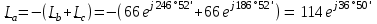 А. А.Для построения диаграмм (рисунок 3.12) выбираем масштаб напряжения и тока. Линейные напряжения 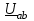 , , 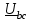 , , 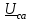 считаем заданными. Векторы, соединяющие точку n с точками b и с, соответственно будут равны фазным напряжениям считаем заданными. Векторы, соединяющие точку n с точками b и с, соответственно будут равны фазным напряжениям 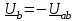 и и 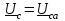 , что соответствует расчетным данным. Векторы токов , что соответствует расчетным данным. Векторы токов 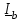 , , 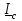 строим с учетом угла сдвига фаз =–3652. строим с учетом угла сдвига фаз =–3652.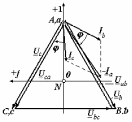 Рисунок 3.12 Пример 3.8 При напряжении и сопротивлениях фаз, заданных в примере 3.1, рассчитать фазные и линейные токи, если фазы приемника соединены треугольником (рисунок 3.13). Определить, как изменится линейный ток по сравнению с линейным током в схеме соединения фаз приемника звездой. Построить совмещенные топографическую диаграмму напряжений и векторную диаграмму токов. 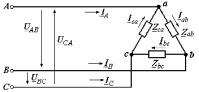 Рисунок 3.13 Решение При симметричной нагрузке действующие значения фазных токов одинаковы, поэтому рассчитываем режим одной фазы. Фазное напряжение равно линейному 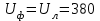 В. Комплексное сопротивление фазы В. Комплексное сопротивление фазы 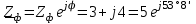 Ом. Действующее значение фазного тока Ом. Действующее значение фазного тока 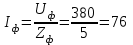 А. Согласно формуле А. Согласно формуле 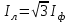 линейный ток линейный ток 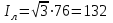 А. Линейный ток по сравнению с линейным током в схеме соединения фаз приемника звездой увеличивается в 3 раза, а фазный ток в А. Линейный ток по сравнению с линейным током в схеме соединения фаз приемника звездой увеличивается в 3 раза, а фазный ток в 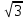 раз. раз.Для построения векторных диаграмм (рисунок 3.14) выбираем масштабы напряжения и тока. Фазные токи 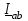 , , 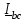 , , 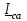 отстают по фазе от соответствующих фазных или равных им линейных напряжений на равные углы =538. отстают по фазе от соответствующих фазных или равных им линейных напряжений на равные углы =538. 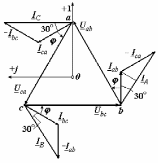 Рисунок 3.14 Пример 3.9 К трехпроводной трехфазной линии с линейным напряжением 380 В подключен трехфазный приемник с параметрами R=10 Ом, XL=10 Ом, XC=10 Ом (рисунок 3.15). Рассчитать токи в фазах и в линии, построить совмещенные топографическую диаграмму напряжений и векторную диаграмму токов. 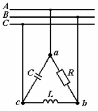 Рисунок 3.15 Решение. Сопротивления фаз по модулю одинаковые, но по аргументу разные; следовательно, нагрузка несимметричная и ток каждой фазы необходимо рассчитать отдельно. Комплексные сопротивления фаз: 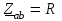 =10 Ом; =10 Ом; 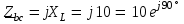 Ом; Ом;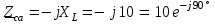 Ом. Ом.Комплексные линейные напряжения: 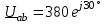 В; В; 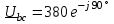 В; В; 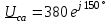 В. В.Фазные токи: 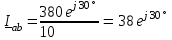 А; А; 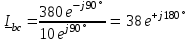 А; А;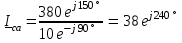 А. А.Линейные токи: 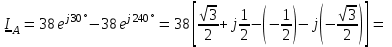 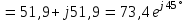 А; А;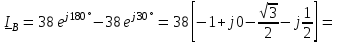 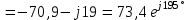 А; А;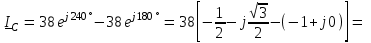 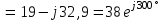 А. А.Для построения векторных диаграмм выбираем масштаб напряжения и тока. Строим топографическую диаграмму напряжений, аналогичную показанной на рисунке 3.14. Векторы фазных токов 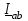 , , 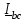 , , 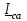 соответственно откладываем относительно векторов линейных напряжений соответственно откладываем относительно векторов линейных напряжений 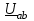 , , 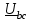 , , 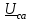 под углами ab=0, bc=90, ca=–90 (рисунок 3.16). Затем строим векторы под углами ab=0, bc=90, ca=–90 (рисунок 3.16). Затем строим векторы 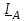 , , 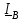 , , 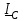 длина и направление, которых должны соответствовать расчетным данным. длина и направление, которых должны соответствовать расчетным данным.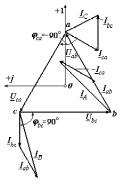 Рисунок 3.16 Пример 3.10 У симметричного трехфазного приемника (см. пример 3.8) произошел обрыв фазы ab (рисунок 3.17). определить токи в неповрежденных фазах и в линии, построить совмещенные топографическую диаграмму напряжений и векторную диаграмму токов. 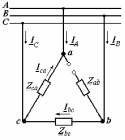 Рисунок 3.17 Решение. Токи в неповрежденных фазах не изменяются, так как фазные напряжения, равные линейным, не изменяются: Ica=Ibc=Iф=76 А. Линейные токи при 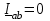 : :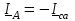 , ,  , , 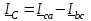 . .Из этих уравнений следует, что действующее значение линейных токов IA, IB равны действующим значениям фазных токов Ica=Icb=76 А , а у линейного тока IС действующее значение не изменяется, т.е. IC=132 А. Для построения векторной диаграммы выбираем масштабы напряжения и тока. Топографическая диаграмма линейных напряжений, равных фазным (рисунок 3.18). Векторы фазных токов 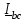 , , 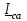 отстают по фазе относительно фазных напряжений отстают по фазе относительно фазных напряжений 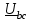 , , 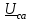 на углы =538. Линейные токи строим согласно полученным выше уравнениям. на углы =538. Линейные токи строим согласно полученным выше уравнениям. 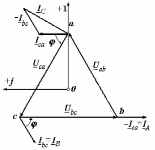 Рисунок 3.18 Пример 3.11 В симметричном трехфазном приемнике (см. пример 3.8) оборвался линейный провод. Определить фазные и линейные токи, построить совмещенные топографическую диаграмму напряжений и векторную диаграмму токов. Решение. Пусть оборвался провод А (рисунок 3.19). К приемнику проводится только напряжение 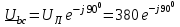 В. В. 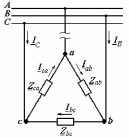 Рисунок 3.19 Сопротивление фазы bc включено полное напряжение 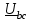 , а равные сопротивления фаз ab и ca включены последовательно и к каждому из них подведена половина напряжения , а равные сопротивления фаз ab и ca включены последовательно и к каждому из них подведена половина напряжения 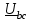 : :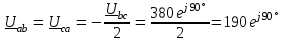 В. В.Ток фазы bc не изменяется: 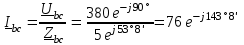 А. А.Фазные и линейные токи при 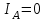 : :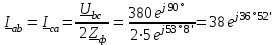 А; А;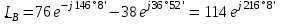 А; А;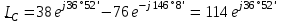 А. А.Совмещенная диаграмма представлена на рисунке 3.20. 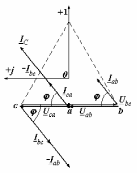 Рисунок 3.20 Пример 3.12 К трехфазной линии с UЛ=380 В подключены трехфазный симметричный приемник, фазы которого соединены треугольником, и группа однофазных приемников, соединенных звездой с нейтральным проводом (рисунок 3.21). Комплексное сопротивление фазы симметричного приемника 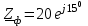 Ом. Активные мощности однофазных приемников Ра=5500 Вт, Рb=3300 Вт, Рc=7700 Вт при cosф=1. Сопротивлением проводов можно пренебречь. Определить: фазные и линейные токи симметричного приемника, токи в несимметричных приемниках, суммарные активную, реактивную и полную мощности. Ом. Активные мощности однофазных приемников Ра=5500 Вт, Рb=3300 Вт, Рc=7700 Вт при cosф=1. Сопротивлением проводов можно пренебречь. Определить: фазные и линейные токи симметричного приемника, токи в несимметричных приемниках, суммарные активную, реактивную и полную мощности.Решение. Фазные напряжения при соединений звездой с нейтральным проводом 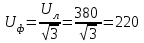 В. В.Фазные токи однофазных приемников: 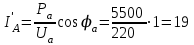 А. А.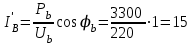 А. А.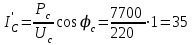 А. А.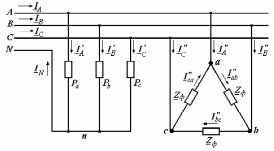 Рисунок 3.21 Фазные и линейные токи трехфазного приемника: 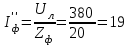 А; А; 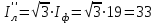 А. А.и его активная и реактивная мощности 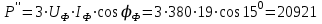 Вт; Вт;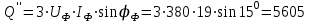 вар. вар.Суммарные мощности: 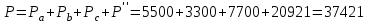 Вт; Вт;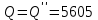 вар; вар; 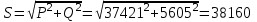 ВА. ВА.4 Электрические машины и основы электропривода 4.1 Трансформаторы Трансформатор представляет собой статическое электромагнитное устройство, предназначенное для преобразования переменного (синусоидального) тока одного напряжения в переменный ток другого напряжения той же частоты. Трансформаторы широко применяются в разных областях электротехники, радиотехники, электроники, в устройствах измерения, автоматического управления и регулирования. По особенностям конструкции и применению трансформаторы можно разделить на силовые, сварочные, измерительные и специальные. наибольшее применение в народном хозяйстве получили иловые трансформаторы, которые являются необходимым элементом промышленной электрической сети. У трансформатора две основные части: магнитопровод и обмотки. Трансформаторы большой мощности, кроме того, имеют систему охладения. Магнитопровод изготовляют из горячекатанной или холоднокатанной листовой электротехнической стали. При частоте тока до 150 Гц магнитопровод собирают из листов электротехнической стали толщиной 0,35 или 0,5 мм. |
