Рро. методичка+к+решению+кр. Учебнометодическое пособие для выполнения расчетнографических работ и проведения практических занятий

• Название: Учебнометодическое пособие для выполнения расчетнографических работ и проведения практических занятий
• Дата: 27.12.2022
• Размер: 2.03 Mb.
• Имя файла: методичка+к+решению+кр.docx
• Тип: Учебно-методическое пособие; #866630
• страница: 3 из 11

Рисунок 1.7

Их взаимное эквивалентное преобразование во многих случаях позволяет упростить схему и свести ее к схеме смешанного соединения сопро­тивлений.

По условию эквивалентности преобразований при тех же токах I_a, I_b, I_c в обеих схемах напряжения U_ab, U_bc, U_ca после преобразования измениться не должны.

Рассмотрим преобразование треугольника сопротивле­ний в эквивалентную звезду.

Запишем уравнение по второму закону Кирхгофа для контура треугольника:

R_abI_ab+R_bcI_bc+R_caI_ca=0.

Для узлов a и b треугольника в соответствии с первым за­коном Кирхгофа

I_ca=I_abI_a; I_bc=I_ab+I_b.

Подставив это выражение в предыдущую формулу, получим:

R_abI_ab+R_bcI_ab+R_bcI_b+R_caI_ab–R_caI_a=0.

откуда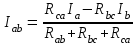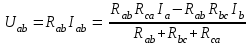

;

.

Для звезды сопротивлений напряжение U_ab равно раз­ности падений напряжения на сопротивлениях R_a и R_b:

U_ab=R_aI_aR_bI_b.

Сравнивая последние две формулы, получаем: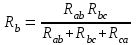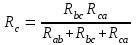

;

;

.

Эти формулы позволяют преобразовать треугольник сопротивлений в эквивалентную звезду сопро­тивлений.

Формулы обратного преобразования – звезды сопро­тивлений в треугольник  можно получить, заменив все сопротивления проводимостями.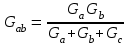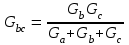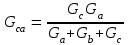

;

;

.

Пример 1.5 Задана мостовая схема (рисунок 1.8,а). Сопротивления и ЭДС схемы известны. Требуется найти ток в сопротивлении R.

Решение.

Заменим треугольник сопротивлений R_ab, R_bc, R_caэквивалентной звездой сопротивлений R_a, R_b, R_cкоторая на рисунке 1.8,a показана штриховой линией. В результате получим схему рисунок 1.8,б со смешанным соединением сопротивлений. Эквивалентное сопротивле­ние этой схемы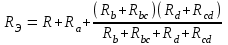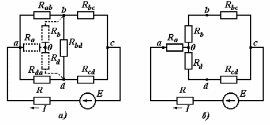

.



Рисунок 1.8

Решение. Заменим треугольник сопротивлений R_ab, R_bc, R_caэквивалентной звездой сопротивлений R_a, R_b, R_cкоторая на рисунке 1.8,a показана штриховой линией. В результате получим схему рисунок 1.8,б со смешанным соединением сопротивлений. Эквивалентное сопротивле­ние этой схемы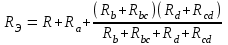

.

Ток в неразветвленной части цепи .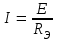

1.1.4 Преобразование ветвей с источниками ЭДС. При последовательном соединении нескольких источников ЭДС (рисунок 1.9,а) разность потенциалов (напряжение) между точками а и b:

V_a–V_b=U_ab=R_nI+E_m+...+R₂I+E₂+R₁I-E₁=E_k + R_kI.

Обозначим

E_k=E_э и =R_k=R_э.

Напряжение U_ab=E_Э–R_ЭI, что соответствует эквивалент­ной схеме (рисунок 1.9,б). Таким образом, эквивалентная ЭДС равна алгебраической сумме последовательно соединен­ных ЭДС, а эквивалентное сопротивление  арифметиче­ской сумме последовательно соединенных сопротивлений.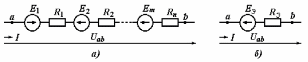