|
|
Рро. методичка+к+решению+кр. Учебнометодическое пособие для выполнения расчетнографических работ и проведения практических занятий
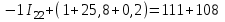 . .
I11=2 A; I22=3 A; I33=8 A.
Токи в ветвях:
I1=I11=2 A; I2=I11I22=2(3)=5 A; I3=I22+I33=
=(3)+8=11 A; I4=I33=8 A.
1.1.7 Метод двух узлов. Этот метод применяется для расчета электрических цепей с двумя узлами, между которыми включены активные и пассивные ветви (рисунок 1.14). Идея метода состоит в том, что по расчетной формуле определяется напряжение между узлами, называемое узловым напряжением Uab, а затем по закону Ома рассчитываются токи в ветвях.
Выведем формулу для расчета узлового напряжения. Положительные направления токов в ветвях выберем от узла а к узлу b. Напряжение Uab узловое напряжение, общее для всех ветвей схемы.
Токи в ветвях по закону Ома:
I1=(Uab E1)G1; I2=UabG2;
I3=(Uab + E3)G3; … ; In=(Uab + En)Gn.
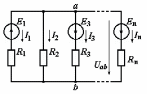
Рисунок 1.14
Запишем первый закон Кирхгофа для узла а. Подставляя значения токов в ветвях, имеем:
(Uab E1)G1 + UabG2 + (Uab + E3)G3 + … + (Uab + En)Gn=0
или
E1G1 E3G3 + ... + EnGn =Uab(G1 + G2 + G3 + … + Gn).
Напряжение между узлами
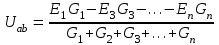
или в общем виде
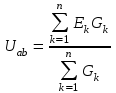 . .
Если ЭДС направлена к узлу, обозначенному первым, индексом (а), то произведение EkGk записывается со знаком плюс, если от узла со знаком минус независимо от положительных направлений токов. Если в ветви нет ЭДС, то произведение EkGk=0.
Пример 1.9 Решить пример 1.7 методом двух узлов.
Решение. Рассчитаем проводимости ветвей (см. рисунок 1.13):
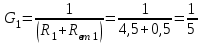 См; См; 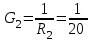 Cм; Cм;
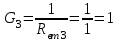 См; См; 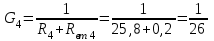 См. См.
Узловое напряжение Uab (положительное направление от узла aк узлу b) равно:
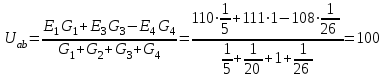 В. В.
Токи в ветвях:
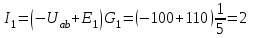 А; А; 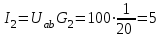 А; А;
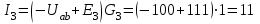 А; А;
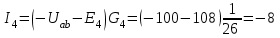 А. А.
1.1.8 Принцип и метод наложения. Этот принцип является выражением одного из основных свойств линейных систем любой физической природы и применительно к линейным электрическим цепям формулируется следующим образом: ток в какой-либо ветви сложной электрической цепи равен. алгебраической сумме частичных токов, вызванных каждым действующим в цепи источником электрической энергии в отдельности.
Использование принципа наложения позволяет во многих случаях упростить задачу расчета сложной цепи, так как она заменяется несколькими относительно простыми цепями, в каждой из которых действует один источник энергии. Из принципа наложения вытекает метод наложения для расчета электрических цепей.
Метод наложения и порядок расчета. Рассмотрим порядок расчета на примере определения токов в схеме (рисунок 1.15,а). Заданную схему разобьем на вспомогательные, число которых равно числу ветвей с источниками электрической энергии (в данном примере две вспомогательные схемы по рисунку 1.15,б и в). Выберем произвольно положительные направления всех токов и обозначим все величины, относящиеся к какой-либо вспомогательной схеме, соответствующим числом штрихов.
Рассчитаем токи вспомогательных схем, в которых, исключая все ЭДС, кроме одной, оставляем все сопротивления, включая внутренние сопротивления источников.
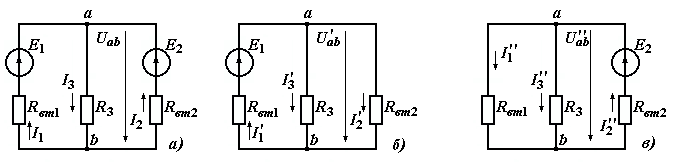
Рисунок 1.15
Для схемы на рисунке 1.15, б:
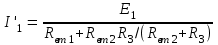 ; ; 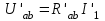 ; ;
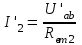 ; ; 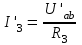 ; ;
Для схемы на рисунке 1.15, в:
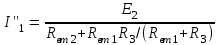 ; ; 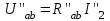 ; ;
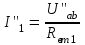 ; ; 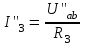 . .
Токи в ветвях заданной схемы согласно принципу наложения равны алгебраическим суммам соответствующих токов вспомогательных схем:
I1=I1I1; I2=I2+I2; I3=I3+I3.
1.1.9 Метод эквивалентного генератора (активного двухполюсника). Метод эквивалентного генератора дает возможность часть сложной электрической цепи с источниками энергии и двумя выделенными выводами, т.е. активный двухполюсник (рисунок 1.16,а), заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на выводах двухполюсника и внутреннее сопротивление входному сопротивлению двухполюсника. Если в активный двухполюсник входят все элементы схемы, кроме одного выделенного сопротивления R, то можно найти ток I в этом сопротивлении. Поэтому метод эквивалентного генератора рационально применять, если необходимо найти ток в одной ветви сложной электрической цепи, не рассчитывая токи в других ветвях.
Доказательство метода. В сложной электрической цепи (рисунок 1.16,а), показанной в виде активного двухполюсника А с выделенным участком, сопротивление которого R, требуется найти ток I. Включим последовательно с сопротивлением R два источника ЭДС: Е' и Е" (рисунок 1.16,б), с напряжениями, равными напряжению между выводами а и b активного двухполюсника при отключенном сопротивлении R, т.е. в режиме холостого хода Е'=Е"=Ux, и направленными навстречу друг другу. Ток I при этом не изменится.
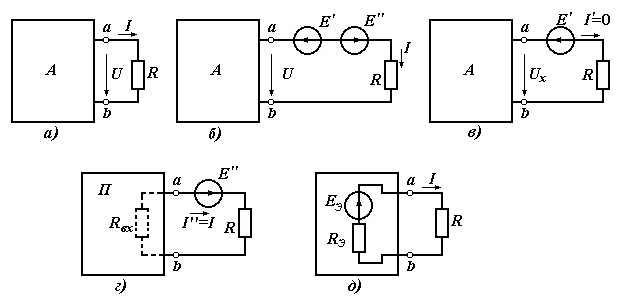
Рисунок 1.16
В соответствии с принципом наложения схему (рисунок 1.16,б) можно представить в виде двух вспомогательных схем, в одной из которых действует источник ЭДС Е' и все источники внутри активного двухполюсника (рисунок 1.16,в), а в другой (рисунок 1.16,г) действует только источник ЭДС Е", а источник Е' и все источники в активном двухполюснике не действуют, т.е. активный двухполюсник становится пассивным.
По принципу наложения ток I равен сумме частичных токов вспомогательных схем: I=I'+I''. Так как Е'=Е"=Ux, то во вспомогательной схеме рисунка 1.16,в частичный ток I' равен нулю, что следует из закона Ома:
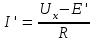
Следовательно, частичный ток I" (рисунок 1.16,г) равен искомому току I. По закону Ома
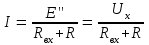
где Rвх внутреннее или входное сопротивление пассивного двухполюсника, т.е. сопротивление пассивного двухполюсника (рисунок 1.16,г) относительно выводов а и b. Такой же ток будет и в схеме рисунка 1.16,д, если ЕЭ=Ux и RЭ=Rвх. Ток I в сопротивлении исходной схемы (рисунок 1.16,а) и в схеме рисунок 1.16,д один и тот же, т.е. активный двухполюсник можно заменить эквивалентным генератором.
Порядок расчета. Для расчета тока в сопротивлении R следует сначала отключить это сопротивление и определить напряжение Ux на его выводах. Далее нужно исключить все ЭДС в оставшейся части схемы (внутренние сопротивления источников остаются) и найти ее сопротивление относительно выводов отключенного сопротивления. Наконец, рассчитать искомый ток.
Пример 1.10 Для схемы по рисунку 1.17, а заданы ЭДС и сопротивления: Е1=72 В, Е2=48 В, R1=3 Ом, R2=4 Ом, R3=12 Ом. Найти ток I3 в ветви с сопротивлением R3.
Решение.
В соответствии с порядком расчета отключим сопротивление R3 и найдем напряжение Uх (рисунок 1.17,б) по:
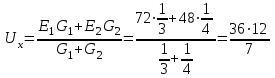 В. В.
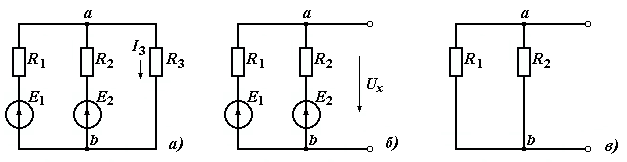
Рисунок 1.17
Входное сопротивление между выводами а иb при исключенных ЭДС Е1 и Е2 (рисунок 1.17,в)
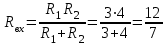 Ом Ом
(сопротивления R1 и R2 включены параллельно).
Ток
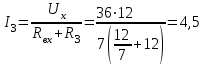 А. А.
2 Электрические цепи переменного
синусоидального тока
2.1 Общие сведения
Понятие «синусоидальный ток» относится ко всем периодическим токам, изменяющимся во времени по синусоидальному закону. Наибольшее распространение в энергетике получили электрические цепи синусоидального тока. По сравнению с постоянным током синусоидальный имеет ряд преимуществ: производство, передача и использование электрической энергии наиболее экономичны при синусоидальном токе. В цепях синусоидального тока в отличие от постоянного можно относительно просто преобразовывать напряжения (получать напряжения различных значений) при сохранении формы кривой напряжения. Самыми простыми, надежными, экономичными и, следовательно, наиболее распространенными являются электрические двигатели трехфазного синусоидального тока синхронные двигатели. Синусоидальные токи широко используются в радиоэлектронике, электротехнологии, контрольно-измерительной технике и других областях. Теория однофазных синусоидальных токов служит базой для изучения более сложных видов токов: трехфазных синусоидальных и других периодических токов.
2.1.1 Основные величины, характеризующие синусоидальные функции времени. В линейных цепях синусоидального тока и напряжение, и ЭДС, и ток являются синусоидальными функциями времени:
u=Umsin(t+u); e=Emsin(t+e); i=Imsin(t+i),
здесь и, е, i — соответственно мгновенные значения напряжения, ЭДС, тока, т.е. значения этих величин в рассматриваемый момент времени; t+u, t+e, t+i аргументы синусоидальных функций, называемые фазой или фазовым углом. Фаза отсчитывается от точки перехода синусоидальной функции через нуль к положительному значению. Синусоидальные напряжение и и ток i показаны на рисунке 2.1.
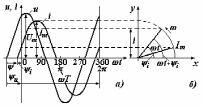
Рисунок 2.1
Каждая синусоидальная функция времени однозначно определяется тремя параметрами:
амплитудойUm,Em,Im (максимальное значение синусоидальной функции);
угловой частотой (скорость изменения аргумента синусоидальной функции), где в рад/с;
начальной фазой u, е, i (значение аргумента синусоидальной функции в момент начала отсчета времени, т. е. при t=0) в радианах или градусах.
Кроме того, для характеристики синусоидальных функций времени используют следующие величины:
1) период 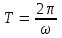 наименьший интервал времени, по истечении которого мгновенные значения периодической величины повторяются; наименьший интервал времени, по истечении которого мгновенные значения периодической величины повторяются;
2) частота 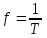 , т. е. число периодов в секунду. Единица частоты герц (Гц) (1 Гц=1 с1); , т. е. число периодов в секунду. Единица частоты герц (Гц) (1 Гц=1 с1);
3) сдвиг фаз между напряжением и током алгебраическая величина, определяемая как разность начальных фаз, напряжения и тока: =ui. Сдвиг фаз между одноименными синусоидальными величинами (токами, напряжениями, ЭДС) принято обозначать другой буквой, например ;
4) действующее значениеU,E,I среднеквадратичное значение переменной величины за период. Наименование «действующее» объясняется тем, что тепловой и силовой эффекты синусоидального тока за период равны эффекту постоянного тока, значение которого равно действующему значению синусоидального тока за тот же интервал времени. Так, при синусоидальном токе за период Т в сопротивлении R та же электрическая энергия преобразуется в тепловую, что и при равном его действующему значению постоянном токе за то же время:
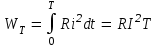
В соответствие с определением действующее, т.е. среднеквадратичное, значение синусоидального тока
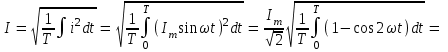
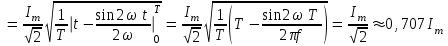 . .
Аналогично определяются действующие значения напряжения и ЭДС:
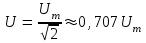 ; ; 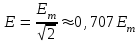 . .
Важно знать, что в паспорте электротехнических устройств синусоидального тока указаны действующие значения напряжений и токов и что большинство приборов, применяемых для измерений синусоидальных напряжений и токов, градуированы в действующих значениях;
5) среднее значение Iср, Uср, Eср. Среднее значение синусоидальной функции за период равно нулю (одинаковые площади положительной и отрицательной полуволн синусоиды). Поэтому условились под средним значением синусоидальной функции понимать ее среднее значение за положительный полупериод (мгновенные значения положительные).
Мгновенное значение тока i=Imsin(t+i). Среднее значение тока за положительный полупериод не зависит от начальной фазы, поэтому примем i =0. По определению среднего значения имеем:
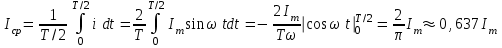 . .
Аналогично определяются средние значения напряжения и ЭДС:
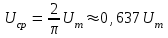 ; ; 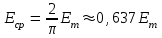 . .
2.2 Представление синусоидальных функций в различных формах
2.2.1 Аналитическое представление синусоидальных функций. Синусоидальную функцию можно аналитически задать тригонометрической формулой i=Imsin(t+i). Для расчета электрических цепей такое выражение неудобно, так как алгебраические действия с тригонометрическими функциями приводят к громоздким вычислениям. Так, сумма синусоидальных токов i1=I1msin(t+i1) и i2=I2msin(t+i2) равна:
i=i1+ i2=I1msin(t+i1)+ I2msin(t+i2)= Imsin(t+i),
где  ; ;
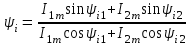 . .
Графическое представление синусоидальных величин (рисунок 2.1,а) достаточно наглядно, но из-за сложности построения синусоид применяется сравнительно редко.
2.2.2 Представление синусоидальных функций при помощи векторов. Оно позволяет наглядно показать количественные и фазовые соотношения в цепях синусоидального тока и широко применяется при объяснении физических процессов и выводе основных соотношений.
В прямоугольной системе координат хОу (рисунок 2.1,б) отложим вектор 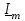 (векторы, изображающие синусоидальные функции времени, обозначаются буквами, подчеркнутыми снизу). Длина вектора должна быть равна амплитуде тока, а угол наклона к оси абсцисс начальной фазе тока i. Его проекция на ось ординат Imsiniравна мгновенному значению тока в момент времени t=0, т.е. i(0)=Imsini. Будем вращать вектор (векторы, изображающие синусоидальные функции времени, обозначаются буквами, подчеркнутыми снизу). Длина вектора должна быть равна амплитуде тока, а угол наклона к оси абсцисс начальной фазе тока i. Его проекция на ось ординат Imsiniравна мгновенному значению тока в момент времени t=0, т.е. i(0)=Imsini. Будем вращать вектор 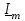 с постоянной угловой скоростью вокруг начала координат против направления движения часовой стрелки. За время t вектор 1т повернется на угол t относительно начального положения, так что угол наклона к оси абсцисс станет равным (t+i). с постоянной угловой скоростью вокруг начала координат против направления движения часовой стрелки. За время t вектор 1т повернется на угол t относительно начального положения, так что угол наклона к оси абсцисс станет равным (t+i).
Проекция вращающегося вектора на ось ординат i= Imsin(t+i) и представляет собой мгновенное значение тока синусоидальную функцию.
В электротехнике векторы изображают не вращающимися, а неподвижными для момента времени t=0 (рисунок 2.2) и их масштабы выбирают так, чтобы длина вектора соответствовала не амплитуде, а действующему значению. Углы наклона к оси абсцисс равны начальным фазам (i, u). Таким образом, неподвижные векторы определяют два параметра синусоидальной функции: действующее значение или амплитуду и начальную фазу. Третий параметр угловая частота должен быть известен.
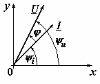
Рисунок 2.2
Угол между вектором напряжения и вектором тока равен углу сдвига фаз =ui. Если u>>i (как на рисунке 2.2), то >0 и напряжение опережает по фазе ток на угол сдвига фаз . В противном случае <0 и напряжение отстает по фазе от тока. Угол всегда откладывается от вектора тока 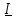 к вектору напряжения к вектору напряжения 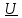 . .
Совокупность векторов ЭДС, напряжений и токов, изображенных в общей системе координат, называют векторной диаграммой, которая дает наглядное представление об амплитудах (действующих значениях), начальных фазах и углах сдвига фаз указанных величин. При вращении векторов с общей угловой скоростью их взаимное положение зависит не от начальных фаз, а от углов сдвига фаз.
2.2.3 Представление синусоидальных функций при помощи комплексных чисел. От векторного изображения синусоидальных функций можно перейти к их выражению комплексными числами.
На комплексной плоскости с осями координат +1 ось действительных чисел и величин и +j ось мнимых чисел и величин (рисунок 2.5) (в электротехнике в отличие от математики мнимую единицу 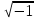 обозначают j, так как буква i принята для обозначения мгновенного значения тока) отложим вектор обозначают j, так как буква i принята для обозначения мгновенного значения тока) отложим вектор 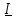 длиной I под углом i к действительной оси. Его проекцию на ось действительных чисел обозначим I, на ось мнимых чисел I. Любая точка на комплексной плоскости или вектор, проведенный из начала координат в эту точку, изображается комплексным числом длиной I под углом i к действительной оси. Его проекцию на ось действительных чисел обозначим I, на ось мнимых чисел I. Любая точка на комплексной плоскости или вектор, проведенный из начала координат в эту точку, изображается комплексным числом 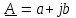 , где а координата точки по оси действительных чисел; b по оси мнимых чисел. Поэтому вектор тока , где а координата точки по оси действительных чисел; b по оси мнимых чисел. Поэтому вектор тока 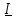 может быть записан в комплексной форме может быть записан в комплексной форме 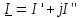 . Такая запись комплексных чисел или величин называется алгебраической формой. . Такая запись комплексных чисел или величин называется алгебраической формой.
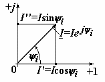
Рисунок 2.3
Из рисунка 2.3 следует, что I=Icosi и I=Isini. Поэтому вектор 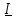 можно записать и в так называемой тригонометрической форме: можно записать и в так называемой тригонометрической форме:
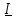 = Icosi +j Isini. = Icosi +j Isini.
Принимая во внимание формулу Эйлера 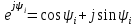 тот же вектор запишем еще в показательной форме: тот же вектор запишем еще в показательной форме: 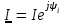 , где модуль вектора I и начальная фаза iпредставляют собой полярные координаты вектора. , где модуль вектора I и начальная фаза iпредставляют собой полярные координаты вектора.
Выражение 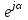 называют оператором поворота, так как умножение на называют оператором поворота, так как умножение на 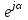 какого-либо вектора какого-либо вектора 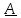 равносильно повороту этого вектора на комплексной плоскости на угол (рисунок 2.4). Угол i показывает поворот вектора равносильно повороту этого вектора на комплексной плоскости на угол (рисунок 2.4). Угол i показывает поворот вектора 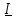 относительно оси действительных величин (рисунок 2.3). относительно оси действительных величин (рисунок 2.3).
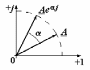
Рисунок 2.4
Таким образом, вектор 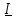 может быть выражен тремя различными комплексными формами записи: может быть выражен тремя различными комплексными формами записи:
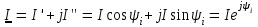 . .
Переход от алгебраической формы записи к показательной и тригонометрической выполняется по формулам, которые следуют из рисунка 2.3:
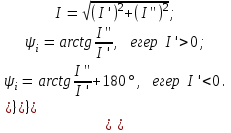 . .
Таким образом, комплексное число отображает вектор и, так же как вектор, определяет два параметра синусоидальной функции амплитуду (действующее значение) и начальную фазу, третий параметр синусоидальной функции должен быть известен.
Величины 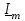 , , 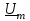 , , 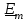 называют комплексными амплитудами соответственно тока, напряжения, ЭДС, а называют комплексными амплитудами соответственно тока, напряжения, ЭДС, а 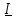 , , 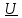 , , 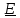 комплексными действующими значениями тока, напряжения, ЭДС или, короче, комплексным током, комплексным напряжением, комплексной ЭДС. комплексными действующими значениями тока, напряжения, ЭДС или, короче, комплексным током, комплексным напряжением, комплексной ЭДС.
Пример 2.1 Дано комплексное действующее значение тока I=4j3. Найти параметры синусоидальной функции времени – мгновенного значения тока, соответствующего заданному комплексному числу.
Решение.
Действующее значение тока
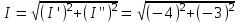 =5 А; =5 А;
Амплитуда тока
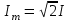 =7,07 А; =7,07 А;
начальная фаза тока
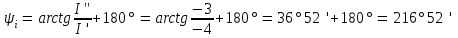 . .
Искомое мгновенное значение тока
i=Imsin(t+i)=7,07sin(t+21652) А.
Угловая частота предполагается известной.
Пример 2.2 Заданы параметры синусоидального тока: амплитуда 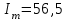 А, начальная фаза i=30, угловая частота =314 рад/с. Требуется записать мгновенное значение тока, рассчитать его комплексное действующее значение в трех формах. А, начальная фаза i=30, угловая частота =314 рад/с. Требуется записать мгновенное значение тока, рассчитать его комплексное действующее значение в трех формах.
Решение.
i=Imsin(t+i)=56,5sin(314t30) А;
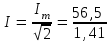 40 А; 40 А;
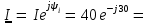 40cos(30)+jsin(30)=34,7j20 А. 40cos(30)+jsin(30)=34,7j20 А.
Пример 2.3 Заданно комплексное напряжение 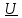 =400+j300; частота =400+j300; частота 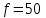 Гц. Требуется найти мгновенное значение напряжения u. Гц. Требуется найти мгновенное значение напряжения u.
Решение. Комплексное напряжение 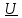 из алгебраической формы переведем в показательную из алгебраической формы переведем в показательную
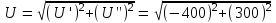 =500 В; =500 В;
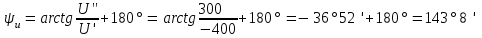 ; ;
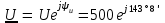 В. В.
По известному действующему значению напряжения определим его амплитуду
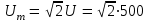 707 В; 707 В;
угловая частота
=2f =250314 рад/с;
мгновенное значение напряжения
u=Umsin(t+u)=707sin(314t+1438) В.
2.2.4 Алгебраические операции с комплексными числами. Как было показано, комплексные числа отображают векторы, а векторы синусоидальные функции времени. Поэтому операции с комплексными числами отображают соответствующие операции с векторами и синусоидальными функциями. Например, сложение двух комплексных чисел означает сложение двух векторов и, следовательно, сложение двух синусоидальных функций.
При сложении и вычитании комплексных чисел или величин следует пользоваться алгебраической формой записи комплексных чисел или величин. Например, два синусоидальных тока заданы в комплексной форме: 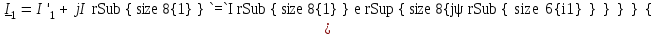 , , 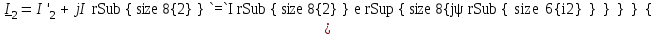 . При их сложении или вычитании алгебраически суммируются действительные и мнимые части: . При их сложении или вычитании алгебраически суммируются действительные и мнимые части:
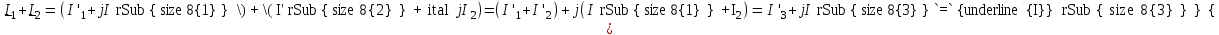 ; ;
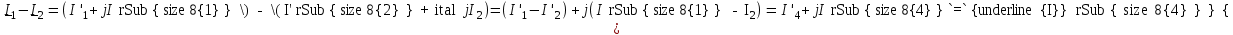 . .
При умножении, делении и логарифмировании предпочтительнее пользоваться показательной формой чисел или величин:
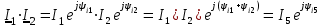 ; ;
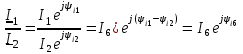 ; ;
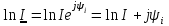 , ,
Расчеты с применением комплексных чисел упрощаются при применении микрокалькуляторов. Переход от алгебраической формы записи комплексного числа к показательной форме и наоборот соответствует переходу от декартовых координат к полярным и от полярных координат к декартовым.
|
|
|
 Скачать 2.03 Mb.
Скачать 2.03 Mb.