Методичка - Статистика. Учебнометодическое пособие Иркутск, 2012 удк 616. 31 314. 144 Ббк 51. 1(2)2 56. 6 А49 Учебнометодическое пособие
 Скачать 1.5 Mb.
|
Основные понятия и определения по темеВсе явления в природе и в обществе находятся во взаимной связи. Каждый специалист в результате своей деятельности определяет наличие связи изучаемых явлений, их материальную природу, ее направленность (прямая и обратная), вид связи. Различают две формы (вида) связи:
В свою очередь корреляционная связь может быть:
Кроме того, связь между признаками различается по направлению. Так, когда изменение одного явления ведет к изменению другого явления в том же направлении, (рост экономической обеспеченности ведет к улучшению питания населения) отмечается прямая (положительная) связь и наоборот, когда явления изменяются в разных направлениях (снижение заболеваемости полиомиелитом при увеличении числа привитых) говорят об обратной (отрицательной) связи. Закономерность корреляционной связи пробивается через случайность при массовых наблюдениях. И изучается она статистическими методами – вычислением коэффициентов корреляции. Таблица 1 Схема оценки характера и силы корреляционной связи по коэффициентам корреляции
Коэффициенты корреляции Коэффициент корреляции рангов (Спирмена) (ро) – рассчитывается по формуле:  , где 6 – постоянный коэффициент, n – число коррелируемых пар, d – разность рангов (между порядковыми номерами рядов), Σ – знак суммы. Условиями использования коэффициента ранговой корреляции являются:
Методика вычисления коэффициента ранговой корреляции: I этап – присвоение рангов (порядковых номеров) по каждому ряду числовых значений признака. При наличии нескольких одинаковых значений изучаемого признака, ранги присваиваются одни и те же и соответствуют они средней их порядковых номеров. II этап – вычисление разности между рангами в каждой паре коррелируемых признаков. III этап – рассчитывается квадрат разности рангов и определяется их сумма. IV этап – рассчитывают коэффициент ранговой корреляции. Пример: Измерение корреляции между смертностью от рака молочной железы и от рака шейки матки методом рангов (на 100000 женщин в 5 районах). Таблица 2 Матрица расчета коэффициента ранговой корреляции Спирмена (ρ)
При присвоении рангов (в примере от большей смертности к меньшей) при одинаковых величинах явления в ряду, ранги берутся в среднем из суммы их очередных порядковых номеров. Так 19,1 – 1 ранг, 16,0 – 2-ой, следующий тоже 16,0 – 3-ий, так как значения одинаковые, берем: (2+3)/2=5/2=2,5 и каждому одинаковому уровню присваиваются одинаковые ранги равные среднему значению. В нашем примере – 2,5. По выше приведенной формуле вычисляем коэффициент рангов:  =-0,8Для определения достоверности коэффициента корреляции рангов вычисляется его ошибка по формуле:  mρ0,4Достоверность коэффициента корреляции рангов определяется по формуле:  Доверительный коэффициент t должен быть равен или больше 3, что соответствует вероятности 99%, то есть корреляционная связь существенна, если t меньше 3-х – несущественна. При числе наблюдений n<9 существенность полученного коэффициента рангов оценивается по таблице (В.Ю. Урбаха). (Приведена в сокращенном виде). Таблица 3 Критические значения коэффициента корреляции рангов (ρ)
Если число наблюдений (n) равно 9 и более существенность полученного коэффициента можно оценивать по таблице t-критерия (Стьюдента) для числа степеней свободы n' = n – 2, t определяется по вышеприведенной или по следующей формуле:  ;Вывод. В рассматриваемом примере при n=5, t=2, ρ=-0,8 нельзя утверждать, что между смертностью от рака молочной железы и смертностью от рака шейки матки существует какая-то зависимость, так как ρ=-0,8 меньше критического уровня =0,94 при n=5 по таблице В.Ю. Урбаха и t=2 меньше 3-х. Коэффициент линейной корреляции (метод Пирсона) Коэффициент корреляции с использованием для вычисления его отклонения d каждой вариаты V от средней М этого ряда рассчитывается в простых вариационных рядах X и Y по формуле: 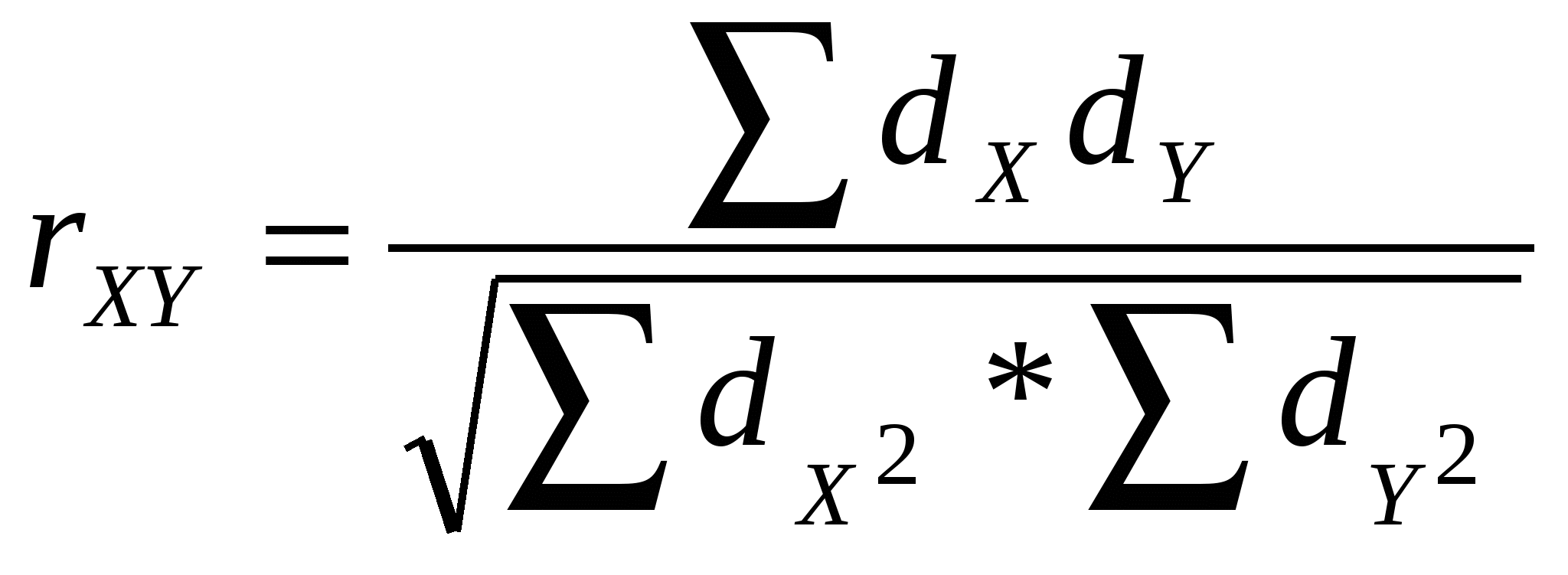 , где n – число парных чисел в корреляционных рядах (групп вариант).d = V – М Средняя ошибка коэффициентов корреляции равна:  Величина коэффициента корреляции считается достоверной, если он не менее чем в 3 раза превышает свою среднюю ошибку:  и более.Коэффициент корреляции rXY дает возможность вычислить коэффициент регрессии RXY – степень изменения величины одного признака – X при соответствующем изменении другого – Y и наоборот по формуле:  и наоборот  ; σX и σY – средние квадратические отклонения вариационного ряда X и Y.Коэффициент регрессии используется в статистике физического развития населения для составления оценочных таблиц. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||