Методичка - Статистика. Учебнометодическое пособие Иркутск, 2012 удк 616. 31 314. 144 Ббк 51. 1(2)2 56. 6 А49 Учебнометодическое пособие
 Скачать 1.5 Mb. Скачать 1.5 Mb.
|
Контрольные вопросы
Глава 4. Динамические ряды и их анализ Цель занятия: Ознакомить студентов с методикой расчета и анализа показателей динамического ряда. План занятия:
Основные понятия и определения по темеВажной задачей медицины и здравоохранения является изучение здоровья населения и объема деятельности лечебно-профилактических учреждений с учетом их изменений во времени, то есть в динамике по периодам, годам, месяцам, дням недели. Для анализа динамики применяются динамические ряды. Динамический ряд – это ряд, состоящий из однородных сопоставимых величин, характеризующих изменение какого-либо явления за определенный промежуток времени. Числа, составляющие динамический ряд, принято называть уровнями (U). Уровни могут быть представлены абсолютными, относительными и средними величинами. Следует помнить, что динамический ряд должен состоять из чисел, характеризующих одно и то же явление и в одинаковых единицах измерения. Не рекомендуется сравнивать в динамике экстенсивные величины (удельный вес), так как величина их изменения зависит от соотношения внутри совокупности. Динамический ряд не только дает возможность проанализировать динамику развития какого-либо явления, но и выявить рост и снижение его, отдельные «всплески», «пики» с анализом их причин, что важно для планирования работы врача, подразделения, службы. Динамические ряды могут быть:
Если числовые значения признака динамического ряда имеют значительные колебания, что затрудняет выявление закономерностей развития явления, производится выравнивание динамического ряда. Методы выравнивания динамического ряда:
Например: на Н-ском меланжевом комбинате простудные заболевания в случаях на 100 работающих в период с 1989 по 1996 годы составляли: Таблица 1 Выравнивание показателей динамического ряда
Вывод: Анализируя сам показатель – число случаев на 100 работающих, трудно судить о тенденции его изменения. Проведя выравнивание динамического ряда (любым способом), можно уже говорить о тенденции снижения показателя. Метод наименьших квадратов Динамика развития лучше всего может быть выражена линией, которая наиболее близко подходит к фактическим данным. Это достигается методом наименьших квадратов, который наиболее объективно выявляет тенденцию развития изучаемого явления. Сначала определяется характер изменения изучаемого явления. В зависимости от характера кривой определяют характер уравнения зависимости между явлением и временем. Имеется много различных уравнений, выражающих зависимость между двумя изучаемыми явлениями. Например, если тенденция прямолинейная, то она представляется в виде прямой линии, уравнение которой y = a + bx (парабола I порядка). Если тенденция криволинейная, то она может быть представлена в виде параболы II порядка (уравнение y = a + bx +cx2), параболой III порядка (y = a + bx +cx2 + dx3) или параболой n-го порядка. Чаще всего в практике здравоохранения используется выравнивание по параболе I и II порядка. Проведем выравнивание показателей младенческой смертности, имеющих прямолинейную тенденцию развития, по способу наименьших квадратов, используя параболу I порядка (табл. 2). Таблица 2 Выравнивание показателей младенческой смертности по параболе I порядка
Y1981=32,2+(-2,17)*(-4)=40,9 Y1981=32,2+(-2,17)*(-3)=38,7 и т.д. Для определения точности выравнивания (аппроксимации) используют формулу: 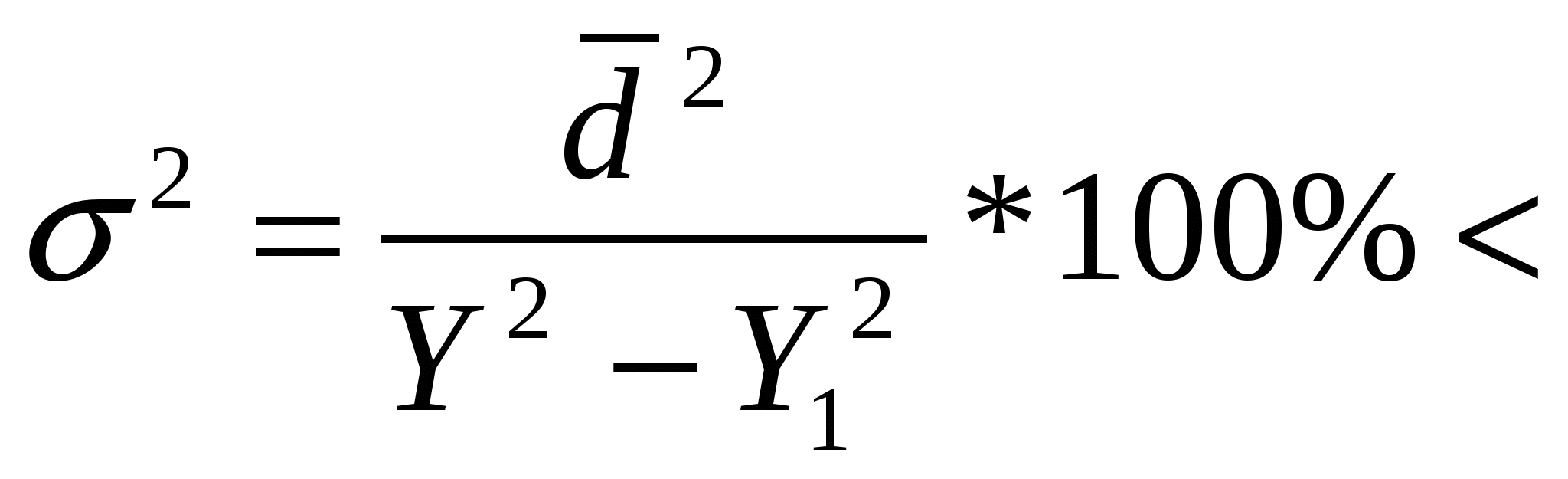 5% 5%Таблица 3 Определение точности выравнивания
Чтобы определить, как быстро (интенсивно) изменяется это явление, необходимо вычислить показатели динамического ряда. Показатели динамического ряда:
ТИПОВОЕ ЗАДАНИЕ: Проследить динамику обеспеченности населения N-ской области больничными койками терапевтического профиля (на 10 000 жителей). Таблица 4 Матрица расчета показателей динамического ряда
ПРИМЕР РАСЧЕТА ПОКАЗАТЕЛЕЙ ДИНАМИЧЕСКОГО РЯДА: 1. Расчет абсолютного прироста: в 2009 г. 30,0-30,8= -0,8 в 2011 г. 27,0-28,5= -1,5 в 2010 г. 28,5-30,0= -1,5 в 2012 г. 26,9-27,0= -0,1 2. Расчет темпа прироста: в 2009 г. в 2010 г. 3. Расчет темпа роста: в 2009 г. в 2010 г. 4. Расчет содержания 1% прироста: в 2009 г. в 2010 г. Вывод: Показатель обеспеченности населения N-ской области больничными койками терапевтического профиля с 2009 по 2012 год имеет стойкую тенденцию к снижению. За 5 лет абсолютная убыль обеспеченности населения терапевтическими койками составила 3,9 койки на 10 000 жителей. Наиболее интенсивно показатель снижался в 2010 и 2011 годах. Таким образом, анализ динамического ряда предусматривает:
|
