Учебнометодическое пособие к лабораторным работам Красноярск 2018 Составители Иртюго Л. А. Дидух С. Л
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Экспериментальная часть Реактивы, приборы, посуда: - кварцевая коническая или круглодонная колба, 250мл, - перманганат калия 0,1 н раствор, - концентрированный раствор перекиси водорода (Н2О2), - раствор фенола от 0,03 до 3 М, - установка для изучения фотохимических реакций, - секундомер. Последовательность выполнения работы. Целью данной работы является исследование кинетики реакции фотохимического разложения перекиси водорода в водном растворе Изучение кинетики фотохимического разложения перекиси водорода в водном растворе проводится на установке, изображенной на рис. 4.1. 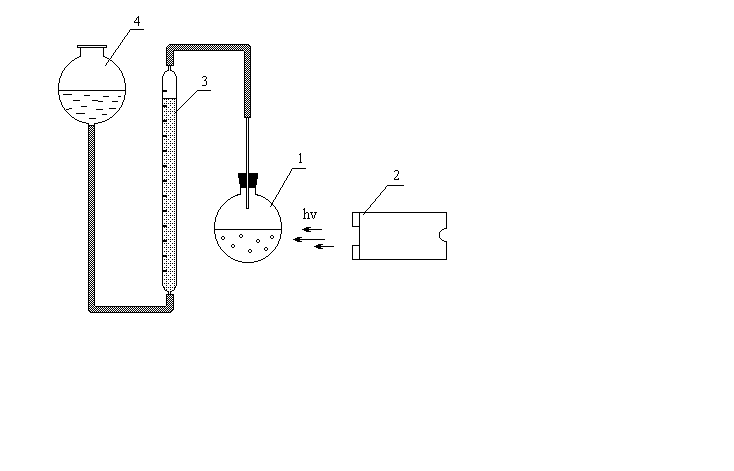 . .Рис. 4.1. Установка для изучения фотохимического разложения перекиси водорода Раствор перекиси водорода в кварцевой колбе 1 облучают ультрафиолетовым светом от источника 2. Разлагаясь, Н2О2 выделяет кислород, объем которого измеряется с помощью градуированной бюретки 3, соединенной с уравнительным сосудом 4. Перед работой следует промыть кварцевую колбу хромовой смесью и тщательно прополоскать дистиллированной водой. Затем налить в колбу, разведенную до определенной концентрации (по указанию преподавателя) перекись водорода. Концентрацию исследуемого раствора перекиси определяют титрованием 5 мл этого раствора 0,1 н. перманганатом калия. По количеству взятой перекиси рассчитывают предельный объем кислорода, который может выделиться при полном разложении. Колбу устанавливают против отверстия защитного кожуха ртутно-кварцевой лампы. Устанавливают на нуль уровень жидкости в измерительной бюретке, подняв при этом уравнительный сосуд до совпадения уровней. Необходимо удостовериться в герметичности установки. Для этого опускают уравнительную склянку ниже уровня бюретки. Уровень воды в бюретке при этом опустится и установится на некотором делении. Если это положение не изменится в течение 3 мин, установку можно считать герметичной. В противном случае уровень воды в бюретке будет непрерывно расти. Затем включают лампу. Одновременно с зажиганием лампы пускают секундомер. Отсчеты времени производят, когда объем выделяющегося газа изменится на определенную величину (0,5 – 1 мл). Каждый отсчет проводят после выравнивания уровней бюретки и сосуда 4. Опыт прекращают, когда не происходит определение газа в течение 5 – 10 мин. После окончания опыта необходимо выключить лампу, вновь тщательно промыть кварцевую колбу. Фотохимический распад перекиси водорода обладает повышенной чувствительностью к наличию в растворе примесей и состоянию стенок реакционного сосуда. Изучить скорость этого процесса можно, не только изменяя концентрацию взятой перекиси, но и проводя несколько последовательных опытов при одинаковой концентрации, добавляя для замедления скорости реакции до 3 мл 0,03 М раствора фенола. Скорость реакции зависит также от интенсивности облучения. Для изучения влияния этого параметра можно либо изменять расстояние между реакционной колбой и источником облучения, либо менять длительность облучения, проводя его лишь первые 15 – 30 мин. Фотохимический распад можно изучать также в зависимости от диаметра реакционного сосуда, используя колбы разного объема. Экспериментальные данные заносят в таблицу: Таблица 4.1
По полученным данным строят кинетическую кривую в координатах VO2 =f(τ). Дифференцируя полученный график, находят значения скорости реакции в каждый момент времени: 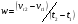 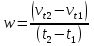 . .Задание: построить графики зависимости: 1. w = f( 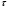 ). ).2. lgw=f( 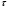 ). ).Логарифмическая форма уравнения (4.1) скорости цепной реакции является уравнением прямой 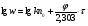 . (4.3) . (4.3)В связи с убылью исходного вещества в ходе реакции имеет смысл обрабатывать по этому уравнению только данные, относящиеся к восходящей ветви кривой w = f( 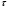 ). ).Построив график в координатах lgw, 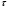 , по отрезку, отсекаемому на оси ординат, находят значение kn0 , а по тангенсу угла наклона прямой – константу нарастания , по отрезку, отсекаемому на оси ординат, находят значение kn0 , а по тангенсу угла наклона прямой – константу нарастания 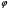 . Затем по соотношению (4.2) рассчитывают период индукции. . Затем по соотношению (4.2) рассчитывают период индукции.Контрольные вопросы 1. Какие параметры оказывают влияние на скорость фотохимической, цепной реакции? 2. В чем отличие цепных реакций от каталитических, автокаталитических и простых сопряженных реакций? 3. Как можно сократить или удлинить период индукции? 4. Какое значение в практике имеют цепные фотохимические реакции? 5. Нарисуйте зависимость скорости цепной реакции от времени при условии, что количество центров бесконечно возрастает. Работа №5 Изучение кинетики топохимических реакций Теоретическое введение Образование и диссоциация карбонатов, восстановление окислов и сульфидов, производство цемента, огнеупоров, керамики и многие другие химические превращения являются сложными гетерогенными процессами, имеющими огромное практическое значение. Их особенность состоит в том, что химическая стадия процесса сопровождается превращением в твердом состоянии, когда вещество с одной кристаллической решеткой исчезает и образуется продукт с другой структурой. Простейший пример такой реакции – диссоциация 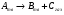 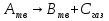 . Указанные реакции называют топохимическими. Для них характерно нарастание скорости в начальный период процесса и достижение ею предельного значения с последующим постепенным спадом до нуля (рис. 5.1, кривая 2). Одним из внешних признаков топохимической реакции служит S–образный вид кинетической кривой (рис. 5.1, кривая 1). . Указанные реакции называют топохимическими. Для них характерно нарастание скорости в начальный период процесса и достижение ею предельного значения с последующим постепенным спадом до нуля (рис. 5.1, кривая 2). Одним из внешних признаков топохимической реакции служит S–образный вид кинетической кривой (рис. 5.1, кривая 1).Рис. 5.1. Кинетика топохимической реакции: зависимости степени превращения (1) и скорости реакции (2) от времени процесса. Топохимическая реакция начинается обычно на отдельных участках поверхности, в так называемых потенциальных центрах реакции, откуда она постепенно распространяется в глубь кристалла. Центры реакции – места на поверхности кристалла, где связи частиц в решетке ослаблены (вершины углов, ребра, дефекты на поверхности). В первый период реакции образуются микроскопические зародыши ядер новой фазы (реакция идет с ничтожной скоростью). Образование зародышей ядер, в свою очередь, вызывает искажение материнской решетки, которое способствует возникновению новых зародышей. Одновременно увеличиваются и сами ядра, поверхность реакции растет, в результате растет скорость химического взаимодействия. Этот период является автокаталитическим, так как образование продукта реакции, приводящее к увеличению поверхности раздела фаз, вызывает возрастание скорости. Скорость процесса будет максимальной при наибольшей величине поверхности реакции, когда межфазные границы отдельных зон, центров приходят в соприкосновение. После того, как зоны перекрываются, поверхность начинает уменьшаться и скорость реакции падает. Для того чтобы получить уравнение кинетики топохимической реакции, нужно знать или предположить, по крайней мере, следующие основные параметры: - закон образования ядер новой фазы; - закон роста ядер; - форму ядер. Возможны различные сочетания законов образования, роста и формы ядер продукта, поэтому существует большое количество уравнений, описывающих кинетику топохимических реакций. Но наиболее широко применяются лишь несколько из них. На основании вероятности взаимодействия молекул данной системы и вне связи с предположениями об истинном механизме реакции Ерофеев получил уравнение 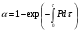 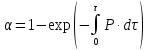 , (5.1) , (5.1)где – доля прореагировавших молекул к моменту времени ; P – вероятность того, что молекулы прореагируют в течение времени от до 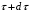 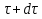 . Определив Р, можно получить кинетическое уравнение соответствующего процесса. В общем случае вероятность взаимодействия молекул в любой момент времени пропорциональна суммарной поверхности реакции, т.е. . Определив Р, можно получить кинетическое уравнение соответствующего процесса. В общем случае вероятность взаимодействия молекул в любой момент времени пропорциональна суммарной поверхности реакции, т.е. 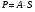 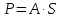 . Примем, что поверхность реакции изменяется во времени по степенному закону . Примем, что поверхность реакции изменяется во времени по степенному закону 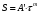 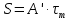 . Тогда . Тогда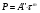 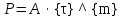 , (5.2) , (5.2)где A, A`, A`` – коэффициенты пропорциональности. Подставляя (5.2) в (5.1), получим 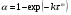 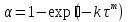 . (5.3) . (5.3)Здесь k и m – эмпирические коэффициенты. m = r + n, где r имеет смысл числа элементарных стадий при превращении зародыша в активно растущее ядро, а n зависит от числа направлений, в которых растут ядра (может быть равным 1, 2, 3). Коэффициенту k иногда приписывается смысл константы скорости. Величины k и m находят графически по экспериментальным данным. Для этого уравнение (6.3) представляют в линейной форме 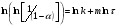 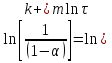 (5.4) (5.4)и по графику в координатах 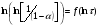 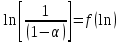 определяют k и m. определяют k и m.Экспериментальная часть Реактивы, приборы, посуда: - исследуемое вещество – перманганат калия (KMnO4), - экспериментальная установка для изучения топохимических реакций. Последовательность выполнения работы. Схема экспериментальной установки для изучения кинетики топохимических реакций с выделением газа изображена на рис. 5.2. 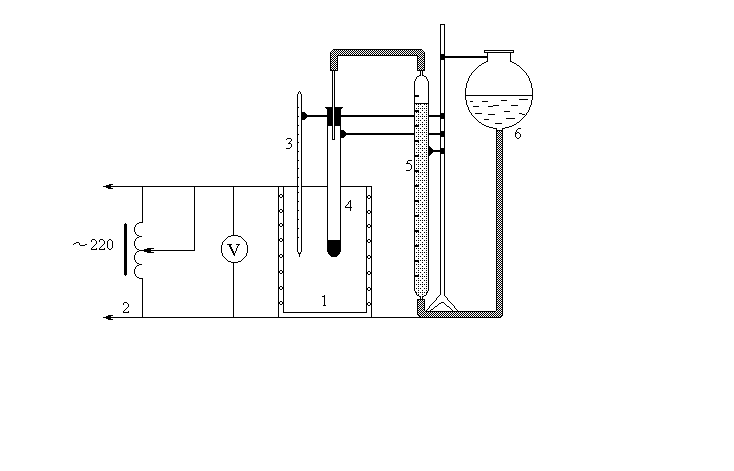 Рис. 5.2. Схема экспериментальной установки Она состоит из печи сопротивления 1, температура в которой регулируется лабораторным автотрансформатором 2, термометра 3 для измерения температуры в печи, пробирки 4 с исследуемым веществом, газометрической бюретки 5 с уравнительным сосудом 6 для измерения объема выделяющегося при реакции газа. В ходе работы необходимо построить кинетические кривые термического разложения исследуемого вещества при двух температурах заданных преподавателем (260 – 315 ͦС). Порядок проведения всех измерений одинаков, и они производятся с равными навесками вещества. Автотрансформатор включают в сеть переменного тока и согласно градуировочной кривой выставляют нужное напряжение, соответствующее нижней температуре опыта. Пробирку и термометр располагают рядом по центру шахты печи так, чтобы нижний срез находился примерно в середине зоны нагревателя. После того как температура установится постоянной на заданной величине и будет неизменной в течение 10 мин, в пробирку засыпают навеску исследуемого вещества ( 0,3 г), плотно закрывают пробкой на отводном шланге, включают секундомер и отмечают первое показание на бюретке. Время между отсчетами следует выбирать, исходя из необходимости построения точной кинетической кривой. Как правило, в начале и конце реакции отрезки времени более продолжительны и с повышением температуры уменьшаются. Наиболее целесообразно производить отсчеты времени, в течение которого объем выделяющегося газа изменится на определенную величину (0,5 – 1 мл). Окончанием реакции считают время, когда объем газа в бюретке в течение 10–15 минут остается неизменным. После окончания опыта исследуемое вещество извлекают из реакционной пробирки и вновь взвешивают для определения потери веса gоп в результате реакции. Полученное значение сравнивают с весом выделившегося газа и теоретическим значением gт, рассчитанным по стехиометрическому уравнению, предполагая, что реакция идет до конца. Если в качестве исследуемого вещества взят перманганат калия KМnO4, то реакция его разложения в суммарном виде может быть выражена уравнением 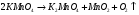 , ,справедливым для температур вблизи 2000С. Экспериментальные данные следует представить в виде табл. 5.1 (для каждой температуры), где V – объем газа в данный момент времени; V – конечный объем выделившегося газа. Таблица5.1
Также необходимо построить графики для каждой исследованной температуры:
Контрольные вопросы 1. В чем заключаются особенности топохимических реакций? 2. Анализ обобщенной кинетической кривой ( 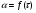 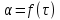 ): начальный период, периоды индукции, ускорения и спада. ): начальный период, периоды индукции, ускорения и спада.3. Законы зародышеобразования. 4. Суть концепции зародышеобразования по разветвленному цепному механизму. 5. Анализ уравнения Праута-Томпкинса. 6. Анализ уравнения Ерофеева. Работа №6 Изучение кинетики испарения жидкости и диффузии ее паров в воздухе Теоретическое введение Всякий гетерогенный процесс включает в себя несколько стадий. Основные из них транспорт реагирующих веществ к реакционной поверхности, собственно химическая реакция, отвод продуктов реакции в объем. В зависимости от условий проведения процесса и его особенностей наиболее медленной может быть любая из трех стадий. Если лимитирующими являются первая и третья стадии, то скорость процесса зависит от скорости переноса вещества посредством диффузии. Такой режим называют диффузионным. Большое значение имеют диффузионные влияния в процессах испарения жидкостей и сублимации твердых тел. Они играют ведущую роль при сушке, перегонке и т.д. – везде, где скорость процесса лимитируется отводом пара от поверхности конденсированной фазы. Процесс диффузии подчиняется первому закону Фика 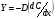 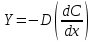 , (6.1) , (6.1)где 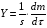 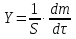 – количество вещества m, проходящее за время dt через сечение S (диффузионный поток, г/см2×с); D – коэффициент диффузии; – количество вещества m, проходящее за время dt через сечение S (диффузионный поток, г/см2×с); D – коэффициент диффузии; 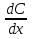 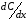 – градиент концентрации. – градиент концентрации.Знак «–» показывает, что диффузия идет в направлении убывания концентрации. Величина D представляет собой удельную скорость диффузии, т.е. количество вещества, проходящего в единицу времени через единицу поверхности при единичном градиенте концентрации. Как следует из выражения (6.1), коэффициент D имеет размерность D = (длина)2/время, а выражают его обычно в см2/с. С повышением температуры коэффициент диффузии возрастает экспоненциально в жидкостях и твердых телах 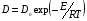 и по степенной зависимости в газах 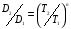  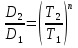 . .Значение показателя степени в последнем уравнении лежит обычно в пределах 1,6 – 2,0. Кинетическая сторона диффузии ясна из следующих рассуждений. Если на границе раздела фаз концентрация испаряющегося вещества равна Сs, а на расстоянии d – С и равна концентрации в глубине объема V, то можно приближенно заменить 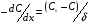 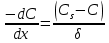 . (6.2) . (6.2)Тогда вместо выражения (6.1) получим 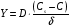 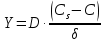 . (6.3) . (6.3)Разделив обе части уравнения (6.3) на объем и переходя к концентрации, получим 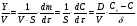 . .Отсюда скорость диффузии запишется 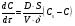 . (6.4) . (6.4)Таким образом, скорость диффузии кинетически подчиняется уравнению первого порядка относительно концентрации в объеме. Интегрирование (6.4) дает обычное выражение для константы массопереноса 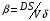 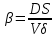 , которая является аналогом константы скорости , которая является аналогом константы скорости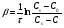 , ,где С0 – начальная концентрация диффундирующего вещества в объеме. Диффузия – процесс относительно медленный. Это объясняется тем, что каждая молекула диффундирующего вещества испытывает огромное число соударений и перемещается по сложной траектории, длина которой несоизмеримо велика по сравнению с расстоянием, проходимым молекулой в направлении диффузии. Вследствие этого лишь небольшая часть молекул, вырвавшихся из жидкости, успевает удалиться от ее поверхности на значительное расстояние. В тонком слое газа над самой поверхностью накапливаются молекулы испаряющегося вещества, и парциальное давление паров растет до тех пор, пока не станет почти равным давлению насыщенного пара. В общем случае говорят: если процесс лимитируется диффузией, то около поверхности раздела фаз устанавливается состояние, близкое к равновесному. Для экспериментального определения коэффициентов диффузии чаще всего создают такие условия, в которых процесс испарения и диффузии паров протекает стационарно. В стационарном процессе скорость его, а также концентрация вещества в любой точке системы не меняются со временем. Такой процесс диффузии легко рассчитать. Например, для описания скорости стационарного испарения жидкости в вертикальной цилиндрической трубе, у верхнего среза которой поддерживается постоянное парциальное давление паров Р0, Стефан получил уравнение 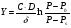 , ,которое позволяет выразить коэффициент диффузии через измеряемые в опыте величины 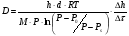 , (6.5) , (6.5)где М – молекулярный вес жидкости; Р – давление атмосферное; Рs – давление насыщенных паров жидкости при температуре Т; d – плотность жидкости; h – расстояние от поверхности жидкости до верхнего среза трубы; Dh – измерение высоты уровня жидкости в результате испарения за время Dt; R – универсальная газовая постоянная. Анализ нестационарного процесса испарения жидкости из вертикальной цилиндрической трубы показывает, что данный процесс должен подчиняться уравнению 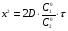 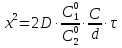 , (6.6) , (6.6)где х – расстояние, на которое переместилась в трубке граница жидкость – пар за время t; С20 – концентрация воздуха на межфазной границе (кг/м3); С10 – концентрация насыщенного пара жидкости на границе (кг/м3); 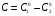 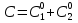 . .Экспериментальная часть Реактивы, приборы, посуда: - ацетон, - пробирки, - штатив с держателем, - катетометр. Последовательность выполнения работы. В штатив помещают две тонкие (4–6 мм диаметром) стеклянные пробирки. Одна из них служит для определения коэффициентов диффузии пара жидкости при стационарном процессе испарения по уравнению Стефана (6.5) (метод 1), другая – для расчета скорости нестационарного испарения по уравнению (6.6) (метод 2). Метод 1.Исследуемую жидкость наливают в пробирку на 50–80 мм ниже ее верхнего среза. Через 15–20 мин, в течение которых происходит установление стационарного состояния, начинают измерения при помощи катетометра (приложение 3). Измерять Dh нужно с большой точностью, так как испарение идет медленно и Dh выражается десятыми долями миллиметра. Отсчеты снимают через 5 мин. За время опыта снимают 6 – 7 отсчетов и строят график 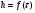 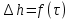 , позволяющий судить о стационарности процесса испарения ( , позволяющий судить о стационарности процесса испарения (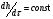 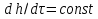 ). Измерения заносят в таблицу и представляют в виде графика ). Измерения заносят в таблицу и представляют в виде графика 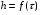 , из которого определяют значение , из которого определяют значение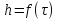 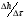 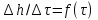 . По уравнению (6.5) рассчитывают коэффициент диффузии пара жидкости в воздухе. В данной работе ввиду сложностей определения Р0, его значение принимают равным нулю, хотя это можно делать только в случае полного удаления паров у среза трубки, что выполняется, например, при измерении коэффициентов диффузии паров методом увлечения. За высоту h принимают среднее ее значение за время опыта (высота диффузионного пространства): . По уравнению (6.5) рассчитывают коэффициент диффузии пара жидкости в воздухе. В данной работе ввиду сложностей определения Р0, его значение принимают равным нулю, хотя это можно делать только в случае полного удаления паров у среза трубки, что выполняется, например, при измерении коэффициентов диффузии паров методом увлечения. За высоту h принимают среднее ее значение за время опыта (высота диффузионного пространства):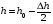 . .Метод 2. Пробирку заполняют исследуемой жидкостью полностью до верхнего среза. Измерения перемещения межфазной границы во времени производят катетометром, сразу после заполнения с промежутками между измерениями 2 мин. Всего снимают 10 отсчетов. Измерения заносят в таблицу и представляют в виде графиков: 1. х = f(t); 2. х2 = f(t); 3. зависимость скорости испарения 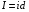 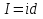 от t. от t.i – скорость перемещения межфазной границы, 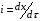 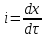 . По тангенсу угла наклона второго графика с учетом давления насыщенного пара исследуемой жидкости при температуре опыта рассчитываютD и сравнивают с полученным значением по методу 1 и литературными данными. . По тангенсу угла наклона второго графика с учетом давления насыщенного пара исследуемой жидкости при температуре опыта рассчитываютD и сравнивают с полученным значением по методу 1 и литературными данными.Концентрации С10 и С20 на межфазной границе находят по формуле 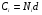 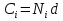 (Ni – мольная доля газа, равная отношению парциального давления газа к общему давлению), используя взятое из справочника значение давления насыщенного пара жидкости при температуре опыта и рассчитывая плотность пара жидкости dn, считая его идеальным газом: (Ni – мольная доля газа, равная отношению парциального давления газа к общему давлению), используя взятое из справочника значение давления насыщенного пара жидкости при температуре опыта и рассчитывая плотность пара жидкости dn, считая его идеальным газом: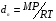 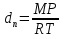 . .Контрольные вопросы 1. Как зависит скорость испарения жидкости от температуры? 2. По каким признакам можно судить о том, в каком режиме идет процесс: в кинетическом или диффузионном? 3. Что такое диффузия и каков физический смысл коэффициента диффузии? 4. Какова температурная зависимость коэффициента диффузии? 5. Что означает выражение «стационарный режим процесса», «нестационарный режим процесса»? 6. Каковы условия применимости уравнения Стефана? 7. Сформулируйте первый и второй законы Фика. Работа №7 Изучение кинетики растворения и диффузии в водных растворах Теоретическое введение Многие гетерогенные реакции идут в диффузионном режиме. Это особенно относится к высокотемпературным реакциям, имеющим промышленное значение. Как правило, скорости таких процессов в неподвижной среде очень малы, и поэтому их стараются повысить, прибегая к размешиванию при помощи специальных приспособлений. Перенос вещества в движущейся жидкости обусловлен двумя различными механизмами. Во-первых, при наличии разности концентраций в жидкости возникает молекулярная диффузия в соответствии с законом Фика, во-вторых, частицы вещества, растворенного в жидкости, увлекаются последней в процессе ее движения и переносятся вместе с ней. Совокупность обоих процессов называют конвективной диффузией вещества в жидкости или газе. Исследование диффузионной кинетики растворения твердых тел в жидкости привело к установлению соотношения количества вещества, растворившегося в единицу времени, аналогичного уравнению (6.3) из работы 6. Вследствие разности концентраций растворяющегося вещества около поверхности Сs и в глубине объема возникает диффузионный слой толщиной d, являющийся основным препятствием для частиц на пути к границе раздела. По теории Нернста, распределение концентрации внутри этого слоя носит линейный характер. В слое d жидкость считается неподвижной, за пределами этого слоя она находится в движении, т.е. перемешивается, что ведет к установлению постоянной концентрации в объеме. Теория не позволяет ни вычислить d, ни оценить значение потока Y, т.е. это – качественная теория диффузионной кинетики гетерогенных взаимодействий. Позднее было доказано, что жидкость в пределах диффузионного слоя не неподвижна и распределение концентрации в нем не описывается линейным законом. Это значит, что уравнение (6.3), приведенное в работе 6, не позволяет точно вычислить скорость массопереноса. Для этого необходимо знать скорость и направление движения жидкости в пределах диффузионного слоя, а также их влияние на диффузионный перенос вещества. Наиболее простой вид имеет уравнение конвективной диффузии для реакционной поверхности в виде вращающегося диска. Анализ дает следующую картину движения жидкости около диска. При вращении диска в вязкой среде слой жидкости, непосредственно прилегающий к поверхности, вращается непосредственно вместе с ней. Наличие вязких сил вызывает вращение и более удаленных слоев, однако с удалением от поверхности вращательное движение ослабевает. Под действием центробежных сил вращающиеся слои приобретают радиальную скорость и отбрасываются к периферии. На их место подходят новые порции жидкости из глубины объема. Толщина слоя жидкости, увлекаемого во вращение (так называемого гидродинамического слоя d0), оказывается пропорциональной квадратному корню из соотношения кинематической вязкости среды n к угловой скорости вращения диска 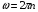 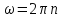 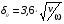 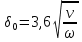 , ,где n – скорость вращения диска, об/с. Скорость W, с которой жидкость подходит к поверхности диска, определяется выражением 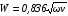 и не зависит от расстояния до оси диска. Далее анализ решений уравнения конвективной диффузии показывает, что при вращении диска всю жидкость можно разбить на две области: область постоянной концентрации во всем объеме вдали от поверхностной реакции и область быстрого изменения концентрации непосредственно вблизи этой поверхности. Последняя область представляет собой тонкий слой жидкости, в котором проявляется молекулярная диффузия. Поэтому этот слой называют диффузионным пограничным слоем d. Расчеты показывают, что в пределах слоя d концентрация раствора изменяется быстро и почти линейно с расстоянием. Тогда выражение для диффузионного потока можно представить приближенно в линейном виде: 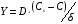 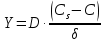 , (7.1) , (7.1)т.е. в таком виде, как и в теории Нернста. Однако в данном случае d является определенной функцией свойств жидкости и скорости ее движения, а также коэффициента диффузии: 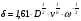 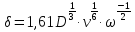 . (7.2) . (7.2)Размеры диффузионного d и гидродинамического d0 слоев связаны соотношением 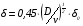 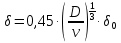 . .Из этого выражения следует, что для жидких сред толщина слоя d составляет всего несколько процентов от d0, так как 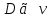 . В то же время в газах, где . В то же время в газах, где 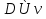 , они сравнимы по величине. , они сравнимы по величине. Толщина диффузионного слоя, как это следует из уравнения (7.2), одинакова по всей поверхности диска, что ведет к равнодоступности ее в диффузионном отношении. Наличие свойства равнодоступности выгодно выделяет поверхность вращающегося диска среди других реакционных поверхностей. Например, толщина диффузионного и гидродинамического слоев на плоской поверхности, которая смывается струей раствора, зависит от расстояния до ее переднего края, что приводит к неравномерному растворению или осаждению вещества на поверхности пластины. Зная величину d, можно по уравнению (7.1) определить поток диффундирующих частиц к поверхности диска, т.е. скорость гетерогенной реакции на диске в диффузионном режиме Y (г/см3с) 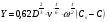 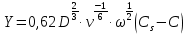 . (7.3) . (7.3)На основании экспериментальных данных о величинах Y и w, а также по взятым из справочника величинам Cs и n можно определить коэффициент диффузии вещества. Находя зависимость скорости взаимодействия от температуры, можно вычислить энергии активации скорости процесса Е и диффузии ЕD. Приведенный анализ относится к ламинарному (или безвихревому) течению жидкости вблизи вращающегося диска. Экспериментальная часть Реактивы, приборы, посуда: - металлические образцы или их соли прессованные в виде таблеток, - водные растворы кислот или растворы солей изучаемых металлов, - секундомер, - установки для изучения кинетики гетерогенных взаимодействий методом вращающегося диска (рис.7.1), - аналитические весы, - наждачная бумага. Последовательность выполнения работы. Целью данной работы является изучение кинетики растворения твердых веществ в растворах. Определение скорости растворения проводят на установке, схема которой представлена на рис. 7.1. 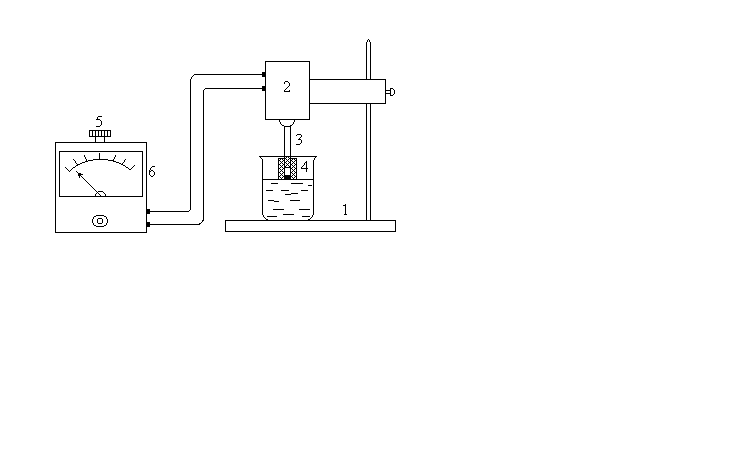 Рис. 7.1 Схема установки для изучения кинетики гетерогенных взаимодействий методом вращающегося диска Установка состоит из станины 1 с вертикальным стержнем, по которому перемещается электродвигатель 2. Электродвигатель приводит во вращение шток 3, на конце которого закреплена обойма с образцом исследуемого вещества 4. Скорость вращения образца можно плавно изменять от 0 до 1500 об/мин регулировочным устройством 5 и регистрировать при помощи стрелочного индикатора 6. Для перевода показаний индикатора в значения скорости (об/мин) используют градуировочную кривую. В работе изучают кинетику растворения металлических или прессованных из солей образцов (выдает преподаватель) в водных растворах кислот или соответствующих солей, концентрацию которых задает тоже преподаватель. Перед проведением опыта образцы, взвешенные на аналитических весах с точностью до 0,0001 г, вставляют в обойму из алюминия или фторопласта и обрабатывают наждачной бумагой с целью выравнивания торцов образца и обоймы и получения гладкой поверхности. После этого обойму навинчивают на шток, включают электродвигатель, по индикатору устанавливают одно из заданных значений скорости вращения и погружают образец в раствор на 2 – 3 мм. Одновременно с погружением включают секундомер. Время растворения (обычно 5 – 15 мин) выбирают с таким расчетом, чтобы убыль веса образца составляла не менее 0,03 г, так как малые значения Dg вызывают большие относительные погрешности при взвешивании и дальнейшем расчете Y и D. После опыта достают образец из обоймы, просушивают и повторно взвешивают. Так проводят 3 – 4 опыта при различных скоростях вращения, но одинаковых значениях времени и концентрации раствора. По данным опытов рассчитывают скорости растворения Y, используя формулу 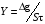 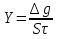 , ,где S – площадь рабочей поверхности образца. Значение коэффициента диффузии D вычисляют по формуле (7.3). Результаты измерений и расчетов заносят в табл. 7.1. Далее изучают кинетику растворения в зависимости от концентрации раствора. Для этого проводят 3-4 опыта при одном и том же значении скорости вращения диска. На основании результатов опытов строят графики: 1) 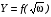 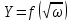 ; ;2) 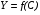 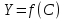 ; ;3) 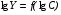 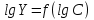 . .Таблица 7.1
Расчет поверхностных концентраций СS Считают, что если процесс растворения протекает в диффузионном режиме, то около поверхности раздела твердое – жидкость устанавливается концентрация реагентов, близкая к равновесной, т.е. соответствующая предельной растворимости данного вещества в растворителе при температуре опыта (определяют по справочнику). Исходя из значения растворимости, рассчитывают весовые доли растворяемого вещества и растворителя в приповерхностном слое раствора N1 и N2 (весовая доля – отношение массы данного компонента к массе системы (раствора)). Принимая, что плотности в этом слое (кг/см3) складываются аддитивно, с учетом весовых долей и значения плотности твердого вещества d находят концентрацию Сs: Cs = Nid. Контрольные вопросы 1. В чем отличие молекулярной и конвективной диффузии? 2. Первый и второй законы Фика. 3. Как связаны константы скоростей химической реакции и диффузии в случае, когда гетерогенный процесс идет в переходной области? 4. Почему при высоких температурах лимитирующей стадией гетерогенного процесса является диффузия? Работа №8 Изучение кинетики процессов травления полупроводников Теоретическое введение Травление – специальная обработка поверхности твердых тел с целью: а) очистки поверхности кристалла, придания ей необходимого рельефа, удаления поверхностного слоя после механической обработки. Травление применяется при изготовлении любых полупроводниковых приборов. Атомы примесей и загрязнений, находящиеся на поверхности, могут при процессе термообработки диффундировать в объем кристалла, незаметно и необратимо изменять его свойства. Кроме того, сами поверхностные загрязнения (окислы, металлические ионы, адсорбированные примеси пара воды, дефекты структуры поверхностного слоя) оказывают огромное влияние на электрофизические свойства полупроводников; б) подготовки поверхности для металлографического исследования. При этом в результате травления увеличивается оптический контраст между разнородными участками поверхности. Исследование результатов под микроскопом (металлографический метод) дает возможность определить кристаллическую структуру слитка, фазовый его состав, степень однородности. Травление рассматривают как многостадийный процесс, в него включаются следующие этапы: 1) диффузия реагента к поверхности; 2) адсорбция реагента; 3) поверхностная реакция; 4) десорбция продуктов взаимодействия; 5) диффузия продуктов реакции от поверхности. Скорость суммарного процесса зависит от наиболее медленной стадии (контролирующей). При умеренных температурах скорость травления определяется сдачей химического взаимодействия, реже – процессом диффузии. При высоких температурах контролирующей стадией служит диффузия. Адсорбция и десорбция характеризуются малыми энергиями активации, протекают (сравнительно с другими этапами) быстро и потому лишь изредка лимитируют процесс. Поверхностная реакция. Скорость взаимодействия между атомами кристалла и частицами травителя должна быть пропорциональна концентрации атомов кристалла и частиц травителя. Концентрация атомов зависит от природы материала и является величиной, постоянной для данного полупроводника. Поэтому скорость химической реакции может быть определена из соотношения 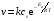 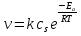 , (8.1) , (8.1)где Еа – энергия активации реакции; Т – абсолютная температура; R – универсальная газовая постоянная; сs – концентрация травителя в поверхностном слое; 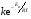 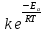 – константа скорости реакции; k – единичная скорость реакции. – константа скорости реакции; k – единичная скорость реакции.Из формулы (9.1) следует, что скорость химической реакции зависит от природы реагентов, концентрации, температуры и энергии активации. При прочих равных условиях температурная зависимость скорости реакции тем больше, чем выше Еа. Незначительное снижение Еа приводит к большим увеличениям скорости. Энергия активации зависит от структуры и состояния поверхности материала. Минимальной Еа будут обладать участки с максимальным количеством разорванных или ослабленных связей, т.е. участки, которые имеют отрицательные значения электродного потенциала. На грубо обработанных шероховатых поверхностях травление протекает с меньшей энергией активации. Так как различные кристаллографические плоскости структуры полупроводника имеют разное значение Еа, то скорость травления зависит от ориентации пластин. Посторонние атомы, дислокации и другие дефекты структуры могут повышать или понижать энергию активации растворения. Если самой медленной стадией процесса считается химическая реакция, то травители называются селективными. При селективном травлении выявляются неоднородные поверхности. Диффузия. Согласно теории Нернста диффузионный поток определяется выражением 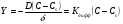 , (8.2) , (8.2)где D – коэффициент диффузии; – толщина диффузионного слоя; С и Сs – концентрации вещества в объеме и в поверхностном слое; Кдифф – единичная скорость процесса диффузии. В начальный момент времени травления С = Сs, и диффузия не происходит, условия для протекания химической реакции наиболее благоприятны. Травление селективное. Через некоторое время концентрация травителя вблизи поверхности снизится до значения Сs, скорость диффузии возрастет, а скорость реакции, наоборот, уменьшится. При достижении стационарного состояния обе скорости станут равными по величине. С этого момента Сs и скорость травления больше изменяться не будут. Диффузионный контроль наблюдается для растворов травителей с низкими концентрациями реагентов, при высоких температурах или при процессах, сопровождающихся образованием плохо растворимых продуктов. При этом скорость процесса зависит от интенсивности перемешивания, вязкости раствора и слабо зависит от температуры и структуры поверхности. Незначительное влияние температуры на скорость диффузии связано с небольшой энергией активации диффузии, составляющей всего несколько кДж/моль, в то время как энергия активации химических реакций имеет порядок десятков кДж/моль. Травители с диффузионным контролем называются полирующими. Особенность их действия заключается в сглаживании шероховатостей, нечувствительности к физическим и химическим неоднородностям поверхности. Из уравнений (8.1) и (8.2) находим выражение для Сs и подставляем его в (8.1): 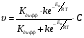 . .При условии Кдифф > kе-Еа/RT травление будет селективным, скорость процесса определяется микроструктурой данного участка (его Еа) и 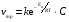 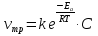 . .При условии Кдифф < kе-Еa/RT травление – полирующее, скорость процесса практически не зависит от энергии активации и 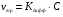 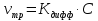 . .При механической обработке поверхности полупроводниковых материалов образуются нарушенные слои, отличающиеся по своей структуре от глубинных слоев монокристалла. Толщину нарушенного слоя можно оценить по изменению скорости травления при стадийном растворении механически обработанных образцов, поскольку механически обработанная поверхность травится быстрее, чем совершенный монокристалл. Постоянство скорости травления указывает на полное снятие нарушенного слоя. Скорость травления определяется по уменьшению толщины образца в единицу времени. Процесс определения глубины нарушенного слоя состоит из следующих этапов: 1) очистка поверхности образца; 2) взвешивание образца перед травлением; 3) удаление с поверхности в полирующем травителе тонкого слоя материала; 4) определение количества удаленного полупроводникового материала (повторное взвешивание). Этапы 2 – 4 повторяются до полного удаления нарушенного слоя (постоянство скорости травления). Экспериментальная часть Реактивы, приборы, посуда: - кремниевые пластины, - органический растворитель (толуол, изопропиловый спирт, ацетон, четыреххлористый углерод), - травители СР-8 или Уайт, - аналитические весы, - фторопластовый стакан, - стеклянные широкогорлые сосуды объёмом 100-200 мл, - пинцет с фторопластовым наконечником. Последовательность выполнения работы. Цель данной работы – изучение кинетики процессов травления полупроводников на примере кремния, определение глубины нарушенного слоя. Поверхность кремниевой пластины перед травлением обезжиривают в органическом растворителе. Обезжиривание проводится кипячением пластины в органическом растворителе или тщательной протиркой ватным тампоном, смоченным в растворителе. Затем образец взвешивают на аналитических весах с точностью до 10-4 г и определяют его площадь. Для определения глубины нарушенного слоя на кремнии используются следующие травители: СР-8 (НNO3:HF = 3:1) и Уайта (HNO3:HF = 2:1). Оба травителя являются полирующими (при использовании травителей, содержащих плавиковую кислоту, необходима фторпластовая посуда). Рис. 8.1 Кривая gi = f() Пластины кремния закрепляют во фторпластовый держатель (можно использовать пинцет с фторпластовыми наконечниками) и травят на каждом этапе по 5 – 30 с (по заданию преподавателя) при комнатной температуре. После травления образцы промывают дистиллированной водой последовательно в трех сосудах. После каждого цикла травления определяют изменение массы пластины gi. Процесс повторяют до тех пор, пока изменение массы не станет постоянным. После полного удаления нарушенного слоя строится график зависимости количества удаленного материала gi от общего времени травления . Поскольку скорость травления пропорциональна количеству удаленного материала в единицу времени, то график gi = f() характеризует изменение скорости в процессе травления. Кривая (рис. 8.1) gi = f() имеет два участка: спада и постоянства скорости травления. Зная точку перегиба, можно рассчитать глубину нарушенного слоя по формуле 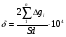 , ,где – глубина нарушенного слоя, мкм, 2gi – общее количество удаленного материала до точки перегиба на кривой, г; d – плотность исследуемого материала, г/см3, S – площадь поверхности образца, см2. Строят график gi = f(), по этому графику методом графического дифференцирования находят скорость реакции в различные моменты времени. Результаты измерений и расчетов заносят в табл. 8.1. Таблица 8.1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

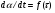 .
.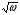 ,
,