Перевод математических текстов, знаков, символов, сокращений на английском языке - Аристова В.М.. Перевод математических текстов, знаков, символов, сокращений на. Учебнопрактическое пособие по чтению и переводу математических текстов, знаков, символов, сокращений на английском языке Калининград 1999
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
35 is “a dividend” (делимое); 5 is “a divisor” (делитель); 7 is “a quotient” (частное). Involution or Raise to power. Возведение в степень. 32, 53 are read: three to the second power or 3 squared; five cubed or 5 to the third power (to power three). x2 – x is called the “base of the power”; 2 is called “an exponent or index of the power”. Evolution. Извлечение из корня. 9 =3 is read: the square root of nine is three. 327 = 3 is read: the cube root of twenty seven is three. is called “the radical sign” or “the sign of the root”. to extract the root of … – извлекать корень из… Fractions. Дроби. Common fractions. Простые дроби. Common (simple, vulgar) fractions nowadays more often than not are written on one line: 1/2, 5 3/5, 4/7, 1/3 in printing. But there are printed works where traditional writing is used: Common fractions are read in the same way as we, Russians do, i. e.: the numerator is read as a cardinal number and the denominator as an ordinal number. If the numerator is greater than one the nominator takes the plural ending -s: 3/7 – three sevenths, 5/8 – five eighths etc. In mixed numbers the integer is read as a cardinal number and fraction must be added with “and”. E. g.: 3 2/5: three and two fifths; 10 2/7: ten and two sevenths. The reading of small fractions is often simplified: 1/2 is read a half, one half, 1/3 – a third, 1/4 – a quarter; instead of: one the second, one the third, one the fourth. Decimal fractions. Десятичные дроби. In decimal fractions the point (.) is used after the whole number in distinction from Russian, where comma (,) is used and where this sign is not read. But in Russian we must always say – десятых, сотых, тысячных и т. д., in English it is suffice to write (.) and to say “point”: 0.5 – nought [n]:t] or O [ou] point five or.5 – point five; 1.3 – one point three; 10.35 – ten point three five; 5.253 – five point two five three; 0.001 – point OO one, or point nought nought one; point two noughts one; point two Oes one. After the point (.) all numbers are read separately. Nought, O may often be omitted but the point (.) is never omitted because it shows that the number is a decimal fraction. In the USA “O” is preffered to be read as “zero”. The point (.) may be written in the upper, middle or down part of the decimal fraction: 2.5; 2·5; 2˙5. Ratio. Отношение. a: b is read: the ratio of a to b; 10: 5 is read: the ratio of ten to five; 4: 2 = 2: the ratio of four to two is two. Proportion. Пропорция. In proportion we have two equal ratios. The equality is expressed by the sign:: which may be substituted by the international sign of equality =. a: b:: c: d or a: b = c: d – is read: a is to b as c is to d; 2: 3:: 4: 6 or 2: 3 = 4: 6 – is read: two is to three as four is to six. The extreme terms of proportion are called “extremes”, the mean terms are called “means”. The proportion can vary directly (изменяться прямо пропорционально) and it can vary inversely (изменяться обратно пропорционально): x (y: x varies directly as y; x is directly proportional to y; x = k/y: x varies inversely as y; x is inversely proportional to y. Equations and Identities. Уравненияитождества. There are different kinds of equations. In general the equation is an equality with one or several unknown variable(s). The reading of equations is the same as in Russian: 30 + 15 + x2 + x3 = 90 – is read: thirty plus fifteen plus x squared plus x cubed is equal to ninety. 2 + b + 6 + b4 = 160 – is read: two plus b plus the sqare root of six plus b to the fourth power is equal one hundred and sixty. The identity is an equality, valid at all admissable values of its variables. The identities are read: a + b = b + a – a plus b equals b plus a; sin2x + cos2x = 1 – sine squared x plus cosine squared x is equal to one. Arithmetical and Geometrical Progressions. Арифметическая и геометрическая прогрессии. An arithmetical progression is a sequence such as 3, 5, 7, 9 …, in which each member differs from the one in front of it by the same amount. A geometrical progression is a sequence such as 3, 6, 12, 24 …, in which each member differs from the one in the same ratio. “The number of families holidaying abroad grew now in geometrical progression”. Mathematicians more often use now the expressions arithmetic sequence and geometric sequence. Reading formulae. Чтение формул. |
| a (b = c | a divided by b is equal to c |
| 2 (2 = 4 | twice two is four |
| c (d = b | c multiplied by d equals b |
| dx | differential of x |
| | a plus b over a minus b is equal to c plus d over c minus d |
| ya-b · xb-c = 0 | y sub a minus b multiplied by x sub b minus c is equal to zero |
| | the second derivative of y with respect to s plus y times open bracket one plus b of s in parentheses, close bracket is equal to zero |
| (x) dx | the integral of (x) with respect to x |
| b (x) dx a | the definite integral of (x)with respect to x from a to b (between limits a and b) |
| c(s)= Kab | c of s is equal to K sub ab |
| xa-b = c | x sub a minus b is equal to c |
| a (b | a varies directly as b |
| a: b:: c: d; a: b = c: d | a is to b as (equals) c is to d |
| x (6 = 42 | x times six is forty two; x multiplied by six is forty two |
| 10 (2 = 5 | ten divided by two is equal to five; ten over two is five |
| | a squared over c equals b |
| a5 = c | a raised to the fifth power is c; a to the fifth degree is equal to c |
| | a plus b over a minus b is equal to c |
| a3 = logcb | a cubed is equal to the logarithm of b to the base c |
| logab = c | the logarithm of b to the base a is equal to c |
| xa-b = c | x sub a minus b is equal to c |
| | the second partial derivative of u with respect to t equals zero |
| c: d = e: l | c is to d as e is to l |
| 15: 3 = 45: 9 | fifteen is to three as forty five is to nine; the ratio of fifteen to three is equal to the ratio of forty five to nine |
| p Т | p is approximately equal to the sum of x sub i delta x sub i and it changes from zero to n minus one |
| a2+b2 - a2+b12 #b - b1 | the square root of a squared plus b squared minus the square root of a squared plus b sub one squared by absolute value is less or equal to b minus b sub one by absolute value (by modulus) |
| lim azn azn # n | a to the power z sub n is less or equal to the limit a to the power z sub n where n tends (approaches) the infinity |
| | The sum of n terms a sub j, where j runs from 1 to n |
| 481 = 3 | The fourth root of 81 is equal to three |
| c (d | c varies directly as d |
| sin (= a | Sine angle (is equal to a |
| | Integral of dx divided by (over) the square root out of a square minus x square |
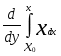 | d over dx of the integral from x sub 0 to x of capital xdx |
Addenda. Приложение.
Latin / Greek singular and plural forms of some mathematical terms.
Латинские / греческие формы единственного и множественного числа
некоторых математических терминов.
| ед. ч. sing. | мн. ч. plur. | | |
| - is [ws] | - es [w:z] | axis - axes analysis - analyses hypothesis - hypotheses parenthesis - parentheses thesis - theses basis - bases | ось - оси анализ - анализы гипотеза - гипотезы скобка-скобки тезис, диссертация - тезисы, диссертации база, основание - базы, основания, |
| - a [c] | - ae [aw] | formula - formulae lamina - laminae | формула - формулы тонкая пластинка - тонкие пластинки |
| - us [cs] | - i [aw] | syllabus - syllabi locus - loci [lousaw] nucleus - nuclei radius - radii focus - foci modulus - moduli genius - genii; geniuses stimulus - stimuli | программа - программы геом.: место точек, траектория - траектории ядро - ядра радиус - радиусы фокус - фокусы модуль - модули гений - гении; демон - демоны стимул - стимулы |
| - on [n] | - a [c] | criterion - criteria phenomenon - phenomena polyhedron - polyhedra | критерий - критерии явление - явления многогранник - многогранники |
| -um [m] | - a [c] | datum - data momentum - momenta quantum - quanta maximum - maxima minimum - minima erratum - errata symposium - symposia spectrum - spectra medium - media corrigendum - corrigenda | данное - данные момент - моменты квант - кванты максимум - максимумы минимум - минимумы ошибка - ошибки симпозиум - симпозиумы спектр - спектры середина - середины опечатка, поправка - опечатки, поправки |
| - х [ks] | - ces [sw:z] | matrix - matrices radix - radices vertex - vertices index - indeces appendix - appendices helix - helices | матрица - матрицы основание, корень - корни вершина - вершины показатель - показатели приложение - приложения спираль - спирали |
Reading Proper Names. Чтение собственных имен.
| Alexander J. W. | [Flwg ‘zandc] | Александер, Джеймс | 1888-1971 |
| Ampere A. M. | [ ‘ Fmpec] | Ампер А.М. | 1775-1836 |
| Abel N. | [ewbl], [:bcl] | Абель Н. | 1802-1829 |
| Archimedes | [:kw ‘mwdwz] | Архимед | 287-212 BC |
| Avogadro A. | [Fvc ‘ga:drou] | Авогадро А. | 1776-1856 |
| Aristotle | [ ‘Frwst]tl] | Аристотель | 384-322 BC |
| Bardeen J. | [b: ‘dw:n] | Бардин, Джон | 1908- |
| Bessel F.T. | [‘ bescl] | Бессель, Фридрих | 1784-1846 |
| Bolyai J. | [b]lew] | Бойаи (Больяй) Янош | 1802-1860 |
| Berkley J. | [b:klw] | Беркли Дж. | 1685-1753 |
| Bernoulli J. | [bc:nu:lw] | Бернулли Я. | 1654-1705 |
| Brewster, Sir David | [bru:stc] | Брустер, сэр Дэвид | 1781-1868 |
| Cauchy A.L. | [k]:•w] | Коши, Огюстен | 1789-1857 |
| Clifford W.S. | [‘klwfcd] | Клиффорд, Уильям | 1845-1879 |
| Copernicus N. | [kou ‘pc:nwkcs] | Коперник Н. | 1473-1543 |
| Coulomb Ch. | [‘ku:l]:m] | Кулон, Шарль | 1736-1806 |
| Crelle A.L. | [‘krelc] | Крелль Август | 1780-1855 |
| Curie M. | [kju: ‘rw:] | Кюри, Мария | 1867-1934 |
| Davy H. | [dewvw] | Деви Х. | 1778-1829 |
| De Broglie L. | [dc ‘br]wlw] | Бройль (де Бройль) Л. | 1892-1958 |
| Dedekind Y.W. | [‘dedckwnd] | Дедекинд Юлиус | 1831-1916 |
| Demokritus | [dw ‘m]krctcs] | Демокрит | .470 BC |
| Descartes R. | [dew ‘k:t] | Декарт Р. | 1596-1650 |
| Diophantes | [daw] ‘fentcs] | Диофант | III в. |
| Dirac P. | [dw ‘rFk] | Дирак П. | 1902 |
| Dirichlet P.G. | [dwrwk ‘le] | Дирихле Петер | 1805-1859 |
| Einstein A. | [‘awnstawn] | Эйнштейн А. | 1879-1955 |
| Eisenstein F.M. | [,awzcn ‘stawn] | Эйзенштейн Ф. | 1823-1852 |
| Empedocles | [em ‘pedcklw:z] | Эмпедокл | 490-430 BC |
| Epicurus | [epw ‘kjucrcs] | Эпикур | 341-270 BC |
| Eudoxus | [ju: ‘d]kscs] | Евдокс | 408-355 BC |
| Euclid | [ju:klwd] | Эвклид, Евклид | III в. BC |
| Euler L. | [ ‘]wlcr, ]wlc] | Эйлер Л. | 1707-1783 |
| Fahrenheit G. | [‘ fFrcnhawt] | Фаренгейт М. | 1686-1736 |
| Faraday M. | [‘ fFrcdw] | Фарадей М. | 1791-1867 |
| Fermat P. | [,fc ‘m:, ferm:] | Фермб, Пьер | 1601-1665 |
| Fermi E. | [,fc ‘mw:, fermw:] | Ферми Э. | 1901-1954 |
| Foucault | [fu:kou] | Фуко | 1819-1868 |
| Fourier J.B. | [fu ‘rwc:] | Фурье Ж.Б. | 1768-1830 |
| Galilei G. | [‘ gFlwlw] | Галилей Г. | 1564-1642 |
| Gauss C. | [g:us; gFus] | Гаусс К. | 1777-1855 |
| Galois E. | [gclu ‘:] | Галуа, Эварист | 1811-1832 |
| Geiger H. | [gwgc] | Гейгер Х. | 1882-1945 |
| Germain | [Ґer ‘mc:n] | Жермен Софи | 1776-1831 |
| Gielbert W. | [‘ gwlbct] | Гильберт У. | 1544-1603 |
| Gцdel K. | [gc:dcl] | Гёдель К. | 1906-1978 |
| Gregory J. | [‘ gregcrw] | Грегори Дж. | 1638-1678 |
| Hamilton W.R. | [‘ hFmwltcn] | Гамильтон, Уильям | 1805-1865 |
| Hilbert D. | [‘hwlbct] | Гильберт Д. | 1862-1943 |
| Heisenberg V. | [‘hwznbc:g] | Гейзенберг В. | 1901-1976 |
| Hippocrates | [hw ‘p]krctw:z] | Гиппократ | V в. BC |
| Huygens E. | [‘ hwgenz] | Гюйгенс Э. | 1629-1695 |
| Joule J. | [®u:l] | Джоуль Дж. | 1818-1889 |
| Kelvin W. | [‘ kelvcn] | Кельвин, Томсон У. | 1824-1907 |
| Khayyam Omar | [kw ‘jam ‘oum:] | Хайям Омар | 1048-1123 |
| Lagrange J.L. | [lc ‘gr:nҐ] | Лагранж Жозеф | 1736-1813 |
| Laplace P.S. | [lc ‘pl:s] | Лаплас Пьер | 1749-1827 |
| Legendre A.M. | [lc ‘Ґ:nr] | Лежандр Адриен | 1752-1833 |
| Leibniz G.W. | [lwbnwz] | Лейбниц Готфрид | 1646-1716 |
| Lucretius | [lu: ‘krw:•cs] | Лукреций | I B.C. |
| Maclaurin | [mck ‘l]:rwn] | Маклорен К. | 1698-1748 |
| Maxwell J.C. | [mFkswcl] | Максвелл Дж. | 1831-1879 |
| Mercater G. | [mc ‘kewtc] | Меркатор Герард | 1512-1594 |
| Monge G. | [m]:nҐ] | Монж Гаспар | 1746-1818 |
| Napier J. | [‘ newpwc, nc ‘pwc] | Непер Дж. | 1550-1617 |
| Piazzi G. | [pw ‘:scw] | Пиацци Джузеппе | 1746-1826 |
| Picard E. | [pw ‘k:] | Пикард Эмиль | 1856-1941 |
| Plato | [ ‘plewtou] | Платон | 428-348 BC |
| Poincare J.H. | [‘ pw:nkare] | Пуанкаре Ж.А. | 1854-1912 |
| Ptolemy Claudius | [‘t]lwmw kl]:djcs] | Птолемей Клавдий | -9-160 AD |
| Pythagoras | [paw ‘›Fgcrcs] | Пифагор | 570-500 AD |
| Pythogorean | [paw,›Fgc ‘rw:cn] | пифагорийский | |
| Ramanujan S. | [rc,mcnc ‘®en] | Рамганужан Ш. | 1887-1920 |
| Riemann B. | [‘ rw:mcn] | Риман Б. | 1826-1866 |
| Saccheri Girolamo | [sc ‘±erw ®wrc ‘lewmou] | Саккери Джароламо | 1667-1733 |
| Simpson T. | [swmpsn] | Симпсон Т. | 1710-1761 |
| Socrates | [s]krctw:z, souk…] | Сократ | 470-399 BC |
| Syracuse | [‘ sawcrckju:z] | Сиракузы | |
| Taylor B. | [tewlc] | Тейлор Б. | 1685-1731 |
| Torricelli | [t]rw ‘±elw] | Торричелли | 1608-1647 |
| Thales | [›ewlw:z] | Фалес Милетский | 624-548 BC |
| Wiener N. | [ww:nc] | Винер Норберт | 1894-1964 |
| Weierstrass K. | [‘ wawcstrcs] | Вейерштрасс Карл | 1815-1897 |
It is interesting to know
1. Pythagoras of Samoss (570-500 BC) opened a philosophy school where a number was considered as being the «essence» of all things and the Universe – as harmonic system of numbers and their relations with each other.
Pythagoreans distributed all numbers into classes: even and odd, prime and compound, perfect, friendly, harmonic, triangle, guadratic and pentagonal etc. Figure «one» was assumed to be deity, reason, good, harmony, luck. Figures “1”,”2”,”3”,”4” were taken as fundamental, “5” was the symbol of a happy unit (marriage) because it was the sum of the first even and odd numbers (excluding 1 as the basis of all numbers). “6” was the symbol of soul, as it was the first perfect number and its divisors’ sum (1+2+3) was equal to the number itself. Figure “7” sumbolyzed health and “8” was the symbol of love and friendship.
Number “36” embodies the whole world that surrounded us, because 36 presented the sum of the first even (2+4+6+8) and the first odd (1+3+5+7) numbers and that these figures constituted the Universe.
2. Geometry emerged in Egypt where the peasants had to measure land plots, whose borders were washed away by the Nile’s over-flows.
3. Geometry as a science appeared in Greece after the Egyptian practical notions in geometry had penetrated there. Greek scientists and philosophers such as Thales, Democritus, Pythagoras, Euclid developed geometry into a strict harmonious mathematical theory.
4. Every proved theorem in geometry serves as an axiom in subsequent proofs.
5. The word “algebra” originated in Arabian language (aljebr) and it meant – “reunion of broken parts” – воссоздание, воссоединение разрозненных частей.
6. Omar Khayym, the famous Eastern poet, philosopher, astronomer and mathematician considered algebra to be “the scientific art”.
Omar Khayym’s mathematical calculations in composing Calendar were taken into account by the French to compile the revolutionary calendar in the late XVIII century.
7. It was Democritus who was the first to compute infinitesimal quantities.
8. One metre was chosen as an International standard in measuring linear segment units as a measure almost equal to 1/40,000,000 th part of the terrestrial meridian.
9. P.Fermat (1601-1665) was a lawer, mathematics being his hobby. But he became famous due to mathematics. He is considered to be the founder of Analitical geometry and Theory of Numbers.
10. Fermat’s theorem (or Great Theorem), which postulates: “there do not exist three whole numbers x, y, z where the equality xn+yn=zn would be implemented if n 2” has not been proved in its general form up till now.
11. The formula to define the Sunday when the Ortodox Easter comes according to the Gregorian Calendar was introduced by an outstanding German mathematician Gauss K.F. (1777-1855). His formula works and is valid for the past, present and future.
12. The greater early painters Raphael, Michelangelo, Leonardo da Vinci based their works on geometric principles.
13. Sculpture, architecture, painting are all based on using geometric forms and proportions and even in ancient times they were taken into account in determing the proportions of famous buildings: the Parthenon, the Acropolis in Athens, triumphal arches and Gothic cathedrals.
14. Euclid’s “Elements”, wriiten more than 2000 years ago is still used in Great Britain as a textbook on geometry.
15. Gödel K. – an Austrian-born (1906-1978) famous USA logician and mathematician presented a page of symbols that purports to be a rigorous proof for the existence of God. This latter is a recasting of the notorious “Ontological Argument” for God’s existence into the language of mathematical logic. He established first the “theorem” – M(x) G(x) (N (y) G (y) – which says that, if God’s existence is possible, then it is necessary, and then argues that God’s existence is indeed possible. Therefore, necessarily, God exists.
16. Rene Decartes, the famous mathematician (1596-1650) did not accept imaginary numbers and it was not surprising that he flatly rejected them in his mathematical investigations.
17. Galileo once remarked, that the great book of nature is written in the language of mathematics.
18. The first Russian woman-mathematician S.Kovalevskaya became famous not in Russia but in Göttingen University where she had supported for her Doctoral thesis.
19. The word “cybernetics” appeared in American English in 1946. This word was coined by the founder of cybernetics Norbert Wiener (1894-1964) from two Greek blends and it meant «наука управления». This word had existed in Plato’s work – Dialogues, but its meaning had been “the art of navigation”.
20. Almost all terms connected with cybernetics and computing technique in Russian are of English origin because cybernetics was not admitted as science in the Soviet Union during many years and when at last it was recognized all the terms were taken-ready by the Russian language of this branch of science.
21. The first woman president of the American Economic Association is now in office (1996). Joan Robinson of Cambridge University was acknowledged as one the great 20-th century economists even by her (male) enemies. Brady and Schwartz can be counted as founders of quantitative economic history. But in general famous women in mathematics and economy are rare and it is explained by the fact (in the previous ages and later up till 1960) of the then existing misogyny [maw ‘s]®wnw] in sciences. This trend got the title “Great American Gender Reaction” in the USA.
22. Professor Garrow (London) said that the modern ideal woman favoured by clothes designers and fashion editors was physiologically underweight.”Models with a BMI of less than 18 are thinner than it is healthy to be”. BMI (Body-Mass-Index) is calculated by measuring weight against height: kilograms divided by metres squared – kg/m2. A woman 5 ft 8 in. tall weighing 11 stone has a BMI of 23.3. Every woman of that height with a weight from just under 9 stone to just over 12 stone would fall within the normal BMI range of 20 to 25. Professor Garrow said: “If your BMI is between 20 and 25 for God’s sake worry about something else, not your weight”.
23. Hilbert David, a great German mathematician was born in Königsberg in 1862. He was the first to reduce geometry to a series of axioms and to contribute substantially to the establishment of the formalistic foundations of mathematics. Due to these foundations the development of mathematics and logic after Hilbert was different from the previous one. The city of Königsberg in 1930 made Hilbert an honorary citizen. Hilbert is known to be one of the greatest and most versatile mathematicians of his time.
24. Jules Henri Poincare the prominent French mathematician, astronomer and philosopher of science emphasized the subconscious, while probing the psychology of mathematical discovery and invention. He was a forerunner of the modern intuitionist school and he believed, that sudden illumination, following long subconscious work, was a prelude to mathematical creation.
25. Norbert Wiener, the founder of cybernetics, wrote that Cholmogorov’s thoughts were the same as his ideas and he knew that Cholmogorov had independently analysed some principal questions in mathematics connected with cybernetics and had been the first to publish the results. Weiner also mentioned many Russian mathematicians in his books with the only aim – to attract attention to his new ideas. But he could not imagine the impression and exitation his ideas had made upon the scientists all over the world!
26. John Leslie, a professor of philosophy tried to estimate the probabilities of the end of the world, the Apocalypse. His list is rather sobering: Risks already well recognized: 1. Nuclear war. 2. Biological warfare. 3. Chemical warfare. 4. Destruction of the ozone layer. 5. Greenhouse effect. 6. Poisoning by pollution. 7. Disease. Risks often unrecognized – Group First: Natural disasters – 1. Volcanic eruptions. 2. Hits by asteroids and comets. 3. Extreme ice age due to passage through an interstellar cloud. 4.Nearby supernova. 5. Other massive astronomical explosions. 6. Essentially unpredictable breakdown of a complex system. 7. Something-we-know-not-what. Group Two: Manmade disasters: 1. Unwillingness to rear children. 2. Disaster from genetic engineering. 3. Disaster from nanotechnology. 4. Disasters connected with computers. 5. Disaster from some other branch of technology, perhaps just agricultural which had become crucial to human survival. 6. Production of a new big bang in the laboratory. 7. Possible production of an alldestroying phase transition. 8. Annihilation by extraterrestrials. 9. Something-we-know-not-what. Risks from philosophy. These include: threats associated with religions; Schopenhauerian pessimism; negative utilitarianism; and the prisoner’s dilema (The Times Higher, 13.09.1996.).
27. Benjamin Franklin (1706-1790) an outstanding American politician and scientist was the first to introduce the terms “plus”, “minus”, “positive”, “negative” electricity. He invented devices known as “battery” and “lightening-rod”.
List of terms and expressions.
The list given below consists of words and expressions difficult for translating from English into Russian and vice versa.
Sometimes they are words familiar with commonly used ones (leg – нога; belief – вера; biased – предубежденный; both – оба, etc.) or words with terminological meanings (artificial numbers – логарифмы) or prepositions, adverbs or phraseological units where the students and post-graduates make bad mistakes.
| A one, A1 | первоклассный |
| according to | в соответствии |
| adjoining leg | прилежащий катет |
| all the more | тем более |
| all the same | все равно |
| all one | все равно |
| angular minute | угловая минута |
| alternate angles | накрест лежащие углы |
| artificial numbers | логарифмы |
| as if, as though | как будто, как если бы |
| as it were | как бы; так сказать |
| as of (1945) | по данным на 1945 г. |
| as often as not | нередко |
| (in) as much as | поскольку, ввиду того, что |
| as per | согласно |
| as-proved | в том виде как доказано |
| at any rate | по крайней мере |
| at randon | наугад |
| backward difference | разность назад |
| bank of a cut | граница разрeза |
| be of value (importance) | иметь значение |
| bear in mind | хранить в уме, помнить |
| because of | из-за, вследствие, поскольку |
| belief line | доверительная вероятностть |
| be soluble | являться, быть разрешимой |
| beyond he is beyond me at the far of beyond | вне, за он знает больше меня у черта на куличках |
| biased estimate | оценка смещения |
| both … and | как … так и |
| break point | точка излома |
| broken brackets | угловые скобки |
| by means of | посредством, при помощи |
| by no means | никоим образом |
| case in hand | рассматриваемый случай |
| in case | если |
| in the case of | в случае |
| in any case | во всяком случае |
| the case is | дело в том, что |
| in no case | ни в коем случае |
| cardinal (number), power | кардинальное число; мощность множества |
| centesimal minute | минута метрическая (угла) |
| close second | почти первый (в чем-либо) |
| computer oriented | связанный с компьютером |
| continuous mapping | непрерывный оператор |
| contracting mapping theorem | принцип сжимающих отображений |
| convert into | превращать в … |
| convex programming | выпуклое программирование |
| coprime numbers | взаимно, попарно простые числа |
| crash problem | срочная программа |
| cusp, caspidal point | точка возврата |
| dashed, dotted line | пунктирная линия -----,..... |
| debug the system | убрать ошибки из системы (комп.) |
| decimal a repeating d. | десятичная дробь периодическая дробь |
| depend on, upon | зависеть от |
| due | во-время, должный |
| due to | благодаря (чему-то, кому-то), вследствие |
| dwell upon, on | остановиться (на чем-то), рассказать |
| essence The very essence | суть, истина истинная суть |
| even number | четное число |
| even money | круглая сумма |
| evenly even unevenly even | кратный четырем кратный двум, но не кратный четырем |
| even so | даже, если это так |
| even though | даже, если |
| ever increasing if ever hardly ever | все возрастающий если это может быть вообще редко, почти никогда, едва ли |
| fly off at a tangent | отойти от главного, от темы |
| far cry | большое расстояние, большая разница |
| far from | далеко не … |
| few and far | мало и редко |
| first things first | сначала главное |
| for | так как |
| for all that | несмотря на это |
| for granted | без доказательства |
| for one | например |
| for once | на этот раз, однажды |
| for the sake | ради (чего-либо) |
| gem of arithmetic | жемчужина математики, «золотая теорема» |
| generalities | общие замечания |
| generally recognized | общепризнанный |
| get rid of | избежать (чего-то), отделаться |
| granting, granted | допустим, что … |
| half as high | в два раза ниже |
| half as large / much | в два раза меньше |
| hard | много, усиленно (что-то делать); трудный, тяжелый |
| hardly | едва; еле-еле; вряд ли |
| to have nothing to do | не иметь ничего общего |
| highlight | основной факт, момент |
| if and only if | тогда и только тогда |
| if any, if at all, if ever, if so | если вообще (имеет место) если да; если так |
| in any case | во всяком случае |
| inasmuch | поскольку; ввиду того, что |
| in order to / for | для того, чтобы |
| in question | рассматриваемый, исследуемый |
| in terms of | в смысле, при условии, за счет, в каких-то единицах; в понятиях; в плане; в виде; на основе |
| know-how | справочник, опыт, инструкция |
| last but one | предпоследний |
| let alone | не говоря уже о … |
| (as) little as | только, до (перед цифрами) |
| likelihood function | функция (правдоподобная, правдоподобия) |
| Möbius band, strip | лист Мёбиуса |
| make sense | иметь смысл |
| make a report | сделать доклад |
| malfunction | искажать; неисправность |
| marginal concept | решающая концепция |
| more often than not | нередко |
| (the) more so | тем более, что |
| moreover | кроме того, более того |
| most directly | сразу |
| most probably | вероятнее всего |
| neither... nor | ни … ни |
| no longer | больше не … |
| nodal singularity, knot | узел |
| not at all | нисколько, вовсе нет |
| non-intersecting sets | непересекающиеся множества |
| n-taple root | n-кратный корень |
| null and void | недействительный, аннулированный |
| a number of | немного, несколько, некоторые |
| the numbers of | масса, много |
| in numbers | в большом количестве |
| “Number “3”, “8”, “13”” | (жарг.) названия наркотиков |
| (Smb’s) number is up | чья-то песенка спета, ему крышка |
| Number of the beast | (библ.) 666 - число зверя |
| odd | нечетный, лишний, добавочный, случайный |
| odds | неравенство, излишки |
| on account of | вследствие, из-за |
| on no account | ни в коем случае |
| only | только |
| the only | единственный |
| on the one / other hand | с одной / другой стороны |
| opinions differ | мнения расходятся; о вкусах не спорят |
| other than | кроме |
| owing to | из-за, в связи с, благодаря |
| over the range | в диапазоне, в пределах |
| out of order | в беспорядке |
| pagoda | запись |
| par excellence | преимущественно |
| partial equation | уравнение в частных производных |
| pay attention to | обратить внимание на … |
| place the limit | установить предел |
| place over | помещать над … (чертой, буквой) |
| put forward | выдвинуть (теорию) |
| proceed from | исходить из |
| to | приступать к |
| proceedings | труды (ученого общества), протоколы, записки |
| put into practice | вводить в практику |
| question to beg the question in question out of the question | вопрос считать вопрос решенным искомый, рассматриваемый не может быть и речи |
| raise to the power | возводить в степень |
| ranging from... to | в пределах от … до |
| reasoning from this | исходя из этого, рассуждая по поводу |
| regarding / regardless | относительно / независимо от |
| result | происходить в результате |
| result in | иметь в результате |
| result from | быть следствием от |
| Roentgen rays [‘ r]ntjcn] | Х-лучи, рентгеновские лучи |
| root mean square | среднеквадратичное значение |
| running | подряд |
| sampled | дискретный |
| save and except; save for | за исключением, не считая |
| scale down | сводить к одному / определенному масштабу |
| score(s) | счет; множество; два десятка |
| seeing | поскольку |
| set up | учредить |
| aside | отложить, не учитывать |
| forth | выдвигать, излагать |
| to | приступать |
| singlevalued | однозначный |
| short cuts | правила делимости |
| so much as | столько, как; даже |
| so much so | до такой степени; так, что |
| solid line | сплошная линия |
| solid angle | телесный угол |
| subject matter | основная тема, предмет обсуждения |
| subject to | в соответствии; допуская, если |
| tаkе for granted | считать доказанным, принимать без доказательства |
| take into account | принимать в расчет |
| take place | иметь место, происходить |
| take the floor | взять слово, иметь слово |
| thanks to | вследствие |
| that is why | вот почему |
| theorema aureum (лат.) | «золотая теорема» |
| the... the | чем …, тем |
| thereby | тем самым |
| therein | в нем, в ней, там |
| thus far | до сих пор, пока |
| three times | умноженный на 3, в три раза больше, трижды |
| thrice | трижды |
| to a lesser extent | в меньшей степени |
| twice as good | вдвое лучше |
| twice as little | вдвое меньше |
| twice as much / large | вдвое больше |
| two by four | 2×4; мелкий, незначительный |
| in two twos | в два счета, немедленно |
| two upon ten | смотри в оба, чтобы (10 пальцев) не взяли (украли) |
| to be explicit | чтобы было яснее, понятнее |
| under way | в работе; осуществляемый сейчас |
| unequivocal | определенный |
| unlikely | маловероятно |
| unlooped | несамопересекающаяся (прямая) |
| untenable | несостоятельный |
| vain; in vain | напрасный, напрасно, тщетно |
| valid | действительный, правильный |
| value | значение; величина |
| vanish | стремиться к нулю |
| variety of | целый ряд, множество (чего-то) |
| virtue by (in) virtue of | свойство посредством, в силу чего-то |
| wake in the wake of | след, кильватер вслед за (кем то) |
| want | недостаток, отсутствие, необходимость |
| for want of | из-за отсутствия |
| way by way of either way round in a way in a rough way in no way the other way (round) | путь, способ; образ действия с целью, через, посредством любым путем до некоторой степени приблизительно, при грубом подсчете никоим образом иначе (наоборот) |
| well well above / over as well (as) | вполне, значительно, как раз значительно выше, больше также и; также как и |
| whatsoever | вообще, совсем |
| whence | откуда |
| whereby | тем самым, посредством чего |
| whether... or | или … или; независимо от |
| whether it be | будь то |
| yet as yet not yet | еще, все еще; тем не менее, однако все еще, пока еще не |
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Англо-русский политехнический словарь / Под ред. А.Е.Чернухина. М., 1971.
2. Малаховский В.С. Введение в математику. Калининград: Янтарный сказ, 1998.
3. Никифоровский В.А. В мире уравнений. М.: Наука, 1969.
4. Орлов В.Б., Скороход Н.С., Сосинский А.Б. Русско-англо-немецко-французский математический словарь. М., 1987.
5. Пекелис В. Кибернетическая смесь. М.: Знание, 1982.
6. Словарь-минимум для чтения научной литературы на английском языке. М.: Наука, 1969.
7. Collins Double Book. Dictionary and Encyclopedia. - London & Glasgow, Collins, 1974.
8. Concise Oxford Dictionary of Current English. IV ed., Oxford Univ. Press, 1956.
9. Daintith J et al. The Oxford Minidictionary of Abbreviations. - Oxford Univ. Press - New York, 1993.
10. Hornby A.S. et al. - Oxford Advanced Learner’s Dictionary of Current English. - Vol. I,II. - Oxford Univ. Press - Oxford, 1982.
11. Greenbaum S., Whitcut J. - Guide to English Usage. - Longman Group UK Limited, 1988.
12. English newspapers: The Times; The Times. Higher Education; The Financial Times, 1996-1998.
1 The data are taken from English-Russian Polytechnical Dictionary. - M., 1971; Orlov V.B. at al. Russian -English - German - French Mathematical Dictionary. - M., 1987.
2 'quid' is a slang word for "pound of sterling". It is used only in a singular form: He earns fifty quid a week = Ј 50 в неделю.
3 This slang word is supposed to have come into American English from the Nothern American-Indian language where it meant buckskin — оленья шкура, кожа; which had been used as a unit of barter at that time.
Here the most widely used measures are included.
