Метрология. Учебное пособие. 2006 г. Введение 2 Глава измерение физических величин 4 Объекты измерений 4
 Скачать 1.42 Mb.
|
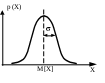
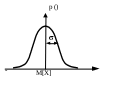
1.3. Погрешности измеренийРезультат измерений величины зависит от многих факторов: выбора метода и средства измерений, условий его осуществления (например, температуры, давления, влажности окружающей среды), способа обработки результатов измерений, квалификации оператора, выполняющего измерения, и др. Указанные факторы приводят к различию в значении результата измерения величины и ее истинного значения, т.е. к погрешности. Одной из основных задач метрологии является разработка методов определения погрешностей измерений. В зависимости от степени приближения к объективно существующему значению величины следует различать истинное значение величины и результат ее измерения, а также ее действительное значение. Истинным значением Хи величиныназывают значение, идеальным образом характеризующее в качественном и количественном отношении соответствующую физическую величину. Оно может быть получено только в результате бесконечного процесса измерений с бесконечным совершенствованием методов и средств измерений. Результатом измерения Хизм называют значение, полученное при ее измерении с применением конкретных методов и средств измерений. Погрешность результата измерения (или погрешность измерения) – это отклонение результата измерения от истинного значения измеряемой величины, т.е. = Хизм – Хи. Но поскольку истинное значение измеряемой величины неизвестно, то точно неизвестны и погрешности измерений, поэтому на практике для определения погрешности используют так называемое действительное значение величины, которым заменяют истинное значение. Действительное значение Хдвеличины – это значение, полученное экспериментально и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него. Действительное значение находят более точными методами и средствами измерений. Чем выше точность средства и метода измерений, с помощью которых определено Хд, тем с большей уверенностью оно рассматривается как близкое к истинному. Поэтому на практике погрешность измерения (здесь имеется в виду абсолютная погрешность) находят по формуле = Хизм – Хд (1.6) Полностью устранить погрешности невозможно, но можно уменьшить их с помощью методов, рассмотренных ниже. Точность результата измерения – это одна из важнейших характеристик (показателей) качества измерения, отражающая близость к нулю погрешности результата измерения. Кроме того, показателями качества измерений являются сходимость, воспроизводимость, правильность и достоверность результатов измерений, о которых речь пойдет ниже. Классификация погрешностей измеренийНа рис. 1.7 приведена классификация погрешностей измерений с указанием основных признаков.  Рис. 1.7. Классификация погрешностей измерений При осуществлении процесса измерения (рис. 1.2), на его результат влияют работа средства измерения, правильность методики, приемы работы оператора, влияющие величины и др. Поэтому погрешность измерения может включать инструментальную си, методическую м, субъективную погрешности суб, а также погрешности из-за изменений условий измерения усл, т.е. = си + м + суб + усл (1.7) Инструментальная погрешность обусловлена погрешностью применяемого средства измерения. К основным причинам ее возникновения относят - несовершенство конструкции (схемы) средства измерения; - несовершенство технологии изготовления средства измерения; - помехи на входе средства измерения, вызываемые его подключением к объекту измерения; - постепенный износ и старение материалов, из которых средства измерений изготовлены. Инструментальная погрешность, как правило, является одной из наиболее ощутимых составляющих погрешности результата измерения. Погрешность метода (методическая) погрешность обусловлена несовершенством принятого метода измерений, недостаточной изученностью явления, положенного в основу измерения. Субъективная погрешность измерения обусловлена индивидуальными особенностями оператора (например, погрешностью отсчета оператором по шкале прибора). Они, как правило, вызваны невнимательностью оператора, закрепившимися у него неправильными приемами работы, несовершенством его органов чувств, недостаточной подготовленностью. При использовании автоматизированных средств измерений эти погрешности отсутствуют. Погрешность из-за изменений условий измерения возникает вследствие недостаточно учтенного действия той или иной влияющей величины (температуры, влажности, атмосферного давления, вибрации и др.), а также неправильной установки средств измерений или нарушения правил их взаимного расположения. Например, если прибор должен быть установлен в вертикальном рабочем положении, то его использование в горизонтальном положении приведет к погрешности. По закономерности проявления погрешности результата измерения подразделяют на две группы: случайные и систематические погрешности. Случайная погрешность  – это составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью одной и той же величины.Эта погрешность возникает вследствие множества причин: вариации показаний средства измерения, погрешности округления при отсчете показаний, изменений условий измерения случайным образом и др. Случайные погрешности обнаруживают при повторных измерениях одной и той же величины в виде некоторого разброса (расхождений) получаемых результатов. Причинами расхождений значений результатов измерений могут оказаться и случайные изменения самой измеряемой величины. Уловить и провести грань между случайными погрешностями процесса измерения и случайными изменениями самой измеряемой величины в большинстве случаев практически невозможно. В каждом опыте причины расхождений результатов повторных измерений проявляют себя по-разному, они не зависимы друг от друга, т.е. не коррелированны. В появлении таких погрешностей не наблюдается какой-либо закономерности, поэтому предсказать значение до проведения измерений невозможно. Это и дало основание называть их случайными. Случайные погрешности не поддаются исключению из результатов измерений. Но их влияние можно уменьшить, т.е. уточнить результат измерений, с помощью увеличения числа измерений величины с последующей обработкой полученных результатов методами математической статистики (п. 3.2).Близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же средствами измерений в одинаковых условиях и с одинаковой тщательностью, называют сходимостью результатов измерений. Близость друг к другу результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами измерений, разными операторами, в разное время, но приведенных к одним и тем же условиям измерений (температуре, давлению, влажности и др.), называют воспроизводимостью результатов измерений. Иногда среди случайных погрешностей наблюдаются так называемые грубые погрешности (иначе их называют промахами). Грубая погрешность – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Причинами промахов могут являться ошибки оператора (неверный отсчет по шкале прибора, ошибки в записях или вычислениях, неправильное включение прибора); неисправность средства измерения; резкое изменение условий проведения измерений (например, внезапное изменение напряжения, вибрации, помехи). Грубые погрешности, как правило, возникают при однократных измерениях. Для уменьшения вероятности их появления проводят повторные измерения величины (два-три раза) и за результат принимают среднее арифметическое полученных отсчетов. При многократных измерениях для выявления грубых погрешностей используют специальные математические методы (п. 3.2). Результаты измерений, содержащих грубые погрешности, в расчет не берутся. Систематическая погрешность с– составляющая погрешности результата измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Выявление и оценка систематических погрешностей являются наиболее трудным моментом любого измерения и часто связаны с необходимостью проведения дополнительных исследований. Эти погрешности могут быть определены до начала измерений. По характеру проявления систематические погрешности подразделяют на постоянные и переменные. Постоянные систематические погрешности не изменяют свое значение при повторных измерениях. Они встречаются наиболее часто. Причинами этих погрешностей являются неправильная градуировка шкал средств измерений, неправильная установка начала отсчета и др. Переменные систематические погрешности при повторных измерениях могут принимать различные значения. Если переменная погрешность при повторных измерениях возрастает или убывает, то ее называют прогрессивной. Переменная погрешность при повторных измерениях также может изменяться периодически или по сложному закону. Причинами появления переменных погрешностей являются, например, износ контактирующих деталей средства измерения, действие внешних факторов, постепенное падение напряжения источника постоянного тока. Систематическая погрешность искажает (смещает) результат измерения относительно истинного (действительного) значения. Систематическая погрешность может быть более опасной, чем случайная, т.к. о ее существовании могут просто не подозревать. Поэтому с может быть причиной неправильного управления объектами, неправильного учета и брака продукции. Обнаружение с является одной из самых сложных задач метрологии. Наиболее просто выявить с можно, сопоставив результаты измерения величины, полученные с помощью изучаемого и более точного (эталонного) средства измерения (рис. 1.8).  Рис. 1.8. Схема определения систематической погрешности Значение величины Хэ, измеренное более точно, принимают за действительное, т.е. Хэ=Хд. Систематическую погрешность определяют по формуле (1.6). Результаты измерений, в которых имеется с, называются неисправленными. Правильность результатов измерений определяется близостью в них к нулю систематической погрешности. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей. С этой целью проводят: - устранение источников с до начала измерений; - устранение с в ходе измерений; - внесение поправок в результат измерений (после проведения измерений); - оценку границ неисключенных с. Наиболее рациональным является устранение источников погрешности до проведения измерения (профилактика погрешности), т.к. это упрощает и ускоряет процесс измерения. При этом оператор до начала работ должен устранить источники погрешности, например, удалением источников тепла и вибрации, экранированием (защитой) объекта измерения и измерительной аппаратуры, термостатированием, амортизацией и правильной установкой средств измерений. Погрешности конкретного средства измерения могут быть устранены путем его ремонта, регулировки. В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключающие их возникновение. Устранение с в процессе измерения проводят с применением специальных методов, к числу которых относят: - метод сравнения с мерой (замещения, противопоставления); - метод компенсации по знаку (предусматривают два наблюдения, чтобы в результат каждого измерения систематическая погрешность входила с разным знаком); - метод рандомизации (осуществление измерений величины различными методами или приборами). Подробно эти методы рассмотрены в учебном пособии А.Г. Сергеева и В.В. Крохина «Метрология». Если измерения не удается провести так, чтобы исключить какой-либо фактор, влияющий на результат, то в него вводят поправку (ее алгебраически суммируют с результатом измерения) или поправочный множитель (на него результат измерения умножают). Под поправкой q понимают систематическую погрешность, взятую с обратным знаком, т.е. q=-с. Само значение поправок и поправочных множителей находят экспериментально (указанным на рис. 1.8 способом) или в результате специальных теоретических исследований. Значение величины, полученное при измерении и уточненное путем введения в него необходимых поправок, называют исправленным результатом измерений. В реальных условиях полностью исключить систематические погрешности измерений оказывается практически невозможным, т.к. остается неучтенной погрешность вычисления поправок на влияние с, погрешность эталонных приборов (при измерении по схеме на рис. 1.8) и другие неисключенные остатки с. В этом случае определяют границы неисключенной систематической погрешности . При числе составляющих погрешности m4 границы вычисляют по формуле  , (1.8)где i - граница i-й составляющей неисключенной систематической погрешности. По форме представления погрешности измерений разделяют на абсолютные и относительные. Абсолютная погрешность измерений – это погрешность, выраженная в единицах измеряемой величины. Ее значение находят по формуле (2.1). Относительная погрешность – это отношение абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины  . (1.9)Ее обычно выражают в процентах. Например, если действительное значение массы Хд =10 г, а абсолютное значение погрешности =0,01 г, то относительная погрешность составит  .Использование относительных погрешностей значительно удобнее, т.к. по их значению можно судить о качестве полученного результата. Оценка случайной погрешностиПри проведении повторных измерений одной и той же величины мы получаем результаты измерений, некоторые из которых отличаются по числовому значению друг от друга, а некоторые совпадают. Расхождения между результатами указывают на наличие случайных погрешностей , о природе и причинах возникновения которых сказано выше. Нанесем результаты повторных измерений величины по мере их поступления на числовую ось (рис. 1.9). Маленькие кубики, показывающие число измерений, располагаются вдоль горизонтали в соответствии с измеряемыми значениями. Совокупность таких кубиков образует фигуру, называемую гистограммой. Она характеризует возможный разброс результатов измерений. 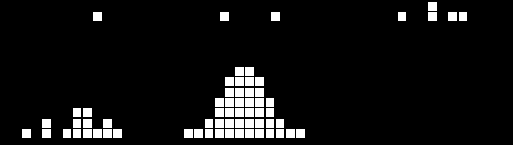 Рис. 1.9. Построение статистического распределения При увеличении числа измерений можно увидеть следующее: несмотря на то, что сами значения изменяются, их распределение подчиняется некоторому правилу. В большинстве случаев это правило следующее: основная часть измеренных значений группируется около некоторого среднего значения, причем значения, близкие к среднему будут встречаться чаще значений, отличающихся от него, и чем больше отклонение, тем реже оно встретится. Предположим, мы регистрируем все больше и больше данных. Тогда через некоторое время их распределение стабилизируется, и изменения с приходом все новых и новых измерений будут практически незаметны. Таким образом, гистограмма превращается в сглаженную кривую распределения. На рис. 1.9 показано наиболее часто встречающееся на практике распределение, называемое нормальным распределением. Таким образом, совокупность большого числа результатов повторных измерений подчиняется определенным законам. При описании этих законов метрология использует математический аппарат теории вероятности. Теория вероятности рассматривает свойства случайных явлений, которые происходят при массовых событиях, т.е. в совокупности большого числа событий, к числу которых относятся и многократно повторяемые измерения. При этом результат измерения величины, содержащий случайную погрешность, а также саму случайную погрешность , рассматривают как случайную величину.Для количественной оценки объективной возможности появления того или иного значения случайной величины служит понятие вероятности, которую выражают в долях единицы (вероятность достоверного события равна 1, а невозможного события – 0). Нормальный закон распределения случайной величины. Параметры нормального распределения Математическое описание непрерывных случайных величин (к числу которых относится и ), осуществляется обычно с помощью законов распределения случайной величины. Эти законы определяют связь между возможным значением случайной величины и соответствующей ему плотности вероятности.Наиболее распространенным при измерениях является нормальный закон распределения (рис. 1.9). Он наблюдается, когда расхождения результатов обусловлены большим числом независимых причин и ни одна из них не доминирует над остальными. На рис. 1.10, а показана кривая нормального распределения для некоторой измеряемой величины Х. По оси абсцисс отложены значения величины Х, а по оси ординат – вероятность их появления р(Х). Кривая нормального распределения симметрична линии, проходящей через центр распределения M[Х] (математическое ожидание), и имеет колоколообразную форму. Рассеяние результатов отдельных измерений относительно центра распределения характеризуется средним квадратическим отклонением . Математическое ожидание M[Х] является тем значением величины, вокруг которого группируются результаты отдельных измерений. является мерой рассеяния результатов относительно M[Х], т.е. характеризует форму кривой распределения.
Рис. 1.10. Кривые нормального распределения: а – случайной величины Х, б – случайной погрешности Перенеся начало координат в точку M[Х], получим кривую распределения случайной погрешности (рис. 1.10, б). На рис. 1.11 приведены кривые нормального распределения при различных значениях (рассеяния результатов). Сравнивая их между собой, можно установить, что рассеяние для кривой 2 меньше, чем для кривой 3, но больше, чем для кривой 1. Очевидно, что наиболее высокая сходимость наблюдается для результатов измерений, распределенных в соответствии с кривой 1. 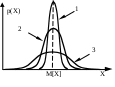 Рис. 1.11. Кривые нормального распределения с разным рассеянием значения величины, 1 2 3 Математическое выражение для описания кривой нормального распределения случайной величины (рис. 1.10, а), предложенное Гауссом, имеет вид 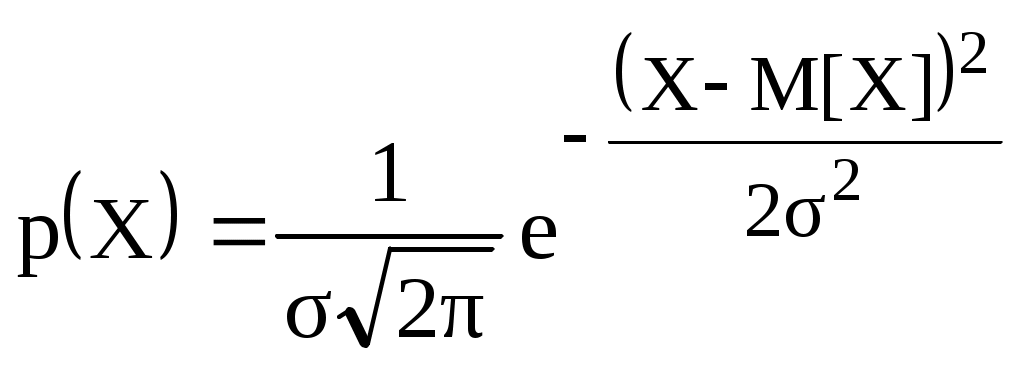 (1.10)Для описания кривой нормального распределения случайной погрешности (рис. 1.10, б) это выражение можно переписать в виде 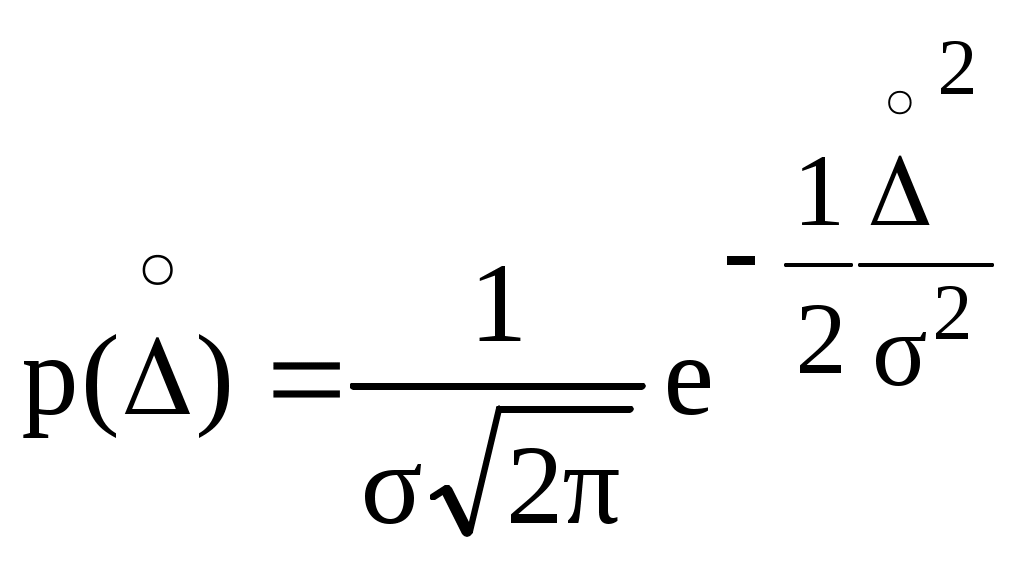 (1.11)M[Х] и являются двумя важнейшими параметрами нормального распределения случайной величины. Достаточно знать эти параметры, чтобы задать нормальное распределение. Правило трех сигм Характерное свойство нормального распределения состоит в том, что в интервале [M[Х] 1] находится около 68 % из всех его результатов измерений. В интервале [M[Х] 2] - 95 %. В интервале [M[Х] 3] - 99,73 % (рис. 1.12). Следовательно, почти все результаты измерений лежат в интервале 6 (по три в каждую сторону от M[Х]). За пределами этого интервала могут находится 0,27 % данных от их общего числа (приблизительно три из тысячи результатов измерений). 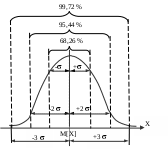 Рис. 1.12. Иллюстрация правила трех сигм Отсюда следует, что если какое-либо значение величины выходит за пределы 3, то с большой вероятностью его можно считать ошибочным. На основании этого сформулировано правило трех сигм: если при многократных измерениях (n 25…30) одной и той же величины постоянного размера сомнительный результат Хсомн отдельного измерения (максимальный или минимальный) отличается от среднего значения более чем на 3, то с вероятностью 99,7 % он ошибочен, т.е. если  3, (1.12)то Хсомн является промахом; его отбрасывают и не учитывают при дальнейшей обработке результатов измерений. Закон нормального распределения работает при числе результатов измерений n = . В реальности получают конечное число измерений, которые подчиняются закону распределения Стьюдента. При n25 распределение Стьюдента стремится к нормальному. Точечная и интервальная оценки истинного значения измеряемой величины При измерении, как уже говорилось ранее, невозможно определить истинное значение измеряемой величины. Можно лишь с большей или меньшей уверенностью оценить это значение, рассматривая его условно как параметр нормального распределения. Оценка истинного значения осуществляется по числу результатов n повторных измерений величины. Чем больше n, тем точнее можно оценить истинное значение. Выделяют понятия точечной и интервальной оценок. Точечная оценка (т.е. оценка в виде числа) истинного значения величины включает в себя оценки M[Х] и . Оценкой M[Х] является среднее арифметическое значение  , его вычисляют по формуле  , (1.13)где Хi – результат i-го единичного измерения. Оценкой является среднее квадратическое отклонение s, его вычисляют по формуле 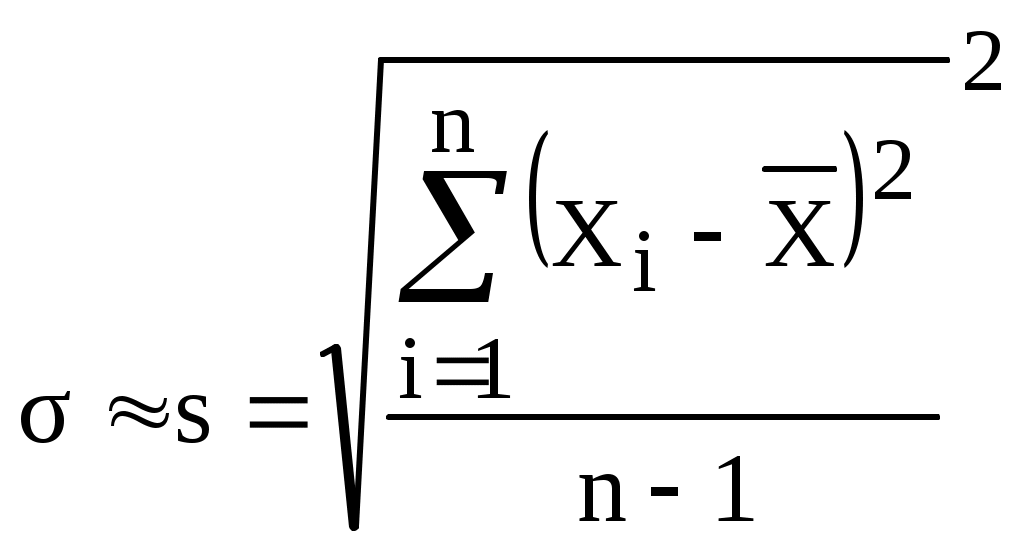 . (1.14)Оценки, приведенные в формулах (1.13) и (1.14), являются случайными величинами. Если провести повторное измерение и по его результатам вычислить 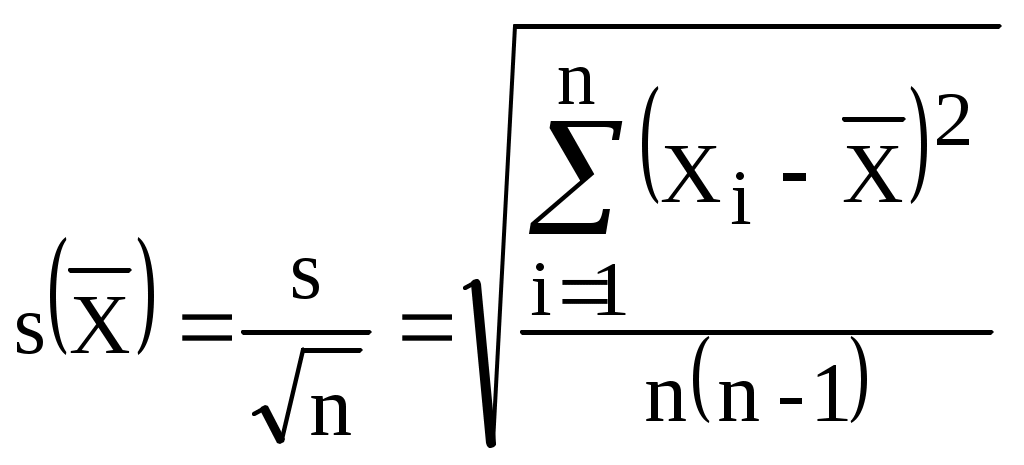 и s, то их значения будут отличаться от прежних. Повторяя измерения и вычисляя по их результатам и s, можно получить ряд значений  и s, которые также являются случайными величинами и подчиняются нормальному закону распределения. Для оценки рассеяния этих распределений используют понятие среднего квадратического отклонения среднего арифметического  , являющееся оценкой среднего квадратического отклонения результата измерения. Его определяют по формуле . (1.15)Точечные оценки используют в основном в научных исследованиях и разработках, когда проводят большое число измерений. Чем меньше число полученных результатов измерений, тем легче допустить ошибку при оценке параметров распределения. В таком случае важно определить не только M[X] и , но и получить уверенность, что истинное значение находится в некотором доверительном интервале. Для этого проводят интервальную оценку. Интервальная оценка истинного значения – это доверительный интервал, в котором с заданной доверительной вероятностью Р находится истинное значение измеряемой величины. Чаще выбирают Р = 0,9, 0,95 и 0,99. Границы доверительного интервала (рис. 1.13) определяют по формуле - Хист + , (1.16)где – это доверительная погрешность (доверительная граница случайной погрешности результата измерений).  Рис. 1.13. Доверительный интервал Достоверность измерений (один из показателей качества результатов) зависит от степени доверия к результату и характеризуется вероятностью того, что истинное значение лежит в указанных доверительных границах. определяет наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной доверительной вероятностью находится истинное значение Хист результата измерений. Причем Хист может быть в любом месте доверительного интервала (не обязательно в его середине), а с вероятностью 1-Р даже вне его. При большом числе результатов измерений (n25…30) доверительную границу случайной погрешности вычисляют по формуле  , (1.17)где zр – квантиль нормального распределения (квантильный множитель), - среднее квадратическое отклонение. Значение квантильного множителя zр определяют по таблице функции Лапласа при заданной доверительной вероятности Р (табл. 1.4) Таблица 1.4 Значения квантили нормального распределения zр
Формулу (1.17) используют для определения границ доверительного интервала, если имеется достаточно большое число результатов измерений (более 25) или если на основе предварительных опытов с достаточным числом измерений определено значение для данного метода. Чем меньше n, тем менее надежным является определение доверительного интервала приведенным выше способом. При небольшом числе результатов измерений (n25…30) используют распределение Стьюдента, и доверительную границу случайной погрешности следует рассчитывать по формуле  (1.18)где tp - коэффициент Стьюдента, s – оценка среднего квадратического отклонения Значение коэффициента Стьюдента tp определяют при заданной доверительной вероятности Р и числе результатов измерений n по табл. 1.5. Таблица 1.5. Значения коэффициента Стьюдента tP
При увеличении числа измерений (n30) распределение Стьюдента переходит в нормальное, а zp tp. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
