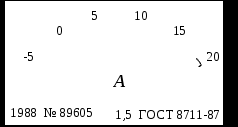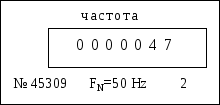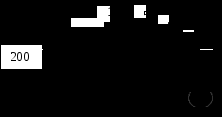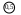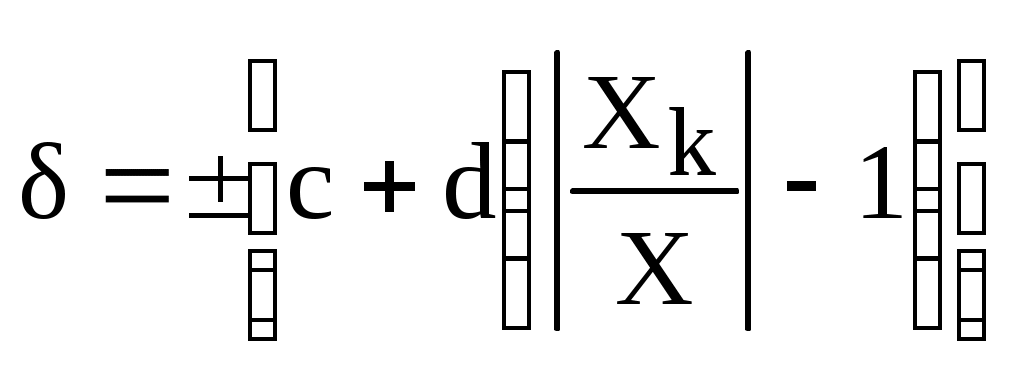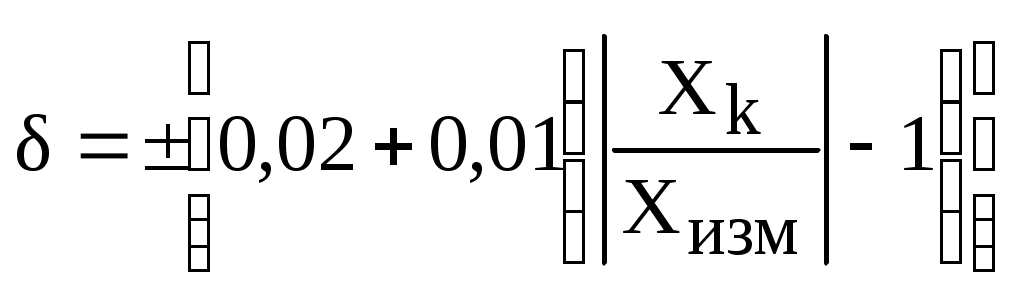Метрология. Учебное пособие. 2006 г. Введение 2 Глава измерение физических величин 4 Объекты измерений 4
 Скачать 1.42 Mb.
|
2.3. Метрологические характеристики средств измеренийКак указывалось ранее, самой важной задачей метрологии является обеспечение единства измерений, где бы, когда, кем и в каких условиях их не проводили. Если единство измерений нарушается, то, прежде всего, нарушается налаженное взаимодействие всех отраслей экономики, падает качество выпускаемой продукции, а эксплуатация сложных технических систем становится неэффективной и даже опасной. Одним из важнейших условий для реализации единства измерений является обеспечение единообразия средств измерений. Под ним понимают состояние средств измерений, когда они проградуированы в узаконенных единицах и их метрологические характеристики соответствуют нормам. Метрологическими характеристиками (МХ)называют характеристики средств измерений, оказывающие влияние на результат измерения и его погрешность. Для каждого типа средств измерений нормируют различные наборы этих характеристик. Нормирование – это установление границ на допустимые отклонения реальных МХ средств измерений от их номинальных (нормативных) значений. Нормируемые МХ устанавливают в нормативных документах на средства измерений. Посредством нормирования метрологических характеристик средств измерений обеспечивают их взаимозаменяемость и единство измерений. Реальные (действительные) значения МХ отдельного средства измерения данного типа могут быть любыми в пределах установленных границ значений номинальных метрологических характеристик. Действительные МХ определяют экспериментально. Реальные значения МХ средств измерений определяют при их изготовлении, а затем периодически проверяют в процессе эксплуатации. Если при этом хотя бы одна из МХ выходит за установленные границы, то средство измерений регулируют, подвергают ремонту или изымают из обращения. Важнейшей МХ средства измерений является его погрешность. Рассмотрим погрешность средств измерений и источники их возникновения подробнее. Далее будет представлена полная номенклатура МХ средств измерений. Погрешности средств измеренийПогрешность средств измерений (инструментальная) является одной из составляющих погрешности измерений и имеет определяющее значение для наиболее распространенных технических измерений. На рис. 2.6 приведена классификация погрешностей средств измерений по ряду признаков, которые далее рассмотрены подробнее.  Рис. 2.6. Классификация погрешностей средств измерений По закономерности проявления при повторных измерениях одной и той же физической величины принято выделять систематическую с и случайную  погрешности (или составляющие погрешности) средств измерений. В эти понятия в основном вкладывается тот же смысл, что и в понятия систематической и случайной погрешностей измерений (п. 1.3). Особенность здесь состоит в том, что всякое средство измерения предназначено для внесения определенности в исследуемый процесс, а наличие случайной составляющей погрешности приводит к неоднозначности. В связи этим первая задача, которую обычно решают при создании средств измерений, состоит в том, чтобы случайную погрешность сделать незначительной. Если это условие выполняется, а элементы, входящие в состав средства измерения, стабильны, можно путем градуировки обеспечить достаточно малые систематические погрешности средства измерения.В зависимости от условий применения измерительных устройств различают основную и дополнительную погрешности. Основной погрешностьюо средства измеренийназывают погрешность при использовании его в нормальных условиях. Нормальными являются условия, которые характеризуются значениями влияющих величин, при которых изменением результата измерений пренебрегают вследствие малости. Нормальные условия измерений устанавливают в нормативных документах на средства измерений конкретного типа. В большинстве случаев к нормальным относят следующие внешние условия: температура окружающей среды 293 К 5 К; относительная влажность воздуха 65 % 15 %; атмосферное давление 103,3 кПа 4 кПа (750 мм рт. ст. 30 мм рт. ст.); напряжение питающей электрической сети 220 В 2 % с частотой 50 Гц. Не все эти признаки нормальных условий обязательны для средств измерений. Только нормальная температура окружающей среды (с некоторым допустимым отклонением) является почти всегда обязательной. При использовании средств измерений в нормальных условиях считают, что влияющие на них величины практически никак не изменяют их характеристики. При выходе условий измерения за границы нормальных условий возникают дополнительные погрешности. Дополнительная погрешность д средства измерения – это погрешность, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального значения или вследствие ее выхода за пределы нормальной области значений. Зачастую поэтому для средств измерений устанавливают рабочие условия измерений. Рабочими называют условия измерений, при которых значения влияющих величин находятся в пределах рабочих областей, и в этих пределах нормируют дополнительную погрешность д. Рабочие условия обычно таковы, что изменения значений влияющих величин для них существенно больше, чем для нормальных условий, т.е. область рабочих условий включает в себя область нормальных условий. Например, рабочие температуры многих типов средств измерений имеют пределы -10 С…+40 С. Изменение погрешности, как и других характеристик средств измерений под действием влияющих величин, описывают функциями влияния. Функция влияния – это зависимость изменения какой-либо метрологической характеристики средства измерения от изменений влияющей величины или совокупности влияющих величин в рабочих условиях его применения. В зависимости от характера изменения величины в процессе измерения погрешности средств измерений разделяют на статические и динамические. Статической stназывают погрешность средства измерений в случае измерения величины, принимаемой за неизменную. Динамическая погрешность dyn возникает при измерении изменяющейся (в процессе измерений) величины. По форме представления погрешности делят на абсолютные, относительные и приведенные. Понятия абсолютной и относительной погрешностей средств измерений близки рассмотренным ранее погрешностям измерений (п. 1.3, формулы 1.6 и 1.9). Приведенная погрешность средства измерения представляет собой отношение абсолютной погрешности средства измерения к нормирующему значению ХN. Нормирующее значение – это условно принятое значение величины, постоянное во всем диапазоне измерений или в части диапазона. Приведенная погрешность вычисляется по формуле  . (2.15)Часто за ХN принимают верхний предел измерений или диапазон измерений средства измерений. Выражают приведенную погрешность обычно в процентах. Чрезвычайно важным для применения средств измерений и правильной оценки погрешности измерений, получаемой при их использовании, являются сведения о зависимости погрешности от значения измеряемой величины в пределах диапазона измерений, а также сведения об изменениях этой погрешности под действием влияющих величин. Зависимость погрешности от значения измеряемой величины определяется принятой конструкцией (схемой) и технологией изготовления средства измерения. Из-за несовершенства конструкции и технологии изготовления реальная функция преобразования Y=fp(X) средства измерения отличается от номинальной Y=fн(X). Отклонения реальной функции преобразованияот номинальной зависят от значения измеряемой величины. По этому признаку погрешности принято разделять на аддитивную, мультипликативную, линейности и гистерезиса (рис. 2.7).
Рис. 2.7. Реальная и номинальная функции преобразования: а, б – аддитивная погрешность, в, г – мультипликативная погрешность, д – погрешность линейности, е – погрешность гистерезиса Аддитивная (получаемая путем сложения) – это погрешность, которая остается постоянной при всех значениях измеряемой величины. Аддитивные погрешности выражают внутренние свойства средства измерений, присущие ему независимо от внешних воздействий. Примерами такого рода служит погрешность, вызванная сдвигом шкалы прибора и погрешность, обусловленная ненулевым порогом реагирования («погрешность нуля»). На рис. 2.7, а показано смещение реальной функции преобразования Y = fp(X) относительно номинальной Y = fн(X), при этом выходной сигнал средства измерения при всех значениях измеряемой величины Х будет больше или меньше на одну и ту же величину, чем он должен быть, в соответствии с номинальной функцией преобразования. Если аддитивная погрешность является систематической, то она может быть устранена. Для этого в средствах измерений обычно имеется специальный настроечный узел (корректор) нулевого значения выходного сигнала. Если аддитивная погрешность является случайной, то ее нельзя исключить полностью, а реальная функция преобразования смещается по отношению к номинальной во времени произвольным образом. При этом для реальной функции преобразования можно определить некоторую полосу (рис. 2.7, б),ширина которой остается постоянной при всех значениях измеряемой величины. Возникновение случайной аддитивной погрешности обычно вызвано трением в опорах, контактными сопротивлениями, дрейфом нуля, шумом и фоном средства измерения. Мультипликативная (получаемая путем умножения) – это погрешность, которая линейно возрастает (или убывает) с увеличением измеряемой величины. Примером такой погрешности является погрешность измерительного преобразователя, обусловленная отличием действительного коэффициента преобразования от номинального. Графически появление мультипликативной погрешности интерпретируется поворотом реальной функции преобразования относительно номинальной (рис. 2.7, в). Если мультипликативная погрешность является случайной, то реальная функция преобразования представляется полосой, показанной на рис. 2.7, г. Причиной возникновения мультипликативной погрешности обычно является изменение коэффициентов преобразования отдельных элементов и узлов средств измерений. На рис. 2.7, д показано взаимное расположение номинальной и реальной функций преобразования средства измерения в случае, когда отличие этих функций вызвано нелинейными эффектами. Если номинальная функция линейная, то вызванную таким расположением реальной функции преобразования систематическую погрешность называют погрешностью линейности. Ее причинами могут быть конструкция средства измерения и нелинейные искажения функции преобразования, связанные с несовершенством технологии производства. Наиболее существенной и трудно устраняемой систематической погрешностью измерительных устройств является погрешность гистерезиса, выражающаяся в несовпадении реальной функции преобразования при увеличении (прямой ход) и уменьшении (обратный ход) измеряемой величины (рис. 2.7, е). Погрешность гистерезиса приводит к вариации выходного сигнала. Вариация представляет собой разность показаний, получаемых при измерениях одного и того же значения измеряемой величины, сначала – приближением к нему со стороны меньших значений (прямой ход), затем – со стороны больших значений шкалы (обратный ход). Причинами гистерезиса являются люфт и сухое трение в механических передающих элементах, гистерезисный эффект в ферромагнитных материалах, внутреннее трение в материалах пружин, явление упругого последействия в упругих чувствительных элементах, явление поляризации в электрических, пьезоэлектрических и электрохимических элементах и др. Метрологические характеристики средств измерений и их нормированиеНормирование МХ производят согласно положениям ГОСТ 8.009 «ГСИ. Нормируемые метрологические характеристики средств измерений». Данный стандарт устанавливает номенклатуру МХ, правила их выбора и способы нормирования. Номенклатура нормируемых МХ и полнота, с которой они должны описывать свойства средств измерений, зависит от их назначения, условий эксплуатации, режима работы и других факторов. Выбор нормируемых МХ зависит от вида средства измерений и осуществляется в процессе разработки, освоения производства и аттестации средства измерений. У средств измерений, используемых преимущественно для высокоточных измерений, нормируется достаточно большое количество МХ. Принципы выбора и нормирования МХ Важно, чтобы номенклатура МХ и способы их выражения были оптимальными. Целесообразно нормировать комплекс МХ таким образом, чтобы он не был очень большим, а каждая нормируемая характеристика в нем отражала бы конкретные свойства средства измерения и при необходимости могла быть проконтролирована. Нормируемые МХ должны быть выражены в такой форме, чтобы с их помощью можно было обосновано решать практически любые измерительные задачи и одновременно достаточно просто проводить контроль средств измерений на соответствие этим характеристикам. 3. Нормируемые МХ должны обеспечивать возможность статистического объединения, суммирования составляющих инструментальной погрешности измерений instr. В общем случае инструментальную погрешность можно представить в виде  , (2.16)где  - символ статистического объединения составляющих5; о, д, dyn, int, – составляющие инструментальной погрешности: соответственно основная, дополнительная, динамическая и погрешность взаимодействия, L - число дополнительных погрешностей, равное сумме всех величин, существенно влияющих на погрешность в реальных условиях.Погрешность взаимодействия  обусловлена взаимодействием средства измерения с объектом измерений или другими средствами измерений, включенными последовательно с ним в измерительную систему. Средства измерений обладают свойствами отбирать или отдавать энергию через свои входные или выходные цепи (такие свойства называют импедансами). Это приводит к изменению значения измеряемой величины и, следовательно, к появлению составляющей погрешности взаимодействия  . Нормируемые МХ должны быть инвариантны к условиям применения и режиму работы средства измерения, отражать только его свойства. Выбор МХ необходимо осуществлять так, чтобы пользователь имел возможность рассчитывать по ним характеристики средства измерений в реальных условиях эксплуатации. Нормируемые МХ, приводимые в нормативных документах, отражают свойства не только отдельно взятого экземпляра средства измерения, а всей совокупности средств измерений данного типа, т.е. являются номинальными. МХ отдельного средства измерения данного типа могут быть любыми в пределах области значений номинальных МХ. Общий подход при нормировании метрологических характеристик состоит в том, что для них устанавливаются номинальные функции и номинальные значения (например, номинальная функция преобразования, номинальная функция влияния, номинальное значение информативного параметра на выходе, номинальное значение постоянной времени). Для остальных характеристик устанавливаются пределы допустимых значений (например, пределы допускаемой основной погрешности, пределы допускаемой вариации). Номенклатура метрологических характеристик и способы их нормирования представлены в табл. 2.1. В зависимости от назначения и свойств средств измерений для них нормируют не все вышеперечисленные МХ, а только некоторые из них. Для средств измерений, используемых по отдельности, не нормируют функцию преобразования, импедансы и неинформативные параметры выходного сигнала, поскольку эти характеристики не существенны для них. Для средств измерений, входящих в сложные измерительные установки (системы), эти характеристики описывают эффекты их взаимодействия, поэтому должны нормироваться стандартами. Можно не нормировать случайную составляющую погрешности, если она существенно меньше систематической. Таблица 3.1 Номенклатура метрологических характеристик (МХ) и способы их нормирования
* Например, для вольтметра переменного электрического тока напряжение является информативным, а частота тока – неинформативным параметром. Классы точности средств измеренийУчет всех нормируемых МХ средств измерений – сложный и трудоемкий процесс, проводимый, как правило, только при измерениях высокой точности (лабораторных, метрологических). При технических измерениях, широко используемых на практике, такой учет обычно не проводят. Для таких средств измерений принято устанавливать классы точности. Класс точности – это обобщенная характеристика средств измерений данного типа, как правило отражающая их точность, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность измерений. Для установления класса точности средств измерений применяют общие правила, в соответствии с которыми проводят количественную оценку гарантированных границ погрешности средств измерений данного типа. Класс точности не устанавливают для средств измерений, у которых отдельно нормируют систематическую и случайную составляющие основной погрешности и для которых существенны динамические погрешности. Необходимо помнить, что класс точности не является непосредственной характеристикой точности измерений, выполняемых с помощью этих средств измерений, поскольку точность измерений зависит и от метода измерения, взаимодействия с объектом, условий измерения и т.д. Например, чтобы измерить величину с точностью 1 %, недостаточно выбрать средство измерения с погрешностью 1 %. Необходимо, чтобы выбранное средство измерения должно обладать гораздо меньшей погрешностью, т.к. нужно учесть как минимум еще погрешность метода. Впервые термин «класс точности» был введен в 30-е г. ХХ в. применительно к стрелочным приборам для определения основной погрешности средств измерений (в нормальных условиях) и классификации последних по точности. Эта характеристика позволила четко стандартизировать измерительные приборы, облегчить выбор средств измерений, проводить ориентировочную оценку точности измерений. Требования к назначению, применению и обозначению классов точности регламентированы ГОСТ 8.401. Класс точности конкретного типа устанавливают в технической документации, сопровождающей данное средство измерения с обязательной ссылкой на стандарт или технические условия. Если средство измерения предназначено для измерений нескольких величин или для одной, но в разных диапазонах, то могут быть присвоены разные классы точности как по измеряемым величинам, так и по диапазонам. Классы точности присваивают при разработке средств измерений по результатам приемочных испытаний. В связи с тем, что в процессе эксплуатации средств измерений их метрологические характеристики обычно ухудшаются, то допускается понижать класс точности по результатам поверки или калибровки средства измерения. Класс точности средства измерения выражают пределами допускаемой погрешности, выраженной в абсолютной, относительной или приведенной форме. Способ выражения погрешностей зависит от характера их изменения по диапазону измерения, назначения и условия применения средства измерения. Если погрешность результатов измерений в данной области измерений принято выражать в единицах измерения величины или делениях шкалы, то принимают форму абсолютных погрешностей (например, для мер массы, длины). Если границы абсолютных погрешностей в пределах диапазона измерений практически постоянны, то используют форму приведенной погрешности, а если их нельзя считать постоянными, то применяют форму относительной погрешности. Таким образом, ГОСТом установлены три основных формы представления пределов допускаемой погрешности средств измерений. Они рассмотрены ниже. Определяя класс точности, нормируют (устанавливают) прежде всего пределы допускаемой основной погрешности. В ряде случаев вместе с основной нормируют пределы допускаемой дополнительной погрешности, форма представления которой может отличаться от формы представления основной погрешности. Формы представления погрешностей при установлении классов точности 1 способ. Пределы допускаемой основной абсолютной погрешности устанавливают в виде одночленной формулы = а, (2.17) либо в виде двухчленной формулы = (а + bХ), (2.18) где Х – значение измеряемой величины, а и b – положительные числа, не зависящие от Х. и Х выражаются в единицах измеряемой величины либо в делениях шкалы прибора. Абсолютная погрешность выражается одним числом (формула 2.17), если она имеет аддитивный характер (рис. 2.8, а) и двучленом (формула 2.18), если она имеет аддитивно- мультипликативный характер (рис. 2.8, б).
Рис. 2.8. Характер изменения границ абсолютных погрешностей средств измерений: а – аддитивный, б – аддитивно-мультипликативный, в – мультипликативный 2 способ. Пределы допускаемой основной приведенной погрешности устанавливают по формуле:  , (2.19)где - пределы допускаемой абсолютной погрешности, устанавливаемой по формуле 2.17, ХN – нормирующее значение, выраженное в тех единицах, что и , р – отвлеченное положительное число, выбираемое из ряда: 110n; 1,510n; 210n; 2,510n; 410n; 510n; 610n, где n = 1, 0, -1, -2 и т.д. В этом случае абсолютная погрешность имеет аддитивный характер (рис. 2.8, а). Нормирующее значение ХN устанавливают равным верхнему пределу измерений для средств измерений с равномерной или степенной шкалой с нулевым значением на краю или вне диапазона измерений. Для электроизмерительных приборов с нулевой отметкой внутри диапазона измерений ХN допускается устанавливать равным сумме модулей пределов измерений. Для средств измерений, для которых принята шкала с условным нулем, ХN равно модулю разности пределов измерений. Для средств измерений с установленным номинальным значением ХN равно номинальному значению. 3 способ. Пределы допускаемой основной относительной погрешности устанавливают по одночленной формуле  , (2.20)где = bХ (b=tg на рис. 2.8, в), q – отвлеченное положительное число, выбираемое из ряда, приведенного выше, либо двухчленной формулой 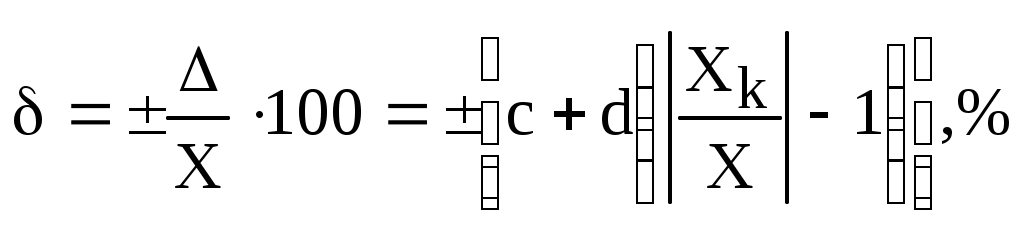 , (2.21)где = (а + bХ), Хk – больший по модулю из пределов измерения средства измерения, с и d – отвлеченные положительные числа, выбираемые из ряда, приведенного выше. Формула (2.20) применяется, если погрешность средства измерения имеет в основном мультипликативный характер (рис. 2.8, в), а формулу (2.21) – при аддидивно-мультипликативном характере (рис. 2.8, б). Обозначение классов точности Обычно класс точности указывается в виде арабских или римских цифр, а также букв латинского алфавита. Обозначения классов точности наносят на циферблаты, щитки и корпуса средств измерений (рис. 2.9), приводят в нормативных и технических документах.
Рис. 2.9. Внешний вид шкал средств измерений: а – вольтметр, б – амперметр, в – частотомер, г – мегаомметр Согласно ГОСТ 8.401 обозначение классов точности вводится в зависимости от способов задания пределов допускаемых погрешностей. Возможны четыре варианта обозначения класса точности. 1) Если пределы допускаемой основной погрешности выражены в абсолютной форме (формулы 2.17, 2.18), то класс точности средства измерения обозначают заглавными буквами латинского алфавита (например: А, В, С) или римскими цифрами (I, II, III и т. д.). Соответствие букв значению абсолютной погрешности раскрывается в технической документации на данное средство измерения. Обычно чем дальше буква от начала алфавита, тем больше значение допускаемой абсолютной погрешности (например, прибор класса В более точен, чем класса С). 2) Если пределы допускаемой основной погрешности выражены в приведенной форме (формула 2.19), то класс точности средств измерений обозначается арабской цифрой (возможны дополнительные условные знаки), указывающей предел допускаемой погрешности. Например, класс точности прибора 1,5 означает, что = 1,5 %. 3  ) Если пределы допускаемой основной погрешности выражены в относительной форме (формула 2.20), то класс точности средств измерений обозначается арабской цифрой в окружности, указывающей предел допускаемой погрешности. Например, класс точности прибора 0,5 означает, что = 0,5 %.4) Если пределы допускаемой основной погрешности выражены в относительной форме (формула 2.21), то класс точности средств измерений обозначается двумя цифрами, соответствующими значениям c и d. Например, класс точности прибора 0,02/0,01 означает, что с = 0,02, d = 0,01. В таблице 2.2 приведены примеры обозначения классов точности в документации и на средствах измерения. Таблица 2.2 Классы точности средств измерений
Пределы допускаемых дополнительных погрешностей непосредственно не учитывают при установлении класса точности средства измерения. В технической документации их устанавливают обычно в виде дольного (кратного) значения предела допускаемой основной погрешности. Пределы всех основных и дополнительных допускаемых погрешностей выражаются не более чем двумя значащими цифрами. Ниже приведены примеры определения пределов допускаемой погрешности средств измерения с использованием классов точности. Пример 1. Термоэлектрический преобразователь ТХА-9310 выпускают трех классов точности: А, В и С. Пределы допускаемых погрешностей составляют: А = 0,004t, В = 0,0075t, С = 0,015t (t – текущая температура). Необходимо определить значения пределов допускаемых абсолютных погрешностей для преобразователей этих классов точности при результате измерения температуры t = 200 С. Решение. А = (0,004 200) = 0,8 С, аналогично В = 1,5 С, С = 3 С. Пример 2. На рис. 2.9 представлены шкалы средств измерений с указанием значений измеряемых величин и классов точности. Необходимо определить пределы допускаемых абсолютных погрешностей указанных приборов. Решение. Класс точности вольтметра, равный 0,5 (рис. 2.9, а) означает, что нормированы пределы допускаемой приведенной погрешности прибора, т.е. = 0,5 %. Следовательно, необходимо воспользоваться формулой 2.19 для определения пределов допускаемой абсолютной погрешности. Нормирующее значение равно верхнему пределу измерений (ХN =100 В), т.к. нулевое значение равномерной шкалы находится на краю диапазона измерений. Отсюда:  Следовательно, предел допускаемой погрешности вольтметра не превышает 0,5 В, а измеряемое напряжение U при показании 65 В составляет (65,0 0,5) В. Класс точности амперметра, равный 1,5 (рис. 2.9, б), означает также нормирование пределов допускаемой приведенной погрешности прибора, т.е. = 1,5 %. Нормирующее значение равно сумме модулей пределов измерений (ХN =25 А), т.к. нулевая отметка находится внутри диапазона измерений. Поэтому в соответствии с формулой 2.19 допускаемая погрешность равна  Таким образом, предел допускаемой погрешности амперметра составляет ±0,38 А. На рис. 2.9, в рядом с цифровым табло частотомера указан класс точности 2. Это указывает на нормирование пределов допускаемой приведенной погрешности прибора ( = 2 %). Нормирующее значение равно номинальному значению (ХN =50 Гц), поэтому  и измеряемая частота равна (47 1) Гц.  Класс точности мегаомметра с неравномерной шкалой, равный 2,5 (рис. 2.9, г), свидетельствует о том, что допускаемая относительная погрешность прибора не превышает 2,5 %. Следовательно, необходимо воспользоваться формулой 2.20 для определения абсолютной погрешности.  R= (40 1) МОм. Пример 3. Амперметр с диапазоном измерения -50…50 А имеет класс точности, равный 0,02/0,01. Необходимо определить, чему равна сила тока в цепи при показании 25,625 А. Решение. Класс точности прибора указывает на нормирование пределов допускаемой относительной погрешности прибора. Вначале определим значение этих пределов по формуле 3.21 (с=0,02, d=0,01, Хk=50 А).  Затем вычислим пределы допускаемой абсолютной погрешности, используя формулу 2.20  Следовательно, сила тока в цепи с учетом правил округления равна (25,625 0,008) А. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и 
(вариация выходного сигнала)
;
