Метрология. Учебное пособие. 2006 г. Введение 2 Глава измерение физических величин 4 Объекты измерений 4
 Скачать 1.42 Mb.
|
3.2. Обработка результатов измеренийЗадача обработки результатов измерений заключается в определении погрешности измерения величины. При многократных измерениях обычно дают точечную оценку результата измерений или указывают доверительный интервал. Исходной информацией для обработки является ряд из n результатов измерений, из которых исключены известные систематических погрешности: Х1, Х2, Х3 ….. Хn. Число измерений n зависит как от требований к точности получаемого результата, так и от реальной возможности выполнить повторные измерения. Ниже рассмотрены алгоритмы обработки результатов однократных и многократных измерений6. Однократные измерения находят широкое применение во многих областях производственной деятельности, в быту, торговле. Как правило, их проводят, если при измерении происходит разрушение объекта измерений, отсутствует возможность повторных измерений или имеет место экономическая целесообразность. В обычных условиях нас устраивает их точность и простота выполнения. При повышенных требованиях к точности измерений для уменьшения погрешности результата измерений проводят повторные измерения одной и той же величины в одинаковых условиях, используя одни и те же средства измерений. Такие измерения характерны при выполнении метрологических работ, в лабораторных исследованиях, при входном контроле продукции и т.п. Главной особенностью многократных измерений является получение и использование большого объема измерительной информации. Обработку результатов многократных измерений рекомендуется начать с проверки на отсутствие грубых погрешностей. Если оператор в ходе измерения обнаруживает такой результат и достоверно находит его причину, он вправе отбросить его и провести (при необходимости) дополнительное измерение взамен отброшенного. При обработке уже имеющихся результатов измерений произвольно отбрасывать отдельные результаты нельзя, т.к. это может привести к фиктивному повышению точности результата. Поэтому для обнаружения промахов применяют специальные критерии (два из них рассмотрены ниже). В большинстве случаев при обработке многократных измерений исходят из предположения нормального закона распределения результатов и погрешностей измерений. Ниже рассмотрен один из способов проверки соответствия распределения результатов измерений нормальному закону (построение гистограммы). Обнаружение грубых погрешностей в результатах измеренийДля выявления грубых погрешностей (промахов) в результатах измерений задаются вероятностью того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений. Эту вероятность называют уровнем значимости, =1-Р. Обычно выбирают равным 0,1 или 0,05. В ряду результатов измерений определяют Хсомн (наибольшее или наименьшее значение) и вычисляют отношение 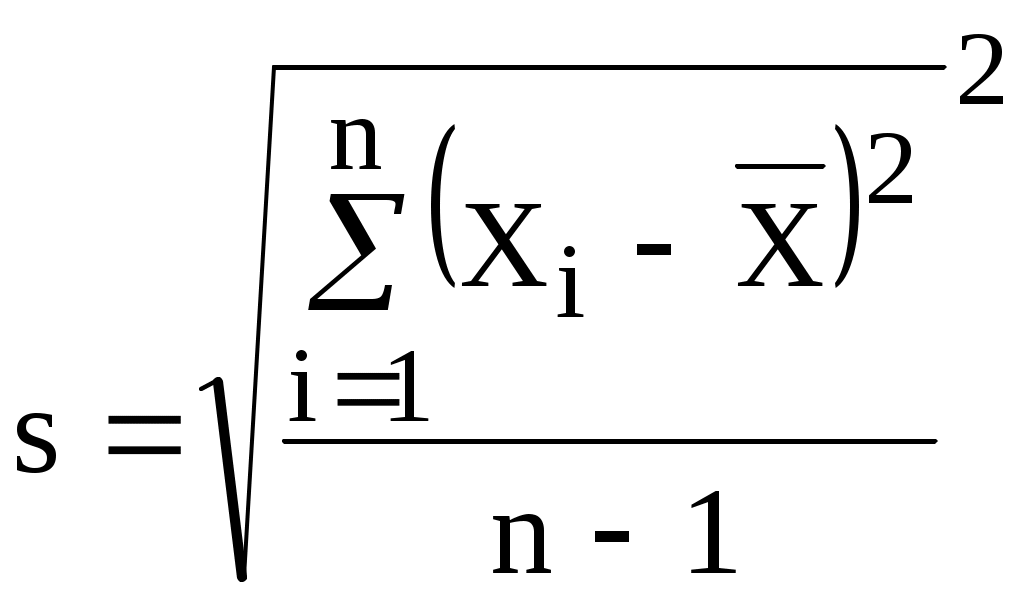 , (3.1)где  и s – среднее арифметическое значение и среднее квадратическое отклонение, рассчитываемые по формулам (3.2) (3.3)Далее сравнивают с табличным значением критерия т (табл. 3.1) при заданном значении и числе измерений n. Если окажется, что т, то в результатах отсутствует грубая погрешность, в противном случае (т), результат Хсомн содержит грубую погрешность и его из дальнейшей обработки исключают. Таблица 3.1 Значения т
Пример. Определить, содержится ли грубая погрешность в следующих результатах шестикратного взвешивания изделия (г) при уровне значимости =0,05. 72,365; 72,357; 72,352; 72,356; 72,344; 72,340. Решение. Рассчитаем и s по формулам (3.2) и (3.3): = 72,352 г, s = 0,0091 г.Хсомн =72,365. Вычислим по формуле (3.1)  По табл. 3.1 при =0,05 и n=6 найдем т=2,067. Ответ: грубых погрешностей в результатах нет. Если число измерений велико (n25), то выявление грубых погрешностей можно проводить по правилу трех сигм (см. формулу (1.12)). Обработка результатов измеренийОднократные прямые измерения При однократных прямых показание средства измерения Хизм является результатом измерения, а погрешность используемого средства определяет погрешность результата. Необходима уверенность в том, что субъективная погрешность и погрешность выбранного средства измерения мала по сравнению с допускаемой погрешностью измерения. Вопросы выбора средств измерений рассмотрены выше. При однократном измерении получают одно значение отсчета Хизм и результат записывают в виде Хизм си, где си – погрешность средства измерения. Многократные прямые измерения Общая последовательность обработки результатов измерений в соответствии с ГОСТ 8.207 состоит из следующих этапов. Этап 1. Вычисление среднего арифметического значения по формуле (3.2).Этап 2. Расчет среднего квадратического отклонения s по формуле (3.3). Этап 3. Проверка наличия грубой погрешности в результатах (см. выше). Если она обнаружена, то этот результат следует отбросить и повторить этапы 1 и 2. Этап 4. Проверка соответствия результатов измерений закону нормального распределения (см. ниже). Этап 5. Вычисление среднего квадратического отклонения 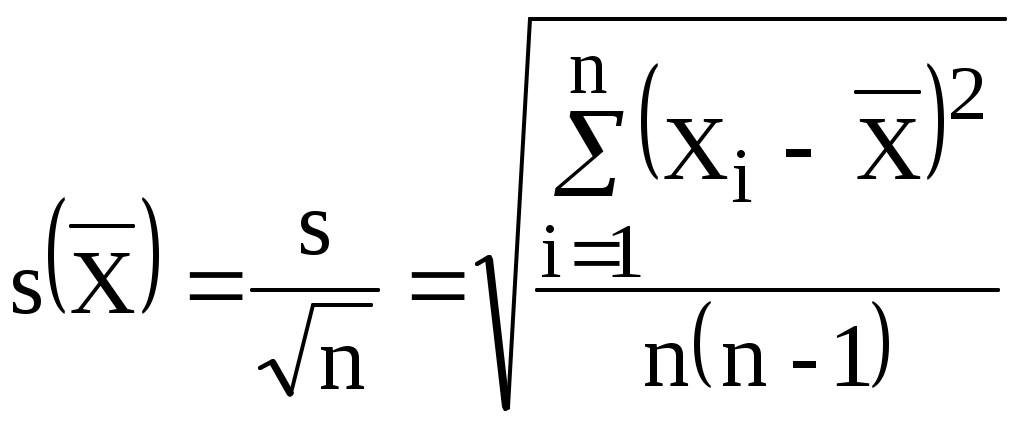 среднего арифметического по формуле  (3.4)Этап 6. Определение коэффициента Стьюдента tp при заданном значении доверительной вероятности Р и числе результатов измерений n по табл. 1.5. Этап 7. Определение доверительных границ случайной погрешности при заданном значении доверительной вероятности Р по формуле  (3.5)Этап 8. Определение границ неисключенной систематической погрешности результата измерения по формуле.  (3.6)где m - число составляющих погрешности Неисключенная систематическая погрешность образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности метода, средств измерений, субъективные погрешности. Эти составляющие погрешности находят нестатистическими методами. Этап 9. Вычисление доверительных границ погрешности результата измерений . Данная операция осуществляется путем суммирования случайной составляющей погрешности и неисключенной систематической составляющей погрешности . При этом вычисляют отношение  и в зависимости от полученного значения определяют погрешность результата измерения по правилам, изложенным в табл. 3.2.Таблица 3.2 Определение погрешности результата измерения
Этап 10. Запись результата измерений с учетом правил округления в виде  при доверительной вероятности Р и числе измерений n.Пример. Необходимо произвести обработку результатов измерений сопротивлений катушки сопротивления при заданной доверительно вероятности Р=0,95. Значения сопротивления Хi (МОм) приведены в табл. 3.3. Погрешность средства измерения равна 1 МОм. Таблица 3.3 Результаты измерений и вычислений
Решение. По формулам (3.2) и (3.3) вычислим среднее арифметическое значение и среднее квадратическое отклонение  МОм МОмПроверим, имеется ли в результатах грубая погрешность (Хсомн=398). По формуле (3.1) вычислим  При =0,05 и n=10 т=2,414. т, следовательно, грубых погрешностей в результатах нет. Вычислим  по формуле (3.4). МОмДля Р=0,95 и n=10 коэффициент Стьюдента tр = 2,26 (табл. 1.5). По формуле (3.5) находим доверительную границу случайной погрешности:  Имеется одна составляющая неисключенной погрешности (погрешность средства измерения), т.е. m=1. Следовательно, граница неисключенной систематической погрешности =1 МОм Вычислим отношение  В соответствии с правилами, указанными в табл. 3.2, погрешность результата измерения составляет 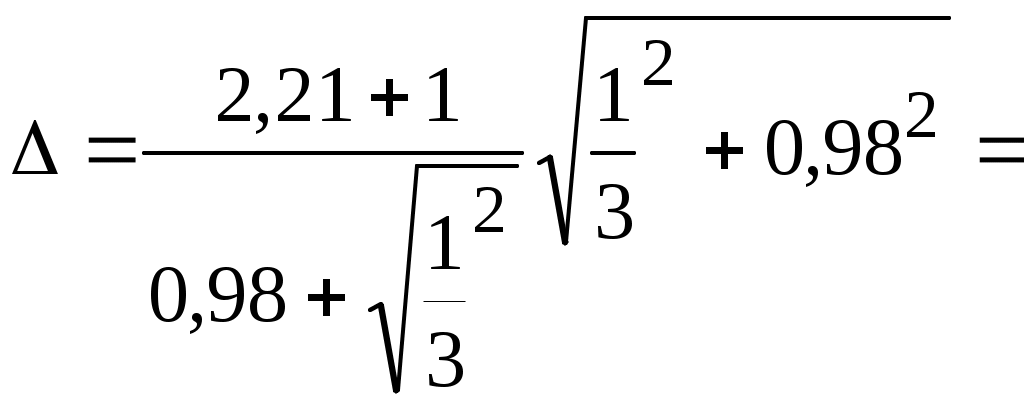 2,34Запишем результат измерений, учитывая рекомендации по округлению: (391,9 2,3) МОм при Р=0,95 и n=10. Однократные косвенные измерения При косвенных измерениях искомую величину Q не измеряют непосредственно, а вычисляют по результатам измерений других величин на основании известной функциональной зависимости Q = f (X1, X2,…Xm) (3.7) где X1, X2,…Xm – величины-аргументы, подлежащие прямым измерениям Вид функции f должен быть известен из теоретических предпосылок или установлен экспериментально. Значение величины Q определяют согласно уравнению (3.7). Абсолютные погрешности величин-аргументов 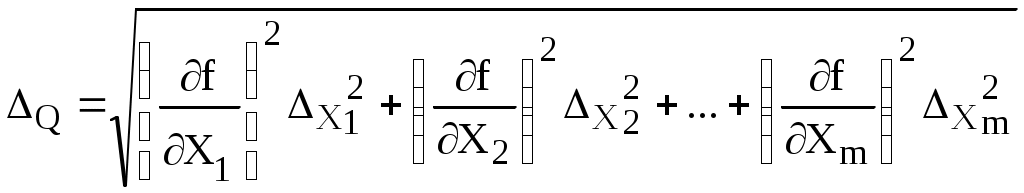 ,  , … определяют исходя из значения погрешностей средств измерений. Затем вычисляют значение погрешности Q искомой величины (3.8)где -   - частные производные по составляющим аргументамРезультат измерения записывают в виде Q Q Многократные косвенные измерения Последовательность обработки результатов многократных косвенных измерений для некоррелированных величин Х1, Х2, …Xj,…Xm (m – число величин-аргументов) состоит из ряда этапов. Этап 1. Вычисление средних арифметических значений  ,  ,… ,… для каждой из измеряемых прямым методом величин Х1, Х2, …Хj… Xm по формуле (3.2).Этап 2. Определение результата косвенного измерения  по известной функциональной зависимости .Этап 3. Расчет средних квадратических отклонений  ,  ,… для каждой из измеренных величин Х1, Х2, …Xj,…Xm по формуле (3.3).Этап 4. Расчет средних квадратических отклонений  ,  ,… по формуле (3.4).Этап 5. Вычисление среднего квадратического отклонения 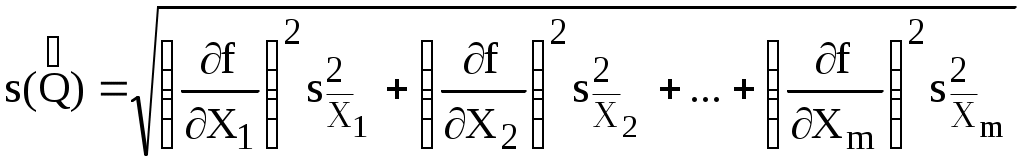 для искомой величины Q по формуле  (3.9)где  ,  ,… - частные производные по составляющим аргументам.Этап 6. Определение коэффициента Стьюдента tp по табл. 1.5 при заданном значении доверительной вероятности Р и эффективном числе степеней свободы kэф, которое используют вместо n. kэф определяют по формуле 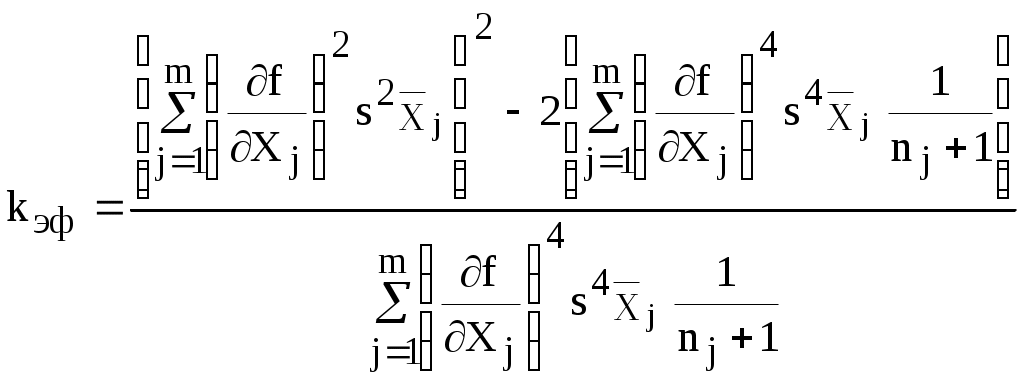 (3.10)где nj – число измерений j-ой величины-аргумента. Если все величины-аргументы измерены одинаковое число раз n, то kэф=n. Этап 7. Определение доверительных границ случайной погрешности по формуле  .Этап 8. Определение границ неисключенной систематической погрешности результата измерения по формуле (3.6). Этап 9. Вычисление доверительных границ погрешности результата измерений . При этом вычисляют отношение  и в зависимости от полученного значения определяют по правилам, изложенным в табл. 3.2.Этап 10. Запись результата измерений с учетом правил округления в виде  при доверительной вероятности Р и числе измерений n.n указывают для того аргумента, при измерении которого выполнено наименьшее число наблюдений. Рекомендуемые правила по округлению результатов измерений Поскольку погрешности измерений определяют лишь зону неопределенности результатов, их не требуется знать очень точно. В окончательной записи погрешность измерения принято выражать числом с одной или двумя значащими цифрами. Погрешность измерения указывают двумя значащими цифрами, если первая из них равна 1 или 2, и одной цифрой – если первая 3 и более. Результат измерения округляют до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Например: (5,08 0,12) м; (25,1 0,4) С; (6,046 0,008) с. Округление производят лишь в окончательном ответе, а все промежуточные вычисления проводят с одним или двумя лишними знаками. Проверка соответствия результатов измерения закону нормального распределенияПроверка соответствия результатов многократных измерений закону нормального распределения – это один из первых этапов их обработки. При числе наблюдений n40 для проверки нормальности распределения результатов строят гистограмму. Если огибающая гистограмму кривая соответствует по внешнему виду «колоколу» Гаусса, то это указывает на нормальный закон распределения результатов измерений. Построение гистограммы рассматривается ниже. Закон распределения также определяют, используя статистический критерий Пирсона (хи-квадрат) при n50. При 50n15 для проверки нормальности закона распределения применяется составной критерий (d-критерий), приведенный в ГОСТ 8.207. При n15 принадлежность экспериментального распределения к нормальному закону не проверяется Построение гистограммы Гистограмма дает наглядное графическое представление о распределении результатов измерений. Ее строят для интервальных рядов данных, причем число результатов должно быть достаточно большим (не менее 40). Гистограмма представляет собой ступенчатую фигуру, состоящую из прямоугольников, основания которых равны границам интервалов, а высота соответствует абсолютным или относительным частотам попадания результатов в интервалы. Обычно построение гистограммы состоит из нескольких этапов: 1. Расчет размаха R из n результатов измерений (размах – это разница между наибольшим Хmax и наименьшим Xmin значениями)  . (3.11)2. Определение количества интервалов k по формуле k = 1 + 3,3 lg n (3.12) или по упрощенной формуле k =  (3.13)Полученное значение k можно округлить. Обычно 6k20. 3. Вычисление ширины интервалов гистограммы h h =  . (3.14)4. Расчет границ интервалов. Границы интервалов выбирают обычно таким образом, чтобы они не совпадали с результатами измерений и крайние интервалы были заполнены. Подсчет числа попаданий результатов в интервалы. Полученные результаты сводят в таблицу. Построение столбчатой гистограммы. Если полученная гистограмма соответствует «колоколу» Гаусса (рис. 2.3), то результаты измерений распределены по нормальному закону. Пример. 50-кратные измерения напряжения (В) дали результаты, приведенные ниже. Необходимо определить закон распределения результатов измерения, построив гистограмму.
Решение. Рассчитаем размах результатов R по формуле (3.11) R = 20,80 – 20,40 = 0,40 В. Определим количество интервалов по формуле (3.12): k = 1 +3,3 lg 50 = 6,6 7. По формуле (3.14) вычислим ширину интервалов h =  ВДалее составим таблицу, в которую запишем границы интервалов и частоту попадания результатов в указанные интервалы (табл. 3.4). Наименьший результат измерения 20,40 В, поэтому нижнюю границу первого интервала целесообразно выбрать равной 20,40 -  = 20,37 ВЧтобы границы интервалов не совпадали с результатами, добавим к ним один разряд. Таблица 3.4 Расчет гистограммы
Строим гистограмму. По оси абсцисс откладываем границы интервалов, а по оси ординат – абсолютные или относительные частоты (рис. 3.1).  Рис. 3.1. Гистограмма Легко и достаточно быстро построить такую гистограмму можно в редакторе EXCEL. Полученная гистограмма соответствует «колоколу» Гаусса, что говорит о нормальном распределении результатов измерений напряжения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
; 
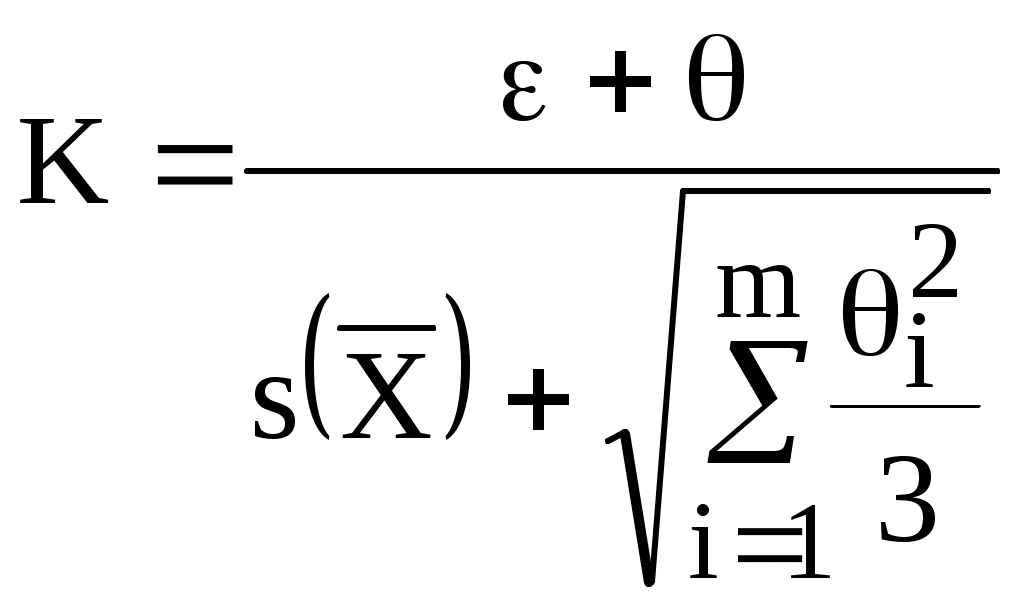