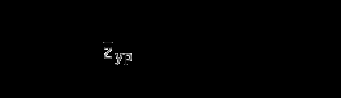Метрология. Учебное пособие. 2006 г. Введение 2 Глава измерение физических величин 4 Объекты измерений 4

• Название: Учебное пособие. 2006 г. Введение 2 Глава измерение физических величин 4 Объекты измерений 4
• Анкор: Метрология
• Дата: 18.05.2022
• Размер: 1.42 Mb.
• Имя файла: Lektsii_metrologia.doc
• Тип: Учебное пособие; #537377
• страница: 6 из 11

2.2. Статические и динамические характеристики средств измерений

Характеристики средств измерений при статических измерениях

При статических измерениях значения входного и выходногосигналов средств измерений не изменяются во времени. К статическим характеристикам средства измерения относят функцию преобразования, номинальное значение меры, диапазон и пределы измерений, цену деления шкалы, чувствительность, порог чувствительности средств измерений и др.

Основной характеристикой средства измерения при статических измерениях является функция преобразования. Она устанавливает функциональную зависимость информативного параметра выходного сигнала Y от информативного параметра входного сигнала Х средства измерения. Функция преобразования описывается в общем случае уравнением

.(2.1)

Функция преобразования, представленная в виде формулы, графика или таблицы, используется в рабочих условиях для определения значений измеряемой с помощью средства измерения величины по известному информативному параметру его выходного сигнала. Для первичных преобразователей информативным параметром входного сигнала является сама измеряемая величина; для промежуточных измерительных преобразователей и для вторичных показывающих приборов – это параметр входного сигнала, функционально связанный с измеряемой величиной и используемый для передачи ее значений. Соответственно, информативный параметр выходного сигнала средств измерения – это параметр, используемый для передачи информации о значении информативного параметра входного сигнала. Например, для электрических преобразователей информативным параметром выходного сигнала может являться напряжение, или сила тока, или фаза, или частота. Причем, если информативным параметром является, например, напряжение, то все остальные параметры (сила тока, фаза, частота) рассматриваются как неинформативные параметры сигнала. Для мер информативным параметром выходного сигнала является их номинальное или действительное значение.

На рис. 2.2 показаны виды функций преобразования средств измерений. За исключением специальных случаев, основное требование, предъявляемое к функции преобразования – это линейная зависимость выходной величины от входной, т.е.

Y= kX, (2.2)

где k – коэффициент преобразования, равный отношению сигнала Y на выходе измерительного преобразователя, отражающего измеряемую величину, к вызывающему его сигналу Х на входе преобразователя.
k не изменяется во всем диапазоне изменения входной величины и не изменяется во времени.



Рис. 2.2. Функция преобразования средств измерений: 1 – нелинейная; 2 – линейная; 3 – пропорциональная; Х_Н, Y_Н – нижние пределы измерений; Х_В, Y_В – верхние пределы измерений
Функция преобразования может быть представлена формулой, таблицей, графиком. Различают номинальную и реальную функции преобразованиясредств измерений. Для данного типа средств измерений функция преобразования является номинальной. Реальная функция преобразования конкретного экземпляра средства измерения отличается в большей или меньшей мере от номинальной. Это отличие и определяет погрешность данного средства измерения (подробнее – см. в п. 3.5 «Погрешности средств измерений»). Поэтому в технической документации на средства измерений устанавливают область допускаемых отклонений реальной функции преобразования от номинальной.

Для однозначных или многозначных мер вместо функции преобразования нормируют номинальные или индивидуальные значения мер.

Для показывающих измерительных приборов принято использовать ряд характеристик, сущность большинства из которых легко установить из рис. 2.3.



Рис. 2.3. Внешний вид отсчетного устройства вольтметра
Диапазон показаний – это область значений шкалы, ограниченная конечным и начальным значениями шкалы. Диапазон измерений – это область значений измеряемой величины на шкале прибора, в пределах которой нормированы допускаемые погрешности средств измерений (т.е. это рабочая частьшкалы). В частном случае указанные диапазоны могут совпадать, как например, на рис. 2.3.Верхний предел измерений – это наибольшее значение диапазона измерений. Нижний предел измерений – это наименьшее значение диапазона измерений.

Таким образом, диапазон измерений определяется разностью значений верхнего и нижнего пределов измерений (Х_В – Х_Н; Y_B – Y_Н).

Ценой деления называют разность значения величины, соответствующих двум соседним отметкам шкалы. Физически цену деления определяют количеством единиц входной величины, содержащихся в одном делении шкалы измерительного прибора.
Для количественной оценки влияния на выходной сигнал средства измерения входного сигнала в произвольной точке функции преобразования служит чувствительность S. Чувствительность – это свойство средства измерений, определяемое отношением изменения выходного сигнала этого средства к вызывающему его измерению измеряемой величины.

. (2.3)

Графически S определяется тангенсом угла наклона касательной (рис. 2.2), проведенной к выбранной точке Астатической характеристики. Если статическая характеристика измерительного прибора нелинейна (кривая 1 на рис. 2.2), то его чувствительность будет различной в разных точках характеристики, а шкала прибора – неравномерной. Приборы с линейной (прямая 2на рис. 2.2) или пропорциональной (прямая 3на рис. 2.2) статическими характеристиками имеют неизменную в любой точке шкалы чувствительность и равномерную шкалу.

Иногда считают, что чувствительность – это величина, обратная цене деления. Это верно только в том случае, когда шкала равномерная. В случае, когда шкала неравномерная, но цена деления по всей шкале не изменяется, а чувствительность может изменяться в несколько раз. Например, если в начале шкалы длина деления равна 1 мм, а в конце 4 мм, то при неизменной цене деления чувствительность прибора в конце шкалы будет в четыре раза больше, чем в начале.

Порог чувствительности (порог реагирования) средства измерения – это наименьшее значение изменения величины, начиная с которого может осуществляться ее измерение данным средством. Как правило, наблюдатель, осуществляющий измерение, уверенно может заметить смещение стрелки на половину деления шкалы, поэтому порог чувствительности можно считать равным половине цены деления.

Эту характеристику (порог чувствительности) было бы точнее назвать «порогом нечувствительности» прибора. Это действительно порог: стоит измеряемой величине измениться чуть меньше, и мы уже не обнаружим этого изменения по указателю прибора, он будет для нас неподвижным. Эта неподвижность может быть кажущейся: перемещение есть, но глаз человека его не улавливает. С помощью лупы можно обнаружить перемещение, соответствующее меньшему изменению измеряемой величины. Таким образом, можно снизить порог нечувствительности. Однако неподвижность может быть и действительной. Например, изменение измеряемой величины настолько мало, что силы, развиваемые в измерительном механизме, не могут преодолеть противодействующие силы, в первую очередь, силы трения. Сказанное справедливо для любого измерительного прибора с любым способом отсчета, а не только связанного с механическим перемещением подвижной части и указателя.

Не следует смешивать понятия чувствительности и порога (не)чувствительности. Например, если измеряемой величиной является длина, то значение чувствительности будет выражаться безразмерным числом, а порог чувствительности – единицей длины.

Динамические характеристики средств измерений, обусловленные инерционностью средств измерений

При статических измерениях, как было сказано выше, выходной сигнал средства измерения в точности соответствует выходному и, следовательно, коэффициент преобразования k равен номинальному коэффициенту k_о во всем диапазоне изменения входной величины Х и не изменяется во времени t, а функция преобразования имеет вид Y (t) = k_oX(t) и соответствует идеальному безынерционному линейному преобразованию.

Реальные средства измерений обладают инерционными (динамическими) свойствами, обусловленными особенностями используемых элементов. Практически все средства измерений имеют в своем составе такие инерционные элементы как подвижные механические узлы, электрические или пневматические емкости, индуктивности, элементы, обладающие тепловой инерцией и т.п. Наличие инерционных элементов определяет инерционность всего средства измерений в целом. Это приводит к тому, что мгновенное значение выходного сигнала средства измерений зависит не только от мгновенного значения входного сигнала, но и от любых изменений этого сигнала, т.е. от его первой и второй производных и производных более высокого порядка. Это приводит к более сложной зависимости между входным и выходным сигналами. Свойства средств измерений в этом случае описывают совокупностью динамических характеристик.

По степени полноты описания инерционных свойств динамические характеристики средств измерений подразделяют на полные и ча­стные. К полным динамическим характеристикам относят дифференциальные уравнения, описывающие работу средств измерений; передаточная функция; переходная характеристика; импульсная характеристика; амплитудно-фазовая и амплитудно-частотная характеристики. К частным динамическим характеристикам относят время реакции, погрешность датирования отсчета и др. Рассмотрим их подробнее.
Динамические характеристики

Дифференциальные уравнения наиболее полно описывают динамические свойства средств измерений. Общий вид уравнения с нулевыми начальными условиями:



(2.4)

где Y() и Х()– выходной и входной сигналы средств измерений как функции времени t; n - число, определяющее порядок производной, а_i и К_j – постоянные коэффициенты.

В подавляющем большинстве случаев динамическая характеристика средств измерений в линейной части функции преобразования (для средств измерений с линейной статической характеристикой во всем диапазоне преобразований) может быть приведена к уравнению вида:

(2.5)

Порядок уравнения (2.4) бывает довольно высоким, по крайней мере, выше второго. Его решение даже при известном виде функции Y(τ) весьма затруднено, а неизвестное аналитическое выражение для Y(τ) делает определение производных совершенно невозможным. Дифференциальное уравнение высокого порядка может быть представлено системой дифференциальных уравнений первого и второго порядков. Такой подход означает представление сложного в динамическом смысле средства измерения совокупностью более простых, хорошо изученных динамических звеньев (нулевого, первого и второго порядков). Например, элемент нулевого порядка описывают уравнением (2.4), динамический элемент первого порядка уравнением:

, (2.6)

где Т – постоянная времени.
Уравнение (2.5), используя преобразование Лапласа, можно записать в виде:

( )Y(p) = , (2.7)

где Y(p) и Х(p)– изображение по Лапласу выходного и входного сигналов средства измерения. Их отношение является передаточной функцией W(p)

. (2.8)

Тогда уравнение (3.7) с учетом (3.8) может быть приведено к виду:

. (2.9)
Передаточную функцию W(p)можно рассматривать как коэффициент преобразования средств измерений в динамическом режиме. Передаточная функция, как и дифференциальное уравнение, является исчерпывающей характеристикой инерционных свойств средств измерения. Она позволяет определять реакцию средства измерения на входные сигналы, изменяющиеся во времени по любому закону. В общем случае, когда входной сигнал представляет собой случайную функцию времени (т.е. случайный процесс), для оценки динамической составляющей инструментальной погрешности используют передаточную функцию прибора.

Передаточную функцию средств измерений удобно использовать при анализе работы средств измерений в автоматических системах регулирования. Ее определяют обычно через переходную характеристику h(),которая определяется как изменение во времени выходного сигнала измерительного устройства Y() при подаче на его вход скачкообразного сигнала, равного по значению единице входной величины. Если высота скачкообразного входного сигнала не равна единице, а имеет некоторое значение Х_А, то по переходной характеристике можно определить выходной сигнал, используя выражение
.(2.10)
Переходная характеристика описывает инерционность средства измерения, обусловливающую запаздывание и искажение выходного сигнала относительно входного. Ее определяют либо опытным путем, либо решая соответствующее дифференциальное уравнение (2.10).

Импульсная переходная характеристика g(τ) – это временная характеристика средства измерения, полученная в результате приложения к его входу сигнала в виде дельта-функции. Переходная и импульсная переходная характеристики связаны между собой уравнением

. (2.11)

Как и дифференциальное уравнение, эти характеристики в полной мере определяют динамические свойства средства измерения.

К частотным характеристикам относятся амплитудно-фазовая, амплитудно-частотная и фазочастотная характеристики. Частотные методы анализа основаны на исследовании прохождения гармонических колебаний различных частот через средство измерения. Если на вход линейного средства измерения подать входной сигнал , то ему будет соответствовать выходной сигнал .

Амплитудно-фазовой характеристикой G(jω) называют отношение

. (2.12)

Она описывает изменение показаний средства измерения при изменении частоты входного сигнала и характеризует только установившийся режим его работы.

Амплитудно-частотная характеристика А(ω) представляет собой зависящее от круговой частоты отношение амплитуды выходного сигнала линейного средства измерения в установившемся режиме к амплитуде входного синусоидального сигнала

. (2.13)

Фазочастотная характеристика φ(ω) – зависящая от частоты разность фаз между выходным сигналом и входным синусоидальным сигналом линейного средства измерения в установившемся режиме.

Помимо рассмотренных полных характеристик часто используют частные. Частными динамическими характеристиками могут быть от­дельные параметры полных динамических характеристик или ха­рактеристики, не отражающие полностью динамических свойств средств измерений, но достаточные для выполнения измерений с требуемой точностью. К частным динамическим характеристикам относится, например, время реакции (т.е. время установления выходного сигнала), погрешность датирования отсчета.
Типичные переходные процессы

Для определения инерционных свойств средств измерений по переходным характеристикам обычно используют заимствованное из теории автоматического регулирования понятие динамического звена. Переходные характеристики и передаточные функции типовых динамических звеньев известны, и это позволяет по форме переходной характеристики средств измерений отождествить его с каким-либо типовым динамическим звеном, а, следовательно, определить форму передаточной функции испытываемого средства измерения. Описанную процедуру принято называть идентификацией.

На рис. 2.4 показаны наиболее типичные для средств измерений формы переходных характеристик, т.е. кривые переходных процессов, или кривые разгона. Для их получения в нулевой (для простоты) момент времени входной сигнал средства измерения скачком изменяется на Х_А от некоторого значения Х₁ до Х₂ (рис. 2.4, а). По окончании переходного процесса выходной сигнал средства измерения изменяется на Y_А от значения Y₁ до Y₂.

Для определения коэффициента преобразования k средства измерения достаточно вычислить отношение Y_А/Х_А.

а)	г)
б)	д)
в)	е)

Рис. 2.4. Типичные формы переходных процессов для средств измерений: а – скачкообразное изменение входного сигнала, б – типовое усилительное звено, в – апериодическое 1-го порядка звено, г – колебательное звено, д – соединение звенев чистого запаздывания и апериодического, е – соединение звенев чистого запаздывания и колебательного.

Переходные процессы, показанные на рис. 2.4, соответствуют типовым звеньям: безынерционному усилительному (рис. 2.4, б), апериодическому первого порядка (рис. 2.4, в) и колебательному (рис. 2.4, г).

Процесс, представленный на рис. 2.4, б, характерен для электронных средств измерений, а процессы, представленные на рис. 2.4, в, г, – для большого числа средств измерений, основанных на прямом преобразовании. К группе средств измерений, представляющих собой инерционное звено первого порядка относятся средства измерений температуры и приборы теплового действия (термоанемометры, тепловые расходомеры), турбинные расходомеры. Кривая на рис. 2.4, в представляет собой экспоненту, а величина Т(подкасательная) – постоянную времени. Она определяет время, за которое выходной сигнал достиг бы нового установившегося значения, если бы изменялся с постоянной скоростью, равной скорости в момент скачкообразного изменения входного сигнала.

Постоянную времени Т используют для характеристики динамических свойств средств измерений. Поскольку проведение касательной кривой переходного процесса (графический метод) сопряжено с погрешностями, значения постоянной времени определяют как интервал времени, за который выходной сигнал изменяется на 0,632 от своего приращения y_a (рис. 2.4, в).

Колебательное динамическое звено, а следовательно, и средство измерения, в котором имеет место переходный процесс (рис. 2.4, г), можно рассматривать как соединение двух апериодических звеньев с постоянными времени Т₁ и Т₂. При этом в зависимости от соотношений Т₁ и Т₂переходный процесс будет различен. Если (Т₁/Т₂)<2, то он имеет форму кривых 1 и 2, апри (Т₁/Т₂) 2 - форму кривой 3(рис. 3.4, г).

Переходные процессы, показанные на рис. 2.4, д, е, характерны для случаев, когда дифференциальное уравнение, описывающее динамику средства измерения, имеет порядок более чем второй. В этих случаях принято рассматривать средства измерений как совокупность нескольких, соединенных последовательно типовых динамических звеньев. Например, средство измерения с переходным процессом, показанным на рис. 2.4, д, можно рассматривать как соединение звена чистого запаздывания со временем запаздывания _з и апериодического звена с постоянной времени Т(для графического определения значений _з и Тдостаточно провести касательную к точке перегиба Ана рис. 2.4, д). Измерительное устройство с переходным процессом, показанным на рис. 2.4, е, можно рассматривать как соединение звена чистого запаздывания и колебательного звена.

Для всех средств измерений важным является время установления выходного сигнала (или показаний)t_p (рис. 2.4), которое также называют временем реакции. Оно определяет собой отрезок времени, необходимый для завершения переходного процесса при скачкообразном изменении входного сигнала. Так как все рассмотренные переходные процессы (рис. 2.4) теоретически заканчиваются только при бесконечном значении времени, то за время реакции t_pобычно принимают время, в течение которое выходной сигнал средства измерения, приближаясь к новому установившемуся значению, входит в некоторую зону, отличающуюся от этого значения на ±5 % от изменения выходного сигнала, соответствующего данному скачкообразному входному сигналу.

Значение времени реакции может быть приближенно определено через постоянную времени средства измерения из соотношения
t_p = (3  5)Т. (2.14)

В большинстве средств измерений реализуется блочно-модульный принцип их построения, что обеспечивает возможность создания различных функционально сложных устройств из ограниченного числа простых унифицированных блоков и модулей путем их наращивания и стыковки. Такой подход обеспечивает получение всего многообразия измерительной информации о физических величинах, характеризующих технологические процессы, свойства и качество продукции. Внутри средства измерения при этом осуществляются различные процессы по преобразованию входных измерительных сигналов и превращению их в выходные в зависимости от устройства средства измерения, определяемого структурной схемой.

Структурные схемы средств измерений

Структурная схема – это условное обозначение совокупности элементов средства измерения, образующих непрерывный путь прохождения измерительного сигнала от входа до выхода и обеспечивающих осуществление всех его преобразований, с указанием преобразуемых величин. При этом каждое преобразование сигнала происходит в отдельном звене или блоке. Структурные схемы состоят из соединенных определенным образом структурных элементов (составных частей), предназначенных для выполнения одной из следующих функций:

- преобразование поступающего сигнала по форме или виду энергии;

- успокоение колебаний;

- защита от помехонесущих полей;

- коммутация цепей;

- представление информации и т.п.

Основными составными частями средства измерения являются:

преобразовательный элемент – элемент средства измерения, в котором происходит одно из ряда последовательных преобразований величины;

измерительная цепь (измерительный канал) – совокупность элементов средства измерения, образующих непрерывный путь прохождения сигнала измерительной информации от входа до выхода;

чувствительный элемент – часть измерительного преобразователя в измерительной цепи, воспринимающая входной измерительный сигнал;

измерительное устройство – часть измерительного прибора, связанная с сигналом измерительной информации и имеющая обособленную конструкцию и назначение (например, регистрирующее устройство измерительного прибора, включающее ленту для записи, лентопротяжный механизм и пишущий элемент);

показывающее устройство – совокупность элементов средства измерений, обеспечивающих визуальное восприятие значений измеряемой величины или связанных с ней величин (цифровое табло или шкала с указателем);

регистрирующее устройство – совокупность элементов средства измерений, регистрирующих значения измеряемой или связанной с ней величины.

Для удобства анализа различных соединений средств измерительной техники между собой и со средствами автоматического управления их принято рассматривать как некоторый преобразователь, служащий для преобразования входного сигнала X в выходнойY. Это позволяет применять при анализе систем хорошо разработанный аппарат теории автоматического регулирования. На структурных схемах элементы изображают в виде прямоугольников, внутри которых обозначено каким-либо образом их название, Кроме того, на схеме обязательно должно быть показано направление распространения измерительной информации, т.е. обозначены входы и выходы структурных элементов. Часто приводят поясняющие надписи, временные зависимости сигналов в характерных точках и т.п.

На рис. 2.5 приведены структурные схемы средств измерений (измерительных приборов и преобразователей) прямого действия (рис. 2.5, а, в) и сравнения (рис. 2.5, б, г).Первые часто называют средствами измеренияпрямого преобразования, а вторые – средствами измерения уравновешивающего (или компенсационного) преобразования.

а)

б)

в)

г)

1 – чувствительный элемент, 2, 5, 6, 7 – преобразовательные элементы, 3 – измерительное устройство, 4 – показывающее устройство
Рис. 2.5. Структурные схемы средств измерений: а – измерительного прибора прямого действия, б – измерительного прибора сравнения, в – измерительного преобразователя прямого действия, г – измерительного преобразователя сравнения
Структурная схема измерительного прибора или преобразователя однозначно определяется используемым методом преобразования.

Измерительный прибор, основанный на методе прямого преобразования (рис. 2.5, а),работает следующим образом. Измеряемая величина Xпоступает в чувствительный элемент 1, где преобразуется в другую физическую величину, удобную для дальнейшего использования (например, ток, напряжение, давление, перемещение, сила), и поступает на промежуточный преобразовательный элемент 2, который обычно либо усиливает поступающий сигнал, либо преобразует его по форме (в частном случае элемент 2может отсутствовать). Выходной сигнал элемента 2поступает к измерительному устройству 3,перемещение элементов которого определяется с помощью показывающего устройства 4. Выходной сигнал (показание) воспринимается органами чувств человека, который считывает показание с показывающего устройства. В качестве указателя на показывающем устройстве может быть подвижная стрелка, луч света, перо самописца и др.

Показаниемназывают значение величины или число на показывающем устройстве средства измерения, выраженное в принятых единицах этой величины (на рис. 2.3 показание равно 65 В).

Здесь сигнал Z, возникающий на выходе чувствительного элемента 1, поступает на преобразовательный элемент 5, который способен осуществлять сравнение двух величин, поступающих на его вход. Кроме величины Z на выход элемента 5 подается с противоположным знаком величина Z_yp (уравновешивающий сигнал), которая формируется на выходе обратного преобразовательного элемента 6. На выходе элемента 5 формируется сигнал, пропорциональный разности значений величин Z и Z_yp. Этот сигнал поступает в промежуточный преобразовательный элемент 2, выходной сигнал которого поступает одновременно на измерительное устройство 3и на вход обратного преобразовательного элемента 6. В зависимости от типа промежуточного преобразовательного элемента 2при каждом значении измеряемого параметра и соответствующем ему значении Z разность Z – Z_yp, поступающая на вход элемента 5, может сводиться к нулю или иметь некоторое малое значение, пропорциональное измеряемой величине.

На рис. 2.5, в, гприведены структурные схемы измерительных преобразователей, основанных соответственно на методах прямого и уравновешивающего преобразования. В этих схемах отсутствуют измерительное и показывающее устройство, поскольку сигнал измерительных преобразователей имеет форму, недоступную для восприятия человеком. В то же время в составе измерительных преобразователей, как правило, имеется конечный преобразовательный элемент 7, который формирует выходной сигнал (усиливает его по мощности, преобразует в частоту колебаний и т.д.) таким образом, что его можно передавать на расстояние, хранить и обрабатывать.

Схемы средств измерений зачастую могут быть комбинированными, т.е. содержать цепь прямого преобразования, звенья которой охвачены отрицательной обратной связью. При этом принцип построения структурной схемы влияет на многие его параметры, динамические и другие характеристики средства измерения, которые, в свою очередь, определяют степень соответствия информации об измеряемой величине ее истинному значению.