Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124

• Название: Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
• Дата: 09.01.2023
• Размер: 1.57 Mb.
• Имя файла: posobie_f.docx
• Тип: Учебное пособие; #878255
• страница: 16 из 27

работа, мощность, энергия. Закон сохранения и изменения механической энергии

(Задачи: 6.6; 7.6; 8.6; 8.6; 10.6; 11.6; 12.6; 13,6; 13.6; 14.6; 15.6; 16.6; 17.6; 18/6; 19.6; 20.6; 1. 6; 2.6; 3.6; 4.6; 5.6.)

При решении задач единого государственного экзамена на работу, мощность и энергию необходимо знать следующие законы и определения. Во-первых, это определения всех перечисленных величин, причем глубокого понимания того, что такое потенциальная энергия, в общем - то, не требуется: достаточно помнить формулы потенциальных энергий тела в однородном поле тяжести и деформированной пружины. Определение работы достаточно знать только для постоянной силы и помнить формулу для работы силы упругости. Во-вторых, необходимо знать и уметь применять в простейших случаях теорему об изменении кинетической энергии. И, в-третьих, нужно знать закон сохранения механической энергии, а также понимать, в каких случаях этот закон выполняется, а когда нарушается.

Сформулируем эти определения и законы.

Кинетической энергией тела массой m , движущегося со скоростью v, называется величина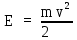

(6.1)

Пусть тело при своем движении совершает перемещение 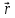. Если в процессе этого движения на тело действует постоянная сила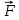 , то работой этой силы называется величина

A = Frcos α,

где α - угол между векторами силы и перемещения.

Если в процессе движения тела сила изменяется, для вычисления работы необходимо разбивать траекторию на такие малые участки, что силу или угол на каждом из них можно считать постоянными, находить работу силы на каждом участке, а затем суммировать.

Если на тело действуют несколько сил, то работа, совершенная равнодействующей силой, равна сумме работ, совершенных отдельными силами.

Все силы в природе можно разделить на две группы - потенциальные и непотенциальные. К непотенциальные силам относятся силы сопротивления или трения, к потенциальным - все остальные.

Для вычисления работ, которые совершают потенциальные силы, вводится понятие потенциальной энергии. Потенциальной энергией тела называется такая функция координат, разность значений которой для начала и конца траектории равна совершенной работе. Для решения задач школьного курса физики необходимо знать, что потенциальная энергия тела в поле силы тяжести равна

U = ± mgh, (6.3)

где m - масса тела, g - ускорение свободного падения, h - высота расположения тела по отношению к некоторому уровню, который считается начальным (может быть выбран любым). Знак «+» в этой формуле следует взять, когда тело находится выше начального уровня, знак «-», если ниже.

Потенциальная энергия сжатой, или растянутой пружины определяется соотношением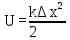

(6.4)

где k- коэффициент жесткости пружины, Δx - ее деформация. Следует иметь в виду, что эта формула справедлива независимо от того, сжата пружина или растянута. Следует также помнить, что для непотенциальные сил ввести потенциальную энергию нельзя.

Через изменение потенциальной энергии можно найти работу соответствующей силы. Если, например, тело переместилось из точки, в которой его потенциальная энергия равнялась U₁, в точку, в которой его потенциальная энергия равняется U₂, то отвечающая этой потенциальной энергии сила совершила работу

A = U₁ - U₂. (6.5)

Если некоторая сила F совершает работу А за время Δt, то мощностью этой силы N называется отношение

N = 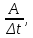(6.6)

которое имеет смысл работы, совершаемой в единицу времени. В связи с формулой (6.6) можно говорить о средней или мгновенной мощности, когда интервал времени Δt стремится к нулю.

Для любого движения тела справедливо утверждение, которое называется теоремой об изменении кинетической энергии: изменение кинетической энергии тела равно сумме работ всех сил, действующих на тело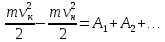

(6.7)

где v_Hи v_K - скорости тела в начале и конце некоторого участка пути, A₁, A₂,... - работы всех сил, действующих на тело. Рассматриваемый в теореме (6.7) участок пути может быть выбран произвольно, но работы должны вычисляться именно на этом участке. Теорема об изменении кинетической энергии позволяет находить начальную или конечную скорость тела (при известных работах), либо работу какой-то силы (при известных скоростях).

Теорему об изменении кинетической энергии можно сформулировать и на другом языке. Если на тело действуют только потенциальные силы, то их работу можно выразить через разности начальной и конечной потенциальной энергий. Тогда уравнение (6.7) можно представить в виде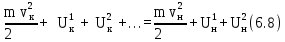



где 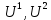- потенциальные энергии сил, действующих на тело (в начальном и конечном положениях тела). Сумма Кинетической и потенциальной энергии тела называется его механической энергией. Из формулы (6.8) заключаем, что если на тело действуют только потенциальные силы, его механическая энергия не изменяется. Формула (6.8) называется законом сохранения механической энергии. Если на тело действуют и непотенциальные силы, то механическая энергия не сохраняется, но ее приращение равно работе непотенциальные сил.

Разберем на основе этих определений и законов приведенные задачи.

1). В задаче 6.6 из формул для величины импульса и кинетической энергии

p = mv, 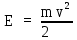получаем m= р²/2Е, откуда находим m = 1 кг

(ответ - 2).

2). Задача 7.6. Из формулы для кинетической энергии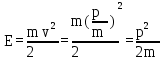

заключаем, что размерность квадрата импульса, деленная на размерность массы, дает размерность энергии, т.е. Джоуль. Обратим внимание читателя, что названия всех единиц измерений, данные в ответах к этой задаче, представляют собой фамилии выдающихся физиков.

(ответ- 1).

3). Задача 8.6. Поскольку плита поднимается медленно, сила, с которой трос действует на плиту, равна силе тяжести. Поэтому работа, которую совершает подъемный кран, равна изменению потенциальной энергии тела mgh = 2,5 ·10⁴ Дж,

где m - масса плиты, g - ускорение свободного падения, h - высота подъема.

(ответ - 2).
В задачах по физике часто приходится вычислять работу, которую совершает над каким-то телом сила тяжести. Следует запомнить, что независимо от траектории тела эта работа равна ± mgh, где m - масса тела, g - ускорение свободного падения, h - разность уровней начального и конечного положения тела. Знак «+» в этой формуле следует взять, когда тело спускается (начальное положение выше конечного), знак «-», если поднимается. Например:

4). В задаче 9.6 тело массой 2 кг спускается на расстояние (по вертикали) 3 м. Поэтому сила тяжести совершает работу А = 2кг·10м/с²·3м = 60 Дж.

(ответ - 2).

5). Задача 10.6. Из формулы (6.3) для потенциальной энергии силы тяжести заключаем, что потенциальная энергия мяча увеличивается на 12 Дж.

(ответ- 2).

6). Задача 11.6. Человек массой m = 70 кг, поднявшись на пятый этаж (h = 15 м), совершает работу не меньше, чем А = mgh = 10500 Дж. Поскольку человек затрачивает на подъем время t = 14 с, то средняя мощность, развиваемая этим человеком, равна N = 10500/14 = 750 Вт. Переводя это значение в лошадиные силы, заключаем, что средняя мощность, развиваемая человеком в течение рассматриваемого интервала времени, примерно равна одной лошадиной силе. Конечно, подняться на пятый этаж за 14 с непросто, но вполне возможно для тренированного человека.

(ответ 4).

7). Задача 12.6. Поскольку тело поднимается равномерно, сила, действующая на тело со стороны троса, равна силе тяжести. Поэтому мощность, развиваемая лебедкой, равна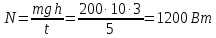



(ответ – 3)

8.) Задача 13.6.поскольку при движении тела по шероховатой горизонтальной поверхности сила трения не изменяется, работа силы трения равна

А = -µmgS,

где µ. - коэффициент трения, m - масса тела, g - ускорение свободного падения,S - пройденный путь. Знак «-» в этой формуле есть следствие противоположных направлений силы трения и скорости тела. Согласно этой формуле получим А = -10 Дж.

(ответ - 4).

9). Задача 14.6. Пусть на тело, движущееся со скоростью v, начинает действовать некоторая сила, которая останавливает это тело. Тогда из теоремы об изменении кинетической энергии заключаем, что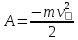

,

где А- работа этой силы. Отсюда следует, что работа, которую нужно совершить, чтобы остановить тело, пропорциональна квадрату его скорости.

(ответ- 3).

10). Задача 15.6. Аналогично находим, что работа силы трения равна А = -1Дж

(ответ - 1).

11). В задаче 16.6 используем теорему об изменении кинетической энергии для рассматриваемого в условии груза



где А_mg - работа силы тяжести, A_F - работа данной силы F . На участке пути 3 м эти силы совершают над грузом работы

A_mg = -1·10·3 = -30 Дж, А_F =50·3 = 150 Дж.

Отсюда заключаем, что изменение кинетической энергии тела равно 120 Дж.

(ответ - 2).

12). Задача 17.6. Формулу для работы, совершаемой силой упругости, нужно запомнить.

Если пружина растягивается или сжимается из недеформированного состояния, то сила упругости совершает работу

( ответ в - 4).

13). Задача 18.6. Используя формулу (6.4) для потенциальной энергии пружины, находим энергию пружины, растянутой на величину Δl:

Е₁ = ,

и сжатой на величину Δl/2:

Е₂ = .

Вычитая вторую величину из первой, находим, что потенциальная энергия пружины, растянутой на величину Δl, больше на

,

чем потенциальная энергия этой же пружины, сжатой на величину Δl/2

(ответ- 2).

14). Задача 19.6. При столкновениях тел механическая энергия может сохраняться (в этом случае говорят об абсолютно упругом столкновении), а может и не сохраняться (неупругое столкновение). В этом случае механическая энергия переходит в другие формы, и в частности, в тепло.

При этом согласно закону сохранения энергии количество выделившейся теплоты равно разности начальной и конечной механической энергии тела. Поэтому получаем



где Е_н и Е_к - начальная и конечная кинетические энергии мяча, v_н и v_к - начальная и конечная скорости мяча.

Подставляя в эту формулу данные условия, получаем

Q = 0,375 Дж.

(ответ - 4).

15). Задача 20.6. Пусть при торможении автомобиля его скорость снизилась от v до v/2. Тогда по теореме об изменении кинетической энергии имеем

,

где S - тормозной путь автомобиля при таком торможении, F_Tp -сила трения, действующая на тело.

Если скорость автомобиля снижается от v/2 до нуля, теорема об изменении кинетической энергии дает

=-

Отсюда заключаем, что тормозной путь S в первом случае больше тормозного пути S₁во втором в 3 раза.

(ответ - 3).

16). Задача 1.6. При бросании тела со скоростью v₀ под углом α к горизонту его начальная кинетическая энергия равна



Скорость в верхней точке траектории равна

v₀cosα,

и потому кинетическая энергия в верхней точке

.

Отсюда по теореме об изменении кинетической энергии находим работу силы тяжести

.

(ответ – 1)

17). Задача 2.6. До попадания тела на ленту транспортера тело имело кинетическую энергию 0,5Дж, после остановки относительно ленты - 4,5 Дж, причем единственной силой, которая совершала работу (изменила скорость тела) является сила трения между телом и лентой.

Поэтому по теореме об изменении кинетической энергии получаем

А_тр = - 4 Дж

(ответ - 1).

18). Задача 3.6. Запишем для участка движения тела от начала контакта с пружиной до остановки закон сохранения механической энергии



Здесь нуль в левой части - это потенциальная энергия недеформированной пружины (до момента контакта тела с пружиной), а нуль в правой части - кинетическая энергия тела в момент остановки (именно это положение тела отвечает максимальному сжатию пружины).

Отсюда находим

.

(ответ– 1)

19). Задача 4.6. является достаточно сложной для школьников, поскольку правильный ответ (который мгновенно получается по теореме об изменении кинетической энергии

) кажется бессмысленным.

С одной стороны, раз А= 0, то стенка ничего «не делала», с другой стороны, понятно, что именно она останавливала тело. Тем не менее, этот ответ правильный, а стенка совершала работу дважды.

Сначала она остановила тело (т.е. изменила его скорость от v до нуля) и совершила работу

А =- mv²/2,

затем разогнала - от нулевой скорости до v и совершила при этом работу

А =mv²/2.

Поэтому суммарная работы силы, действующей на тело со стороны стенки, равна нулю.

В этом решении ярко проявляется невекторный (скалярный) характер энергии: кинетическая энергия тела, движущегося в направлении стенки и от нее, одинакова.

(ответ- 4)

20). В задаче 5.6. необходимо найти мгновенную мощность, развиваемую силой тяжести.

Пусть в некоторый момент времени тело имеет скорость v. Тогда за малый интервал времени Δt, за который его скорость не успевает измениться, тело проходит расстояние vΔt.

Следовательно, работа силы тяжести за этот интервал времени будет равна

mgvΔt,

а мощность, развиваемая силой тяжести, -

N = А/Δt = mgv.

А поскольку для падающего из состояния покоя тела

v = gt,

получаем

N = mg²t.

Это значит, что мощность силы тяжести линейно возрастает со временем.

(ответ 3)