Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
 Скачать 1.57 Mb. Скачать 1.57 Mb.
|
|
(ответ - 1). 8) В задаче 9.2 необходимо использовать зависимость (2.3) для скорости. Так как по условию автомобиль движется из состояния покоя, проекция зависимости (2.3) на ось х, направленную вдоль вектора ускорения, имеет вид: 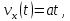 где vx- проекция вектора скорости тела на ось х. Так как vx =10 м/с в момент времени t =5 с, находим а = vx /t = 2 м/с2. (ответ - 2). 9) Задача 10.2. Сравнивая данную зависимость координаты от времени x(t) = 8t - 2t2 с законом (2.2), заключаем, что начальная скорость тела v0х = 8 м/с, проекция ускорения тела на ось ОХ - ах = -4 м/с2. Поэтому из (2.3) получаем зависимость скорости тела от времени: (ответ -2) 10). Задача 11.2. Зависимость проекции скорости от времени на ось, направленную вертикально вверх, имеет вид: vx(t) = v0 - gt где v0 = 10 м/с - начальная скорость тела. Подставляя в эту формулу время t = 0,5 с, находим скорость тела через 0,5 с после броска vx =5 м/с. Знак «плюс» для проекции скорости на рассматриваемую ось показывает, что через 0,5с после броска вектор скорости тела все еще направлен вверх. (ответ - 3) 11) Задача 12.2. Чтобы найти время подъема тела, брошенного вертикально вверх, на максимальную высоту используем то обстоятельство, что в верхней точке траектории скорость тела равна нулю. Поэтому подстановка времени подъема τ в зависимость скорости от времени дает 0 = v0 - gτ где v0- начальная скорость тела. Отсюда получаем для времени подъема: τ = v0/g = 1 с (ответ- 4). 12) Задача13.2. Самую максимальную высоту подъема можно найти, подставляя найденное время подъема τ в зависимость координаты тела по вертикальной оси от времени 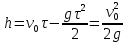 Подстановка в эту формулу числовых значений дает h = 5 м (ответ - 1). 13) Задача 14.2. Пусть время, затраченное телом на прохождение участка пути длиной S, отсчитанного от начальной точки, равно t1, а время, затраченное телом на прохождение участка пути длиной 2S, отсчитанного от этой же точки, равно t2. Тогда из уравнения движения (2.2) в проекции на ось, направленную вдоль вектора ускорения тела, имеем: 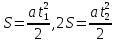 Деля первое уравнение на второе и извлекая из этого отношения квадратный корень, находим: 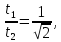 т.е время прохождения пути S меньше времени прохождения пути 2S в 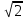 раз. раз.(ответ - 2). 14) Задача 15.2. В некоторых ситуациях приходится применять одновременно обе зависимости - и координаты и скорости. Например, в этой задаче зависимости координаты тела по вертикальной оси и проекции скорости на эту ось имеют вид: 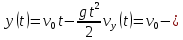 Из первой зависимости находим время, за которое тело поднимается на высоту h= 20 м 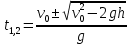 (Два корня для времени получилось, поскольку на рассматриваемой высоте тело побывало дважды - в процессе подъема и в процессе спуска.) Подставляя эти значения времени в уравнение для скорости, получим для проекции скорости на вертикальную ось на высоте h: 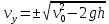 («плюс» - на подъеме, «минус» - на спуске). Отсюда находим величину скорости тела на этой высоте - 15 м/с (ответ - 3). Иногда в задачах на равноускоренное движение требуется найти интервалы времени или расстояния, отсчитанные не от момента начала движения или от начального положения тела. Трудность таких задач заключается в том, что такие времена или расстояния сами не входят в уравнения равноускоренного движения. В этом случае искомые интервалы времени или расстояния удобно находить как разность интервалов времени или расстояний, отсчитанных от начала движения. 15) Задача 16.2. Зависимость координаты автомобиля от времени дается соотношением 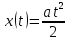 где а = 2 м/с2 - ускорение автомобиля, в качестве начала координат выбрана точка начала движения. Из этой зависимости находим, что через 2 с после начала движения автомобиль окажется на расстоянии 4 м от начальной точки, через 3 с после начала движения- на расстоянии 9 м от начальной точки. Поэтому за третью секунду движения автомобиль пройдет путь 5м. (ответ - 3). 16) В задаче 17.2 аналогично из зависимости координаты тела от времени находим, что автомобиль окажется на расстоянии 2м от начальной точки через время 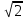 с, на расстоянии 3м - через время с, на расстоянии 3м - через время 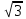 с. Поэтому на прохождение третьего метра пути автомобиль затратит время с. Поэтому на прохождение третьего метра пути автомобиль затратит время 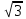 - - 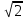 с. с.(ответ - 2). 17) В задаче 18.2 следует из зависимости скорости от времени найти время падения, а затем подставить его в зависимость координаты от времени. (ответ - 1.) 18) Задача 19.2. При движении тела под углом к горизонту вектор ускорения тела направлен вертикально вниз (ускорение свободного падения - g). Поэтому проекция зависимости скорости от времени (2.3) на горизонтальную ось имеет вид: 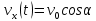 где v0- начальная скорость тела, α - угол, под которым бросили тело (проекция вектора ускорения тела на горизонтальную ось равна нулю). Из этой формулы следует, что проекция скорости на горизонтальную ось не зависит от времени. (ответ - 4). 19) Задача 20.2. Дальность полета тела, брошенного под углом к горизонту, определяется из проекции уравнения (2.2) на горизонтальную ось: l = v0cosα где v0cosα - проекция вектора начальной скорости на горизонтальную ось, t- полное время движения. По условию задачи проекции векторов начальной скорости тел на горизонтальную ось одинаковы (это подчеркнуто на рисунке в условии с помощью вертикальной пунктирной прямой). Поэтому дальше улетит то из них, у которого больше время движения. А оно, в свою очередь, определяется проекцией уравнения (2.2) на вертикальную ось: 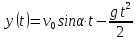 поскольку в момент падения вертикальная координата тела равна нулю. Отсюда следует, что время движения равно 2v0sinα/g, т.е. определяется проекцией вектора начальной скорости на вертикальную ось. А она по условию больше у тела 1, которое, таким образом, и улетит дальше (ответ 1). 20) Задача 1.2 содержит небольшой «подвох». При движении тела по прямой и в одном направлении пройденный путь равен разности координат конца и начала траектории. В этом случае можно, выбрав начало координат в начальной точке, найти пройденный путь, просто подставляя время в уравнение для координаты. В нашем же случае тело движется сначала вверх, потом вниз. Действительно, время подъема для тела, брошенного вертикально вверх со скоростью 20 м/с, равно 2 с. А пройденный путь нужно найти за 3с после броска. Поэтому пройденный путь складывается из максимальной высоты подъема (для тела, брошенного со скоростью 20 м/с, она равна 20 м) и длины участка пути от верхней точки траектории до точки, в которой тело окажется через 3 с после броска. Координату этой точки в системе координат, начало которой расположено на земле, а ось у направлена вертикально вверх, можно найти, подставляя это значение времени в уравнение: y(t) = 20t – 5t2 (все величины заданы в международной системе единиц СИ). В результате находим, что пройденный телом путь равен 25 м. (ответ 3). 3. Задания на проверку элементов знаний и умений по теме: динамика (законы Ньютона, сила тяжести, сила упругости, равнодействующая.) (Задачи: 3.3; 4.3; 5.3; 6.3; 7.3; 8.3;9.3; 10.3; 11.3; 12.3; 13.3; 14.3; 15.3; 16.3; 17.3; 18.3; 19.3; 20.3; 1.3; 2.3.) Задачи на динамику часто входят в задания единого государственного экзамене по физике. Для решения этих задач необходимо понимать смысл законов Ньютона, уметь применять их в простейших ситуациях и знать свойства ряда сил: тяжести, трения, упругости и нескольких других. Первый закон Ньютона определяет такие системы отсчета, в которых тело, не испытывающее воздействий со стороны других тел (сил), движется прямолинейно и равномерно. Такие системы отсчета называются инерциальными, а движение в отсутствии сил - движением по инерции. Согласно второму закону Ньютона ускорение тела а относительно инерциальных систем отсчета определяется из уравнения: m 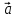 = =  1 + 1 + 2 + 2 +  3+…(3.1) 3+…(3.1)где т- масса тела,  1 + 1 +  2 + 2 +  3 +... - векторная сумма сил, действующих на тело (эту сумму часто называют равнодействующей или результирующей силой). 3 +... - векторная сумма сил, действующих на тело (эту сумму часто называют равнодействующей или результирующей силой).Третий закон Ньютона утверждает, что всегда существует взаимное действие тел друг на друга, причем силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению. Чтобы использовать уравнение (3.1) для нахождения ускорений тел необходимо задать законы для действующих на них сил. Рассмотрим ряд сил, с которыми приходится сталкиваться в школьном курсе физики. На любое тело, находящееся вблизи поверхности Земли действует сила притяжения со стороны Земли, которая называется силой тяжести. Эта сила пропорциональна массе тела и может быть записана в виде:  = m = m , (3.2) , (3.2)где  - вектор ускорения свободного падения, величина которого равна g = 9,8 м/с2 (в расчетах часто используют значение g = 10 м/с2). - вектор ускорения свободного падения, величина которого равна g = 9,8 м/с2 (в расчетах часто используют значение g = 10 м/с2).При соприкосновении тел возникают контактные взаимодействия. Сила, перпендикулярная поверхности и возникающая при контакте тела с этой поверхностью, называется силой нормальной реакции поверхности. При скольжении тела по поверхности или при попытке его сдвинуть возникает сила, параллельная поверхности, и препятствующая движению тела. Эта сила называется силой трения (сила трения подробно рассматривается в следующей главе). Если тело растягивает или сжимает пружину, на тело со стороны пружины действует сила, которая называется силой упругости. Свойства силы упругости определяются законом Гука, в котором утверждается, что сила упругости пропорциональна удлинению пружины Δх =  Fупр = kΔx (3.3) Fупр = kΔx (3.3)Здесь l - длина деформированной пружины, l0 - длина этой пружины в недеформированном состоянии, k - коэффициент пропорциональности, который называется коэффициентом жесткости (или просто жесткостью) пружины. При движении тела в воздухе, воде или в другой среде на тело со стороны этой среды действует сила сопротивления, величина которой при небольших скоростях тела пропорциональна его скорости Fсопр = αv Здесь v - скорость тела, α - коэффициент пропорциональности, зависящий от свойств среды и геометрии тела. Для больших скоростей сила сопротивления определяется формулой: Fcoпp = βv2. Направлена сила сопротивления противоположно скорости тела и тормозит его движение. Рассмотрим теперь задачи. 1) |
