Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
 Скачать 1.57 Mb.
|
|
11.Задания на проверку элементов знаний и умений по теме: Кинематика и динамика вращательного движения. (Задачи: 20.11; 2.11; 17.11; 3.11; 6.11; 13.11; 10.11; 9.11; 7.11; 5.11; 18.11; 4.11; 12.11; 19.11; 11.11; 14.11; 8.11; 16.11; 15.11; 1.11.) Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью w тела, совершающего вращательное движение, называется отношение угла поворота Δφ к тому времени Δt, за которое этот поворот произошел 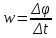 (7.1)В этом определении угол Δφ должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан - безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени Δt), так и мгновенную (при Δt→ 0) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени Δt. Применяя определение (7.1) к полному обороту тела (угол поворота - 2π радиан), получим связь угловой скорости и периода вращения Т 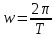 (7.2)Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела. Из формулы (7.2) легко получить связь угловой и обычной скорости v вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности R и учитывая, что 2πR - это длина пути, пройденного за период, получим 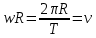 (7.3)Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными. Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью v вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна 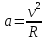 (7.4)Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах a = w2R = vw (7.5) Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса R с постоянной по величине скоростью v (и соответственно угловой скоростью w = v / R), на него должна действовать сила, направленная к центру окружности и равная по величине 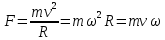 (7.6)Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации. Рассмотрим их применение к решению задач. 1). Задача 20.11. Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол 2π за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна ω = 2π рад/мин. (ответ - 2). 2).Задача 2.11. Для нахождения линейной скорости конца секундной стрелки часов используем связь угловой и линейной скоростей (7.5). Имеем 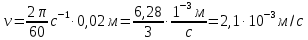 (ответ - 2). 3). Задача 17.11. Применяя определение угловой скорости к колесу, получаем 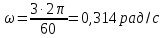 (ответ - 1). 4). Задача 3.11. Из формулы (7.2) имеем 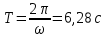 (ответ - 4). 5). Задача 6.11. Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение, из формулы (7.5) находим квадрат угловой скорости диска 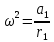 .А теперь по формуле (7.5) для второй точки получаем 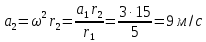 (ответ - 2). 6) Задача 13.11. Поскольку скорость автомобиля не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории. (ответ - 3). 7) Задача10.11. Ускорение мальчика будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли v = ωR . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна 2v = 2ωR. Поэтому центростремительное ускорение мальчика будет равно 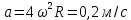 2(ответ - 4). 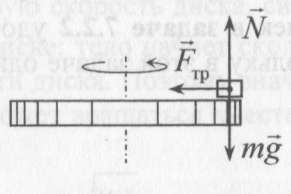 8). Задача 9.11. Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним, участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче центростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов - первые три касаются природы взаимодействий, вторые - результат действия. Поэтому правильный ответ на вопрос задачи - 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться). (ответ - 1).9). Задача 7.11. Поскольку тело вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму чакону Ньютона, туда же направлена и результирующая сила, действующая на тело. (ответ - 2). 10). Задача 5.11. Применяя к данному телу второй закон Ньютона и учитывая, что его ускорение равно 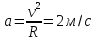 ,получим для равнодействующей F = 2 Н. (ответ 2). 11) Задача 18.11. Используя формулу для центростремительного ускорения a= v2/R, находим отношение ускорений материальных точек 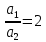 .(ответ - 1). 12). Задача. 4.11. Для сравнения центростремительных ускорений материальных точек удобно использовать формулу 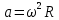 ,поскольку в этой задаче одинаковы угловые скорости точек. Получаем 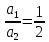 .(ответ - 3). 13). Задача 12.11. Для сравнения центростремительных ускорений выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим  Поэтому  .(ответ - 1). 14). Задача 19.11. Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки  где 2π/12 и 2π/1 - угловые скорости часовой и минутной стрелки соответственно (в рад/час), lч и lм - длины часовой и минутной стрелок. Учитывая, что lм = 2lч, получаем  (ответ - 2). 15). Задача 11.11. Телу, вращающемуся вместе с диском на его горизонтальной поверхности, центростремительное ускорение сообщается силой трения FTp = mω2R. Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения µmg. Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства mω2R ≤ µmg →  .(ответ - 4). 16). В задаче 14.11 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем Т = mω2l. (ответ - 3). 17). В задаче 8.11 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает  mω2 2l = Т.(1)На ближнее тело действуют силы натяжения T1 и Т двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем mω2l = Т1 - Т. Подставляя в эту формулу силу Т из формулы (1), находим T1= mω2l = 3T/2. (ответ - 2). 18). В задаче 16.11 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как l1 и l2. имеем l1 + l2 = l,  где v1 =1 м/с и v2 =2 м/с - линейные скорости концов стержня, l = 1 м - его длина. Решая эту систему уравнений, найдем расстояния l1 и l2, а затем и угловую скорость стержня ω=  В результате получим  .(ответ - 3). 19). Задача 15.11. Среднее ускорение тела за некоторый интервал времени Δt (не обязательно малый) определяется по формуле (2.1):  За половину периода вектор скорости поворачивается на 180°, поэтому величина разности  -  равна 2v = 4πR / Т . Поэтому среднее ускорение тела за половину периода равно  .(ответ - 1). 20). Задача 1.11. Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (ответ - 2). |