Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124

• Название: Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
• Дата: 09.01.2023
• Размер: 1.57 Mb.
• Имя файла: posobie_f.docx
• Тип: Учебное пособие; #878255
• страница: 19 из 27

(ответ - 1).

16). В задаче 3.8 умышленно дано много лишних данных. Поскольку и в воде, и в керосине мяч плавает, то архимедова сила и в том, и в другом случае уравновешивает силу тяжести мяча F = mg.

(ответ - 2).

17.) Задача 4.8. Несмотря на то, что тело не касается дна и стенок сосуда, суммарная сила, действующая на левую чашку весов, увеличится. Действительно, при опускании тела в воду возникает сила Архимеда, действующая со стороны воды на тело, но при этом и тело действует на воду, причем эта сила направлена вертикально вниз и равна силе Архимеда. Чтобы весы остались в равновесии на правую чашку весов надо положить такой груз, сила тяжести которого равна этой силе, т.е. груз с массой Δm = ρV , где ρ - плотность воды, V - объем тела. А поскольку плотность тела по условию вчетверо больше плотности воды, то Δm = m/4.

(ответ - 1).
Для нахождения давления жидкости, в которой плавают те или иные тела, существует следующий прием. Если мысленно удалить тело из жидкости и заполнить освободившееся место той же жидкостью, то силы, действующие со стороны жидкости на стенки сосуда не изменяться. Действительно, на плавающее тело со стороны жидкости и со стороны тела на жидкость действует сила

ρgV_nч,

где ρ - плотность жидкости, V_{n ч} - объем погруженной в жидкость части тела.

Таким образом, тело действует на жидкость с той же силой, с которой на нее действовала бы жидкость, занимающая объем погруженной в воду части тела. Поэтому если вытащить тело из жидкости и заполнить освободившееся место жидкостью, то не меняется уровень жидкости, не меняются также все силы, действующие внутри жидкости.

Поэтому если в жидкости плавает тело, то независимо от параметров этого тела (массы, плотности, объема), давление жидкости на глубине h равно ρgh, причем h отсчитывается от поверхности жидкости с плавающим в ней телом.
18.) В задаче 5.8 надо найти, на сколько поднимется уровень воды в сосуде, а затем и связанное с этим повышением уровня избыточное гидростатическое давление около дна. Очевидно, что в цилиндрическом сосуде площадью сечения S уровень воды поднимется на такую величину Δh, что

ΔhS = V_n4,

где V_nч - объем погруженной в воду части тела. Находя величину V_пч из условия равновесия тела и закона Архимеда, получим Δh = m/ρS .

Поэтому гидростатическое давление воды около дна вырастет на величину

Δр = ρgΔh - mg/S.

(ответ - 1).

19). Задача 6.8. Из условия равновесия плавающего тела mg = pgV_nч следует, что его масса равна массе воды в объеме погруженной части тела m = ρF_nч. Поэтому суммарная масса воды и деревянного тела в одном ведре и суммарная масса воды и пенопластового тела в другом равна массе воды в полном ведре, т.е. одинакова в обоих ведрах.

(ответ – 3).

20). Задача 7.8. Когда внутрь плиты вставляют более плотное тело, возникает дополнительное гравитационное взаимодействие между жидкостью и плитой. Если до этого на каждый элемент жидкости действовала гравитационная сила, направленная вертикально вниз, то после этого возникает дополнительная сила, направленная к центру тела (см. рисунок, на котором нарисованы силы, действующие на выделенный элемент жидкости).

К каким последствиям для расположения жидкости на плите это приведет?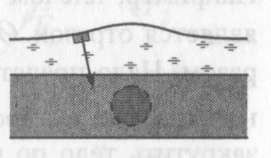





Легко сообразить, что уровень жидкости в области над телом повысится. Действительно, поверхность жидкости всегда расположена перпендикулярно приложенным силам (иначе жидкость будет течь), поэтому она расположится так, как показано на рисунке. Другими словами, более массивное тело, вставленное внутрь плиты, благодаря дополнительному гравитационному взаимодействию «натянет» жидкость со всех сторон, и ее уровень над телом поднимется. (ответ – 3).

9. Задания на проверку элементов знаний и умений по теме:

статика

(Задачи: 9.9; 10.9; 11.9; 12.9; 13.9; 14.9; 15.9; 16.9; 17.9; 18.9; 19.9; 20.9; 1.9; 2.9; 3.9; 4.9;5.9; 6.9; 7.9; 8.9.)

Статика - это раздел динамики, в котором рассматривается равновесие тел, и формулируются условия, при выполнении которых тела находятся в равновесии. Для успешного решения задач «на статику» необходимо уметь вычислять моменты сил, знать и уметь использовать условия равновесия тел. При этом следует помнить, что при вычислении моментов распределенных сил (тяжести, трения, реакции) возникает понятие центра тяжести тела, как точки, к которой надо приложить суммарную распределенную силу для вычисления ее момента.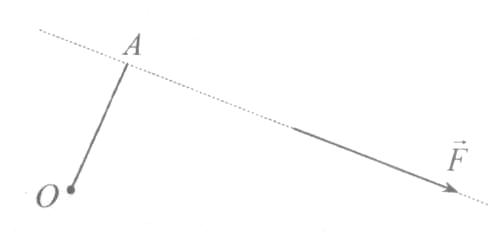

Момент силы определяется по отношению к некоторой точке, которую будем называть началом отсчета моментов, и которая выбирается произвольно. Моментом силы F называется произведение модуля силы на ее «плечо» d, которое определяется как длина перпендикуляра, опущенного из начала отсчета момента на прямую, вдоль которой действует сила

М = ± Fd.(10.1)

Например, плечом силы F относительно точки О (см. рисунок) является отрезок OA. Знак момента определяется следующим образом. Надо, представить, что через точку О проходит ось вращения тела, на которое действует сила F. Если сила F стремится закрутить тело по часовой стрелке относительно этой оси, то момент силы F отрицателен, если против часовой стрелки - положителен. (Следует иметь в виду, что знак момента можно было выбирать и наоборот.

Дело в том, что момент силы - это вектор. В школьном курсе, однако, определение вектора момент не вводится, и рассматриваются только такие ситуации, когда векторы момента направлены вдоль одной оси. Данное выше определение момента - это определение проекции вектора момента на эту ось. А поскольку направление оси никак не определяется, то важен только относительный знак проекций момента. Из определения момента (10.1) следует, что момент силы равняется нулю, если прямая, вдоль которой она действует, проходит через начало отсчета момента.

Если на неточечное тело действуют силы, у которых нет определенной точки приложения, например, сила тяжести, сила трения, сила реакции (такие силы принято называть распределенными), то для вычисления их моментов можно поступить следующим образом. Необходимо разбить это тело на бесконечно малые элементы, вы­числить момент силы, действующей на каждый элемент, просуммировать полученные моменты.

Оказывается, что если распределенные силы пропорциональны массам элементов и одинаково направлены, для вычисления момента распределенной силы нужно суммарную распределенную силу приложить к некоторой точке, которая называется центром тяжести тела.

Центр тяжести тела, обладающего центральной симметрией (а только такие тела и могут встретиться школьникам), находится в геометрическом центре тела.

Тело находится в равновесии по отношению к инерциальной системе отсчета, если сумма всех сил, действующих на тело, равна нулю

F₁+F₂+F₃+... = 0, (10.2)

и сумма моментов этих сил, вычисленных относительно произвольного начала отсчета, равна нулю

М₁ +М₂ +М₃ + ... = 0. (10.3)

Условия (10.2), (10.3) можно использовать для определения сил, действующих на тело, которое находится в равновесии.

Рассмотрим решение задач.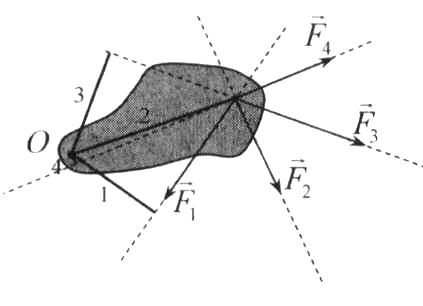

1). В задаче 9.9 начало отсчета моментов (точка О) лежит на линии действия силы F₃. Поэтому момент этой силы относительно точки О равен нулю.

(ответ - 3).

2). Задача 10.9. На рисунке числами 1, 2, 3 и 4 отмечены отрезки (толстые сплошные линии), которые представляют собой плечи сил F₂, F₃ или F₄ относительно точки О (линии действия сил показаны тонким пунктиром).

Из этого рисунка видим, что из этих сил наибольшее плечо имеет сила F₂.

(ответ - 2.).

3). Задача 11.9. Для момента первой силы имеем М = Fd.Тогда для момента второй силы получаем М₁ =F₁d₁ = nFkd = nkМ, т.е. момент второй силы в пk раз больше момента первой силы

(ответ - 1).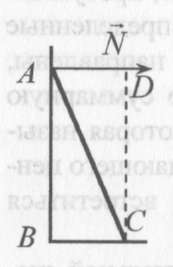

4). Задача 12.9. По определению плечо силы - это перпендикуляр, опущенный из начала отсчета момента (точки С) на линию действия силы.

Поэтому плечо силы реакции – отрезок CD (или АВ, который равен отрезку CD).

Следовательно, плечо силы реакции вертикальной стенки, действующей на лестницу, равно длине отрезка АВ.

(ответ - 1.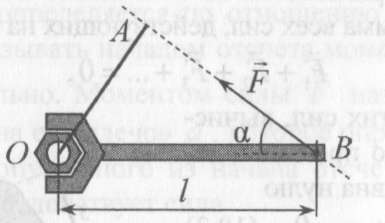

5). Задача 13.9. Плечо силы F равно отрезку OA (см. рисунок). Из прямоугольного треугольника ОАВ получаем для плеча силы

OA = lsinα.

Поэтому момент силы F равен

М = Flsinα = 5 Н·м

(ответ - 1).

6). Задача 14.9. На тело массой m, находящееся на наклонной плоскости с углом наклона α, со стороны плоскости действует сила реакции, направленная перпендикулярно плоскости и равная

N = mgcosα .

Поэтому момент этой силы относительно основания плоскости длиной l (см. рисунок в условии задачи) равен

mglcosα = 5 Н·м.

(ответ - 2).

7). Задача 15.9. Чтобы рычаг был в равновесии сумма моментов всех сил, действующих на рычаг, должна равняться нулю, причем относительно любой точки - начала отсчета моментов. На рычаг действуют: сила 3 Н на плечо длиной 0,1 м, искомая сила F - на плечо длиной 0,3 м и сила со стороны оси вращения.

Помещая начало отсчета моментов на оси вращения и находя моменты сил, действующих на плечи рычага, получаем из условия равновесия (10.3)

3 Н·0,1 м = F·0,3[м]

(момент силы, действующей на рычаг со стороны оси вращения равен нулю относительно выбранного начала).

Отсюда F = 1 Н