Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
 Скачать 1.57 Mb.
|
|
(ответ - 1). 8). Задача 16.9. Ось вращения стержня надо расположить в такой точке, чтобы сумма моментов сил F1 и F2 относительно этой оси равнялась бы нулю. При этом очевидно, что ось должна располагаться справа от точки приложения силы F2. Поскольку величина силы F2 втрое больше величины силы F1, то плечо силы F2 должно быть втрое меньше плеча силы F1. (ответ – 4) 9). Задача 17.9. Приравнивая величины моментов сил тяжести, действующих на тела, относительно опоры, получим mgx= 3mg(l - х), где х - расстояние от опоры до левого груза. Отсюда находим х = 31/4. (ответ - 2). 10). Задача 18.9. Аналогично получим F = 3mg/4. (ответ - 4). 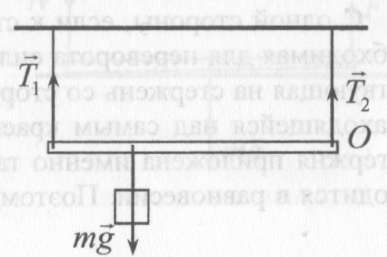 11). Задача 19.9. 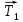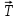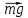На невесомый стержень действуют две силы натяжения нитей  и 2, и сила со стороны груза, равная его силе тяжести  (см. рисунок). Используем условие равновесия стержня (10.3). Моменты удобно вычислять относительно начала отсчета О, помещенного около правого конца стержня. Относительно этого начала имеем MT1 = -T1l,MF = (3/4)mgl, МT2 = 0 (здесь использовано, что точка крепления груза делит стержень в отношении 1:3). Поэтому из условия (10.3) получаем T1l = (3/4)mgl. Отсюда mg =4T1/3g = 4 кг. (ответ - 4). 12). Задача 20.9. Из условия равенства моментов, вращающих рычаг по и против часовой стрелки, получаем F·1 = mg·4 + 2mg·3 + 3mg·1 =13mg. (ответ - 4).  13). Задача 1.9. Как отмечалось во введении, для нахождения момента распределенной силы (в данном случае момента силы тяжести) нужно силу тяжести, действующую на весь стержень, «приложить» к геометрическому центру стержня (к его середине) (см. рисунок). Поэтому плечо силы тяжести относительно точки Оравно l/2 - l/4 = l/2 = 0,5 м (l- длина стержня), и момент силы тяжести относительно точки О равен М = mgl/ 4 = 2,5 Н. Здесь m - масса стержня. (ответ – 3). 14). Задача 9.9. Условие равновесия (10.3) относительно точки О дает Мmg + М Т = mgl/4 – (3/4)Tl = 0, где МT - момент силы натяжения относительно точки О. Отсюда находим Т = mg/3 (ответ - 3). 15). Задача 10.9. С одной стороны, если к стержню приложена минимальная необходимая для переворота сила, сила реакции, действующая на стержень со стороны стола, будет приложена к точке, находящейся над самым краем. С другой стороны, если к концу стержня приложена именно такая сила, стержень практически находится в равновесии. Поэтому в том случае, когда на тело действует минимальная необходимая для переворота сила, сумма моментов силы тяжести и искомой силы F относительно края стола равна нулю Fl/3 = mg(l/2 – l/3) = mgl/6. Отсюда находим F = mg/2 = 5 Н. (ответ - 2).  16). Задача 11.9. На стержень действуют сила тяжести m , реакции стенки  1 и пола 2, а также сила трения со стороны пола, направленная так, как показано на рисунке, причем сила тяжести приложена к середине стержня. Используем условие равенства нулю суммы моментов внешних сил (10.3) относительно нижней точки стержня. Поскольку моменты силы трения и силы реакции  относительно нижней точки стержня равны нулю, условие (10.3) дает(1/2)mglcosα = N1lsinα , где α - угол между стержнем и горизонтальной поверхностью (отмечен на рисунке дугой). Отсюда находим  15 Н.(ответ - 1).  17). Задача 12.9. При приложении к концу стержня минимально необходимой для отрыва этого конца от поверхности силы F одновременно выполнены два следующих условия. Поскольку стержень практически находится в равновесии, то еще выполнены уравнения статики - сумма моментов сил, действующих на стержень, равна нулю.С другой стороны, в этот момент стержень уже начинает отрываться от поверхности, и сила реакции опоры N будет приложена к другому концу стержня (см.рисунок). Поэтому сумма моментов силы F и силы тяжести относительно левого конца стержня должна равняться нулю mgl/2 - Fl = 0 . Отсюда F = mg/2. (ответ - 4). 18). Задача 13.9. При приложении к бруску минимально необходимой для его переворота силы F сумма моментов сил тяжести mg и F относительно упора (см. рисунок в условии) равна нулю. Этот вывод обосновывается так же, как и в предыдущей задаче. Поэтому F = mga/2h (ответ - 3).  19). В задаче 14.9 проще всего сравнить силы реакции упоров, из условия равенства нулю суммы всех сил, действующих на стержень (формула (10.2)). На стержень действуют три силы: тяжести m , и две силы реакции 1 и 2 (см.рисунок), сумма которых равна нулю, или mg + N2 = N1. Поэтому сила реакции нижнего упора N1 больше, чем верхнего N2. (ответ - 2).  20). Задача 15.9. Треугольник находится в равновесии, если его центр тяжести лежит на вертикальной прямой, проходящей через шарнир. Это связано с тем, что на треугольник действуют две силы - тяжести и реакции шарнира - и, чтобы выполнялось условие моментов относительно шарнира, момент силы тяжести относительно шарнира должен равняться нулю. Докажем, что центр тяжести треугольника лежит в точке пересечения его медиан. Действительно, если разбить треугольник на тонкие полоски, параллельные одной из сторон, то центр тяжести каждой из них лежит в ее середине. Поэтому и центры тяжести всех полосок (а, значит, и всего треугольника) лежат на его медиане (см. рисунок; медиана показана пунктиром). А поскольку треугольник можно разделить на слои, параллельные второй и третьей его стороне, то центр тяжести лежит и на этих медианах, т.е. в точке их пересечения. (ответ - 1) 10. Задания на проверку элементов знаний и умений по теме: механические колебания и волны (Задачи: 10.10; 11.10; 12.10; 13.10; 14.10; 15.10; 16.10; 17.10; 17.10; 18.10; 19.10; 20.10; 1.10; 2.10; 3.10; 4.10; 5.10; 6.10; 7.10; 8.10; 9.10.) Колебательным называется любое периодически повторяющееся во взаимообратных направлениях движение. Поэтому зависимости координаты х(t) и скорости тела v(t) от времени при колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются такие колебания, в которых зависимостиx (t) и скорости тела v(t) представляют собой тригонометрические функции cosωt, sinωt или их комбинацию, где ω - некоторое число. Такие колебания называются гармоническими (функции cosx и sinx часто называют гармоническими функциями). Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени x(t), которая в случае гармонических колебаний всегда может быть представлена в виде x(t) = Acos(ωt + φ) (11.1) где А, ω и φ - некоторые числа. Амплитудой колебаний называется максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значение косинуса в (11.1) равно ± 1, то амплитуда колебаний тела, совершающего колебания (11.1), равна величине А . Период колебаний - это минимальное время, через которое движение тела повторяется. Для зависимости (11.1) период можно установить из следующих соображений. Косинус - периодическая функция с периодом 2π. Поэтому движение полностью повторяется через такое значение Т, что ω(t + Т) + φ = ωt + φ + 2π. Отсюда получаем  (11.2)Частотой колебаний тела называется число колебаний, совершаемых в единицу времени. Очевидно, что частота колебаний ν связана с периодом колебаний по формуле  (11.3)Круговой (или циклической) частотой колебаний называется число колебаний, совершаемых за 2π единиц времени. Из формулы (11.3) заключаем, что круговой частотой является величина ω из формулы (11.1). Фазой колебаний называется аргумент тригонометрической функции, описывающей зависимость координаты от времени. Из формулы (11.1) видим, что фаза колебаний тела, движение которого описывается зависимостью (11.1), равна ωt + φ. Значение фазы колебаний в момент времени t = 0 называется начальной фазой. Для зависимости (11.1) начальная фаза колебаний равна величине φ. Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента t = 0 ), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот. В программу единого государственного экзамена входит также знание формул для частоты колебаний пружинного и математического маятников. Пружинным маятником принято называть тело, которое может совершать колебания на гладкой горизонтальной поверхности под действием пружины, второй конец которой закреплен. Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити. Название этой системы - «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника  , (11.4)где k -коэффициент жесткости пружины, т - масса груза Период колебаний математического маятника определяется следующим соотношением  (11.5)где l - длина нити, g - ускорение свободного падения. Волна - некоторый колебательный процесс, который может распространяться в среде. При этом каждая точка среды совершает колебания около определенного положения и в среднем не перемещается в пространстве. Волна характеризуется периодом Т (или связаннойc ним частотой ν = 1/T), скоростью с и длиной волны λ, которая определяется как минимальное расстояние между точками, колеблющимися в одинаковой фазе. Для решения задач ЕГЭ по этой теме необходимо помнить формулу, дающую связь между параметрами волны λ = cT = c/ν, (11.6) которую легко запомнить, поскольку эта связь имеет такой же вид как обычное соотношение между расстоянием, скоростью и временем. Рассмотрим применение этих определений и законов на примере решения задач. 1). Задача 10.10. Чтобы найти циклическую частоту колебаний груза найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 мин и 28 с - это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1с-1 (ответ- 2). 2). В задаче 11.10 груз за 600 с совершил 60 колебаний, поэтому частота колебаний - 0,1 с -1 (ответ - 1). 3). Задача 12.10. Чтобы понять, какой путь пройдет груз за 2,5 периода, проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия - одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону - вторая, назад в положение равновесия - третья, из положения равновесия в начальную точку - четвертая. За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода - две амплитуды. Поэтому пройденный путь равен десяти амплитудам. (ответ- 4). 4). Задача 13.10. Величина перемещения тела - расстояние от начальной точки до конечной. За 2,5 периода тело успеет совершить два полных и половину полного колебания, т.е. окажется на максимальном отклонении, но с другой стороны от положения равновесия. Поэтому величина перемещения равна двум амплитудам. (ответ - 3). 5). Задача 14.10. По определению фаза колебаний - это аргумент тригонометрической функции, которой описывается зависимость координаты колеблющегося тела от времени. (ответ – 3). 6). Задача 15.10. Период - это время полного колебания. Это значит, что возвращение тела назад в ту же точку, из которой тело начало движение, еще не означает, что прошел период: тело должно вернуться в ту же точку с той же скоростью. Например, тело, начав колебания из положения равновесия, за период успеет отклониться на максимальную величину в одну сторону, вернуться назад, отклонится на максимум в другую сторону и снова вернуться назад. Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения тело затрачивает четвертую часть периода. (ответ - 3). 7).Задача 16.10. Гармоническими называются такие колебания, при которых зависимость координаты колеблющегося тела от времени описывается тригонометрической (синус или косинус) функцией времени. Таковыми являются функции x1и x3, несмотря на то, что входящие в них параметры обозначены как А2 и ω2. Функция же х2 - тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин х1 и х2. (ответ - 4). 8). Задача 17.10. При гармонических колебаниях скорость тела изменяется по закону v(t) = v0sinωt, где v0- амплитуда колебаний скорости (начало отсчета времени выбрано так, чтобы начальная фаза колебаний равнялась бы нулю). Отсюда находим зависимость кинетической энергии тела от времени  Используя далее известную тригонометрическую формулу, получаем  Из этой формулы следует, что кинетическая энергия тела изменяется при гармонических колебаниях также по гармоническому закону, но с удвоенной частотой. (ответ - 2). 9). Задача 18.10. За соотношением между кинетической энергий груза и потенциальной энергией пружины легко проследить из следующих соображений. Когда тело отклонено на максимальную величину от положения равновесия, скорость тела равна нулю, и, следовательно, потенциальная энергия пружины больше кинетической энергии груза. Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза. (ответ - 2). 10). Задача 19.10. Амплитуду колебаний скорости проще всего найти по закону сохранения энергии. В точке максимального отклонения энергия колебательной системы равна потенциальной энергии пружины kА2/2, где k - коэффициент жесткости пружины, А - амплитуда колебаний. При прохождении положения равновесия энергия тела равна кинетической энергии m  / 2,где m - масса тела, v0 - скорость тела при прохождении положения равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебаний скорости. Приравнивая эти энергии, находим:  где использовано выражение для круговой частоты колебаний груза на пружине:  . (ответ - 1)11). Задача 20.10. По формуле (11.4) получаем  (ответ - 4). 12). Задача 1.10. Из формулы(11.5) заключаем, что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ - 1). 13). Задача 2.10. Часы - это колебательный процесс, который используется для измерения интервалов времени. Слова часы «спешат» означают, что период этого процесса меньше того, каким он должен быть. Поэтому для уточнения хода этих часов необходимо увеличить период процесса. Согласно формуле (11.5) для увеличения периода колебаний математического маятника необходимо увеличить его длину. (ответ - 3). 14). Задача 3.10. Чтобы найти амплитуду колебаний, необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции x(t) = Acosωt + Вsinωt это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на  и используя формулу сложения тригонометрических функций, получим: где φ - такой угол, что tgφ = А/В. Из этой формулы следует, что амплитуда колебаний тела .(ответ 4). 15). В задаче 4.10 имеем при ωt = π/6: Asin (π/6) = 10 см. Откуда А = 10 см (ответ 2). 16). Задача 5.10. По формуле (11.6) находим длину волны λ. = с/ν = 6/3 = 2 м (ответ - 2). 17). Задача 6.10. Как следует из рисунка длина волны, распространяющейся по шнуру, равна λ. = 0,5 м. Поэтому по формуле (11.6) имеем v=c/λ = 2/0,5 = 4 Гц (ответ 4). 18). Задача 7.10. Поскольку в момент максимального отклонения пружинного маятника, механическая энергия системы равна потенциальной энергии пружины, то  ,где А - амплитуда колебаний, k - жесткость пружины. Поэтому при увеличении механической энергии пружинного маятника в 2 раза амплитуда колебаний увеличилась в  раз.(ответ - 1). 19). Задача 8.10. Используя известную тригонометрическую формулу, получим x(t) =Acos2ωt = (A/2) (1 - cos 2ωt) = (A/2) – (A/2)cos2ωt. Эта зависимость представляет собой гармоническую функцию, но колеблющуюся вокруг точки х = А/2. Амплитудой этих колебаний является множитель перед косинусом - А/2(так как сам косинус меняется в интервале от -1 до 1). Циклической частотой - величина 2ω. (ответ 4). 20). Задача 9.10. Вертикальный пружинный маятник отличается от горизонтального наличием силы тяжести. Однако сила тяжести приводит только к сдвигу положения равновесия маятника, а возвращающая сила по прежнему будет зависеть от смещения маятника Δх от положения равновесия по закону Fx = k·Δх (так как возвращающей силой будет разность силы упругости и постоянной силы тяжести). Поэтому период колебаний груза на вертикальной и горизонтальной пружине - одинаков (конечно, при условии, что и сам груз и пружины одинаковы). (ответ – 3). |