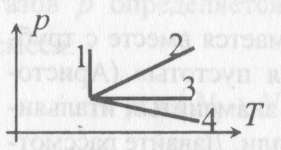|
|
Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
(ответ - 2)
20). Задача 1.2. Сначала обратим внимание читателя, что предложенные в задаче значения температур и варианты ответов «подталкивают» к выбору ответа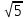 , поскольку конечная температура в 5 раз больше начальной. , поскольку конечная температура в 5 раз больше начальной.
Тем не менее, это неправильно, поскольку температуры заданы в градусах Цельсия, а в формулу (12.2), связывающую температуру и среднюю кинетическую энергию молекул, входит абсолютная температура. Поэтому
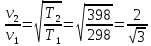 . .
(ответ- 4).
2. Задания на проверку элементов знаний и умений по теме:
газовые законы.
(Задачи:3.3; 4.3; 5.3; 6.3; 7.3; 8.3; 9.3; 10.3; 1.3; 2.3; 4.4; 5.4; 6.4; 7.4; 8.4; 9.4; 10.4; 1.4; 2.4; 3.4.)
Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона- Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях.
Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
р = пкТ, (13.1)
где р - давление газа, n - концентрация молекул газа (число молекул в единице объема), k - постоянная Больцмана, Т - абсолютная (в шкале Кельвина) температура. Учитывая, что п =N/V , где N - число молекул газа, V - объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)
pV = NkT. (13.2)
Число молекул N можно связать с количеством вещества газа :
N = νNa,
где Na - число Авогадро. Поэтому формулу (13.2) можно переписать в виде
pV = νNAkT = νRT , (13.2)
где произведение постоянных Авогадро и Больцмана обозначено как R = NAk . Постоянная R = 8,31 Дж/(К - моль) называется универсальной газовой постоянной.
Количество вещества газа можно также выразить через его массу m и молярную массу этого газа µ
ν = m/µ (13.3)
С учетом (13.3) закон (13.2) можно переписать и в таком виде
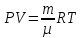 (13.4) (13.4)
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона - Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется.
В изобарическом процессе не изменяется давление газа,
в изотермическом - температура,
в изохорическом - объем.
Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса

Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
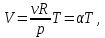 (13.5) (13.5)
где α - постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
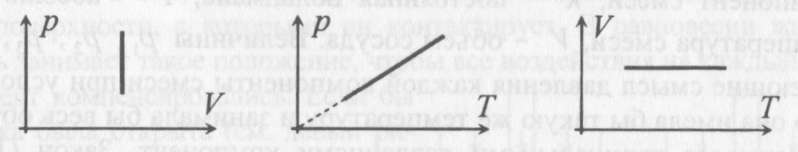
Второй график следует из соотношения
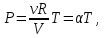 (13.6) (13.6)
где α–постоянная при постоянном объеме.
Для изотермического процесса

Первый график следует из закона Клапейрона - Менделеева, который при постоянной температуре газа можно привести к виду
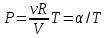 (13.7) (13.7)
где α - постоянная. Отсюда следует, что графиком зависимости ротV в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах - единственный параметр собственно газа, входящий в уравнение состояния, - это число молекул.
Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление.
Отсюда следует, что и давление смеси идеальных газов р определяется суммарным числом молекул всех компонент смеси:
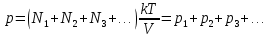 (13.8) (13.8)
где N1, N2, N3 ... - число молекул первой, второй, третьей и т.д. компонент смеси, k - постоянная Больцмана, Т - абсолютная температура смеси, V - объем сосуда. Величины р1, р2, р3, ... ,имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона.
Рассмотрим теперь в рамках этих законов предложенные задачи.
1). В задаче 3.3 из уравнения состояния в форме(13.1), получаем для давления в конце процесса:
р1 =(2п)k(3Т) = 6пkТ = 6р,
т.е. давление газа увеличилось в 6 раз.
(ответ_-_1).'>(ответ - 1).
2). Задача 4.3. Применяя закон Клапейрона - Менделеева (13.2) к первому и второму газам, получаем
p0V0=1·RT0, (2p0)V = 2·R(2T0),
где V - искомый объем. Сравнивая первую и вторую формулы, заключаем, что
V = 2V0
(ответ - 1).
3). Задача 5.3. Закон Клапейрона - Менделеева для газа в начальном и конечном состояниях дает
pV = 2RT, (3p)V = 3RTx,
где Тх - неизвестная температура. Из сравнения этих формул получаем
Тх = 2Т,
т.е. температуру газа в сосуде нужно повысить вдвое.
(ответ- 2).
4). Задача 6.3. Из закона Клапейрона - Менделеева для начального и конечного состояний газа имеем
pV = vRT,(2p)V = ν1R(2,5T).
Отсюда ν1 = 1,25ν, т.е. количество вещества газа в сосуде увеличилось в 1,25 раза.
(ответ - 3).
5). Задача 7.3. Первым, кто понял, почему жидкость поднимается вместе с трубкой, и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли.
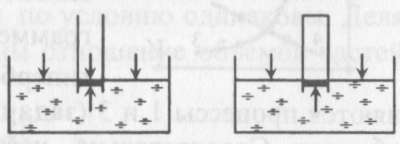 Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке.
Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу.
Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней.
Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости - атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, - 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля.
(ответ- 4).
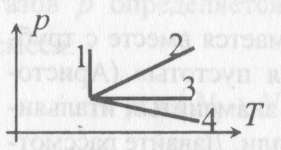 6). Задача 8.3. Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 - изотермический, 2 - изохорический, 3 - изобарический. 6). Задача 8.3. Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 - изотермический, 2 - изохорический, 3 - изобарический.
В процесс 4 меняются и давление, и объем, и температура газа.
(ответ - 4).
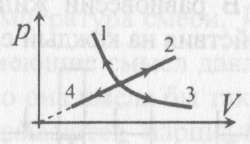 7). Задача 9.3. В изотермическом процессе давление зависит от объема как р 7). Задача 9.3. В изотермическом процессе давление зависит от объема как р 1/V; на диаграмме p - V этот процесс изображается гиперболой. Поэтому изотермическими являются процессы 1 и 3, но в процессе 1 объем газа убывает. Следовательно, изотермическим расширением является процесс 3.
(ответ - 3).
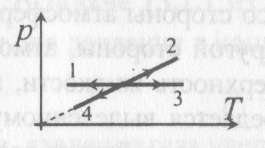 8). Задача 10.3. Изохорическим охлаждением является процесс 4 (см. рисунок) 8). Задача 10.3. Изохорическим охлаждением является процесс 4 (см. рисунок)
|
|
|
 Скачать 1.57 Mb.
Скачать 1.57 Mb. 8). Задача 10.3. Изохорическим охлаждением является процесс 4 (см. рисунок)
8). Задача 10.3. Изохорическим охлаждением является процесс 4 (см. рисунок)
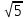 , поскольку конечная температура в 5 раз больше начальной.
, поскольку конечная температура в 5 раз больше начальной. 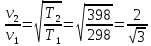 .
.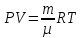

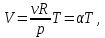 (13.5)
(13.5)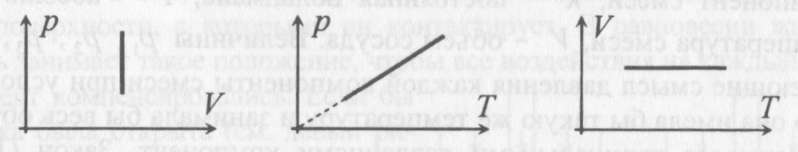
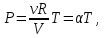 (13.6)
(13.6)
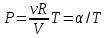 (13.7)
(13.7)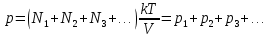 (13.8)
(13.8)