Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
 Скачать 1.57 Mb.
|
|
В задаче 7.7 необходимо использовать то обстоятельство, что работа газа в циклическом процессе численно равна площади цикла на графике зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» - если против. Поэтому во втором цикле работа газа положительна, в третьем отрицательна. Первый цикл состоит из двух циклов, один из которых проходится по, второй - против часовой стрелки, причем, как следует из графика 1, площади этих циклов равны. Поэтому работа газа за цикл в процессе 1 равна нулю (ответ - 2). 2). Задача 8.7. Поскольку в результате совершения циклического процесса газ возвращается в первоначальное состояние, то изменение внутренней энергии газа равно нулю (ответ - 2). 3). Задача 9.7. Применяя первый закон термодинамики ко всему циклическому процессу и учитывая, что изменение внутренней энергии газа равно нулю (см. предыдущую задачу), заключаем, что A = Q. (ответ - 3). 4).Задача 10.7. Поскольку работа газа численно равна площади цикла на диаграмме «давление-объем», то работа газа в процессе равна A = pV/2. (ответ - 1). 5). Задача 1.7. Аналогично в этой задаче газ за цикл совершает работу А = 2pV. (ответ - 1). 6). Задача 2.7. Работа газа в любом процессе равна сумме работ на отдельных участках процесса. Поскольку процесс 2-3 изохорический, то работа газа в этом процессе равна нулю. Поэтому А = А1-2 + А3-1. (ответ - 3). 7). Задача 3.7. По определению КПД показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу. (ответ - 4). 8). Задача 4.7. Работа двигателя за цикл равна разности количеств теплоты, полученного от нагревателя Q1 и отданного холодильнику Q2: А = Q1 - Q2. Поэтому КПД цикла есть 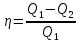 .(ответ - 3). 9). Задача 5.7. По формуле (15.3) находим КПД цикла Карно 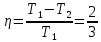 .(ответ - 2). 10). Задача 6.7. Пусть температура нагревателя первоначального цикла Карно равна T1, температура холодильника Т2. Тогда по формуле (15.3) для КПД первоначального цикла имеем 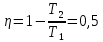 Отсюда находим T2/T1 = 0,5 . Поэтому для КПД нового цикла Карно получаем 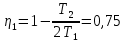 .(ответ - 2). 11). В задаче 8.8 формулы (2),(3) и(4) представляют собой разные варианты записи определения КПД теплового двигателя (см. формулы (15.1) и (15.2)). Поэтому не определяет КПД двигателя только формула 1. (ответ - 1). 12). Задача 9.8. Мощностью двигателя называется работа, совершенная двигателем в единицу времени. Поскольку работа двигателя равна разности полученного от нагревателя и отданного холодильнику количеств теплоты, имеем для мощности двигателя N  = 700 Вт.(ответ - 3). 13). Задача 10.8. По формуле (15.2) имеем для КПД двигателя  .(ответ - 2). 14). Задача 1.8. Для нахождения КПД теплового двигателя удобно использовать последнюю из формул (15.2). Имеем  где А - работа газа, Qx - количество теплоты, отданное холодильнику. (ответ - 3). 15). Задача 2.8. Пусть газ совершает за цикл работу А. Поскольку количество теплоты, полученное от нагревателя равно A + Qx (Qx - количество теплоты, отданное холодильнику), и работа А составляет 20 % от этой величины, то для работы справедливо соотношение А = 0,2(А + 100). Отсюда находим А = 25 Дж. (ответ - 1). 16). Задача 3.8. Поскольку работа теплового двигателя равна 100 Дж при КПД двигателя 25 %, то двигатель получает от нагревателя количество теплоты 400 Дж. Поэтому он отдает холодильнику 300 Дж теплоты в течение цикла. (ответ- 4).  17). В задаче 4.8 газ получает или отдает теплоту только в процессах 1-2 и 3-1 (процесс 2-3 по условию адиабатический). Поэтому данное в условии задачи количество теплоты Q1-2 является количеством теплоты, полученным от нагревателя в течение цикла, Q3-1, - количеством теплоты, отданном холодильнику. Поэтому работа газа равна А = Q1-2- Q3-1. (ответ - 1). 18). Задача 5.8. Цикл состоит из двух изотерм 2-3 и 4-1 и двух изохор 1-2 и 3-4.  Работа газа в изохорических процессах равна нулю. Сравним работы газа в изотермических процессах. Для этого удобно построить график зависимости давления от объема в рассматриваемом процессе, поскольку работа газа есть площадь под этим графиком. График зависимости давления от объема для заданного в условии процесса приведен на рисунке. Поскольку изотерме 2-3 соответствует большая температура, чем изотерме 4-1, то она будет расположена выше на графике p- V. Объем газа в процессе 2-3 увеличивается, в процессе 4-1 уменьшается. Таким образом, график процесса на графике p-V проходится по часовой стрелке, и, следовательно, работа газа за цикл положительна. (ответ - 1).  19). Задача 6.8. Для сравнения работ газа на различных участках процесса построим график зависимости давления от объема. Этот график представлен на рисунке. Из рисунка следует, что работы газа в процессах 1-2 и 3-4 одинаковы по модулю (этим работам отвечают площади прямоугольников, «залитых» на рисунке светлой и темной «заливкой»). Работе газа на участке 4-1 отвечает площадь под графиком 4-1, которая меньше площади под графиком 1-2. Работе газа на участке 2-3 отвечает площадь под кривой 2-3 на рисунке, которая заведомо больше площади «залитых» прямоугольников. Поэтому в процессе 2-3 газ и совершает наибольшую по абсолютной величине (среди рассматриваемых процессов) работу. (ответ - 2.). 20). Задача 7.8. Согласно определению коэффициент полезного действия представляет отношение работы газа за цикл А к количеству теплоты Q, полученному от нагревателя 𝛈 = А/Q. Как следует из данного в условии задачи графика, и в процессе 1-2-4-1 и в процессе 1-2-3-1 газ получает теплоту только на участке 1-2. Поэтому количество теплоты, полученное газом от нагревателя в процессах 1-2-4-1 и 1-2-3-1 одинаково. А вот работа газа в процессе 1-2-4-1 вдвое меньше (так площадь треугольника 1-2-4 как вдвое меньше площади треугольника 1-2-4-1). Поэтому коэффициент полезного действия процесса 1-2-4-1 - 𝛈1вдвое меньше коэффициента полезного действия процесса 1-2-3-1 - 𝛈.  (ответ - 1). 5. Задания на проверку элементов знаний и умений по теме: свойства газов, жидкостей и твердых тел. Фазовые переходы. Влажность (Задачи: 9.9; 10.9; 1.9; 2.9; 3.9; 4.9; 5.9; 6.9; 7.9; 8.9; 10.10; 1.10; 2.10; 3.10; 4.10; 5.10; 6.10; 7.10; 8.10; 9.10.) Задачи и вопросы, в которых рассматриваются свойства газов, жидкостей и твердых тел, а также переходы между ними (фазовые переходы), входят в программу школьного курса физики и часто включаются в ЕГЭ. Начнем со свойств трех агрегатных состояний вещества. Плотности жидкостей и твердых тел близки друг к другу, но сильно отличаются от плотности газа. Отсюда следует, что расстояния между молекулами в жидкости и твердом теле не сильно отличаются друг от друга, но гораздо меньше расстояния между молекулами в газе. Различие же молекулярного строения жидкостей и твердых тел заключается в том, что большинство твердых тел имеют кристаллическую структуру: их молекулы располагаются в определенном порядке, повторяя определенную структурную единицу, которая называется элементарной ячейкой. Различают моно- и поликристаллы. Монокристаллом называется такое кристаллическое тело, порядок в расположении молекул которого имеет место вдоль всего тела. Очень часто монокристаллическое тело обладает правильной геометрической формой. Поликристалл представляет собой совокупность связанных друг с другом, хаотически ориентированных по отношению друг к другу маленьких монокристаллов. Из-за того, что разные направления в элементарной ячейке кристалла неэквивалентны, ряд его физических свойств, таких как прочность, электро - или теплопроводность неодинаковы в различных направлениях. Это свойство кристалла называется анизотропией. Конечно, это касается только монокристалла. Поликристаллы из-за различных ориентаций монокристаллических частей являются изотропными. Также изотропными являются жидкости, молекулы которых расположены беспорядочно. Существуют, однако, такие тела, которые являются твердыми, но в расположении молекул, которых нет кристаллического порядка. Такие тела называются аморфными. Аморфными являются биополимеры, стекло и ряд других веществ. Отсутствие порядка в расположении молекул проявляется в отсутствие у аморфных тел строго определенной температуры плавления (см. ниже). Как показывает опыт, при изменении температуры и внешнего давления возможны переходы вещества из одного агрегатного состояния в другое. Переход кристаллического твердого тела в жидкое называется плавлением, обратный процесс - кристаллизацией. Переход жидкости в пар называется испарением (или кипением, если этот процесс сопровождается образованием пузырьков пара в жидкости), обратный процесс - конденсацией. Плавление и кристаллизация твердых (кристаллических) тел происходит при строго определенной для каждого вещества (при фиксированном давлении) температуре. При плавлении необходимо сообщить твердому телу энергию, которая расходуется не на нагревание тела, а на разрыв кристаллических связей между его молекулами. При кристаллизации эта дополнительная энергия выделяется. Плавление аморфных тел происходит по-другому: при увеличении температуры они плавятся постепенно (т.е. становятся более мягкими и пластичными), и невозможно указать такую температуру, ниже которой тело твердое, выше - жидкое. При испарении жидкостей молекулы вылетают с их поверхности и переходят в газовую фазу. При этом из жидкости могут вылететь только самые быстрые молекулы, поэтому температура жидкости в процессе испарения понижается. Испарение может происходить при любой температуре (за исключением абсолютного нуля), однако с ростом температуры интенсивность испарения возрастает. Благодаря хаотическому тепловому движению наряду с процессом испарения идет и обратный процесс - конденсация пара, - в результате которого молекулы пара могут вернуться в жидкость. Поскольку скорость процесса конденсации зависит от плотности пара над поверхностью жидкости, при определенной концентрации пара скорости процессов испарения и конденсации совпадают. В этом состоянии не происходит изменения количества жидкости и пара, и устанавливается динамическое равновесие между жидкостью и паром. Пар, находящийся в динамическом равновесии со своей жидкостью называется насыщенным. Насыщенный пар - это пар максимально возможной плотности (при фиксированной температуре). Действительно, если плотность пара станет больше плотности насыщенного пара, то скорость процесса конденсации станет больше скорости испарения - излишек пара сконденсируется, а оставшийся пар станет насыщенным. Пар, имеющий плотность, меньшую плотности насыщенного пара при данной температуре, называется ненасыщенным. Поскольку скорость процесса испарения зависит от температуры жидкости, динамическое равновесие между жидкостью и ее паром при большей температуре установится при больших концентрациях пара. Это значит, что концентрация насыщенного пара возрастает с температурой, и, следовательно, его давление растет с ростом температуры быстрее, чем по линейному закону. Характеристикой воздуха, в котором находятся водяные пары, является его относительная влажность φ, которая показывает какую долю парциальное давление данного пара р (или его концентрация) составляет от давления (или концентрации) насыщенного пара при данной температуре рнас:  (16.1)Если, например, парциальное давление водяного пара в воздухе при некоторой температуре равно 103 Па, а давление насыщенного пара при этой температуре равно 2·103 Па, то относительная влажность этого воздуха составляет 50 %. Очевидно, изменяя температуру и объем воздуха можно менять его относительную влажность. Поскольку концентрация насыщенного пара зависит от температуры, при нагревании воздуха, в котором находится неизменное количество водяных паров, будет убывать его относительная влажность, при охлаждении - возрастать. Если в последнем процессе относительная влажность достигает 100 %, излишек пара конденсируется и при дальнейшем охлаждении относительная влажность не изменяется. Процесс конденсации излишка пара при охлаждении можно наблюдать прохладными ночами летом, когда выпадает роса и образуется туман (маленькие капельки воды). Т Температура, при которой пар становится насыщенным и образуется конденсат, называется точкой росы этого пара. Также можно изменять относительную влажность воздуха, уменьшая или увеличивая его объем при неизменной температуре. В первом процессе растет концентрация пара (и, следовательно, его относительная влажность), во втором убывает. Конечно, в этих рассуждениях предполагается, что масса водяного пара не изменяется (т.е. не происходит дополнительного испарения воды или конденсации пара). Процесс испарения жидкости с образованием пузырьков внутри нее называется кипением. Причина кипения заключается в следующем. Благодаря хаотическому тепловому движению в жидкости всегда образуются микроскопические пузырьки пара. Поскольку они очень малы, пар в них мгновенно становится насыщенным. Дальнейшая «судьба» этих пузырьков зависит от соотношения давлений: внутреннего, которое равно давлению насыщенного пара при данной температуре, и внешнего, которое равно давлению атмосферного воздуха (в пренебрежении гидростатическим давлением жидкости). Если внутреннее давление меньше внутреннего, пузырек пара пропадет, а пар из него перейдет в жидкость, если наоборот - пузырек будет расширяться, при этом за счет интенсивного испарения жидкости с поверхности пузырька, пар в нем будет оставаться насыщенным. Затем такие пузырьки всплывают, и пар из них уходит из жидкости. Таким образом, кипение жидкости происходит при такой температуре, при которой давление насыщенного пара этой жидкости равно атмосферному давлению. 1). |