Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
 Скачать 1.57 Mb.
|
|
изохоричеcком процессе не совершается работа, поэтому Q = ΔU. (14.7) В изотермическом процессе не меняется внутренняя энергия газа, поэтому Q = A. (14.8) В адиабатическом процессе (процессе без теплообмена с окружающей средой) Q = 0, поэтому 0 = ΔU + A. (14.9) В изобарическом процессе есть связь между изменением внутренней энергии газа и его работой. Из формул (14.1) и (14.5) заключаем, что работа одноатомного идеального газа и изменение его внутренней энергии в изобарическом процессе связаны соотношением 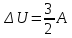 (14.10)Для характеристики процессов нагрева-остывания тела вводят понятие теплоемкости тела С, которая определяется как 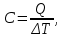 (14.11)где Q - количество теплоты, сообщенное телу в некотором процессе, ΔT - изменение его температуры в этом процессе. Подчеркнем, что Q и ΔT в формуле (14.11) не независимы, а связаны друг с другом: ΔT - это то изменение температуры, которое происходит благодаря сообщению телу количества теплоты Q. Поэтому теплоемкость (14.11) не зависит от Q и ΔT, а зависит от свойств тела и происходящего с ним процесса. Если тело однородно, то его теплоемкость пропорциональна его массе т . Поэтому отношение С/т = с является характеристикой вещества тела и называется его удельной теплоемкостью. Удельная теплоемкость представляет собой экспериментально измеряемую (табличную) характеристику веществ. Из определения удельной теплоемкости следует, что если телу массой m , изготовленному из вещества с удельной теплоемкостью с, сообщить количество теплоты Q, то будет справедливо соотношение cmΔT = Q (14.12) где ΔT - изменение температуры тела. Приведем теперь решения данных в первой части задач. 1). В задаче 5.5 внутренняя энергии газа увеличится согласно формуле (14.1). (ответ – 1). 2). Задача 6.5. Для ответа на вопрос удобно использовать формулу для внутренней энергии газа в виде (14.2). По этой формуле находим, что внутренняя энергия увеличилась в 3 / 2 раза Обратим внимание читателя, что причина изменения давления и объема может быть любой - ответ от этого не зависит. Может измениться или температура газа, или количество вещества, или и то и другое одновременно. (ответ - 2). 3) Задача 7.5. Поскольку температура и количество вещества газа не изменялись в рассматриваемом в задаче процессе, внутренняя энергия газа не изменилась. (ответ - 3). 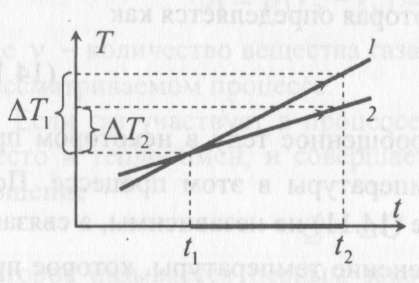 4). В задаче 8.5 следует воспользоваться определением теплоемкости (14.11). Для этого рассмотрим, например, интервал времени t1 - t2, выделенный жирным на оси времени (см. рисунок). За этот интервал оба тела получили одинаковое количество теплоты Q, поскольку нагреватели одинаковы.Изменение температур тел ΔТ1 и ΔТ2 можно определить по графику - эти величины отмечены фигурными скобками на оси температур. Поскольку ΔT1 > ΔТ2 из формулы (14.11) заключаем, что С1 < С2. (ответ – 2). 5). В задаче 9.5 следует воспользоваться определением удельной теплоемкости. По формуле (14.12) находим 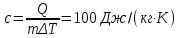 (ответ - 1). 6). Задача 10.5. Для совершения работы необходимо механическое движение. Поскольку объем газа не меняется, механическое движение отсутствует, работа газа равна нулю. (ответ- 4). 7). Задача 1.5. Применяя к рассматриваемому в задаче процессу первый закон термодинамики Q = ΔU + А (14.6) и учитывая, что в изохорическом процессе работа газа равна нулю, заключаем, что ΔU = Q. (ответ - 3). 8). Задача 2.5. В изотермическом процессе не меняется внутренняя энергия идеального газа. Поэтому ΔU = 0, и работа А, совершенная над газом, определяется соотношением (14.4), (14.6):A = -Q. (ответ - 2). 9). Задача 3.5. Адиабатический процесс происходит без теплообмена с окружающими телами: Q = 0. Поэтому из первого закона термодинамики (14.6) получаем для работы газа А = ΔU (ответ - 2). 10). Задача 4.5. Применяя первый закон термодинамики (14.6) к процессу, происходящему с газом найдем, что внутренняя энергия газа увеличилась на 10 Дж. (ответ - 2). 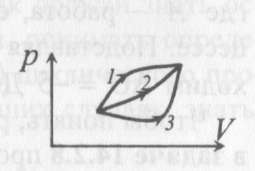 11). Задача 6.6. Для решения задачи можно использовать то обстоятельство, что работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объема и осью объемов. Из рисунка следует, что наибольшей является площадь под графиком процесса 1. Поэтому большую работу газ совершает в процессе 1.(ответ - 1). 12). В задаче 7.6. следует применить ко всем трем процессам, графики которых даны на рисунке к решению предыдущей задачи, первый закон термодинамики (14.6) Q = ΔU + А Учитывая, что начальная и конечная температура газа во всех трех процессах одинакова, и, следовательно, одинаковы изменения внутренней энергии газа ΔU, а работа наибольшая в процессе 1 (см. решение предыдущей задачи), заключаем, что газ получил большее количество теплоты в процессе 1. (ответ - 1). 13). Задача 8.6. Работа газа положительна, если газ расширяется. Для доказательства этого утверждения представим газ в сосуде, ограниченном подвижным поршнем. Если газ расширяется, то и перемещение поршня и сила, действующая на него со стороны газа, направлены одинаково, поэтому работа газа положительна. При сжатии газа его работа отрицательна. Поэтому работа газа положительна в процессе 3. (ответ - 3). 14). Задача 9.6. Так как графики процессов 1-2 и 3-4 прямые, проходящие через начало координат, эти процессы - изохорические, и газ не совершает в них работу. А поскольку изменение внутренней энергии газа в этих процессах одинаково, то одинаковы и количества теплоты, сообщенные газу в этих процессах. (ответ - 3). 15). Задача 10.6 аналогична предыдущей. Рассматриваемый процесс – изохорический и изменение внутренней энергии газа равно сообщенному количеству теплоты ΔU = 100 кДж. (ответ - 2). 16). Задача 1.6. Вычисляя площадь под графиком процесса, находим работу газа А = 2p0V0 (ответ - 2). 17). Задача 2.6. В условии дано количество теплоты Q, которое забрали у газа. Первый закон термодинамики, в который входит эта величина, имеет вид ΔU = A-Q, где А - работа, совершенная над газом в рассматриваемом процессе. Подставляя в эту формулу данные в условии величины, находим ΔU = -5 Дж. (ответ - 1). 18). Задача 3.6. Чтобы понять, расширялся или сжимался газ в рассматриваемом в задаче процессе, из первого закона термодинамики найдем работу газа: если она окажется положительной, газ расширялся, если отрицательной - сжимался. Из закона (14.6) находим A = Q-ΔU = Q – (3/2)vRΔT = 2·103 - 2,5·103 < 0.Поэтому газ сжимался. (ответ - 1). 19). Задача 4.6. Чтобы найти долю количества теплоты, которая пошла на увеличение внутренне энергии газа в изобарическом процессе) воспользуемся формулой (14.5) для работы газа в этом процессе А = vRΔT . Поскольку изменение внутренней энергии одноатомного идеального газа равно ΔU = (3/2)vRΔT, заключаем, что изменение внутренней энергии газа составляет 3/2 от его работы. Поэтому 2/5количества теплоты, сообщенного газу в изобарическом процессе тратится на работу, 3/5 - на изменение внутренней энергии газа (ответ - 3). 20). Задача 5.6. Чтобы найти теплоемкость газа в изотермическом процессе, применим к этому процессу определение теплоемкости (14.11) 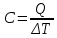 Поскольку в изотермическом процессе ΔТ = 0 при ненулевом количестве сообщенной теплоты, то теплоемкость газа равна бесконечности. Это означает следующее - в изотермическом процессе газу сообщают теплоту, а он не нагревается, что и означает бесконечную теплоемкость газа (теплота расходуется только на совершение работы). (ответ – 2). 4. Задания на проверку элементов знаний и умений по теме: работа газа в циклическом процессе. Тепловые двигатели. Цикл Карно. (Задачи: 7.7; 8.7; 9.7;10.7; 1.7; 2.7; 3.7; 4.7; 5.7; 6.7; 8.8; 9.8; 10.8;1.8; 2.8; 3.8; 4.8; 5.8; 6.8; 7.8.) В программу школьного курса физики входит ряд вопросов, связанных с тепловыми двигателями. Школьник должен знать основные принципы работы теплового двигателя, понимать определение коэффициента полезного действия (КПД) циклического процесса, уметь находить эту величину в простейших случаях, знать, что такое цикл Карно и его КПД. Тепловым двигателем (или тепловой машиной) называется процесс, в результате которого внутренняя энергия какого-то тела превращается в механическую работу. Тело, внутренняя энергия которого превращается двигателем в работу, называется нагревателем двигателя. Механическая работа в тепловых машинах совершается газом, который принято называть рабочим телом (или рабочим веществом) тепловой машины. При расширении рабочее тело и совершает полезную работу. Для того чтобы сделать процесс работы двигателя циклическим, необходимо еще одно тело, температура которого меньше температуры нагревателя и которое называется холодильником двигателя. Действительно, если при расширении газ совершает положительную (полезную) работу (левый рисунок; работа газа численно равна площади «залитой» фигуры), то при сжатии газа он совершает отрицательную («вредную») работу, которая должна быть по абсолютной величине меньше полезной работы. А для этого сжатие газа необходимо проводить при меньших температурах, чем расширение, и, следовательно, газ перед сжатием необходимо охладить. На среднем рисунке показан процесс сжатия газа 2-1, в котором газ совершает отрицательную работу A2-1, абсолютная величина которой показана на среднем рисунке более светлой «заливкой». Чтобы суммарная работа газа за цикл А1-2 + A2-1была положительна, площадь под графиком расширения должна быть больше площади под графиком сжатия. А для этого газ перед сжатием следует охладить. Кроме того, из проведенных рассуждений следует, что работа газа за цикл численно равна площади цикла на графике зависимости давления от объема, причем со знаком «плюс», если цикл проходится по часовой стрелке, и «минус» - если против.  Таким образом, двигатель превращает в механическую работу не всю энергию, взятую у нагревателя, а только ее часть; остальная часть этой энергии используется не для совершения работы, а передается холодильнику, т.е. фактически теряется для совершения работы. Поэтому величиной, характеризующей эффективность работы двигателя, является отношение  (15.1)где А - работа, совершаемая газом в течение цикла, QH - количество теплоты, полученное газом от нагревателя за цикл. Отношение (15.1) показывает, какую часть количества теплоты, полученного у нагревателя, двигатель превращает в работу и называется коэффициентом полезного действия (КПД) двигателя Если в течение цикла рабочее тело двигателя отдает холодильнику количество теплоты Qx (эта величина по своему смыслу положительна), то для работы газа справедливо соотношение A = QH-QX. Поэтому существует ряд других форм записи формулы (15.1) для КПД двигателя  (15.2) Французский физик и инженер С. Карно доказал, что максимальным КПД среди всех процессов, использующих некоторое тело с температурой T1 в качестве нагревателя, и некоторое другое тело с температурой Т2 (Т2< Т1) в качестве холодильника, обладает процесс, состоящий из двух изотерм (при температурах нагревателя T1 и холодильника Т2) и двух адиабат (см. рисунок).Изотермам на графике отвечают участки графика 1-2 (при температуре нагревателя T1) и 3-4 (при температуре холодильника Т2),адиабатам - участки графика 2-3 и 4-1. Этот процесс называется циклом Карно. КПД цикла Карно равен  (15.3)Теперь рассмотрим задачи. 1). |