Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
 Скачать 1.57 Mb.
|
|
(ответ – 4) В двух последних задачах этого варианта нужно с помощью закона Клапейрона- Менделеева вычислить один из параметров газа, если даны остальные параметры. 9). В задаче 1.3 из закона Клапейрона - Менделеева 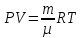 получим  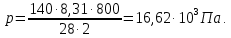 (ответ - 1). 10). В задаче 2.3 при вычислениях следует не забыт перевести температуру газа в Кельвины. Из закона Клапейрона - Менделеева находим 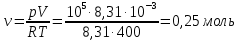 .(ответ - 1). 11). Задача 4.4. Из уравнения состояния в форме pV = NkT (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода р1 и гелия р2 равно 2. (ответ - 2). 12). Задача 5.4. Поскольку перегородка подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона - Менделеева, получим для гелия pVHe= 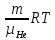 ,для азота 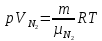 ,где температуры Т и массы газовm по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда 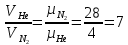 (ответ- 4) 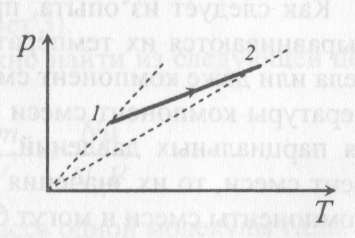 13). Задача 6.4. Если бы точки, отвечающие состояниям 1 и 2 лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу(13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром). Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед Т в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается V1 < V2. (ответ - 2). 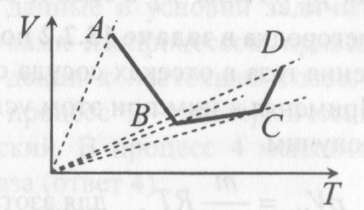 14). Задача 7.4. Аналогичные рассуждения показывают, что наибольшему давлению отвечает изобара, проходящая через точку С (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок). ответ - 3. 15). Задача 8.4. В закон Клапейрона - Менделеева входит абсолютная температура газа, поэтому данные в задаче значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном р2 и начальном p1состояниях получаем 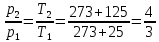 (ответ - 4). 16). Задача 9.4. Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов. Поэтому температуры компонент смеси будут одинаковы. (ответ - 1). 17). Задача 10.4. Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны. Парциальное давление компонент смеси - это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона - Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа р1 и гелия р2 в сосуде имеем р1/р2 =2. (ответ - 2). 18). Задача 1.4. Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции - один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция 2O3 → 3O2 т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза. (ответ - 2). 19). Задача 2.4. Поскольку объемы и температуры газов одинаковы, для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода Н2 (т.е. половина моля) и 3·1023 молекул гелия Не (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково. (ответ - 3). 20). Задача 3.4. Плотность газа можно найти из следующей цепочки формул 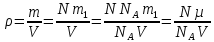 Здесь m - масса газа, m1 - масса одной молекулы газа. (ответ - 4). 3. Задания на проверку элементов знаний и умений по теме: термодинамика. ( Задачи: 5.5; 6.5; 7.5; 8.5; 9.5; 10.5; 1.5; 2.5; 3.5; 4.5; 6.6; 7.6; 8.6; 9.6; 10.6; 1.6; 2.6; 3.6; 4.6; 5.6.) Изучение энергетических превращений в молекулярных системах составляет содержание термодинамики. Для решения задач на термодинамику необходимо знать определения внутренней энергии, количества теплоты, теплоемкости и ряда других величин. Необходимо также понимать и уметь использовать в простейших случаях первый закон термодинамики как балансовое соотношение, описывающее процессы превращения энергии из одних форм в другие. Также нужно знать основные свойства процессов перехода вещества из одних агрегатных состояний в другие. Рассмотрим эти вопросы. Внутренней энергией тела называется сумма кинетической энергии молекул и потенциальной энергии их взаимодействия друг с другом. Для жидкостей и твердых тел из-за сильного взаимодействия молекул друг с другом вычислить внутреннюю энергию не удается. Внутреннюю энергию можно вычислить только для идеальных газов, в которых можно пренебречь энергией взаимодействия молекул друг с другом и считать, что внутренняя энергия равна сумме кинетических энергий молекул. Для одноатомного газа (т.е. газа, каждая молекула которого состоит из одного атома) внутренняя энергияU определяется соотношением 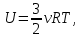 (14.1)где ν - количество вещества газа (число молей), R - универсальная газовая постоянная, Т - абсолютная температура. Заметим, что с помощью закона Клапейрона - Менделеева формула (14.1) может быть преобразована к виду 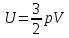 (14.2)где р - давление, V - объем газа. Внутренняя энергия тела может измениться при теплообмене, когда молекулы тела сталкиваются с более быстрыми или более медленными молекулами других тел и получают от них или отдают им энергию, или в процессе совершения механической работы над этим телом внешними силами. В связи с эти вводят следующие определения. Количеством теплоты, переданным некоторому телу, называют энергию, переданную этому телу в процессе хаотических столкновений молекул. Процесс передачи энергии в виде теплоты называют процессом теплопередачи. Если внешние силы не совершают над телом работы, для процесса теплопередачи справедливо следующее балансовое соотношение ΔU = Q (14.3) где ΔU - изменение внутренней энергии тела,Q - количество переданной этому телу теплоты. Поскольку изменение внутренней энергии тела может быть и положительным ΔU > 0, и отрицательным ΔU < 0, из закона (14.3) следует, что количеству теплоты следует придать алгебраический смысл: если энергия передается телу, количество переданной этому телу теплоты нужно считать положительным Q > 0, если забирается – отрицательным Q < 0. Внутренняя энергия тела изменяется при сжатии тела, трении и ряде других механических процессах. В этом случае на изменение внутренней энергии расходуется работа А , совершаемая над телом внешними силами ΔU = A (14.4) (конечно, здесь подразумевается, что работа А не расходуется на энергию движения тела как целого, а только на изменение внутреннего движения, т.е. все перемещения тела как целого или его макроскопических частей должны происходить бесконечно медленно). Очевидно, работа внешних сил положительна, если эти силы сжимают тело и его объем уменьшается, и отрицательна - если объем тела увеличивается. В первом случае, как это следует из (14.4), внутренняя энергия тела возрастает (ΔU > 0), во втором убывает (ΔU< 0). 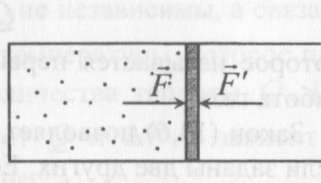 Одновременно с внешними силами при сжатии или расширении тел совершают работу и сами эти тела. Рассмотрим, например, газ, находящийся в цилиндрическом сосуде и отделенный от атмосферы поршнем (см. рисунок). И при сжатии, и при расширении газа силы, действующие на поршень со стороны газа, совершают над ним работу А (в первом случае отрицательную, во втором положительную). При этом, поскольку поршень перемещается бесконечно медленно, силы, действующие на него со стороны газа и внешние силы практически равны друг другу как при сжатии, так и при расширении газа (в противном случае в балансе энергии необходимо было учитывать кинетическую энергию, приобретенную поршнем). Поэтому работа, совершенная газом и внешними силами над газом равны по величине, но отличаются знаком. Очевидно, работа газа положительна, если газ расширяется, и отрицательна, если газ сжимается. (В этой связи отметим, что в термодинамике иногда используются следующие обозначения: работа газа обозначается как А,работа внешних сил над газом - как  . Нам кажется, что лучше таких обозначений не использовать – всё равно забудешь, у какой работы надо ставить штрих. Необходимо понимать разницу между этими величинами, а при чтении условия задачи и при проведении термодинамических рассуждений отдавать себе отчет, о какой работе идёт реч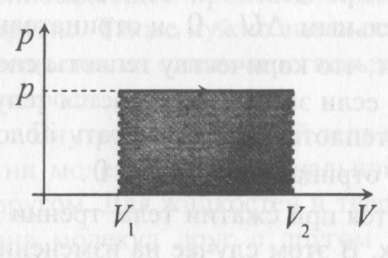ь). При решении задач на термодинамику следует помнить одно важное свойство работы газа, которое во многих случаях позволяет ее легко вычислить. Работа газа в некотором процессе численно равна площади фигуры под графиком зависимости давления от объема в этом процессе. В частности в изобарическом процессе при давлении р, в котором объем газа изменился от значения V1 до значения V2, газ совершает работу (см. рисунок; площадь графика, соответствующая работе, выделена): А = p(V2-V1) = pΔV = νRΔT, (14.5) где ν - количество вещества газа, ΔT - изменение температуры в рассматриваемом процессе. Если газ участвует в процессе, в котором одновременно имеет место и теплообмен, и совершается работа, то справедливо соотношение Q = ΔU + A,(14.6) которое называется первым законом термодинамики (здесь А - работа газа). Закон (14.6) позволяет найти одну из входящих в него величин, если заданы две других. Если задается только одна из величин, входящих в закон (14.6), но как-то определяется процесс, происходящий с газом, то две остальные величины могут быть определены. Например, в |