Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
 Скачать 1.57 Mb. Скачать 1.57 Mb.
|
КОММЕНТАРИИ К ОТВЕТАМ ПО МОЛЕКУЛЯРНОЙ ФИЗИКЕ.1. Задания на проверку элементов знаний и умений по теме: основные понятия и принципы молекулярно – кинетической теории. (Задачи: 1.1; 2.1; 3.1; 4.1; 5.1. 6.1; 7.1; 8.1; 9.1; 10.1; 2.2; 3.2; 4.2; 5.2; 6.2; 7.2; 8.2; 9.2; 10.2; 1.2.) В задания ЕГЭ по физике всегда включаются задачи, касающиеся основных принципов молекулярно-кинетической теории. Это задачи, связанные с молекулярной структурой газов, жидкостей и твердых тел, с определением температуры, с методами подсчета числа составляющих тело молекул. В этой главе собраны задачи, связанные с понятиями моля и температуры. Молем вещества называется такое количество этого вещества, которое содержит приблизительно 6·1023 молекул, причем независимо от того, какое это вещество (точнее 6,0221367·1023). Приведенное выше число молекул в моле называется числом Авогадро и обозначается как NA. Как правило, при решении задач считают, что NA= 6·1023. (12.1) Обратим внимание читателя на то, что моль - макроскопическое количество вещества (в переводе с латинского языка - языка средневековой науки - словоmoles означает толпа). Масса одного моля вещества называется молярной массой этого вещества. И поскольку массы молекул разных веществ - разные, а число молекул в моле разных веществ одинаковое, то молярные массы веществ различны. При этом отношение молярных масс двух веществ равно отношению масс их молекул. Поэтому массы молей пропорциональны массам молекул. Число Авогадро (12.1) было подобрано так, чтобы масса моля, выраженная в граммах, численно совпадала с массой молекулы, выраженной в атомных единицах массы (а.е.м.). Поэтому массы молей различных веществ легко найти из периодической системы химических элементов. Например, в таблице находим, что масса молекулы гелия - 4,0026 а.е.м., следовательно, масса моля гелия - 4,0026 ≈4 г, масса двухатомной молекулы кислорода - 31,986 а.е.м., следовательно, масса моля кислорода - 31,986 ≈ 32 г. Необходимо также знать определение температуры. Температура тела - величина, пропорциональная средней кинетической энергии молекулы 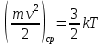 (12.2) (12.2)где (mv2/2)ср - средняя кинетическая энергия молекулы, Т - абсолютная температура (ее называют также температурой в шкале Кельвина), k - постоянная, которая называется постоянной Больцмана. Из формулы (12.2) следует, что температура по шкале Кельвина не может быть отрицательна, ее минимальное значение Т = 0 (абсолютный нуль температуры) достигается, когда все молекулы имеют нулевые кинетические энергии. 1 градус шкалы Кельвина (или просто один Кельвин) совпадает с градусом более привычной в быту шкалы Цельсия, нуль которой определяется как температура плавления льда, а температура 100 °С отвечает температуре кипения воды при атмосферном давлении. Как показывает опыт, абсолютному нулю температуры отвечает температура t = -273 °С. Важнейшее свойство температуры заключается в том, что при приведении тел в тепловой контакт их температуры через некоторое время выровняются и далее (в отсутствие теплообмена с окружающими телами) не будут изменяться. Рассмотрим теперь задачи. 1). Задача1.1. Поскольку число молекул в моле не зависит от того, какое это вещество, и равно числу Авогадро. (ответ_-_3).'>(ответ - 3). 2). Задача 2.1. Поскольку массы молекул разных веществ - разные, одинаковые массы разных веществ содержат различные количества молекул. Найти эти количества можно, зная молярные массы и число Авогадро. Например, в этой задаче можно провести такие рассуждения. Водород массой 1 г составляет половину моля, и, следовательно, содержит 6·1023 /2 = 3·1023 молекул. Кислород массой 1 г составляет 1/32 часть моля, и, следовательно, содержит (6·1023)/32 = (3/16) 1023 молекул. Отсюда находим отношение числа молекул N1 в 1 г водорода к числу молекул N2 в 1 г кислорода: N1 /N2 =16. (ответ - 1). 3). Задача 3.1. Согласно определению число молекул в моле одинаково для любого вещества, причем независимо от того, сколько атомов входят в состав одной молекулы этого вещества. Другими словами, это число не зависит от того, являются ли молекулы одно-, двух-, и т.д. атомными. (ответ– 4). 4). Задача 4.1. Поскольку число молекул в моле любого вещества равно числу Авогадро, то для молярной массы любого вещества µ справедливо соотношение: µ = NAm, где m - масса одной молекулы. Отсюда находим, что µ/m = NА. (ответ-1). 5). Задача 5.1. Чтобы понять, сколько молей содержит та или иная масса вещества, нужно разделить эту массу на молярную массу данного вещества (или число содержащихся в ней молекул на число Авогадро). Поскольку молярная масса гелия равна 4 г/моль, то 10 г гелия составляют 4/10 = 2,5 моль. (ответ - 1). 6). Задача 6.1. Для характеристики числа молекул в некоторой массе вещества принято использовать величину, которая называется количество вещества. Эта величина определяется как число молей, составляющих данную массу. Для нахождения количества вещества нужно разделить число молекул этой массы вещества на число Авогадро, (или саму массу на молярную массу данного вещества). Поскольку в задаче газ в сосуде содержит 3·1023 молекул, то количество вещества газа составляет 0,5 моль. (ответ - 2). 7). Задача 7.1. Как указывалась во введении к настоящей главе, молярные массы веществ можно найти по периодической таблице элементов. Масса моля, выраженная в граммах, численно совпадает с массой молекулы, выраженной в атомных единицах массы (а.е.м.). Из приведенной в условии задачи клетки таблицы, отвечающей рутению, находим массу молекулы рутения µ = 101,07 а.е.м. (второе число в клетке, которое для всех элементов является обязательно целым, представляет собой порядковый номер элемента). Поэтому для рутения находим: µ = 101,07 ≈101 г/моль. (ответ - 2). 8). Задача 8.1. Связь температуры и средней кинетической энергии молекул определяется формулой (12.2). (ответ - 2). 9). Задача 9.1. Температурой плавления льда (и замерзания воды) является температура 0 °С. Поскольку нуль шкалы Кельвина (абсолютный нуль температуры) в шкале Цельсия составляет -273 °С (см. введение к настоящей главе), то температура плавления льда по абсолютной шкале равна 273 К. (ответ - 3) 10). Задача 10.1. Изменением температуры тела в некотором процессе называется разность его конечной и начальной температур тела Тк- Тн . Так как температуры в шкале Цельсия и Кельвина связаны «сдвигом»: Т (К) = t (°С) + 273 (К), то разность температур в градусах Кельвина Т (К) и в градусах Цельсия Т (°С) совпадает. Другими словами, изменение температуры тела одинаково при задании температуры как в шкале Кельвина, так и в шкале Цельсия. (ответ – 2). 11). В задаче 2.2 нужно снова использовать определение количества вещества. Напоминаем, что количеством вещества называется число молей, составляющих данную порцию вещества. Отсюда находим количество вещества, водорода νH2 =mH2/µH2=1/2 = 0,5 моль и количество кислорода νO2 =mO2/µO2= 8 /32 = 0,25 моль в сосудах. Поэтому νH2 > νO2 (ответ - 1). 12) Задача 3.2. Из периодической таблицы элементов имеем для масс атомов: тH = 1 а.е.м., mN = 14 а.е.м., т0 = 16 а.е.м. Отсюда находим массу молекулы азотной кислоты mHNO3 =1 + 14 + 3-16 = 63 а.е.м. Поэтому µНNОз = 63 г/моль. (ответ - 4). 13). Задача 4.2. Масса одной молекулы углерода тс= 12 а.е.м. А поскольку моль углерода содержит 6·1023, то масса моля углерода равна 12·6 1023 = 72·1023а.е.м. (ответ - 1). 14). Задача 5.2. Поскольку молярная масса - это характеристика вещества, то, находя эту величину, можно определить вещество. Плотность газа ρ (масса единицы объема) и концентрация молекул n (число молекул в единице объема), очевидно, связаны друг с другом через массу одной молекулы т: ρ = пт. Умножая правую и левую Часть этой формулы на число Авогадро и учитывая, что NA·т = µ, получим µ = NA·ρ / п = 4 г/моль. Поэтому неизвестный газ – гелий. (ответ - 2). 15). Задача 6.2. Используя определение температуры (12.2), получим для средней скорости молекул водорода  . .(ответ - 3). 16). Задача 7.2. Из определения температуры (12.2) следует, что при повышении температуры в 2 раза средняя скорость молекул увеличивается в  раз. раз.(ответ - 3). 17). Задача 8.2. При приведении газов в тепловой контакт их температуры выровняются. Отсюда согласно определению температуры следует, что средние кинетические энергии молекул газов станут равными:  или v1 = v/4. или v1 = v/4.(ответ - 3). 18). Задача 9.2.. Используя определение температуры (12.2) для каждого газа и учитывая, что независимо от того, сколько атомов входит в состав молекулы, в правую часть определения температуры (12.2) входит коэффициент 3/2, получим  где v1 - средняя скорость молекул водорода, v2 - средняя скорость молекул гелия. Поскольку масса молекулы гелия в два раза больше массы молекулы водорода, то  . .(ответ - 2). 19). Задача 10.2. Поскольку моль любого вещества содержит одинаковое количество молекул, то для сравнения числа молекул воды и ртути в стакане можно сравнить число молей. Число молей воды и ртути в стакане найдем из следующих цепочек формул. Воды:  (1) (1)Ртути:  (2) (2)гдеmиρ- массы и плотности веществ, µ - молярные массы, V - объем стакана. Сравнивая величины (1) и (2), заключаем  (здесь использованы плотности и молярные массы воды и ртути). Поэтому в стакане ртути больше молекул, чем в стакане воды, причем в 67/55 = 1,2 раза. |
