Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124

• Название: Учебное пособие для подготовки к Единому Государственному Экзамену. Под редакцией профессора, доктора педагогических наук, директора моу Лицей 13 С. А. Старченко. Троицк 2016. 124
• Дата: 09.01.2023
• Размер: 1.57 Mb.
• Имя файла: posobie_f.docx
• Тип: Учебное пособие; #878255
• страница: 18 из 27

8. Задания на проверку элементов знаний и умений по теме:

гидростатика
(Задачи: 8.8; 9.8; 10.8; 11.8; 12.8; 13.8; 13.8; 14.8; 15.8; 16.8;17.8; 18.8; 19.8; 20.8; 1.8; 2.8; 3.8; 4.8; 5.8; 6.8; 7.8.)

Для решения задач на гидростатику необходимо знать определения плотности и давления, уметь находить давление в покоящейся жидкости, возникающее благодаря притяжению этой жидкости к Земле (гидростатическое давление), а также находить силы, с которыми жидкости действуют на погруженные в них пела (силу Архимеда). Кратко сформулируем эти определения и законы.

Плотностью тела называется отношение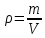

(9.1)

где m - масса тела, V - его объем. Очевидно, отношение (9.1) имеет смысл массы единицы объема тела. Если тело однородно, то плотность (9.1) является характеристикой не тела, а вещества, из которого оно состоит. Действительно, для тел, состоящих из одного и того же вещества масса пропорциональна объему, и отношение (9.1) одинаково у всех этих тел.

Для характеристики воздействия жидкости или газа на стенки сосудов вводят понятие давления жидкости или газа, которое определяется как отношение силы F, действующей на элемент стенки сосуда со стороны жидкости или газа, к величине площади этого элемента ΔS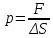

(9.2)

Важным свойством давления является то обстоятельство, что хотя оно и определяется через элемент площади стенки сосуда, от этого элемента давление (9.2) не зависит, а является характеристикой только жидкости или газа. Действительно, сила, действующая со стороны жидкости на элемент площади дна сосуда или стенки сосуда, пропорциональна площади этого элемента, и потому отношение (9.2) от ΔS не зависит. Отметим, что хотя давление и определяется через векторную величину - силу, давление - величина не векторная.

Как показывает опыт, отношение (9.2) не зависит не только от величины площадки ΔS, но и от ее ориентации в пространстве. Другими словами, жидкость, будучи сжатой, оказывает воздействие во всех направлениях. Последнее утверждение и говорит о невекторном характере давления и называется законом Паскаля.

В жидкости, находящейся в каком-либо сосуде в поле силы тяжести, благодаря ее притяжению к Земле, возникает давление. Это давление называется гидростатическим. Можно доказать, что гидростатическое давление жидкости не зависит от формы сосуда, в котором она находится, а зависит только от глубины.

Гидростатическое давление жидкости плотности ρ на глубине h равно

p = ρgh (9.3)

где g - ускорение свободного падения. Если на поверхность жидкости действует атмосферный воздух, то давление жидкости на глубине h будет складываться из атмосферного давления и гидростатического давления (9.3).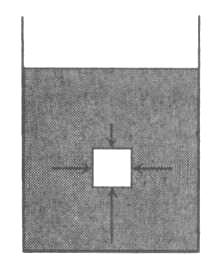

Благодаря зависимости гидростатического давления жидкости от глубины возникает своеобразный эффект выталкивания тел, погруженных в жидкость, из этой жидкости. Действительно, в жидкости, находящейся в поле силы тяжести, возникает гидростатическое давление, и жидкость оказывает воздействие на поверхность тела, опущенного в жидкость. При этом силы, действующие на боковые поверхности тела, компенсируют друг друга.

Однако из-за зависимости гидростатического давления от глубины, сила, действующая на более глубокую (нижнюю) поверхность тела, больше силы, действующей на верхнюю поверхность (см. рисунок), и на тело действует результирующая сила, направленная вертикально вверх. Эта сила называется выталкивающей силой или силой Архимеда. Можно доказать, что на тело, целиком погруженное в жидкость, действует выталкивающая сила

F = ρgV (9.4)

где ρ - плотность жидкости, V - объем тела. Если тело погружено в жидкость не целиком, то выталкивающая сила также определяется формулой (9.4), но вместо объема тела в нее входит объем погруженной в жидкость части тела.

С помощью формулы (9.4) можно установить условие плавания тел. Тело будет плавать, если сила Архимеда будет больше действующей на тело силы тяжести

ρgV > mg = ρ₁gV,

где ρ₁ - плотность тела. Отсюда получаем, что тело плавает, если плотность жидкости больше плотности тела ρ > ρ₁ (9.5)
Рассмотрим теперь задачи.

1). В задаче 8.8 с использованием формулы (9.3) для гидростатического давления находим

р = 1000·10·200 = 2·10⁶ Па.

(ответ - 4)

2). Задача 9.8. Поскольку высота уровней жидкости в сосудах и их плотности одинаковы, то давление жидкости около дна обоих сосудов одинаково.

(ответ - 3).

3). Задача 10.8. Давление жидкости около дна сосудов одинаково (одинаковы плотности и уровень жидкостей), поэтому сила, действующая на дно, больше для того сосуда, площадь дна которого больше, а меньше для того, площадь дна которого меньше.

Поэтому F₁ < F₂ < F₃

(ответ - 2).

4). Задача 11.8. Чтобы найти силу, действующую на небольшую поверхность внутри жидкости, нужно найти гидростатическое давление жидко­сти на той глубине, на которой находится рассматриваемая поверхность, и умножить это давление на площадь поверхности. Поэтому для крана получаем

p = ρghS = 1000·10·2·1·10^-4 = 2 Н

(ответ - 4).

5). Задача 12.8. Бытовой насос поднимает воду благодаря создаваемому им избыточному давлению. Ясно, что вода в трубках насоса будет подниматься до тех пор, пока ее гидростатическое давление не компенсирует избыточное давление насоса. Поэтому насос сможет поднять воду на следующую высоту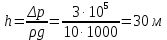



где Δр - избыточное давление, созданное насосом, ρ - плотность воды, g -ускорение свободного падения.

(ответ - 3).

6). Задача 13.8. Поскольку бруски изготовлены из одинакового материала, у них одинаковые плотности, и, следовательно, отношение их масс равно отношению их объемов. А поскольку объем второго бруска вчетверо больше объема первого, то и его масса вчетверо больше массы первого, т.е. равна 40 г.

(ответ - 3).

7) Задача 14.8. Пусть размер меньшего ребра бруска - а. Тогда размеры остальных сторон - 2а и 3а. Следовательно, площади граней бруска равны 2а², 3а² и 6а². Поэтому давления бруска на стол, когда он лежит на разных гранях, равны (начиная с наименьшего):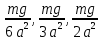



т.е. относятся друг к другу так же, как и длины сторон 1:2:3.

(ответ - 1).

8). Задача 15.8. В сообщающихся сосудах жидкость занимает такое положение, что ее давление в обоих коленах одинаково. Поэтому имеем с использованием формулы для гидростатического давления

ρ₁g(a-b) + ρ₂gb = ρ₂gc.

Отсюда находим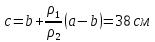

.

(ответ - 4).

9). Задача 16.8. Поскольку плотность натрия 950кг/м³меньше плотности воды 1000 кг/м³, то натрий плавает на поверхности воды.

(ответ 1)

10). Задача 17.8. На льдину действуют сила тяжести и сила Архимеда. Условие равновесия льдины дает

ρgV_П.Ч = mg (1)

где ρ - плотность воды, V_пч - объем погруженной в воду части льдины, m - ее масса. Поскольку m = ρ₁V, где ρ₁ - плотность льда, V - объем льдины, из формулы (1) получаем

ρV_П.Ч = ρ₁V

Отсюда находим, что отношение объема погруженной в воду части льдина к ее объему равно отношению плотностей льда и воды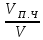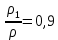

=

Таким образом, девять десятых частей плавающей льдины находятся под водой.

(ответ - 2).

11). Задача 18.8. Поскольку тело плавает в жидкости, выталкивающая сила Архимеда равна действующей на тело силе тяжести - 10 Н.

(ответ - 1).

12). Задача 19.8. Весом тела Р называется сила, с которой тело действует на опору (сила реакции опоры). На тело, полностью погруженное вводу, действуют сила тяжести mg, выталкивающая сила Архимеда ρ₀gV и сила реакции. Для силы реакции (веса тела) из условия равновесия тела имеем

P = mg - ρ₀gV = (ρ₁ - ρ₀)gV,

где ρ₀ и ρ₁ - плотности жидкости и тела, V - объем тела (обратим внимание читателя на то, что согласно этой формуле вес тела в жидкости уменьшается). Отсюда находим



(ответ - 3).

13). Задача 20.8. Из условия равновесия коробки, плавающей на поверхности воды, следует, что сила тяжести равна силе Архимеда mg = ρgV_nч, где m - масса тела, ρ - плотность воды, V_nч – объем погруженной части коробки, который можно выразить через площадь дна коробки и глубину его погружения в воду V_пч = Sh = 50 см³. Отсюда получаем для массы коробки m = 500 г.

ответ - 2).

14). Задача 1.8. При решении школьники часто допускают ошибку, говоря, что выталкивающая сила равна нулю, так как шар, наполненный воздухом, находясь в воздухе, «всплывать» не будет. Последнее утверждение, конечно, правильно, а первое - нет. Шар, наполненный воздухом, не «всплывает» в воздухе не потому, что выталкивающая сила не действует, а потому, что она меньше силы тяжести. Выталкивающая сила действует на тело со стороны жидкости или газа и никак не может зависеть от того, что внутри этого тела, воздух или, например, гелий, с которым шар всплывал бы. Для выталкивающей силы имеем согласно закону Архимеда

F= ρgV = 1,29 10 0,01 = 0,129 Н.

(ответ - 1).

15). Задача 2.8. На поплавок действуют силы: тяжести , Архимеда , натяжения лески (см. рисунок). Используя стандартное выражение для силы Архимеда (9.4), получаем из условия равновесия поплавка

T = ρ₀gV – mg

где ρ₀ - плотность воды, m и V - масса и объем поплавка. Выражая массу поплавка через его плотность и объем m = ρV и учитывая, что по условию плотность воды вдвое больше плотности поплавка ρ₀ = 2ρ , получим

Т = ρgV= mg = 10 Н