Учебно-методический комплекс по ДКБ. Учебное пособие для студентов по направлениям подготовки 080100. 62 Экономика 080100. 6201 Мировая экономика
 Скачать 2.18 Mb. Скачать 2.18 Mb.
|
1.4. Основы теории стоимости денег во времени1.4.1. Функции сложного процента Принятие решения о вложении капитала определяется в конечном счете величиной дохода, который инвестор предполагает получить в будущем. Временная теория стоимости денег исходит из предположения, что деньги, являясь специфическим товаром, со временем меняют свою стоимость и, как правило, обесцениваются. Изменение со временем стоимости денег происходит под влиянием целого ряда факторов. Важнейшими факторами можно назвать инфляцию и способность денег приносить доход при условии их разумного инвестирования в альтернативные проекты. Основными операциями, позволяющими сопоставлять разновременные деньги, являются операции накопления и дисконтирования. Накопление - процесс определения будущей стоимости денег. Дисконтирование – процесс приведения денежных поступлений от инвестиций к их текущей стоимости. На этих двух операциях строится весь финансовый анализ, одним из основных критериев которого является процентная ставка i. В случае выполнения операции накопления эта ставка называется ставкой дохода на капитал, при дисконтировании – ставкой дисконта или ставкой дисконтирования. Это расчетные инструменты, которые могут быть применены для оценки прогнозируемых доходов от инвестиций. Перед их использованием следует определить: 1) суммы денежных средств, о которых может идти речь; Общим знаменателем суммы являются наличные доллары или их денежные эквиваленты. Важно с максимально возможной точностью спрогнозировать общую сумму долларов, которые, как ожидается, будут инвестированы или получены от инвестиций. Это позволит ответить на главный вопрос: обеспечит ли данное вложение средств положительную ставку дохода? Положительная ставка дохода на инвестиции ожидается в тех случаях, когда приток денежных средств должен превысить их отток. Однако даже известные с абсолютной точностью суммы ничего не говорят о том, какой будет ставка дохода или связанный с вложением риск. 2) время, когда эти суммы должны быть выплачены или получены; Время для инвестора является одним из наиболее ценных и незаменимых ресурсов. Будучи потерянным, оно не может быть восполнено. Непродуктивно использованное время означает потерю денег. Единственный способ избежать этого – заставить капитал работать, т.е. вложить его в дело. Деньги используются для того, чтобы приносить процент. Важно время получения последнего, поскольку уже полученный процент может быть использован для извлечения еще большего процента. Время получения инвестиционного дохода измеряется интервалами, или периодами. Интервал, или период, может быть равен дню, неделе, месяцу, кварталу, полугодию, году. Время, в течение которого должны быть выплачены или получены деньги, имеет первостепенное значение в любом инвестиционном анализе. 3) осознанные риски, связанные с инвестициями; Под риском понимается непостоянство и неопределенность, связанные с инвестициями. Иными словами, риск – это вероятность того, что доходы, которые будут получены от инвестиций, окажутся больше или меньше первоначально прогнозируемых. Аналитику следует помнить, что существуют различные виды риска и что ни одно из вложений не является абсолютно безрисковым. 4) соответствующую ставку дохода (ставку процента или дисконта) с учетом рыночных условий и оцененного риска. Ставка дохода на инвестиции – процентное соотношение между чистым доходом и вложенным капиталом. Правильно определенная ставка дохода учитывает суммы и время получения ожидаемых чистых доходов. Данный показатель может быть использован как общий знаменатель при сопоставлении различных инвестиционных предложений. Ставка дохода на инвестиции называется также конечной отдачей. Применительно к потребительским кредитам это "ежегодная процентная ставка". За исключением случаев, когда в оценке инвестиций используются критерии нефинансового характера, приоритет отдается тем вложениям, по которым ставка дохода наиболее высока. Однако, если все элементы инвестиционных предложений различны, прогнозируемые ставки дохода сопоставляются с риском. Чем больше риск, тем выше должна быть ставка дохода для того, чтобы она могла компенсировать риск инвестору. Поскольку расчеты с использованием сложного процента носят чисто механический характер, а также вследствие того, что структура доходов от инвестиций может быть различной, для разных ставок процентов подготовлены специальные таблицы. Каждая страница таблиц рассчитана по крайней мере на 30 лет и содержит 6 колонок. Таблицы разработаны для годового, ежеквартального, полугодового и ежемесячного начисления процента. На практике для удобства расчетов используются специальные финансовые калькуляторы, имеющие ряд с пятью клавишами для финансовых расчетов: клавиша N – число периодов; клавиша %I – периодическая ставка процента; PMT – периодический платеж; PV – текущая стоимость суммы и FV - будущая стоимость суммы. Финансовые расчеты могут основываться на простом или сложном проценте. Разница в расчетах по простому и сложному проценту заключается в том, что при простом проценте ставка начисляется каждый раз на первоначально вложенный капитал, при сложном проценте каждое последующее начисление ставки осуществляется от накопленной в предшествующий период суммы. Все дальнейшие рассуждения будут построены на эффекте сложного процента. Процентная ставка задается, как правило, как номинальная годовая ставка. В том случае, если начисление процента осуществляется чаще, чем один раз в год рассчитывается эффективная годовая ставка по следующей формуле: где: i – номинальная годовая ставка, k – число начислений в году. Чем чаще производится начисление процента, тем выше эффективная годовая ставка Временная оценка денежных потоков основана на использовании шести функций сложного процента. 1.4.2. Накопленная сумма единицы Первая функция: накопленная сумма денежной единицы (будущая стоимость единицы) Данная функция используется в том случае, если известна текущая (сегодняшняя) стоимость денег и требуется определить ее накопленную сумму на конец определенного периода при заданной ставке дохода на капитал. Базовые формулы: а) при начислении процентов 1 раз в год: б) при более частом начислении процентов: где к – число лет. Для примерного определения срока удвоения капитала (в годах) существует правило «72-х», в основу которого положены логарифмы. Для расчета необходимо 72 разделить на целочисленное значение годовой ставки дохода на капитал. Правило применимо для ставок дохода на капитал в интервале 3-18%. 1.4.3. Текущая стоимость единицы Вторая функция: текущая стоимость единицы (реверсии). Смысл задач такого класса состоит в том, чтобы при заданной ставке дисконта дать оценку текущей стоимости тех денег, которые могут быть получены в конце определенного периода. Поскольку деньги обладают стоимостью во времени, один доллар, который будет получен в будущем, стоит меньше доллара, получаемого сегодня. Насколько меньше (сумма дисконта), зависит от: а) разрыва во времени между оттоком и притоком денежных средств; б) необходимой ставки процента или дисконта. Базовые формулы: а) при начислении процентов 1 раз в год: б) при более частом начислении процентов: 1.4.4. Обычный аннуитет Третья функция: текущая стоимость аннуитета. Аннуитет – это серия равновеликих платежей (поступлений) отстоящих друг от друга на один и тот же промежуток времени. Принято различать обычный и авансовый аннуитеты. В том случае, если платежи (поступления) производятся в конце каждого периода, говорят об обычном аннуитете. Базовые формулы: а) при платежах (поступлениях) в конце каждого года:  б) при более частых, чем один раз в год, платежах (поступлениях): 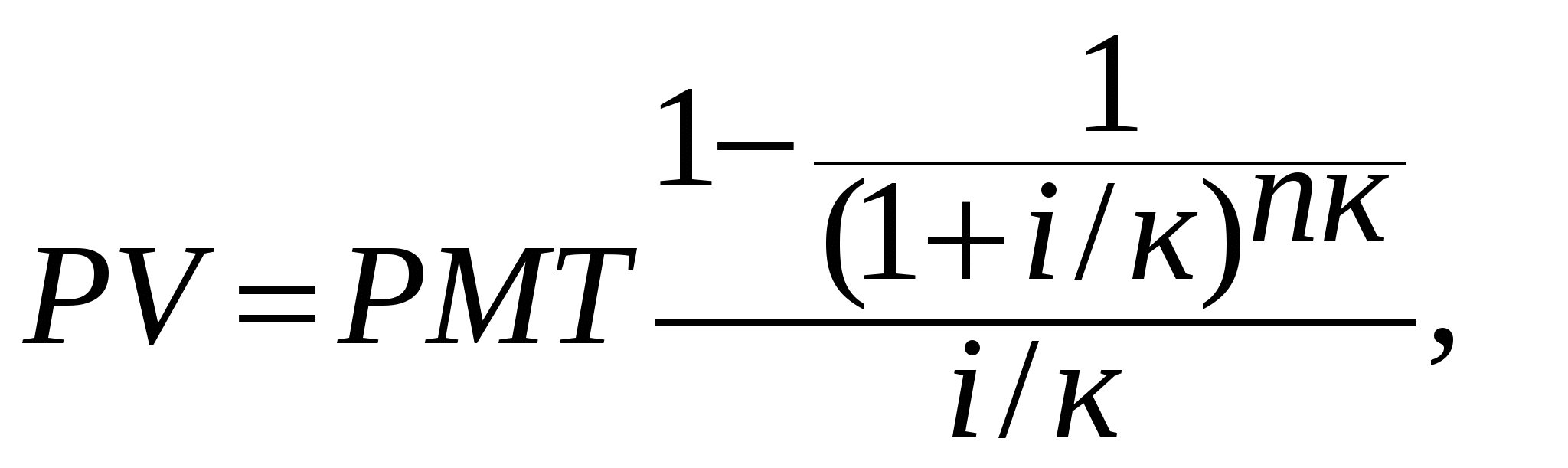 На практике возможна ситуация, когда первый платеж произойдет одновременно с начальным поступлением, т.е. в начале каждого периода. Последующие платежи производятся через равные интервалы. Такие аннуитеты называются авансовыми или причитающимися. Для того, чтобы определить текущую стоимость подобного аннуитета, необходимо проследить движение денежного потока. Поскольку первый аннуитет по времени совпадает с депонированием основного вклада, его не следует дисконтировать. Все последующие аннуитеты дисконтируются в обычном порядке, однако период дисконтирования всегда будет на единицу меньше. Следовательно фактор текущей стоимости авансового аннуитета соответствует фактору обычного аннуитета для предыдущего периода, к которому добавлена единица. Это добавленная единица обеспечивает заданный поток аннуитета. Базовые формулы: а) при платежах (поступлениях) в конце каждого года: 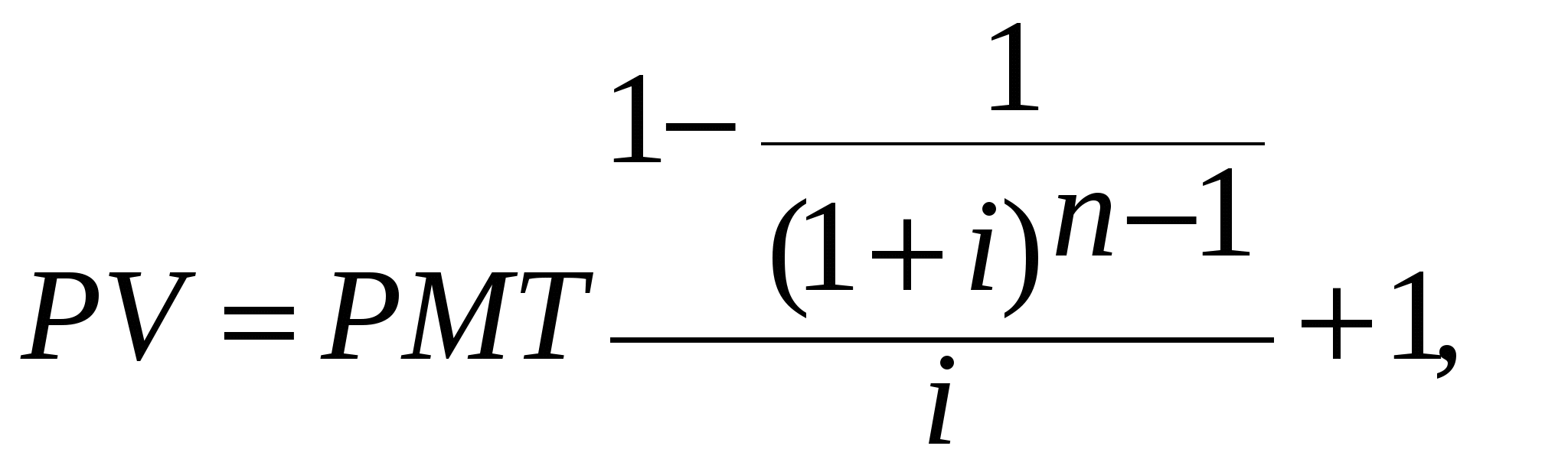 б) при более частых, чем один раз в год, платежах (поступлениях):  1.4.5. Авансовый аннуитет Четвертая функция: накопление денежной единицы за период. На основе использования данной функции определяется будущая стоимость серии равновеликих периодических платежей (поступлений). Аналогично условиям, рассмотренным в предыдущей функции, платежи (поступления) могут осуществляться как в конце, так и в начале каждого временного периода. Расчет будущей стоимости обычного аннуитета. Базовые формулы при платежах в конце периода: а) при платежах (поступлениях), осуществляемых 1 раз в конце года: б) при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год: Расчет будущей стоимости авансового аннуитета. Базовые формулы: а) при платежах (поступлениях), осуществляемых 1 раз в начале года: б) при платежах (поступлениях), осуществляемых чаще, чем 1 раз в год: 1.4.6. Взнос на амортизацию единицы Пятая функция – взнос на амортизацию единицы. Данная функция используется для определения аннуитетных (регулярных равновеликих) платежей в счет накопления кредита, выданного на определенный период при заданной ставке по кредиту. Функция взноса на амортизацию единицы обратно пропорциональна функции текущей стоимости обычного аннуитета. Базовые формулы: а) при платежах, осуществляемых 1 раз в год: 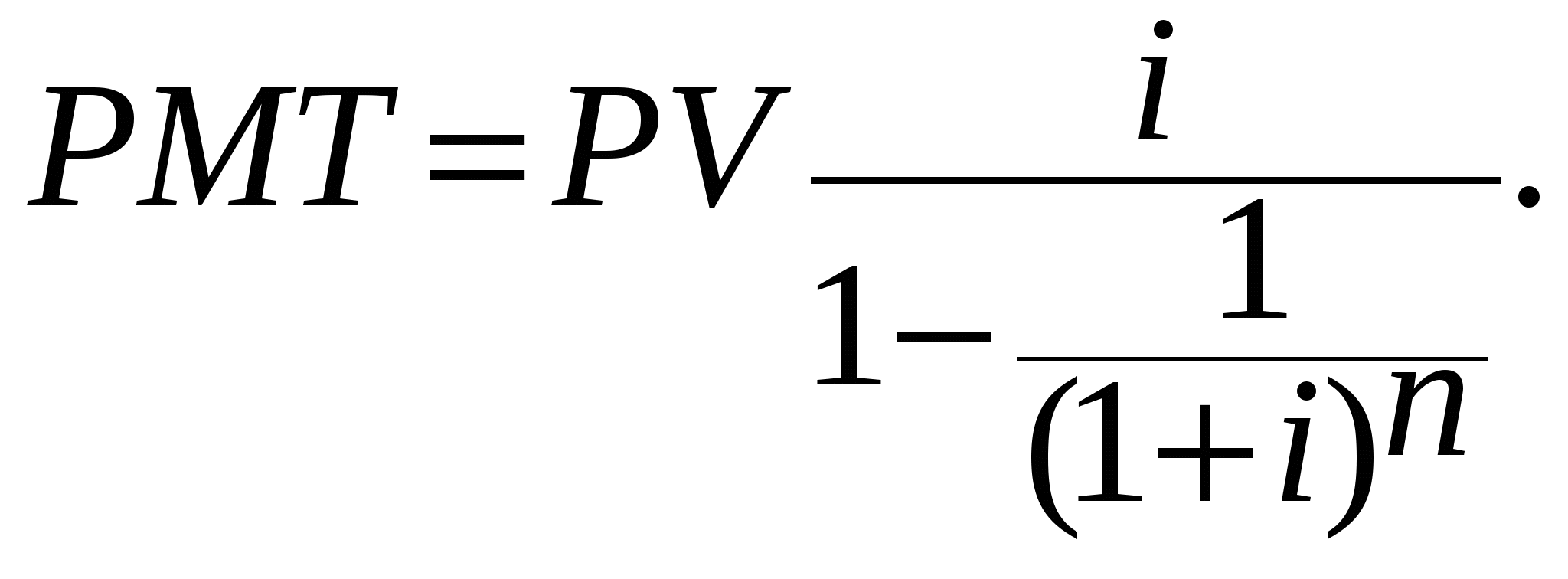 б) при платежах, осуществляемых чаще, чем 1 раз в год. 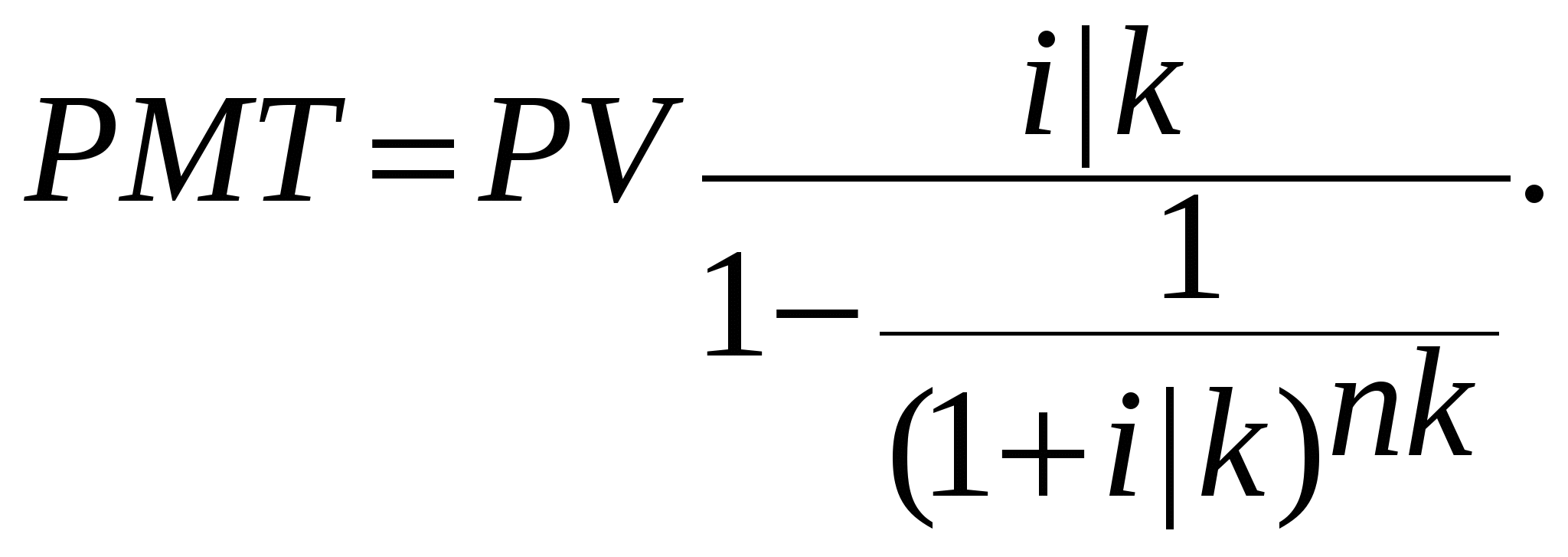 1.4.7. Фактор фонда возмещения Шестая функция – формирование фонда возмещения. Данная формула используется для определения тех равномерных периодических платежей, которые необходимо осуществлять в течение заданного периода, чтобы к концу срока иметь на счете, приносящем доход по заданной ставке, определенную сумму денег. Часто в тех случаях, когда вплоть до истечения срока долгового обязательства кредитору выплачивается только процент, заемщики для погашения основной суммы кредита создают специальные фонды возмещения. В течение каждого периода должник вносит в отдельный фонд сумму, которая вместе с начисляемым на нее процентом должна обеспечить погашение основной части кредита. С истечением срока задолженности фонд закрывается, а его остаток используется для погашения кредита. Фактор фонда возмещения – это величина, обратная фактору накопления единицы за период. Базовые формулы: а) при платежах, осуществляемых 1 раз в год: 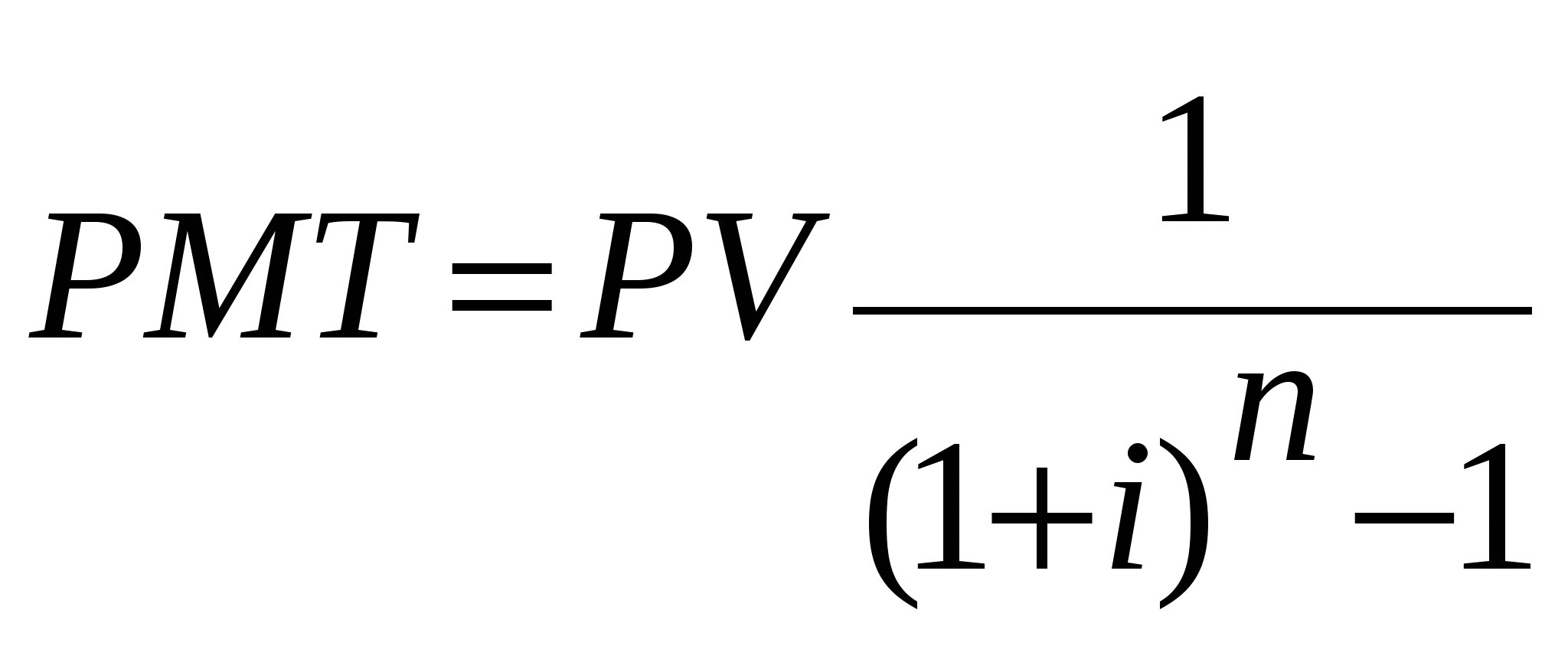 б) при платежах, осуществляемых чаще, чем 1 раз в год. 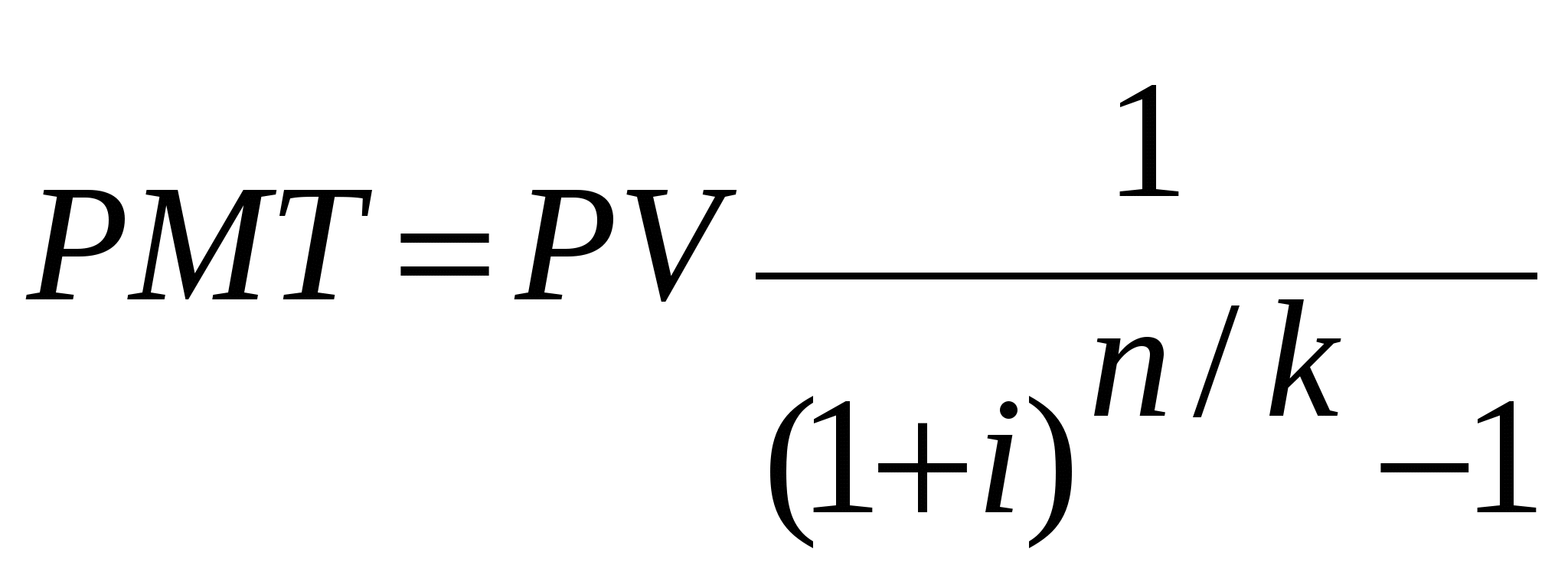 Расчет факторов всех шести функций основан на использовании базовой формулы сложного процента, главным условием, обеспечивающим математическую взаимосвязь между функциями, является предположение, что начисленный процент не снимается с депозитного счета и капитализируется. Шесть функций сложного процента могут быть использованы для решения почти всех арифметических задач, связанных с оценкой приносящих доход объектов недвижимости. Контрольные вопросы
|
