ПособФХпроцЧ.2ГидросфХОС05. Учебное пособие Физикохимические процессы в гидросфере
 Скачать 31.55 Mb.
|
5.2. Взаимосвязь между окислительно-восстановительнымии кислотно-основными характеристиками природных водПеренос электрона в редокс-процессе сопровождается переносом протона, обусловливая тем самым для реакций, протекающих в водном растворе, жесткую взаимосвязь между окислительно-восстановитель-ным и кислотно-основным равновесием. Например, если ион Fe(II) отдает электрон, то выделяются три иона водорода, что приводит в конечном результате к образованию труднорастворимого гидроксида железа (III) и увеличению концентрации ионов водорода в растворе: [  Fe(H2O)6]2+ Fe(OH)3 + 3Н2О + 3Н+ +  (78)Протеканием этой реакции объясняется кислый характер шахтных вод и образование характерного осадка «ржавчины» в местах выхода на поверхность подземных вод, содержащих ионы двухвалентного железа. Величина окислительно-восстановительного потенциала реакций, протекающих с участием ионов водорода или гидроксила, зависит от рН раствора. Одной из форм представления таких зависимостей являются диаграммы  – рН или диаграммы Eh– рН. Диаграммы эти идентичны, за исключением шкалы оси ординат, масштаб которой изменяется в соответствии с уравнением (75). При температуре 298 К Eh= 0,0591 . Недостаток использования Ehв качестве переменной состоит в том, что наклоны границ различных полей устойчивости зависят от температуры, чего удается избежать в случае, когда переменной является .Рассмотрим принципы построения диаграммы – рН на примере окислительно-восстановительных реакций, определяющих пределы существования или, как принято говорить, устойчивости воды.Вода может окисляться 2Н2О О2 + 4Н+ + 4 (79)либо восстанавливаться: 2Н2О + 2 H2 + 2OH– (80)Реакции (79) и (80) определяют пределы изменения в воде. Совершенно очевидно, что рН оказывает влияние на характеристики обеих реакций.Перепишем уравнение (79) в виде:  O2 + H+ +  Н2О (81)Константу равновесия этой реакции можно представить уравнением:  (82)В качестве граничных условий при описании пределов устойчивости воды обычно принимают давление кислорода 101 кПа (1 атм), при этом Р(кисл) = 1. Активность воды также можно принять равной единице. В этом случае уравнение (82) можно представить в виде:  = 1/(Кан+) (83)Прологарифмировав уравнение (2.83), умножим его левую и правую части на минус единицу; заменив выражения отрицательных логарифмов активности электронов и ионов водорода на и рН, получим:=lgK – pH (84)Величину логарифма константы равновесия этой реакции легко найти из значения энергии Гиббса образования молекул воды, поскольку Gобразования кислорода, ионов водорода и электронов по термодинамическим конвенциям принимаются равными нулю, поэтому lg К =  (85)Отсюда зависимость от рН при парциальном давлении кислорода, равном 1 атм, будет иметь вид: = 20,8 – рН. (86)В общем случае получим: =20,8+ – pH. (87)Уравнение (87) определяет окислительную границу устойчивости воды. При заданном значении рН для воды, находящейся в равновесии с атмосферным кислородом, ( )0 не может быть более положительным, чем величина, определяемая уравнением (87).Путем аналогичных рассуждений можно получить зависимость 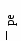– рН для восстановительной границы устойчивости воды: (88)  ; (89) (90)  Рис. 4. Зависимость окислительно-восстановительного потенциала (для различных природных вод) и пределов устойчивости воды от рН Поскольку Gреакции (88) равно нулю, то и значение логарифма константы равновесия этой реакции равно нулю. Поэтому при граничных условиях, когда парциальное давление водорода равно 1 атм, получаем уравнение: = –рН. (91)Природные воды обычно находятся в контакте с воздухом, в котором парциальные давления кислорода и водорода меньше 1 атм, поэтому их окислительно-восстановительные потенциалы будут находиться в интервале значений, определяемых уравнениями (86) и (91). На рисунке 4 представлены зависимости величины от рН для различных природных вод, имеющих большое распространение. Однако следует отметить, что в отсутствие катализаторов разложение воды протекает очень медленно. Поэтому вода может иметь текущие значения более положительные, чем окислительный предел (например, при растворении хлора в воде), или более отрицательные, чем восстановительный предел, описывающие равновесную ситуацию.Диаграммы – рН (Eh– рН) являются удобным способом изобра-жения областей устойчивости окисленных и восстановленных форм определенных окислительно-восстановительных систем. Каждый отрезок прямой на диаграмме отвечает зависимости от рН для определенной реакции. Если величина не зависит от рН, отрезки параллельны оси абсцисс. Вертикально расположенные отрезки не связаны с протеканием окислительно-восстановительных реакций, обычно они определяют границы областей фазовых переходов. В областях, где значение определяется величиной рН, отрезки расположены наклонно. Тангенс угла наклона определяется отношением количества ионов водорода и электронов, принимающих участие в данной реакции. Следует отметить, что диаграммы – рН и Eh– рН строятся при определенных значениях концентраций реагирующих компонентов и изменение концентраций приводит к изменению границ соответствующих областей.Как уже отмечалось выше, в реальных природных водах окислительно-восстановительные процессы протекают при участии бактерий. В каждой из окислительно-восстановительных реакций участвует свой тип бактерий, и реакции протекают в строгой последовательности. Раньше протекают реакции, обеспечивающие бактериям наибольшую энергию, т. е. те реакции, для которых в данных условиях окислительно-восстановительный потенциал имеет наибольшее значение. Поэтому при построении обобщающих – рН и Eh – рН диаграмм рассматриваются все возможные для данной системы окислительно-восстановительные процессы, но на диаграмму в конечном итоге наносятся лишь те, которые отвечают более высоким редокс-уровням. Частный случай построения и демонстрация возможности использования диаграмм – рН для определения областей существования отдельных компонентов системы Fe — О — Н2О рассмотрены в Примере 20. |