|
Ххх. Учебное пособие Капранов Б. И., Коротков М. М., Короткова И. А. Издательство Томского политехничекого университета 2004
В ультразвуковой дефектоскопии для контроля материалов и изделий используются преобразователи, возбуждающие в объекте контроля волны различных типов в зависимости от поставленной задачи. Акустическая волна проходя через границу раздела двух сред частично отражается, а частично проходит. Знание углов преломления и отражения в зависимости от угла ввода позволяет изготавливать преобразователи, возбуждающие в объекте контроля необходимую волну.
Также важными характеристиками, определяющими количественно долю пройденной и отраженной волны, являются коэффициенты отражения R и прохождения (прозрачности) D.
ГРАНИЦА ДВУХ ПОЛУБЕСКОНЕЧНЫХ СРЕД
Падающая на границу двух сред акустическая волна частично проходит через границу, а частично отражается от нее. При этом может происходить трансформация типов волн. В общем случае на границе двух твердых сред (рис. 6) возникают по две (продольная и поперечная) отраженных и преломленных волны.
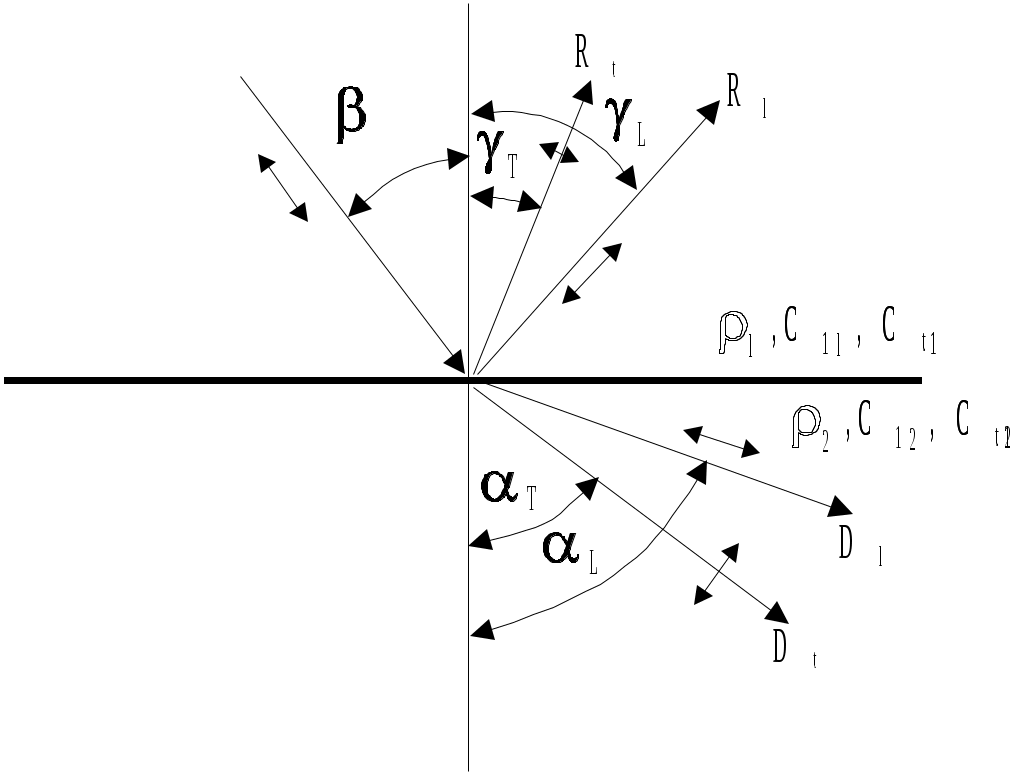
Рис. 6 Отражение и преломление волн на границе двух твердых тел
Направления отраженных и прошедших волн определяются из закона синусов:
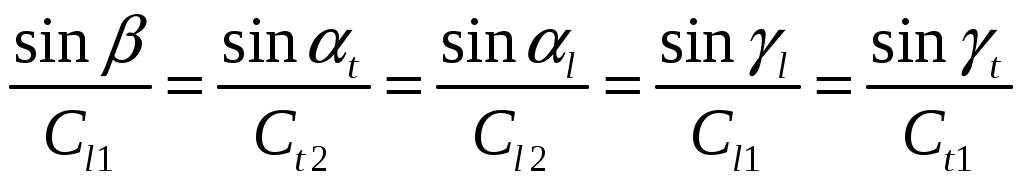 (1) (1)
где 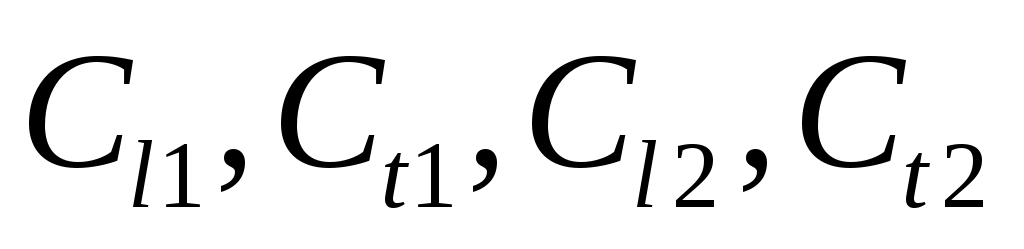 - скорости распространения продольных и поперечных волн в верхней и нижней средах. - скорости распространения продольных и поперечных волн в верхней и нижней средах.
Этот закон следует из равенства фазовых скоростей вдоль границы для всех волн.
Угол отражения продольной волны будет равен углу падения (т.к. падает продольная волна и скорости падающей и отраженной продольных волн равны).
Т.к. скорость распространения поперечной волны 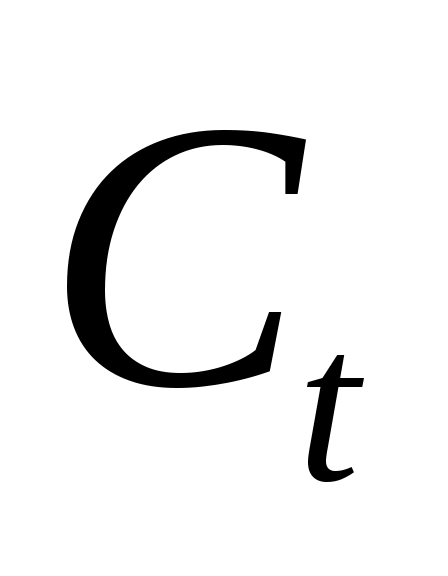 меньше (2 раза) чем меньше (2 раза) чем 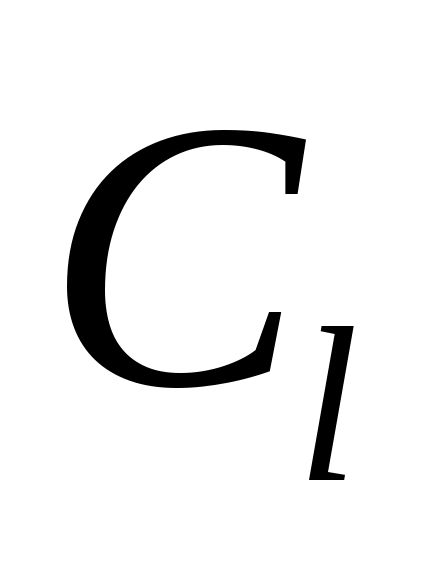 , то поперечная волна отразится под углом , то поперечная волна отразится под углом 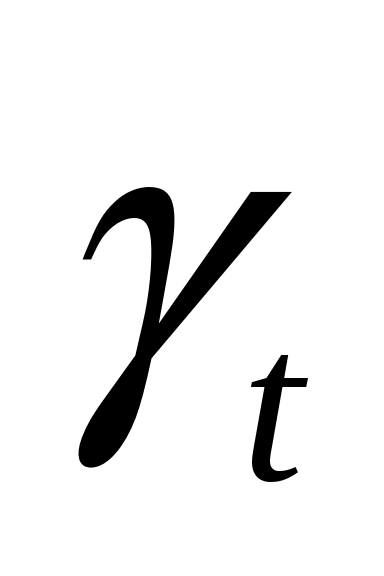 , меньшим, чем , меньшим, чем 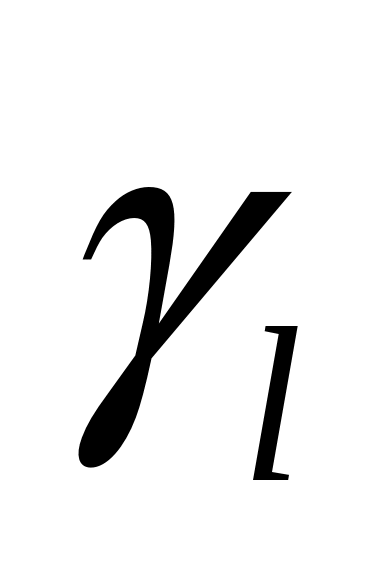 . .
Прошедшие продольные и поперечные волны также будут преломляться под разными углами, причем 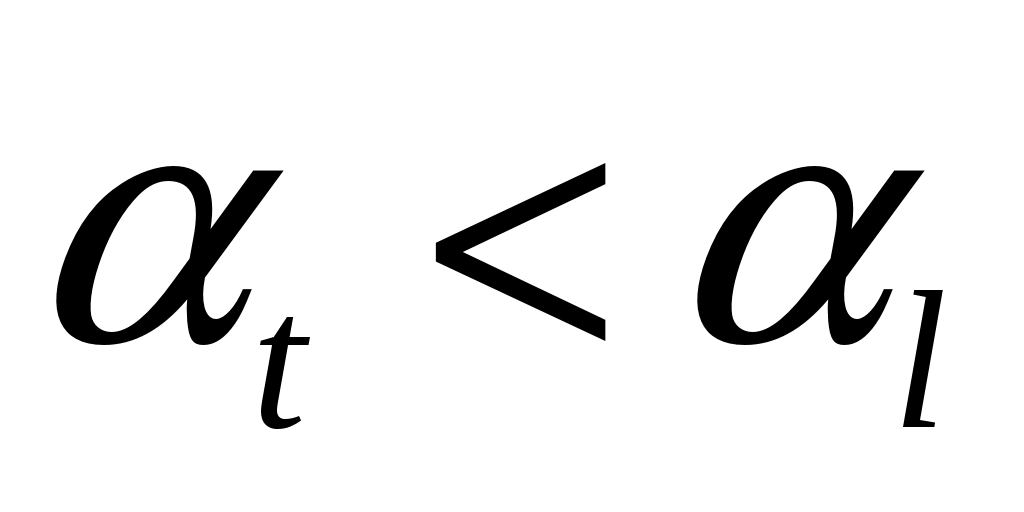 . При увеличении угла падения углы и будут увеличиваться и при некотором значении кр1 (первый критический угол) преломленные продольные волны будут распространяться по поверхности, не проникая вглубь среды, а преломленная поперечная волна будет уходить вглубь среды, что видно из рисунка 7, а. . При увеличении угла падения углы и будут увеличиваться и при некотором значении кр1 (первый критический угол) преломленные продольные волны будут распространяться по поверхности, не проникая вглубь среды, а преломленная поперечная волна будет уходить вглубь среды, что видно из рисунка 7, а.
При дальнейшем увеличении угла до значения кр2 (второй критический угол) по поверхности пойдут поперечные (сдвиговые волны), как показано на рисунке 7, б.
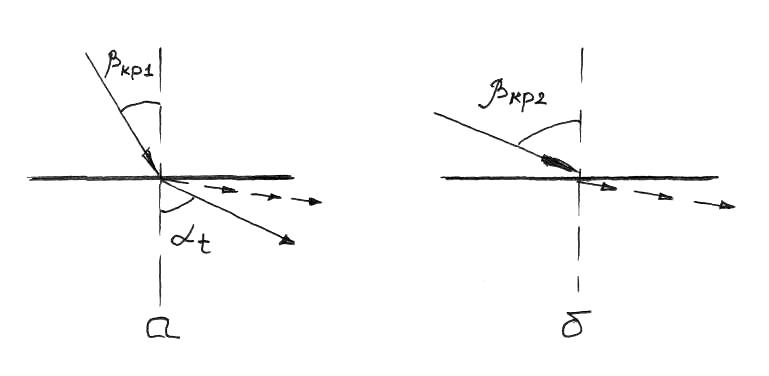
Рис. 7
Если построить график зависимости углов 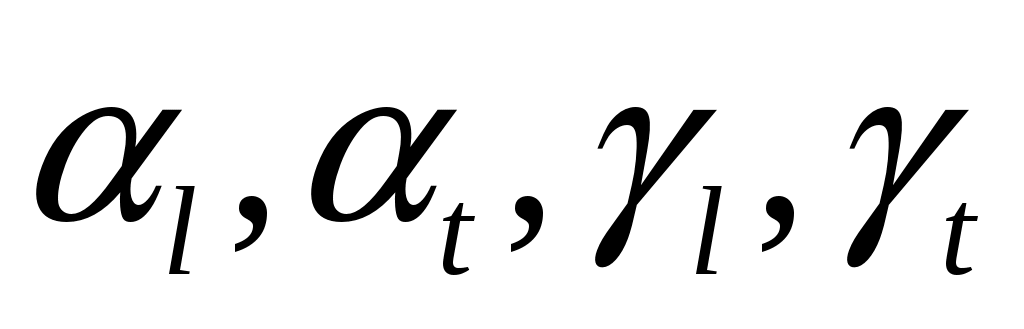 от угла падения , то он будет иметь вид, представленный на рисунке 8. от угла падения , то он будет иметь вид, представленный на рисунке 8.
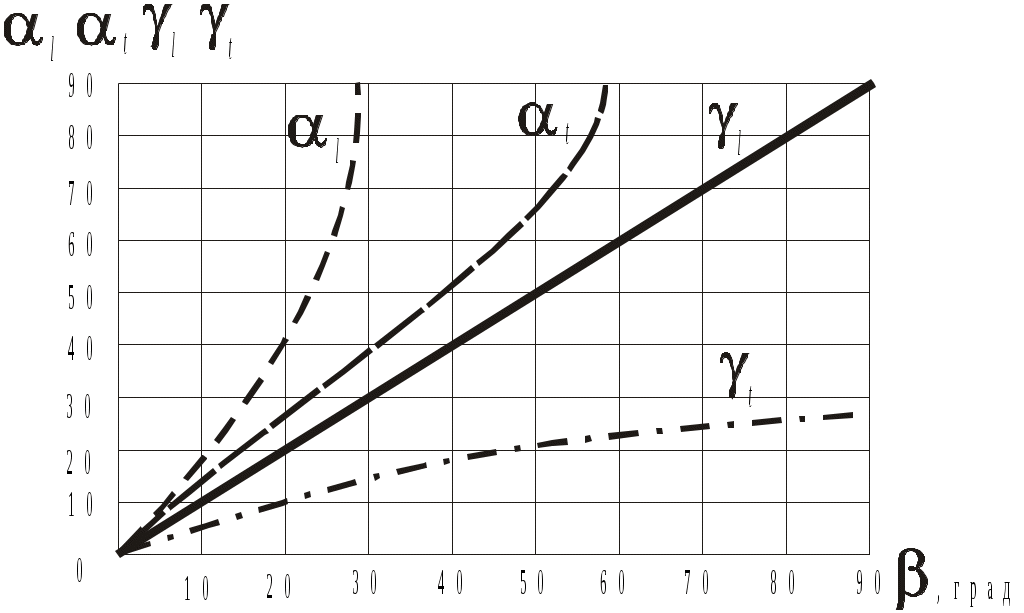
Рис. 8
Такой график строится для конкретного материала и позволяет быстро определять значения углов распространения отраженных и преломленных волн в средах в зависимости от .
При =0 расщепления падающей продольной волны на продольную и поперечную, отражение волны не происходит. Увеличение угла от 0 до 900 вызывает трансформацию падающей продольной волны, в результате чего в первой среде возникают отраженные, а во второй среде – преломленные продольные поперечные волны.
При малых углах поперечные (сдвиговые) волны очень слабы, однако с увеличением угла происходит перераспределение звуковой энергии, вследствие чего интенсивность поперечной волны увеличивается.
Для оргстекла при <270 во второй среде нельзя получить поперечных, а при >570 – продольных волн. Эти углы соответствуют кр1 и кр2 (для оргстекла), при которых происходит полное внутреннее отражение УЗК, падающих на поверхность раздела двух сред.
Амплитуда прошедшей Апр и отраженной Аотр волн характеризуются соответствующими коэффициентами прозрачности
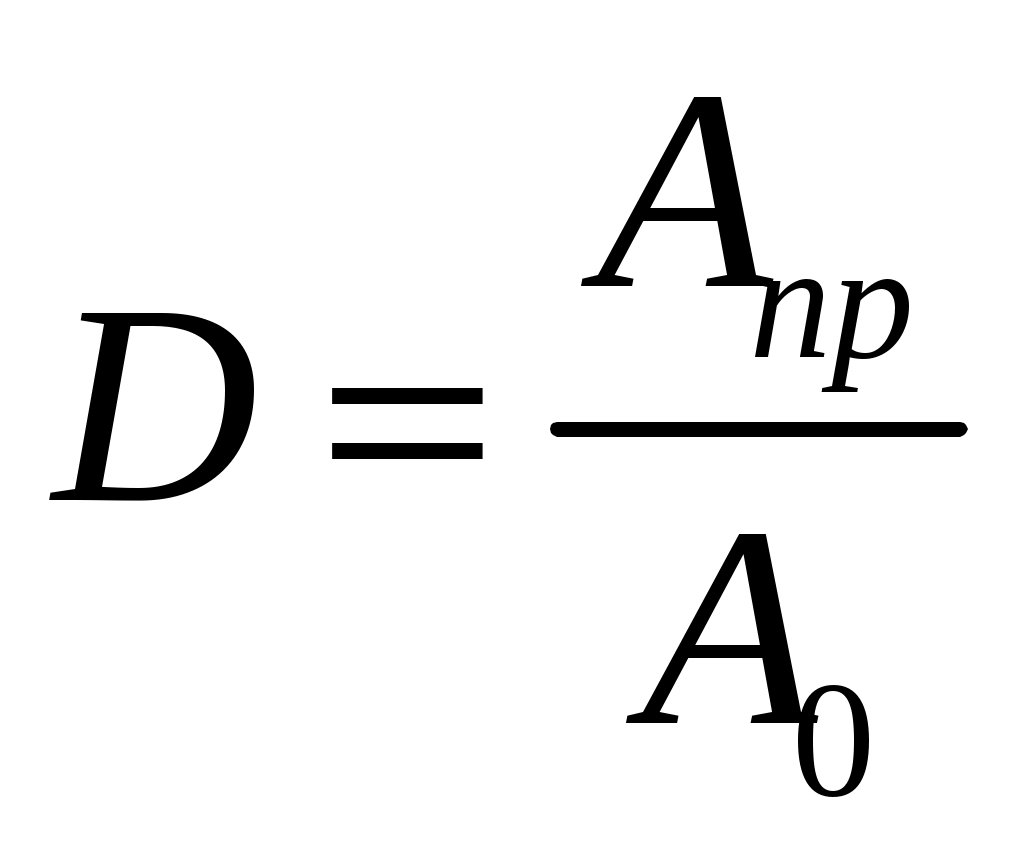 (2) (2)
и отражения
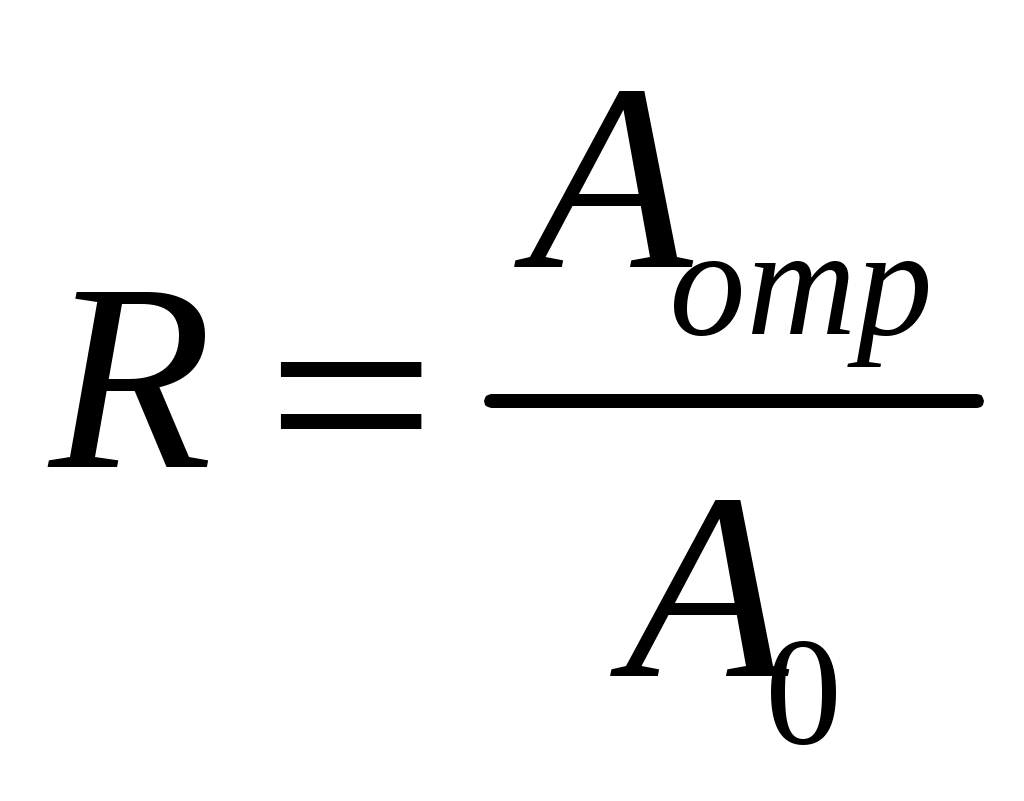 (3) (3)
где А0 - амплитуда падающей волны.
При решении задач о поведении волн на границе сред эффективно использовать понятие нормального импеданса границы. Рассмотрим вначале случай жидких или газообразных сред. Нормальный импеданс волны здесь определяют как отношение акустического давления к нормальной составляющей колебательной скорости
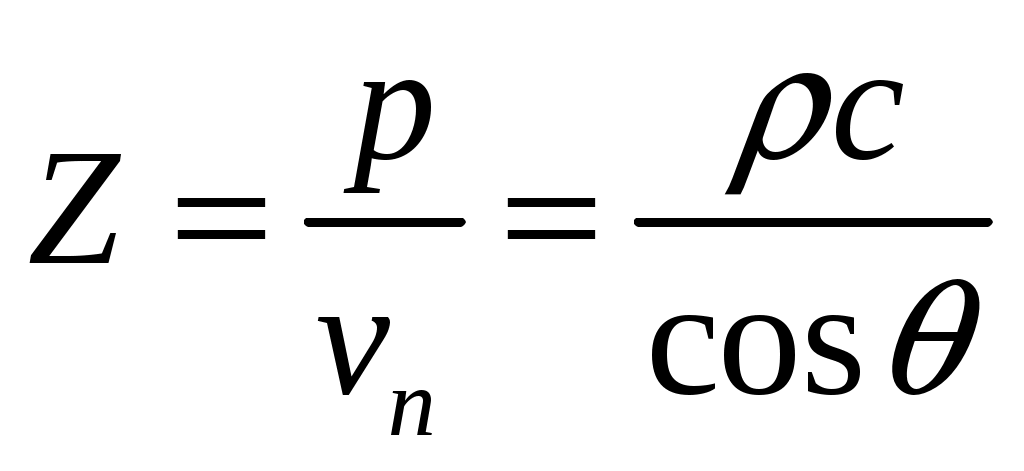 (4) (4)
где - угол между осью х и направлением волны.
Для расчета коэффициентов прозрачности и отражения имеются два граничных условия: равенство давлений и нормальных составляющих колебательной скорости сверху и снизу от границы. Из них следует, что при х = 0 суммарные импедансы волн сверху и снизу от границы равны:
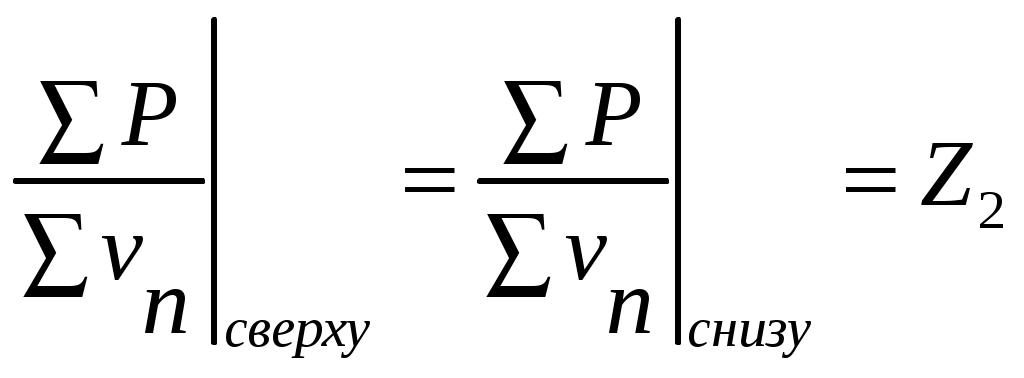 (5) (5)
Из данной формулы с учетом соотношения (1) и обозначая давление в отраженной волне р0R, найдем
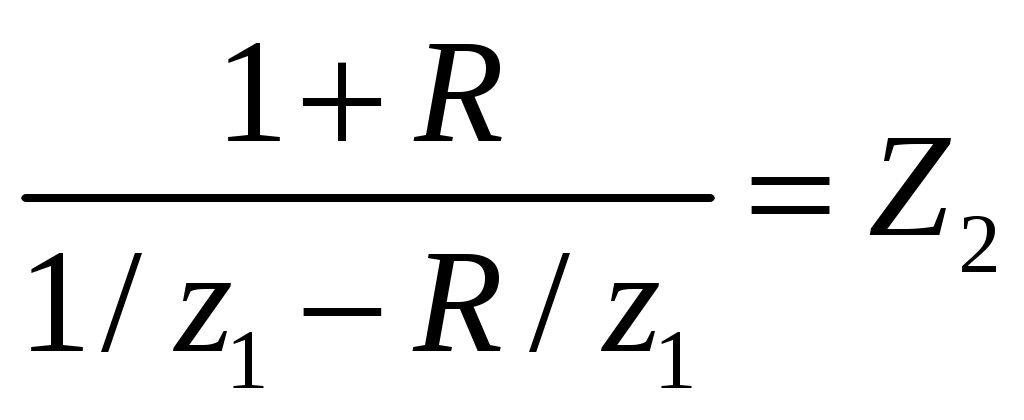 (6) (6)
Решая относительно R, получим
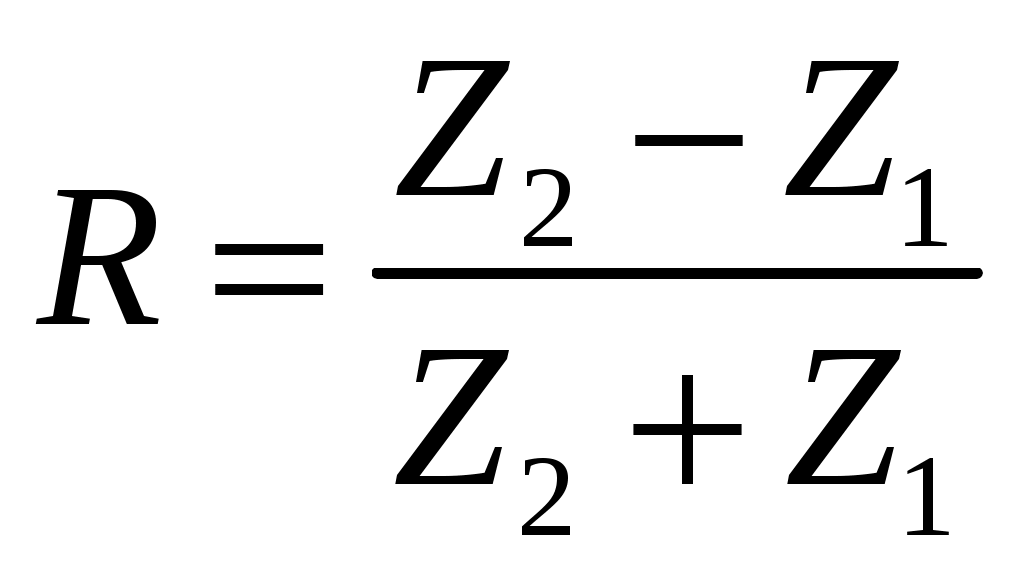 (7) (7)
Снизу от границы в рассматриваемом случае 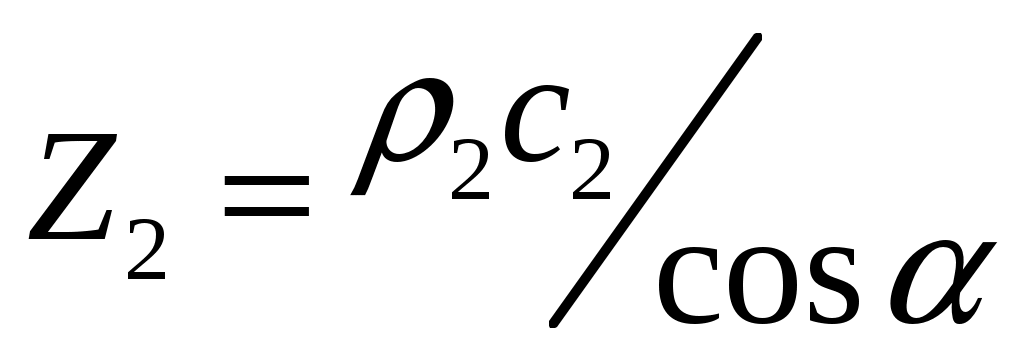 , поэтому , поэтому
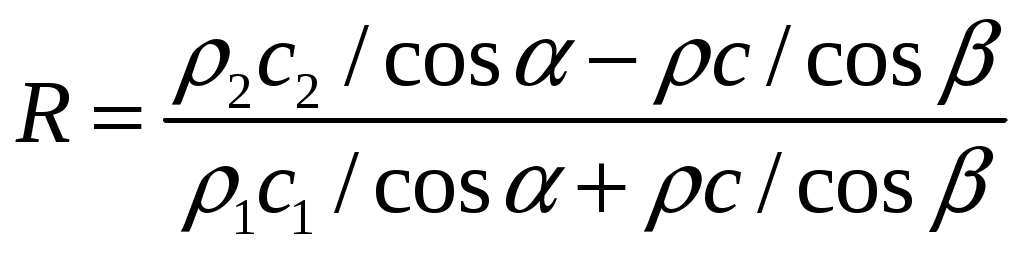 (8) (8)
В дальнейшем рассмотрим случаи, когда импеданс границы Z2 характеризуется более сложными выражениями, однако формула (7) останется справедливой. Используя закон равенства импедансов сверху и снизу от границы (его можно получить из равенства давлений при х=0), получим 1 + R = D. Отсюда 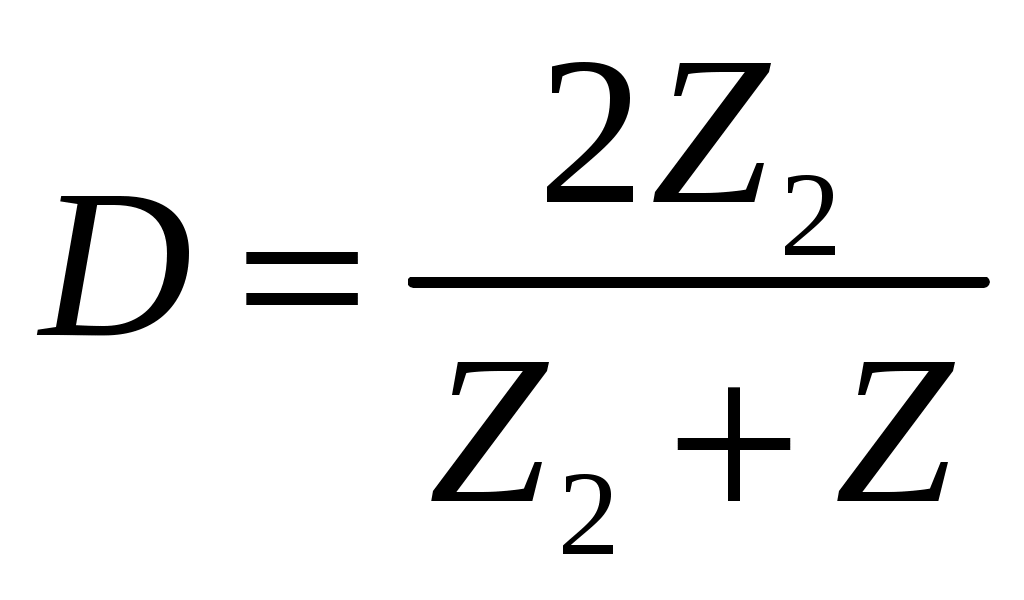 (9) (9)
Рассмотрим соотношение энергии падающей и преломленной волн. Интенсивность звука 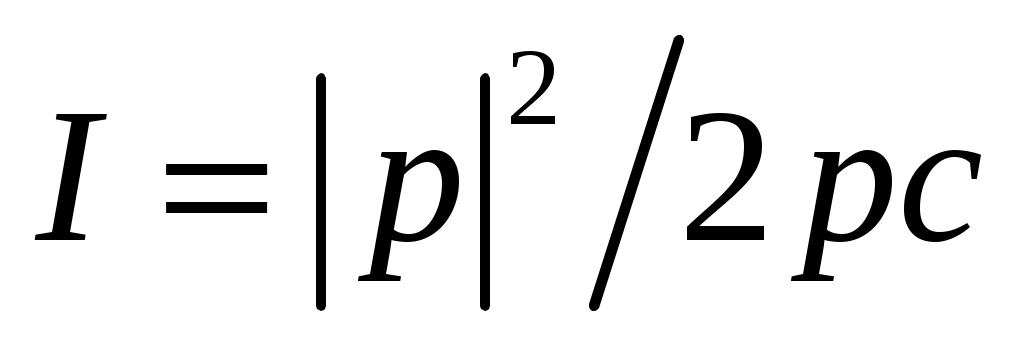 . Для определения доли прошедшей и отраженной энергии можно выделить компоненту потока энергии, нормальную к границе. Эти компоненты для падающей и преломленной волн соответственно равны: . Для определения доли прошедшей и отраженной энергии можно выделить компоненту потока энергии, нормальную к границе. Эти компоненты для падающей и преломленной волн соответственно равны: 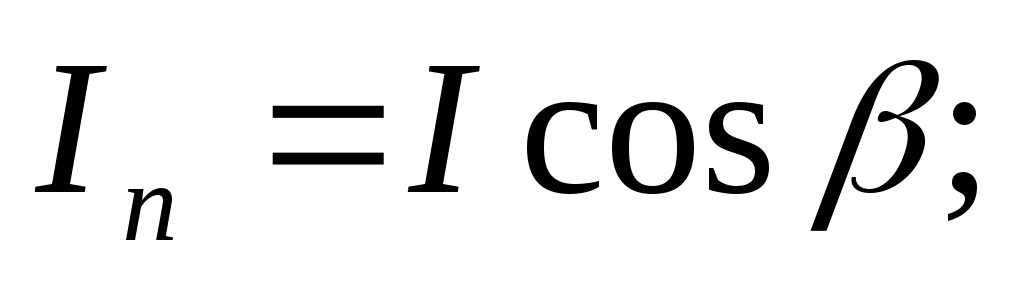 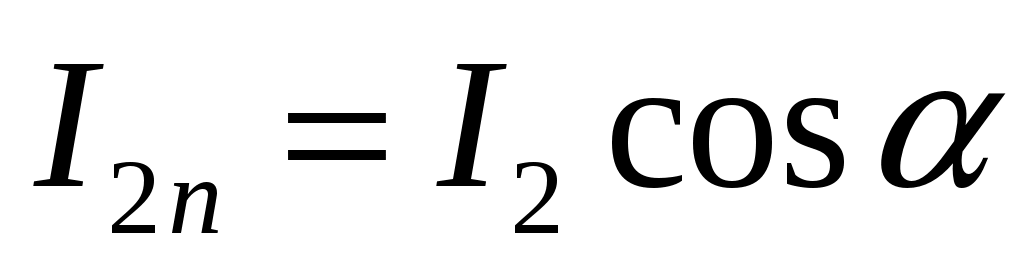 . Отсюда коэффициент прозрачности по энергии . Отсюда коэффициент прозрачности по энергии
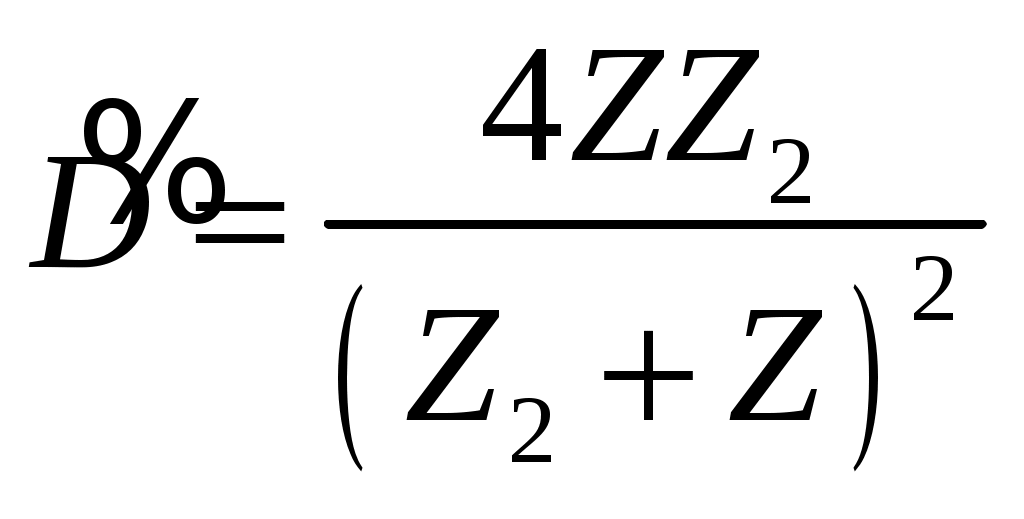 (10) (10)
Сопоставление со значением D по амплитуде давления показывает, что 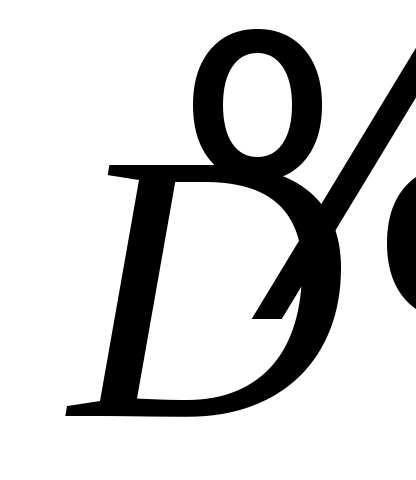 равен произведению величин D при прохождении через границу в прямом и обратном направлениях. Это положение важно для дефектоскопии, поскольку при введении акустических в объект контроля через какую-либо промежуточную среду волна обычно проходит через границу в двух направлениях; оно сохраняется для границ любых сред. Коэффициент отражения по интенсивности равен произведению величин D при прохождении через границу в прямом и обратном направлениях. Это положение важно для дефектоскопии, поскольку при введении акустических в объект контроля через какую-либо промежуточную среду волна обычно проходит через границу в двух направлениях; оно сохраняется для границ любых сред. Коэффициент отражения по интенсивности 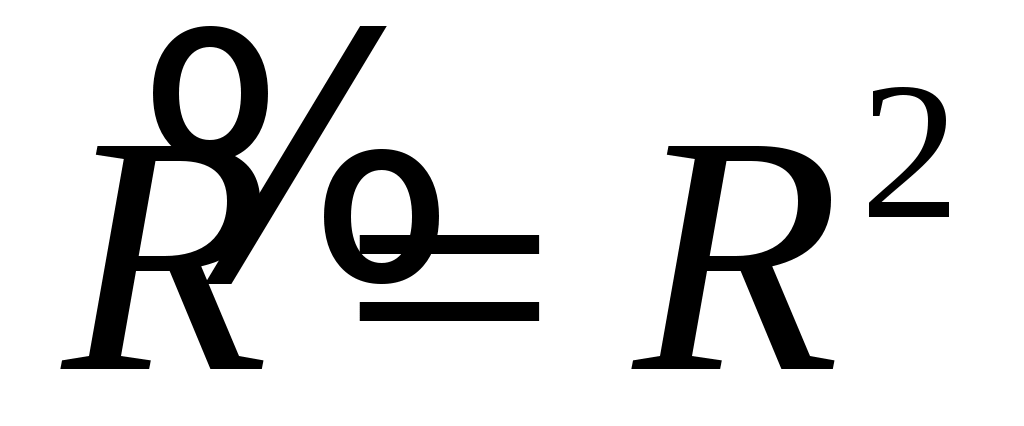 и равен и равен
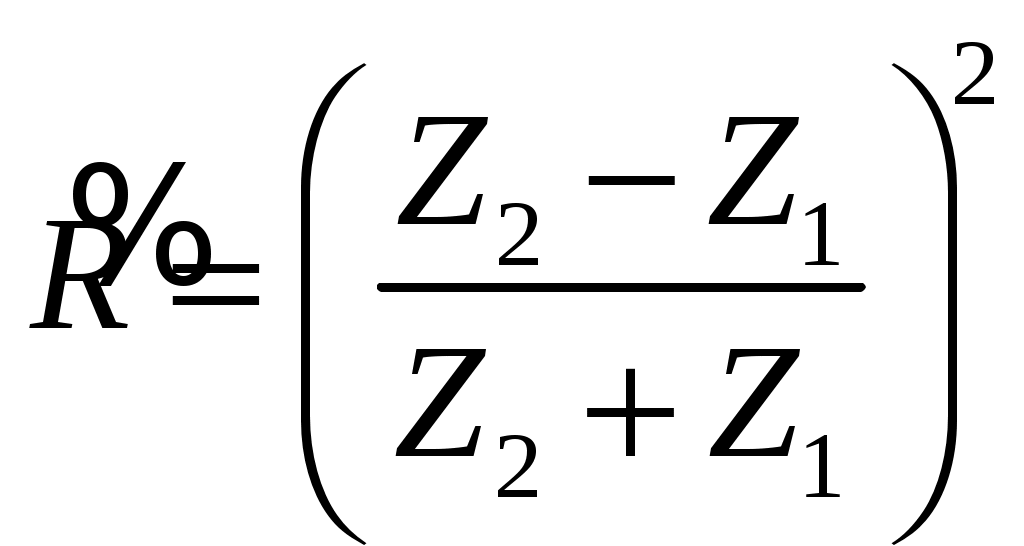 (11) (11)
С учетом этого легко проверить соблюдение закона сохранения энергии
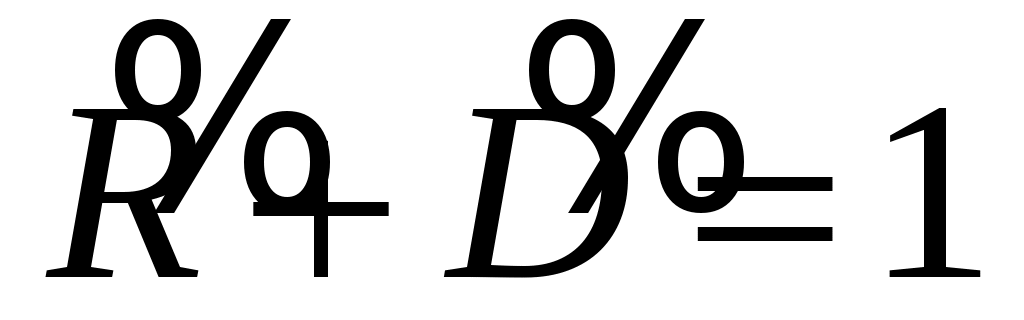 (12) (12)
Рассмотрим случай, когда скорость звука в нижней среде больше, чем в верхней (см. рис. 1.11). Мы знаем, что с увеличением угла волна в нижней среде быстро приближается к границе и при  сольется с ней. Значение сольется с ней. Значение 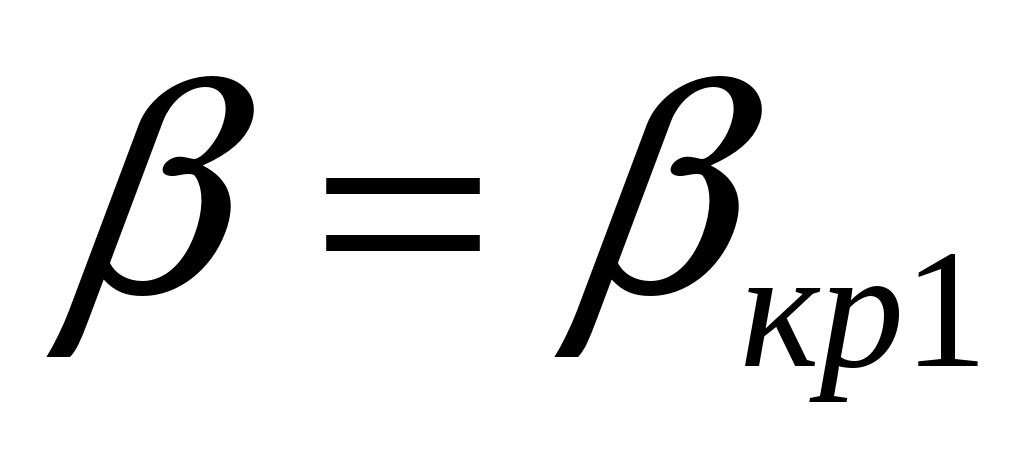 называют критическим. Если называют критическим. Если 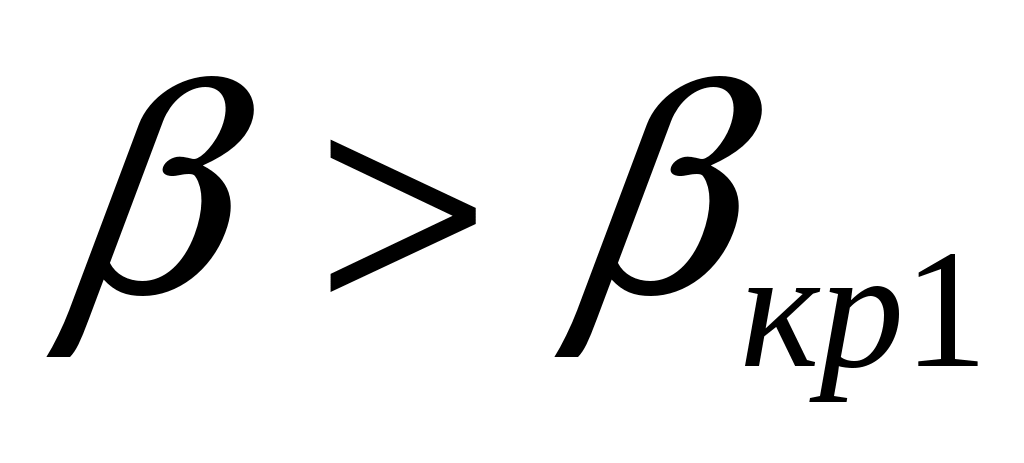 , то , то 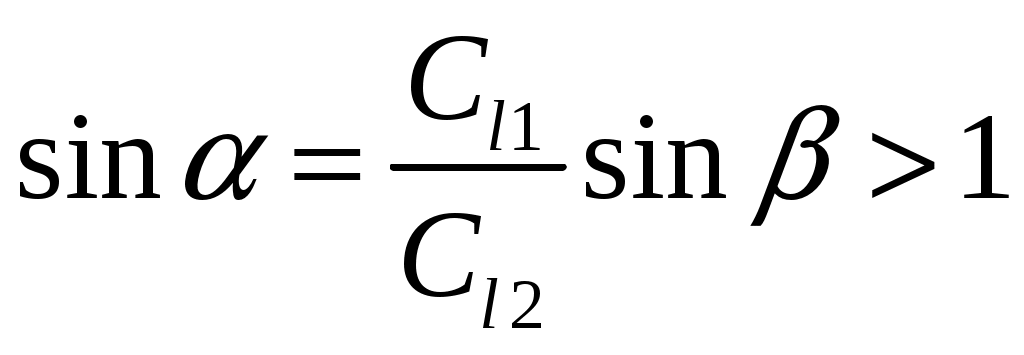 . Это вполне допустимо с точки зрения теории комплексных чисел . Это вполне допустимо с точки зрения теории комплексных чисел
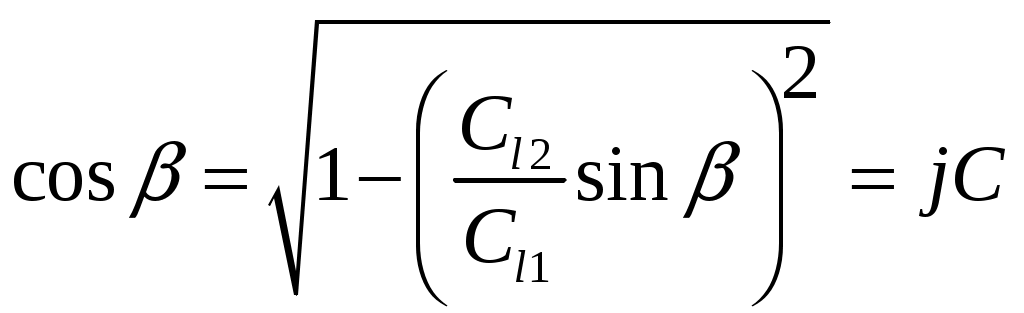 (13) (13)
В выражение для преломленной волны в этом случае войдет множитель 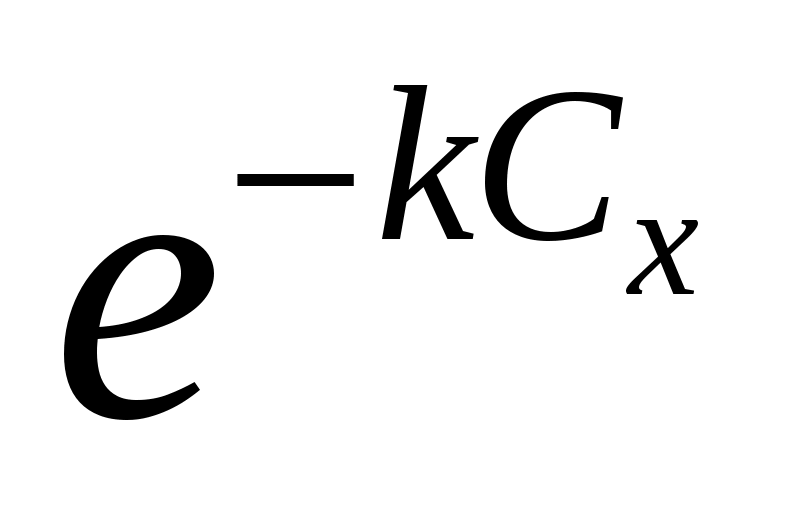 . Он показывает, что эта волна, распространяясь вдоль оси у, затухает с увеличением расстояния х от поверхности, причем тем быстрее, чем угол больше критического значения. Волна такого вида относится к типу неоднородных волн. Импеданс . Он показывает, что эта волна, распространяясь вдоль оси у, затухает с увеличением расстояния х от поверхности, причем тем быстрее, чем угол больше критического значения. Волна такого вида относится к типу неоднородных волн. Импеданс 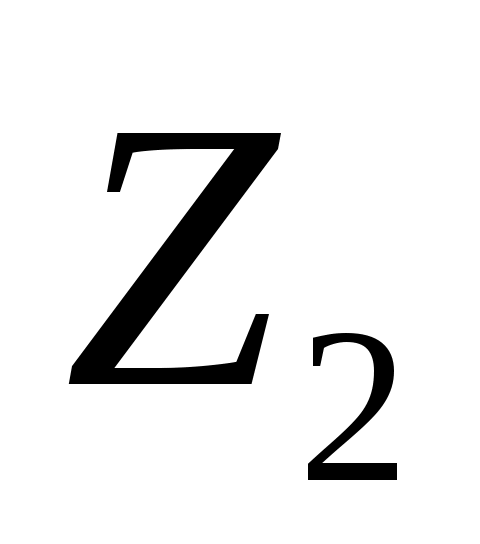 будет мнимым будет мнимым
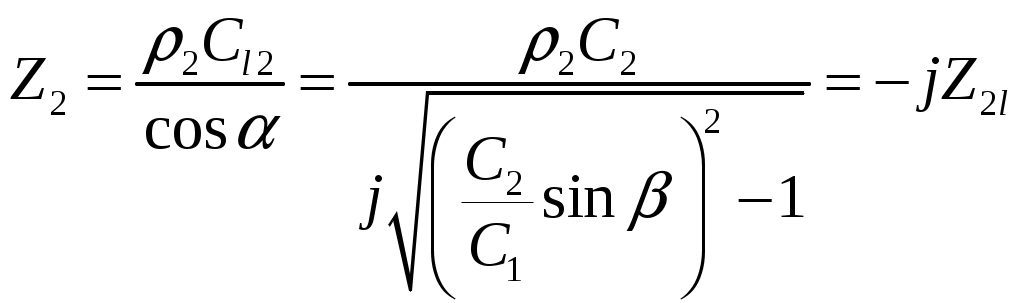 (14) (14)
Коэффициент отражения 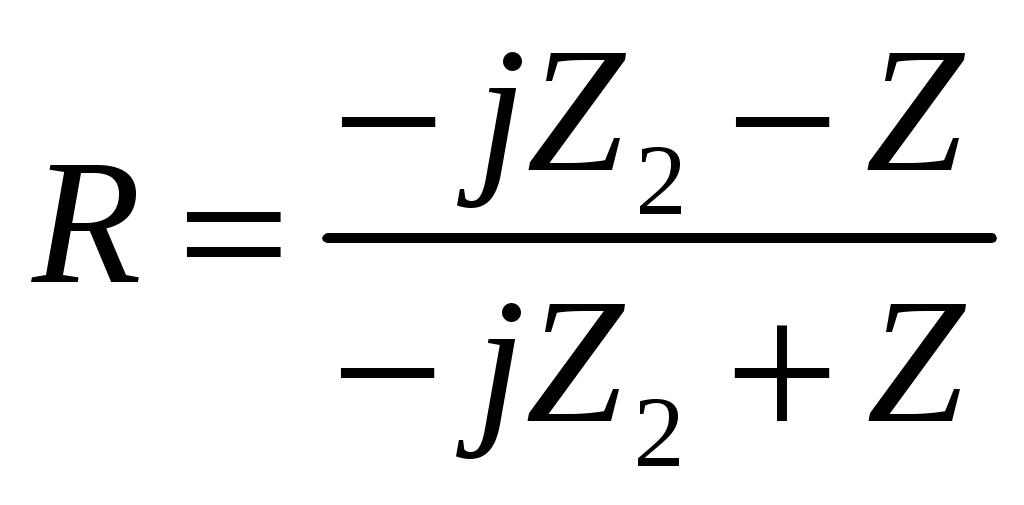 является комплексной величиной, причем R=1, т. е. отраженная волна имеет амплитуду, равную амплитуде падающей волны, но изменяет при отражении свою фазу. является комплексной величиной, причем R=1, т. е. отраженная волна имеет амплитуду, равную амплитуде падающей волны, но изменяет при отражении свою фазу.
Изменение этой фазы на величину, не кратную , при углах больше критического приводит к явлению незеркального отражения. Экспериментально установлено, что если на границу раздела сред падает ограниченная плоская волна под углом, несколько большим критического, то отраженный пучок лучей как бы смещается вдоль поверхности тела относительно падающего (рис. 9).
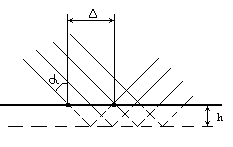
Рис. 9 Смещение пучка волн при незеркальном отражении
Смещение такое, как если бы отражение происходило зеркально от некоторой мнимой границы расположенной на некоторой глубине h под действительной поверхностью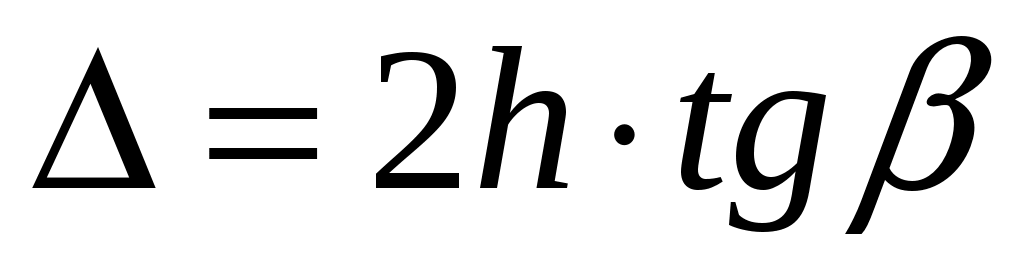 . Разность фаз волны, отразившейся от мнимой границы, т. е. прошедшей путь АED, и прямой волны, прошедшей путь АBС, равна . Разность фаз волны, отразившейся от мнимой границы, т. е. прошедшей путь АED, и прямой волны, прошедшей путь АBС, равна 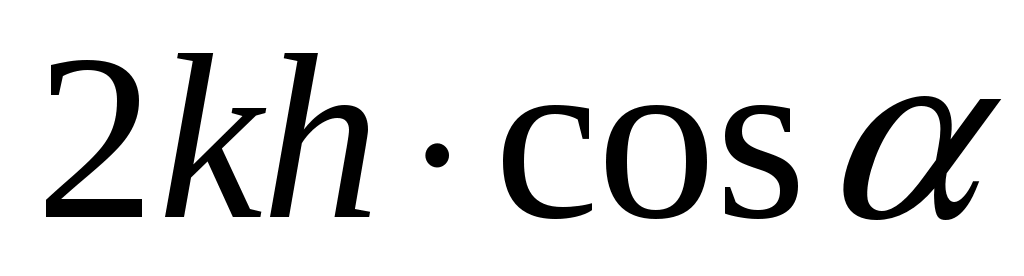 . Оказывается, что значение совпадает с изменением фазы коэффициента отражения. . Оказывается, что значение совпадает с изменением фазы коэффициента отражения.
Смещение пучка тем больше, чем ближе угол падения к критическому значению. Поэтому данное явление можно рассматривать как перенос энергии вдоль поверхности неоднородной волной. Чем ближе угол к критическому значению, тем больше амплитуда неоднородной волны на заданной глубине, тем больше расстояние она пробегает вдоль поверхности.
Если первой и второй средой являются твердые тела, то из закона синусов вытекает возможность существования целого ряда критических углов. Первый критический угол существует, когда падающая волна продольная и 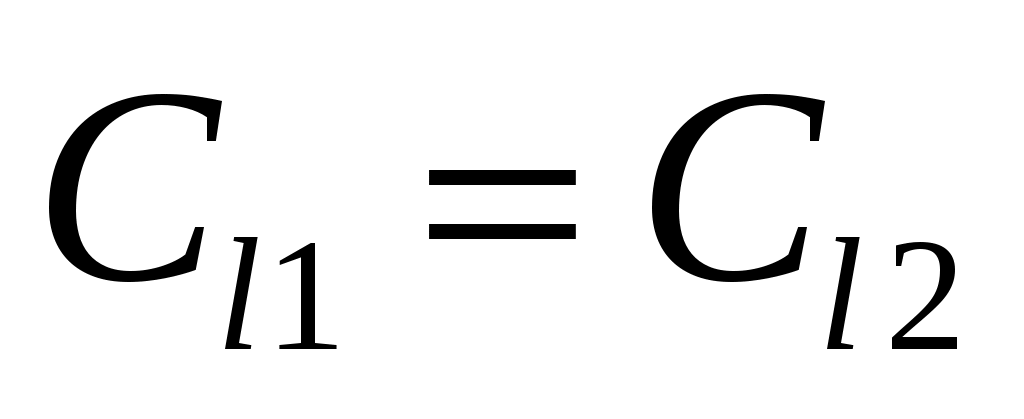 . Он соответствует условию слияния преломленной продольной волны с поверхностью, т. е. . Он соответствует условию слияния преломленной продольной волны с поверхностью, т. е.
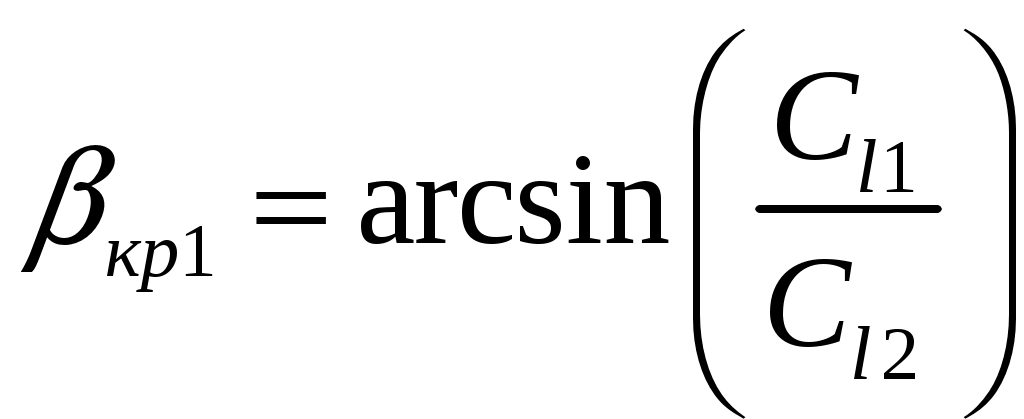 (15) (15)
Вдоль границы в этом случае распространяется неоднородная волна. Эту волну называют головной, используют для целей дефектоскопии. Если преобразователь соприкасается лишь с небольшим участком поверхности объекта контроля (изделия), а остальная часть его поверхности свободна, то головная волна должна обращаться в нуль на этой поверхности для выполнения граничных условий - напряжения на поверхности равны нулю. Под поверхностью объекта головная волна имеет максимальное значение напряжения. Это значение располагается на луче, составляющем угол 12 с поверхностью (для стали). Итак, с помощью головной волны можно обнаружить подповерхностные дефекты, при этом головная волна нечувствительна к неровностям объекта контроля.
Второй критический угол кр.2 существует, когда падает продольная волна и 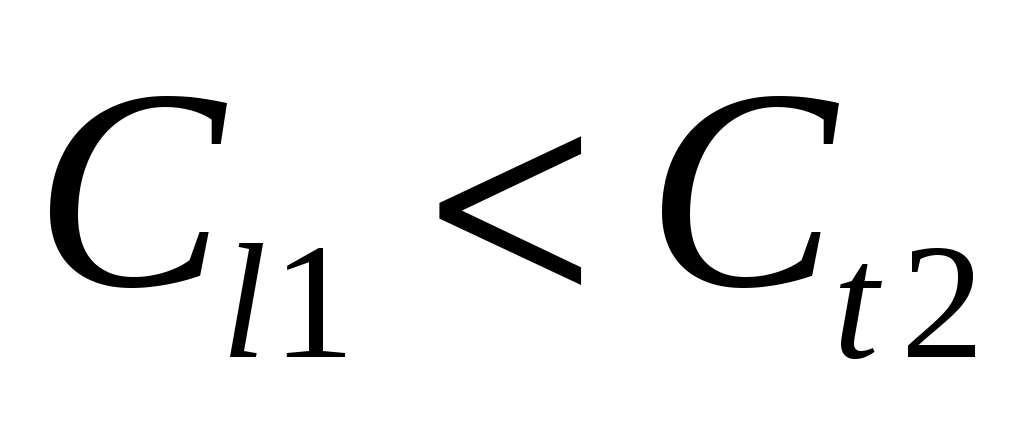 . Он соответствует условию слияния с поверхностью преломленной поперечной волны, т. е. . Он соответствует условию слияния с поверхностью преломленной поперечной волны, т. е.
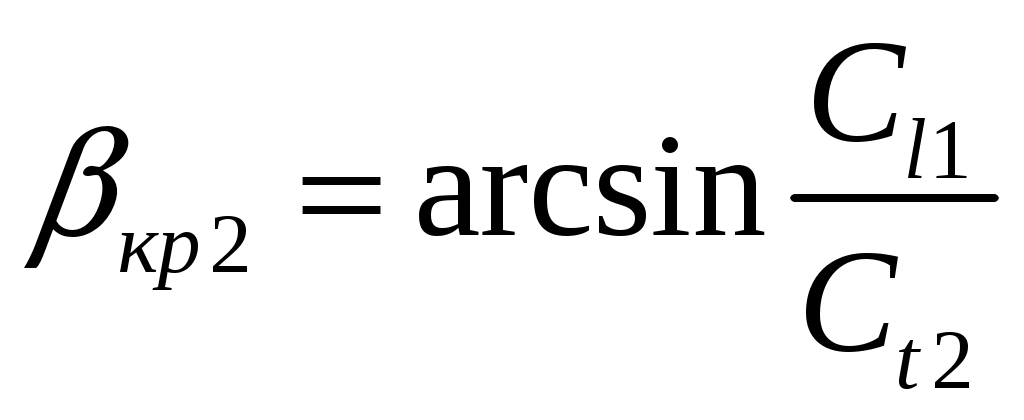 (16) (16)
Соответствующую неоднородную волну трудно отличить от поверхностной рэлеевской волны.
Третий критический угол кр3 существует при падении поперечной волны. Поскольку 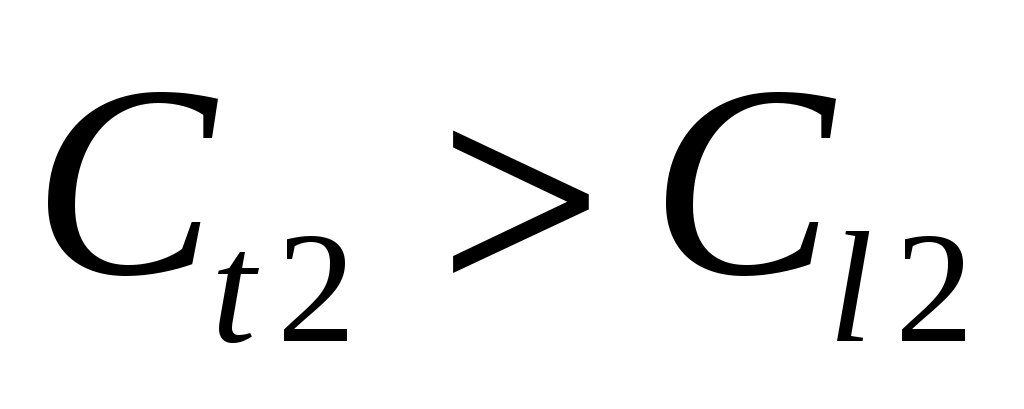 при при
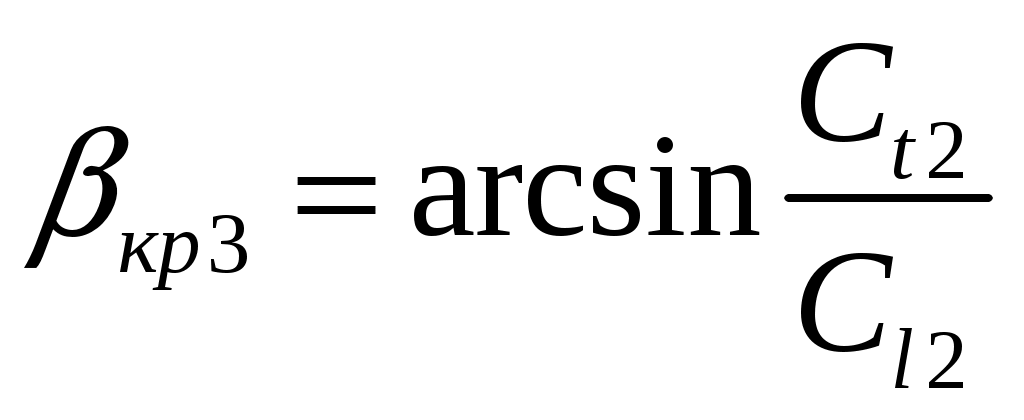 (17) (17)
продольная отраженная волна сольется с поверхностью и станет неоднородной.
Граничных условий всегда достаточно для определения амплитуд всех отраженных и преломленных волн. Например, на границе двух плотно соединенных твердых тел имеются четыре условия (равенство нормальных и тангенциальных смещений и напряжений по обе стороны от границы), позволяющих рассчитать четыре волны, показанные на рис. 1.11. На практике часто встречается случай двух твердых тел, разделенных очень тонким слоем жидкости. Слой считается настолько тонким, что изменением фазы волны при его прохождении можно пренебречь, однако наличие его приводит к появлению четырех других граничных условий: нормальные напряжения и смещения равны, а тангенциальные напряжения по обе стороны от границы обращаются в нуль.
Формулы для коэффициентов отражения и прозрачности для случая двух твердых тел или жидкости и твердого тела могут быть получены путем обобщения соотношений, выведенных ранее для границы двух жидкостей. Формулы (7) и (10) можно записать
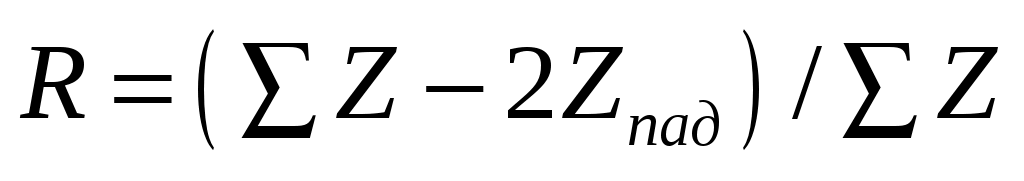 (18) (18)
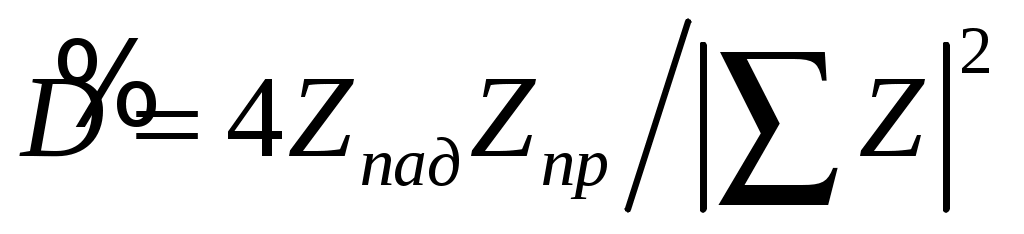 (20) (20)
где Z - сумма импедансов всех отраженных и преломленных волн;
Zпад - импеданс падающей волны;
Zпр - импеданс прошедшей волны.
В этом обобщенном виде формулы пригодны для случая, когда одна или обе среды - твердое тело, причем формулу (18) применяют для расчета отраженной волны, одинаковой по типу с падающей, а формулу (19) - для расчета всех коэффициентов прозрачности и коэффициента отражения для волны, не одинаковой по типу с падающей. Импедансы для продольной и поперечной волн в твердом теле имеют вид
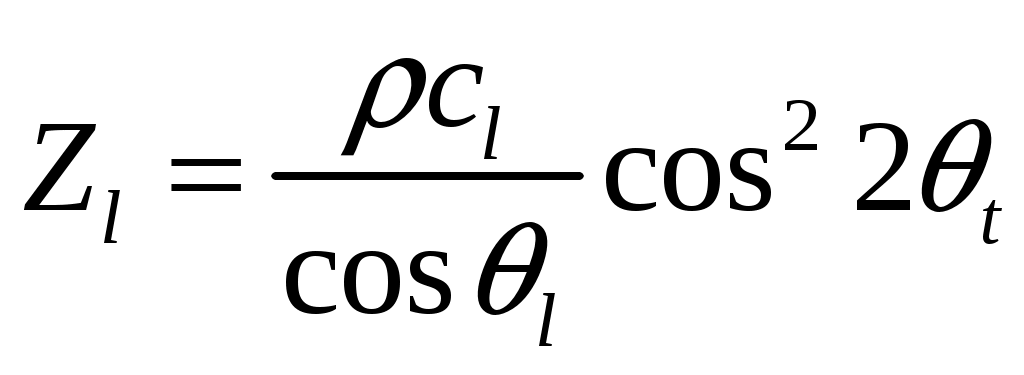 (21) (21)
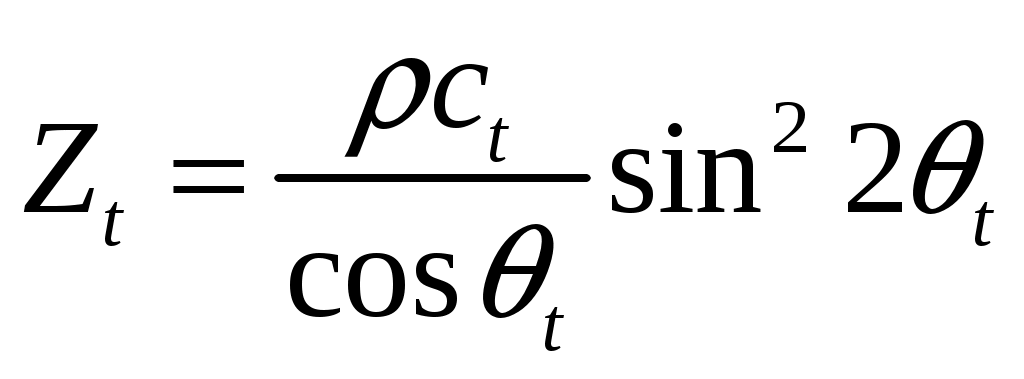 (22) (22)
гдеl и t - углы между направлением распространения соответствующих волн и нормалью к поверхности.
При углах, больших критического значения, соответствующие импедансы становятся мнимыми подобно (14).
На рис. 1.15 приведены зависимости коэффициентов прозрачности по энергии, рассчитанные для сред, весьма часто встречающихся в дефектоскопии оргстекло – масло – сталь.
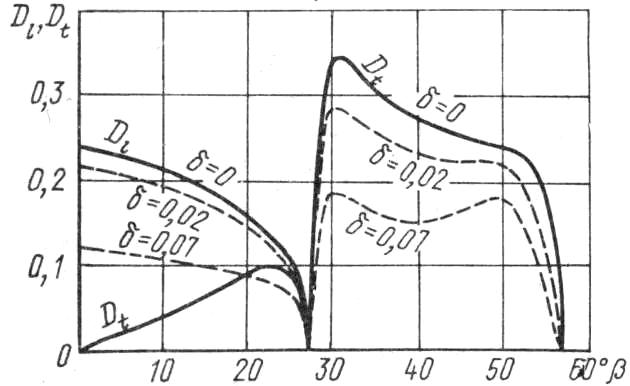
Рис. 10 Коэффициенты прозрачности для границы оргстекло - сталь
|
|
|
 Скачать 4.67 Mb.
Скачать 4.67 Mb.



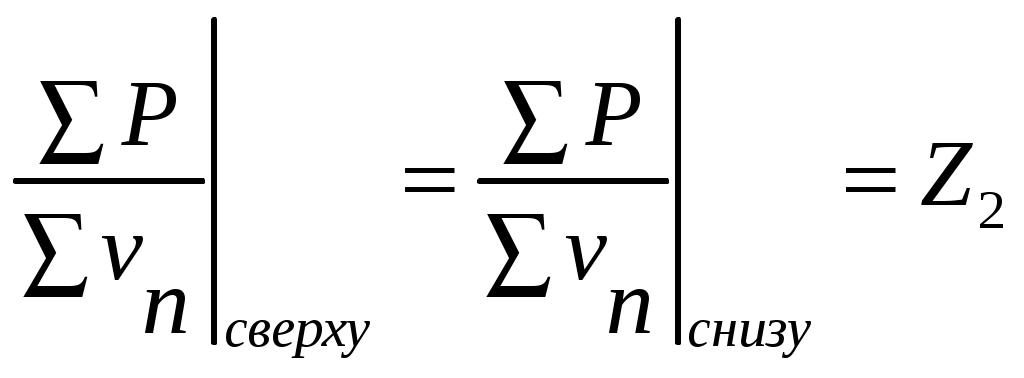 (5)
(5)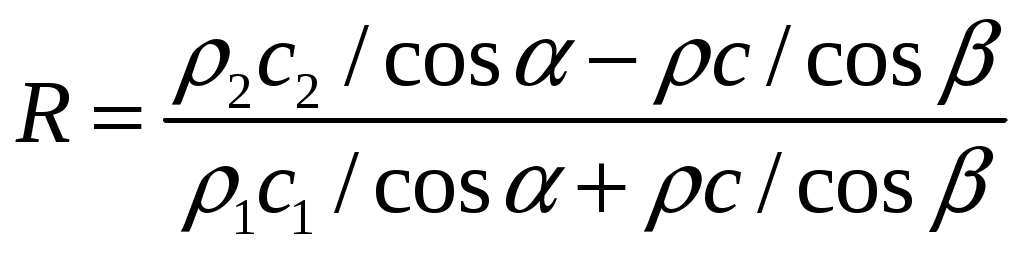 (8)
(8)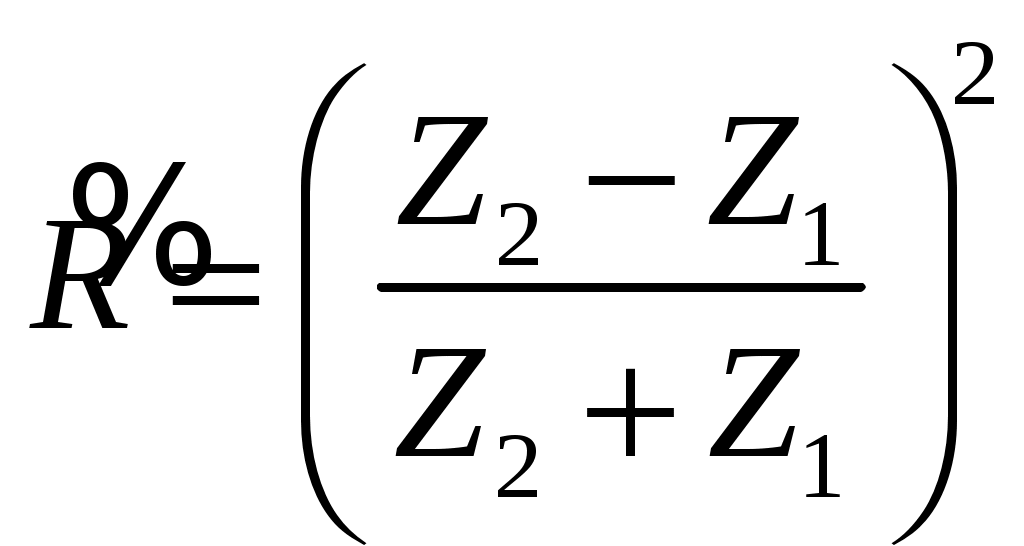 (11)
(11)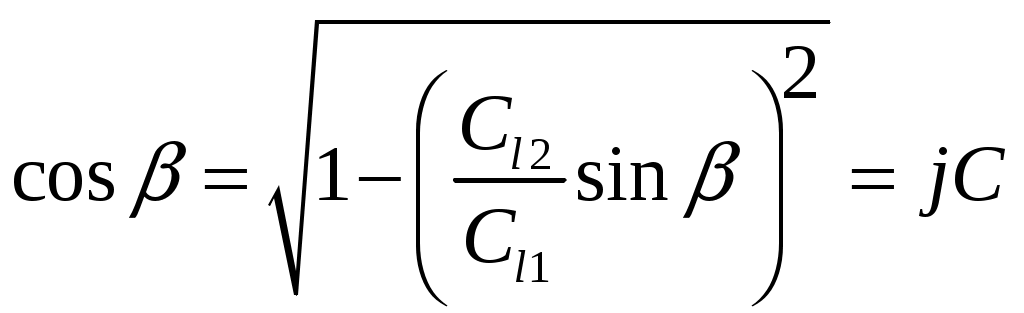 (13)
(13)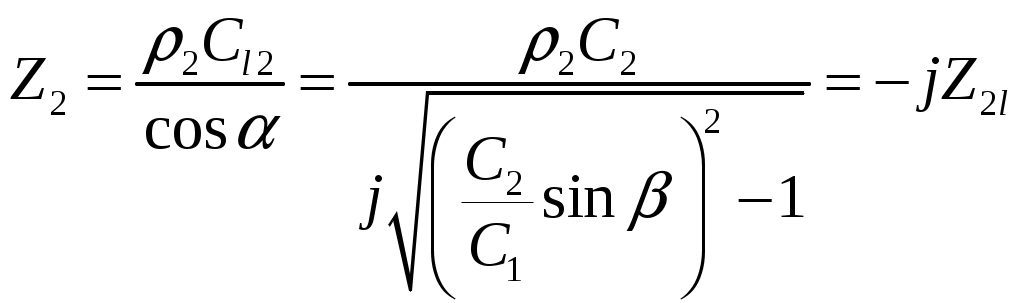 (14)
(14)
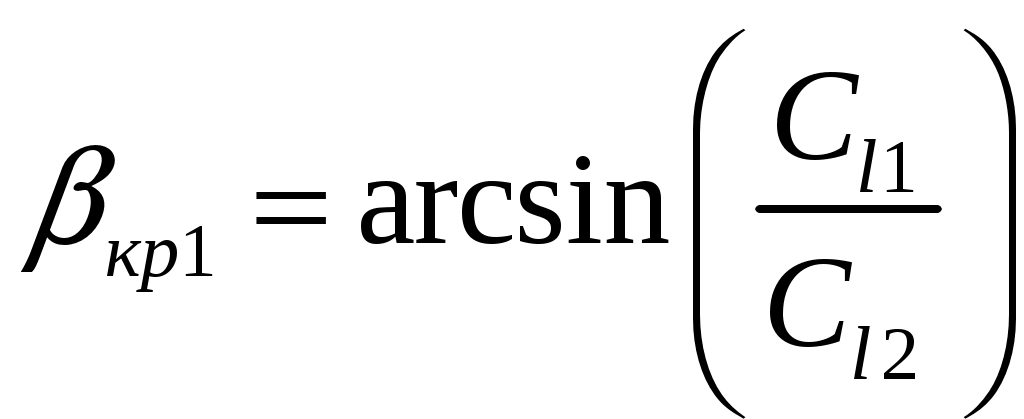 (15)
(15)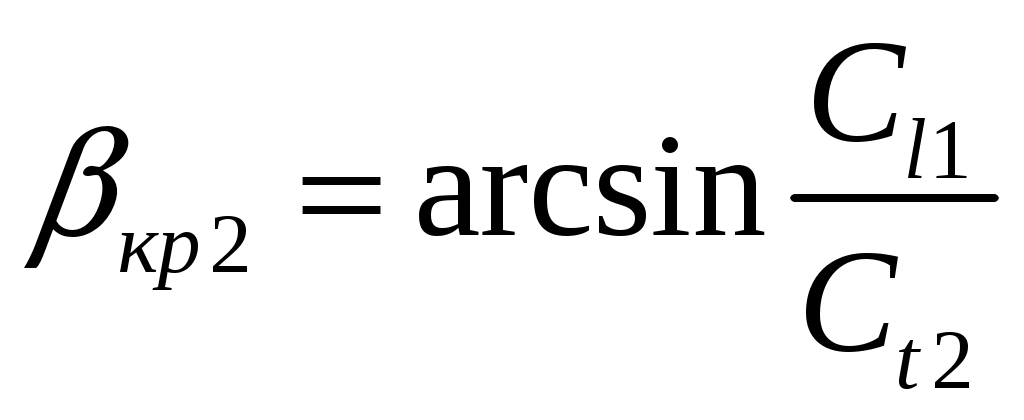 (16)
(16)